Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

208 4. Gauge Theories and Quantum-Chromodynamics
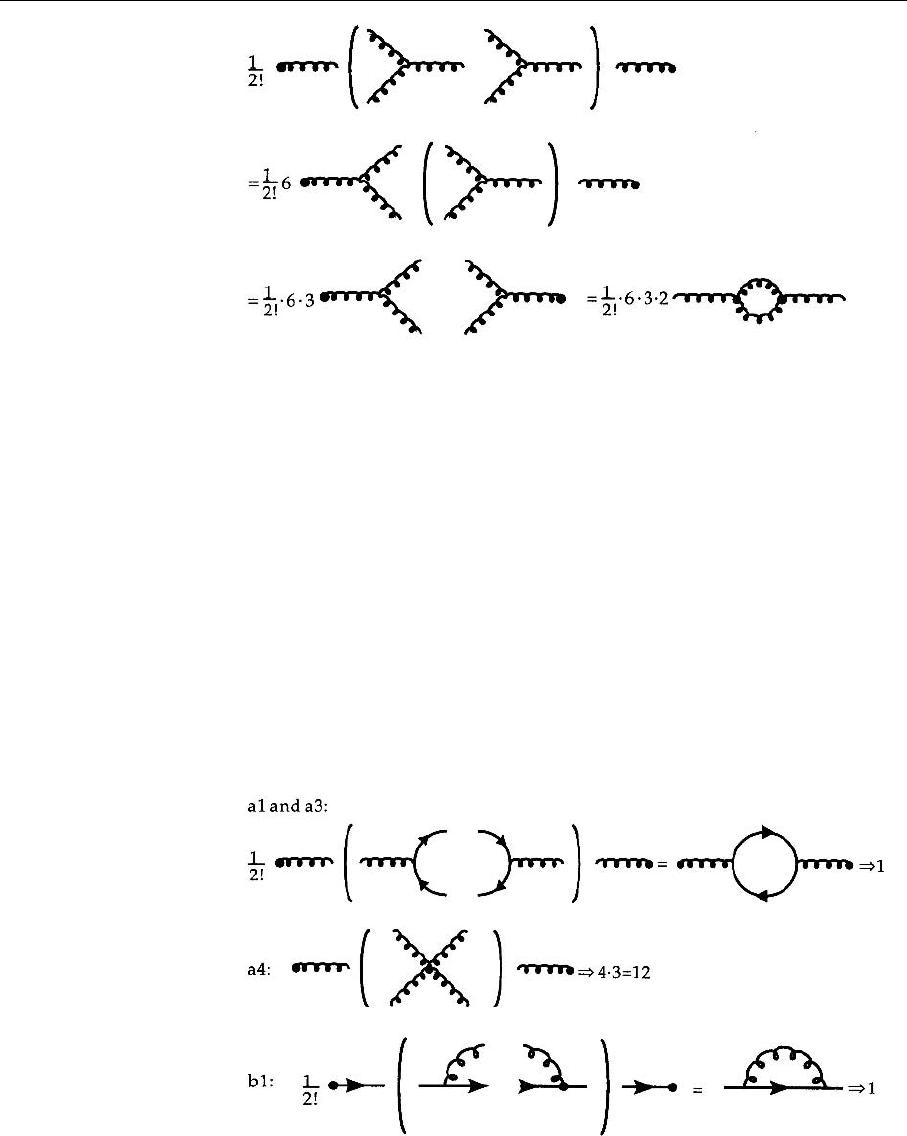
Fig. 4.19. The symmetry
factor for the graph in Fig.
4.18. We get from the first
to the second line a factor of
6 =3·2 since we have three
possibilities to connect the
left external gluon line with
one leg of the three gluon
vertices. From the second
to the third line we aquire
a factor of 3 due to the same
reasoning. The connection
of the two remaining three
gluon vertices again is pos-
sible in two different ways.
The factor 1/2! is due to the
fact that we are considering
second order in perturbation
theory
Fig. 4.20. The symmetry
factor for the other graphs in
Fig. 4.14
Fig. 4.21. The symmetry
factor for the second graph
in Fig. 4.15
As the two factors 6
2
= (3!)
2
are absorbed in the 2 ×6termsofthetwo
3-gluon vertices we are left with a factor 1/2. The corresponding factors for the
other graphs are derived in Fig. 4.20.
Following this scheme it is easy to obtain (see Figs. 4.20–4.24) any symmetry
factor of interest. The whole expression for Π
aa (a2)
µµ
is obviously very similar to
(4.106) except for the different nominator, which we simplify first using
f
abc
f
a
bc
= δ
aa
C
2
=δ
aa
N for SU(N ). (4.123)
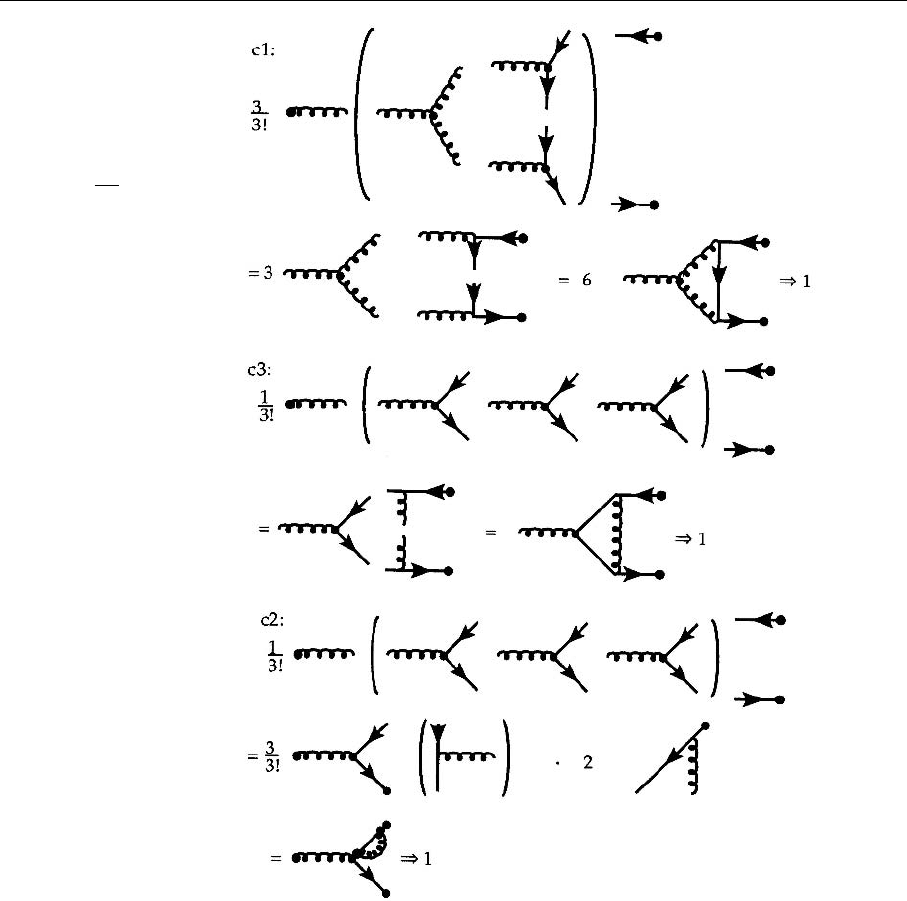
To obtain the symmetry factor for the second graph in Fig. 4.16 a general
remark will be helpful. To obtain symmetry factors for n-th order pertubation
theory we always have to deal with contributions like the one depicted below.
Very schematically we displayed the n-th order contribution that can occur in
QCD due to the 4 possible interaction vertices.
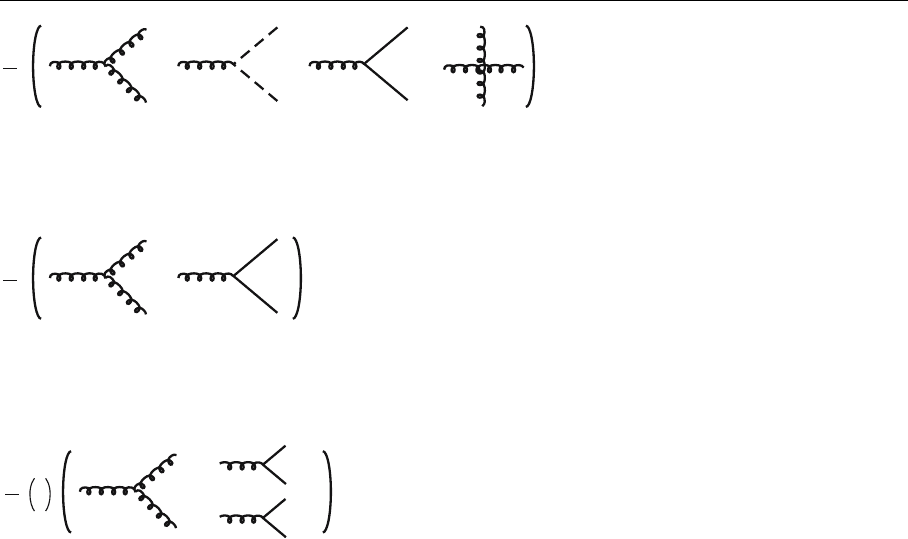
4.4 The Renormalized Coupling Constant of QCD 209
1
n!
++ +
n
Since we are interested in an interaction which includes 2 quark–quark–gluon
vertices and 1 3-gluon vertex we can restrict ourselves to
1
3!
+
3
Now we simply use the binomial expansion to glue the vertices together in such
a manner that we get the diagram of interest:
1
3!
3
2
Inserting the external lines, we thus proceed to Fig. 4.22.
We get back to the calculation of the graph (a2) in (4.122):
{...}
=3δ
aa
−g
µµ
(k −q)
2
+(k −q)
µ
(q +2k)
µ
−(k −q)
µ
(k +2q)
µ
−(q −k)
µ
(2k +q)
µ
−g
µµ
(q +2k)
2
+(2q +k)
µ
(q +2k)
µ
+(q −k)
µ
(2q +k)
µ
+(q +2k)
µ
(2q +k)
µ
−4(2q +k)
µ
(2q +k)
µ
=3δ
aa
−g
µµ
k
2
−2k ·q +q
2
+q
2
+4k ·q +4k
2
+k
µ
k
µ
(2 −1 +2 +2 −1 +2 −4)
+k
µ
q
µ
(−2−2 +1 +4 +1 +1 −8)
+q
µ
k
µ
(1 +1 −2 +1 −2 +4 −8)
+q
µ
q
µ
(−1+2 −1 +2 +2 +2 −16)
=3g
2
δ
aa
−g
µµ
2q
2
+2k ·q +5k
2
+2k
µ
k
µ
−5k
µ
q
µ
−5k
µ
q
µ
−10q
µ
q
µ
. (4.124)
210 4. Gauge Theories and Quantum-Chromodynamics
Fig. 4.22. The symme-
try factor for the second
graph in Fig. 4.16 (3rd-order
perturbation theory implies
1/3!binomial for the combi-
nation of one 3-gluon vertex
and two quark–gluon ver-
tices:
3
2
=
3!
2!1!
= 3)
Fig. 4.23. The symmetry
factor for the fourth graph in
Fig. 4.16
Fig. 4.24. The symmetry
factor for the third graph in
Fig. 4.16
We again substitute
q
µ
→q
µ
−k
µ
z (4.125)
and keep only the terms with even powers in q
µ
:
{...}⇒3δ
aa
−g
µµ
2q
2
+2k
2
z
2
−2k
2
z +5k
2
+2k
µ
k
µ
+5k
µ
k
µ
z +5k
µ
k
µ
z −10k
µ
k
µ
z
2
−10q
µ
q
µ

4.4 The Renormalized Coupling Constant of QCD 211
⇒3δ
aa
−g
µµ
−2k
2
z(1 −z) +5k
2
+2k
µ
k
µ
+10k
µ
k
µ
z(1 −z) −2g
µµ
q
2
−
5
2
g
µµ
q
2
=: 3δ
aa
A
µµ
+B
µµ
q
2
, (4.126)
defining A
µµ
and B
µµ
to abbreviate the corresponding terms. Repeating the
Feynman trick (4.108) for the propagator product ((q +k)
2
+iη)
−1
·(q
2
+iη)
−1
and introducing again Euclidean coordinates
˜
q
µ
=(iq
0
, q), the analogue to
(4.112) now becomes
Π
aa (a2)
µµ
(k) =
3
2
g
2
δ
aa
i
1
0
dz
∞
0
d
d
˜
q
(2π)
4
µ
4−d
−B
µµ
˜
q
2
+ A
µµ
[
˜
q
2
−k
2
z(1 −z) −iη]
2
=
3
2
g
2
δ
aa
i
1
0
dz
µ
4−d
π
d
2
(2π)
4
1
ε
A
µµ
+2B
µµ
k
2
z(1 −z)
×
−k
2
z(1 −z)
−ε
+O(ε) . (4.127)
In the last step we have directly inserted the analogue expression from (4.119).
The z integral now becomes
g
µµ
2k
2
+
9
2
k
2
2
1
0
dz
[
z(1 −z)
]
1−ε
−5g
µµ
k
2
1
0
dz
[
z(1 −z)
]
−ε
+2k
µ
k
µ
1
0
dz
[
z(1 −z)
]
−ε
+10k
µ
k
µ
1
0
dz
[
z(1 −z)
]
1−ε
=
11
6
g
µµ
k
2
−5g
µµ
k
2
+2k
µ
k
µ
+10k
µ
k
µ
1
6
+O(ε)
=−
19
6
g
µµ
k
2
+
22
6
k
µ
k
µ
+O(ε) , (4.128)
where we have used (4.118) and
+
1
0
dz [z(1−z)]
−ε
= Γ(1 −ε)Γ(1 −ε)/
Γ(2 −2ε). This integral is a special case of the more general one
12
B(x, y) =
+
1
0
dzz
x−1
(1 −z)
y−1
=Γ(x)Γ(y)/Γ(x +y). Thus, all together we get
Π
aa (a2)
µµ
(k) =
3ig
2
δ
aa
(16π)
2
1
12
1
ε
−ln
−k
2
µ
2
+const
−19g
µµ
k
2
+22k
µ
k
µ
. (4.129)
12
See A.J.G. Hey and R.L. Kelly: Phys. Rep. 96, 72 (1983).

212 4. Gauge Theories and Quantum-Chromodynamics
k q,b+
ka
ka
'
m
m
'
q,c
Fig. 4.25. The chosen vari-
ables for the ghost loop con-
tribution to vacuum polar-
ization. b and c describe the
colour of the ghosts
This expression is not gauge invariant ( k
µ
Π
(a2)
µµ
= 0), which is quite reasonable,
since, as explained in Examples 4.2 and 4.3, gauge invariance is only restored by
including the ghost terms. More precisely the ghost fields are constructed such
that they cancel the contribution from the unphysical degrees of freedom of the
gluon field. These unphysical degrees of freedom violate the gauge symmetry.
Graph (a3). To see how this happens we next calculate the ghost contribu-
tion,
Π
aa (a3)
µµ
(k) =−g
2
f
abc
f
a
cb
d
4
q
(2π)
4
q
µ
(k +q)
µ
[(q +k)
2
+iη](q
2
+iη)
. (4.130)
Note that the color indices at f
abc
and f
a
cb
are constructed according to the
order: gluon, outgoing ghost, incoming ghost (see Example 4.2, (21)). The dif-
ference in sign is due to the fact that the ghost fields anticommute. Using (4.123)
and repeating the introduction of a Feynman parameter (see (4.108)) and shifting
according to q
µ
→q
µ
−k
µ
z, we obtain
Π
aa (a3)
µµ
(k) = 3g
2
δ
aa
1
0
dz
d
4
q
(2π)
4
1
4
g
µµ
q
2
−k
µ
k
µ
z(1 −z)
q
2
+k
2
z(1 −z) +iη
2
, (4.131)
where we also made use of q
µ
q
µ
=
1
4
g
µµ
q
2
according to (4.110) and dropped
all terms linear in q in the nominator. After introducing Euclidean coordinates
and translating (4.130) into a d-dimensional integral (as was done in the step of
passing from (4.111) to (4.112)), (4.130) becomes
Π
aa (a3)
µµ
(k) =
3g
2
δ
aa
i
16π
2
πµ
2
−k
2
ε
1
ε
+const
1
0
dz
−
2
4
g
µµ
k
2
−k
µ
k
µ
(1 −z)z
=
3g
2
δ
aa
i
16π
2
1
ε
−ln
−k
2
µ
2
+const
1
12
−g
µµ
k
2
−2k
µ
k
µ
. (4.132)
Together this gives
Π
aa (a2)
µµ
(k) +Π
aa (a3)
µµ
(k)
=
3g
2
δ
aa
i
16π
2
1
ε
−ln
−k
2
µ
2
+const
20
12
k
µ
k
µ
−g
µµ
k
2
. (4.133)
The sum of the gluon-plus-ghost vacuum graph is thus again gauge invariant.
This illustrates nicely the role of the ghost fields, namely to subtract out the un-
physical components of the A
µ
field, which are fixed by the chosen gauge. The

4.4 The Renormalized Coupling Constant of QCD 213
graph (a4) of Fig. 4.14 gives no contribution. This is best seen from the defining
equation (4.78) for dimensional regularization:
d
d
q
1
q
2
= 0 .
The bubble is proportional to such a term because it does not depend on the ex-
ternal momentum. The sum of all graphs shown in Fig. 4.14 is needed in the
renormalization procedure following Fig. 4.29. We denote it here as
Π
(a1)
µν
(k) +Π
(a2)
µν
(k) +Π
(a3)
µν
(k) =
k
µ
k
ν
−k
2
g
µν
Z
a
,
where the divergent factor
Z
a
= Z
(a1)
+Z
(a2)
+Z
(a3)
=
g
2
16π
2
1
ε
−ln
−k
2
µ
2
20
12
C
2
−
2
3
N
f
will be needed in the renormalization procedure following Fig. 4.29 below. The
factor C
2
will be discussed below, after (4.137).
Graph (b1). Next we calculate the self-energy graph
Σ
b
(k) = g
2
d
4
q
(2π)
4
γ
µ
q/
q
2
+iη
γ
µ
1
(q +k)
2
+iη
tr
λ
a
2
λ
a
2
1
3
. (4.134)
In this case we have to average over three quark colors, which leads to
the factor 1/3. Making use of γ
µ
q/γ
µ
= γ
µ
q
ν
γ
ν
γ
µ
=q
ν
γ
µ
(2g
µν
−γ
µ
γ
ν
) =
2q/ −γ
µ
γ
µ
q/ = 2q/ −4q/ =−2q/,wehave
Σ
b
(k) =
−2
3
4g
2
d
4
q
(2π)
4
q/
[(q +k)
2
+iη][q
2
+iη]
. (4.135)
Following the same steps as before gives
Σ
b
(k) =−
8
3
g
2
i
16π
2
1
ε
−ln
−k
2
µ
2
+const
(−k/)
1
0
dzz
=
4
3
g
2
i
16π
2
1
ε
−ln
−k
2
µ
2
+const
k/
≡ ik/Z
b
. (4.136)
The latter expression defines the divergent factor Z
b
, which will be important in
the renormalization procedure below (see Fig. 4.29 and (4.140)).
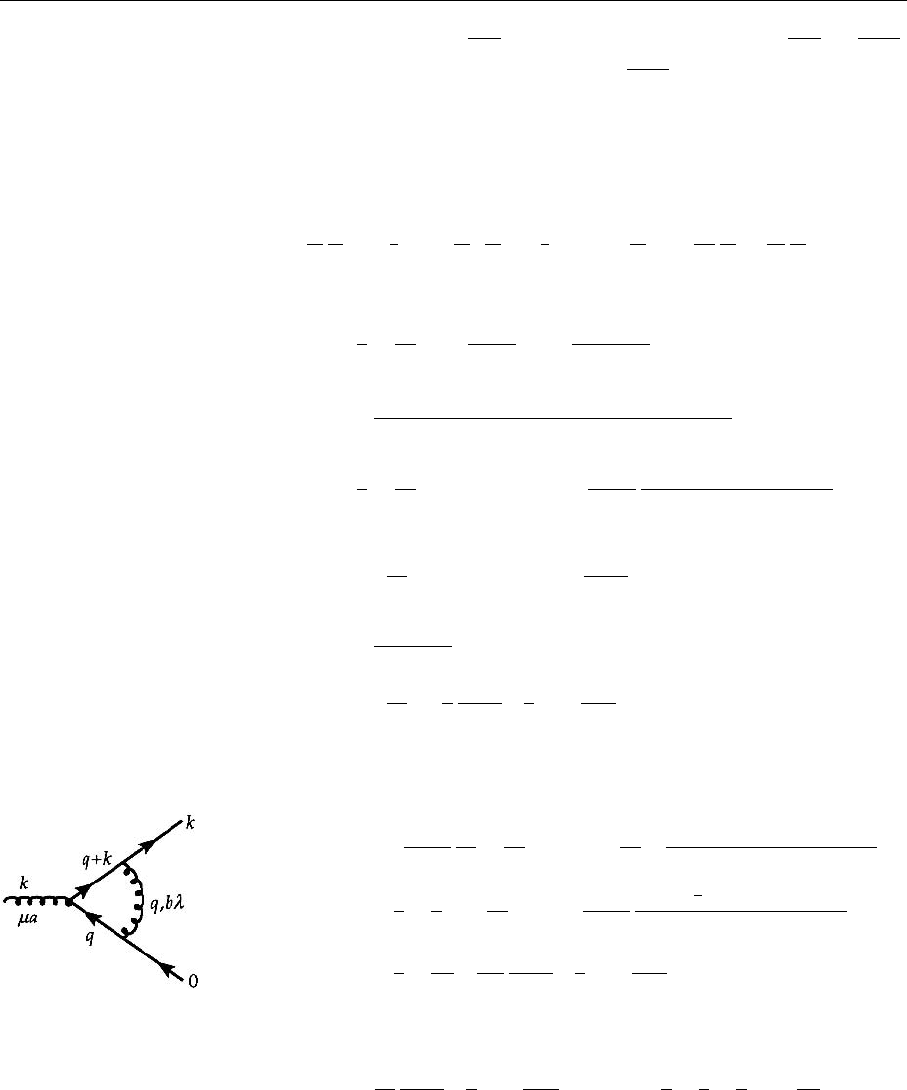
Graph (c1). We turn now to the vertex corrections Γ
a
µ
; see Fig. 4.27 and
(19) of Example 4.2. Γ
a
µ
is defined as Λ
a
µ
= γ
µ
λ
a
/2 +Γ
a
µ
(Γ
a
µ
corrects the bare
vertex γ
µ
λ
a
/2):
Γ
a (c1)
µ
=−ig
3
d
4
q
(2π)
4
f
abc
g
µλ
(k −q)
ν
+g
νµ
(−q −2k)
λ
+g
λν
(2q +k)
µ
×
λ
b
2
λ
c
2
γ
ν
q/γ
λ
(q
2
+iη)
2
(q +k)
2
+iη
. (4.137)
Fig. 4.26. The chosen vari-
ables for the self-energy
graph
Fig. 4.27. The chosen vari-
ables for the first vertex cor-
rection graph. The assign-
ment of momenta k and 0
for the outgoing quark lines
corresponds to the special
Lorentz system as explained
in the text
214 4. Gauge Theories and Quantum-Chromodynamics
Fig. 4.28. The chosen vari-
ables for the second vertex
correction graph
Here the quark propagator
1
q/+m
was taken in the limit m → 0, i.e.
1
q/+m
→
q/
q
2
+iη
.
This, together with the one-gluon propagator
1
q
2
+iη
, yields the above result.
To make things easy we choose a very special kinematics: we choose the
outgoing quark to have zero momentum. Or, in other words, we calculate in
a specific Lorentz frame where this is the case, relying on the fact that the diver-
gencies and thus the renormalization constants for coupling constants, masses,
and wave functions are Lorentz invariant. The divergent term is not affected
by this; only the finite ones are, and this makes things much easier. Using
−i f
abc
λ
b
2
λ
c
2
=−
i
2
f
abc
λ
b
2
,
λ
c
2
=
1
2
f
abc
f
dbc
λ
d
2
= N
δ
ad
2
λ
d
2
≡
C
2
2
λ
a
2
,wherewe
have utilized (4.123), we get
Γ
a (c1)
µ
=
1
2
C
2
λ
a
2
g
3
d
4
q
(2π)
4
1
0
dz
Γ(3)
Γ(2)Γ(1)
(1 −z)
×
(k/q/ −q
2
)γ
µ
−γ
µ
(q
2
+2k/q/) −2q/(2q +k)
µ
(q
2
+2qkz +k
2
z +iη)
3
=
1
2
C
2
λ
a
2
2g
3
1
0
dz (1 −z)
d
4
q
(2π)
4
−2q
2
γ
µ
−q
2
γ
µ
+...
(q
2
+k
2
z(1 −z) +iη)
3
= iC
2
λ
a
2
g
3
(+3)
1
0
dz (1 −z)
µ
4−d
16π
2
γ
µ
π
ε
−k
2
z(1 −z)
−ε
×
Γ(3)Γ(ε)
Γ(2)Γ(3)
+...
= iC
2
λ
a
2
3g
3
1
2
γ
µ
16π
2
1
ε
−ln
−k
2
µ
2
+...
. (4.138)
Graph (c3). Adopting again the same kinematics as for the calculation of
Γ
a (c1)
µ
(see Fig. 4.27), the second vertex graph Fig. 4.28 is
Γ
a (c
3
)
µ
= g
3
d
4
q
(2π)
4
λ
b
2
γ
λ
λ
a
2
(q/ +k/)γ
µ
q/
λ
b
2
γ
λ
1
(q
2
+iη)
2
(q +k)
2
+iη
= g
3
4
3
−
1
2
C
2
λ
a
2
(−2)
d
4
q
(2π)
4
1
4
(−2)γ
µ
q
2
(q
2
+iη)
2
(q +k)
2
+iη
= g
3
4
3
−
C
2
2
iλ
a
2
γ
µ
16π
2
1
ε
−ln
−k
2
µ
2
+...
.
All third-order vertex correction graphs (C1) and (C2) together add up to
Γ
a (c)
µ
= g
3
i
λ
a
2
γ
µ
16π
2
1
ε
−ln
−k
2
µ
2
+...
−
8
3
+
4
3
+
3
2
C
2
−
C
2
2
4.4 The Renormalized Coupling Constant of QCD 215
= g
3
i
λ
a
2
γ
µ
16π
2
1
ε
−ln
−k
2
µ
2
+...
C
2
−
4
3
≡ ig
λ
a
2
γ
µ
Z
c
. (4.139)
The divergent factor Z
c
defined in the last step will become important in the
renormalization procedure below.
Now we can renormalize the coupling constant. The way in which the vari-
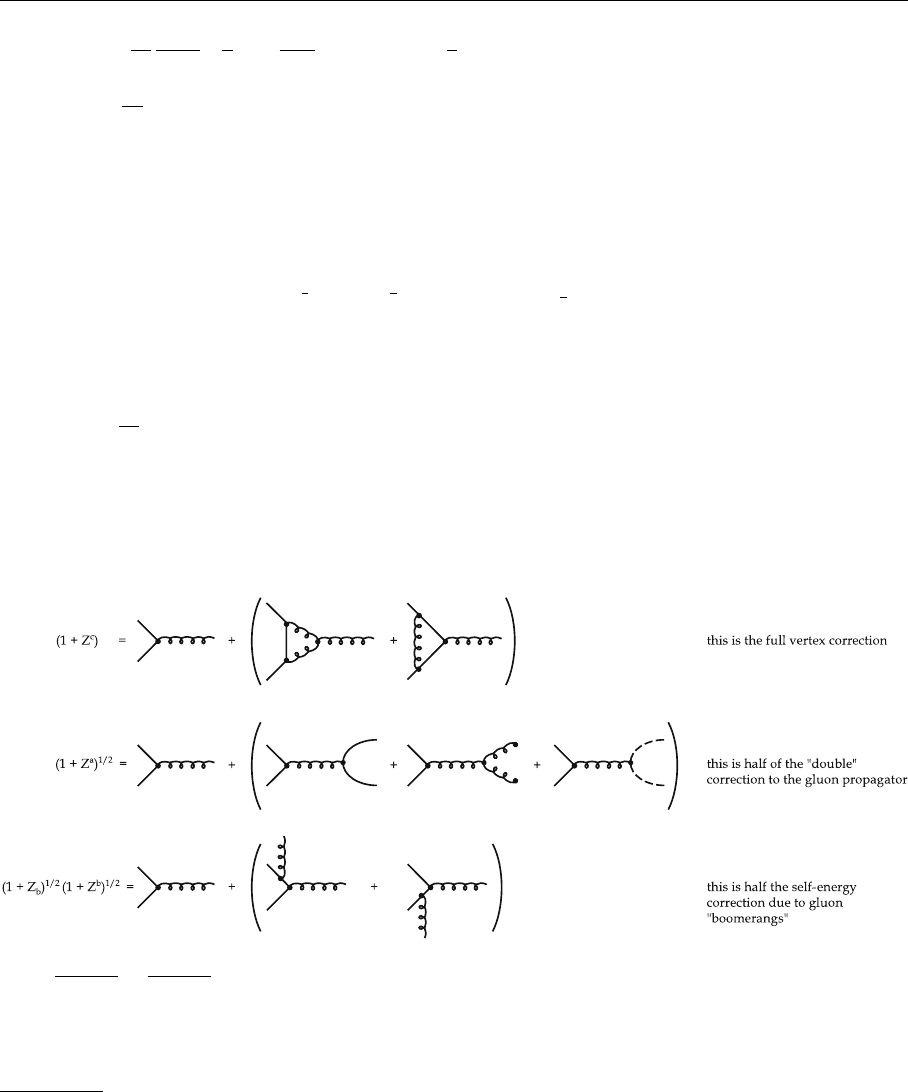
ous contributions combine is shown in Fig. 4.29. The renormalization procedure
is in fact rather easy. The square root of the vacuum polarization factor and the
self-energy factor multiply each of the respective lines. Thus the quark–gluon
vertex acquires the factors
1 + Z
b
1
2
1 + Z
b
1
2
(
1 + Z
c
)
1
(
1 + Z
a
)
1
2
. Note, that
this convention differs from the one used in QED,
13
where the renormalization
constants
˜
Z are related to the one used here by
˜
Z = 1 +Z. Recall that we defined
the renormalization constants as (see (4.113), (4.116), (4.120))
Γ
a(c)
µ
=ig
λ
a
2
γ
µ
Z
(c)
,Σ
(b)
= iγ
µ
k
µ
Z
b
,Π
(a)
µµ
i(k
µ
k
µ
−g
µµ
) Z
a
.
(4.140)
The renormalized quark–gluon vertex requires the full vertex correction Z
(c)
,
half of the correction to the gluon propagator and two times half of the correc-
tions from the self-energy. Graphically we can depict that as follows:
The
√
(1 + Z) ·
√
(1 + Z) partiton of the Z factors over two vertices is illustrated
in Fig. 4.29 for quark–quark scattering with gluon exchange.
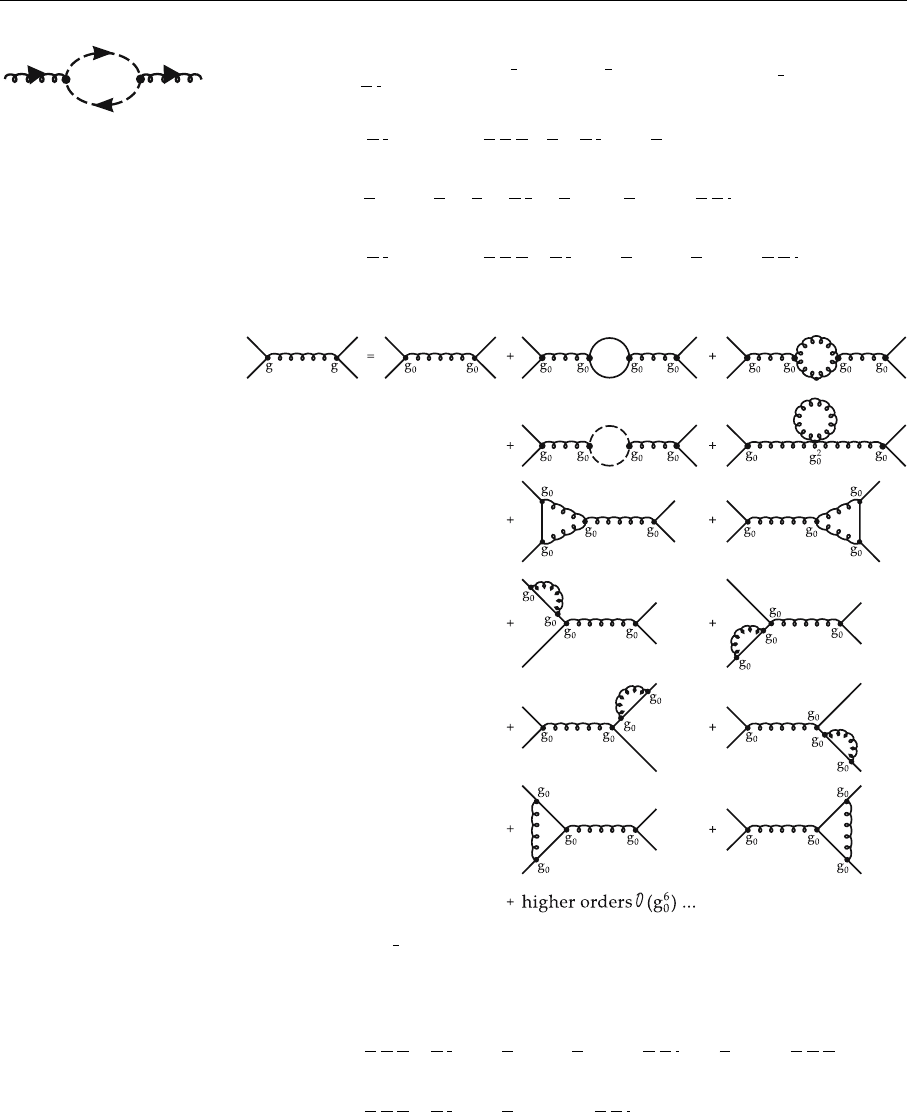
The full quark–quark scattering amplitude with its various contributions up
to O(g
6
0
) is shown in Fig. 4.30.
13
See W. Greiner and J. Reinhardt: Quantum Electrodynamics, 2nd. ed. (Springer,
Berlin, Heidelberg 1994).
216 4. Gauge Theories and Quantum-Chromodynamics
k q,b+
ka
ka
'
m
m
'
q,c
Fig. 4.29. The combination
of radiative corrections con-
tributing to the renormaliza-
tion of the coupling con-
stant g
Adding all contributions, the total vertex is given by
Γ
a(total)
µ
=−
λ
a
2
g
0
γ
µ
1 + Z
b
1
2
1 + Z
b
1
2
1 + Z
c
1
1 + Z
a
1
2
(4.141)
=−i
λ
a
2
g
0
γ
µ
#
1 −
g
2
16π
2
1
2
20
12
C
2
−
2
3
N
F
−
1
2
×2 ×
4
3
+
4
3
−
C
2
2
+
3
2
C
2
1
ε
−ln
−k
2
µ
2
+...
&
=−i
λ
a
2
g
0
γ
µ
#
1 −
g
2
16π
2
22
12
C
2
−
1
3
N
F
1
ε
−ln
−k
2
µ
2
+...
&
.
Fig. 4.30. Order g
6
0
correc-
tions to the quark–quark
scattering amplitude
Here
(
1 + Z
a
)
1
2
≈
(
1 +(1/2)Z
a
)
has been approximated. The renormalized
coupling constant is obtained from (4.141) by subtracting the value of the
correction at some renormalization scale M
2
:
g
R
= g
0
−
g
3
0
16π
2
11
6
C
2
−
1
3
N
F
1
ε
−ln
−k
2
µ
2
−
1
ε
+ln
−M
2
µ
2
= g
0
+
g
3
0
16π
2
11
6
C
2
−
1
3
N
F
ln
−k
2
M
2
. (4.142)

4.4 The Renormalized Coupling Constant of QCD 217
An important quantity in QCD is the so-called β function, which will be
discussed below (see, e.g. Exercise 5.11) The β function is defined as β =
M
(
∂g
R
/∂M
)
|
−k
2
=M
2
. It describes the dependence of the effective renormalized
coupling on the renormalization scale M
2
. It can now be easily calculated:
β = M
∂g
R
∂M
=−
g
3
0
16π
2
11
6
C
2
−
1
3
N
F
2M
M
2
M
=−
g
3
0
16π
2
11
3
C
2
−
2
3
N
F
+O(g
5
0
). (4.143)
This is the first term in the perturbative expansion for the β function. For QCD
we have to insert C
2
= 3. Let us reflect on the β-function issue in order to under-
stand the underlying ideas. Iteration and summation of the one-loop corrections
in terms of geometrical series leads to
g
2
(−k
2
) =
g
2
0
1 +
g
2
0
16π
2
11
3
C
2
−
2N
F
3
log
−k
2
M
2
(4.144)
where g
0
is the coupling constant defined at the scale M
2
. This is the famous
one-loop running coupling constant of QCD. Instead of doing this iteration and
resumming the one-loop corrections, one may follow a more formal approach,
as we will show now. As mentioned above, in QCD the so-called β function
allows a more general definition of the running coupling constant than just the
resummation method, based on perturbation theory. The β function is defined as
solution of the following differential equation
M
∂g
∂M
−k
2
=M
2
≡ β(g) =−b
0
g
3
+O(g
5
) (4.145)
and is determined order by order in perturbation theory. Above, in (4.143) and
(4.144), we have determined the coefficient b
0
entering on the right-hand side of
(4.146) as
b
0
=
1
16π
2
11
3
C
2
−
2N
F
3
. (4.146)
It is important to notice that (4.145) constitutes a differential equation for the
coupling constant g in its dependendce on the renormalization scale M, while
(4.146) is based on a resummation of one-loop diagrams. There will be situations
in which the function β(g) can be determined nonperturbatively. Then (4.145)
leads to more or less non perturbative expressions for the running coupling con-
stant. This remark may demonstrate the advantage of the β-function method for
the calculation of g(−k
2
). We follow this idea and solve the differential equa-
tion (4.145) to get an explicit solution for g(−k
2
) in the one-loop approximation.
Separation of the variables g and M yields
g(−k
2
)
g(M
2
)
dg
g
3
=−b
0
(−k
2
)
2
M
2
dM
M
(4.147)
