Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

238 4. Gauge Theories and Quantum-Chromodynamics

Returning to the standard normalization og the gluon ﬁeld we ﬁnally get

=−

bα

8π

+O(α

). (4.250)

4.5.7 Multiloop Corrections

Although in practical applications it is quite sufﬁcient to limit oneself to the

one-loop expressions for the anomalies (4.238) and (4.250), the question for

the higher order corrections still deserves a brief discussion. Until recently it

was generally believed that the question was totally solved. Namely, the axial

anomaly (by the Adler–Bardeen theorem) is purely one-loop while the scale

anomaly contains the complete QCD β-function in the right-hand side. In other

words, −bα

/8π in equation (4.250) is substitued by β(α

)/4π if higher order

corrections are taken into account.

Later it become clear, however, that the situation is far from being such simple

and calls for additional studies. Surprising though it is, the standard arguments

was ﬁrst revealed not within QCD but in a more complex model – supersym-

metric Yang–Mills theory. The minimal model of such a type includes gluons

and gluinos, which are Majorana fermions in the adjoint representation of the

colour group. The axial current and the dilatational current in supersymmetric

theories enter one supermultiplet and, consequently, the coefﬁcients in the chiral

and dilatation anomalies cannot be different – one-loop for ∂ · J

and multiloop

for ∂ · J

Being unable to discuss here the multiloop corrections in detail, we note only

that the generally accepted treatment is based on the confusion just mentioned in

the beginning of the last section. The standard derivation of the Adler–Bardeen

theorem seems to be valid only provided that the axial anomaly is treated as an

operator equality. At the same time the relation

β(α

)

4α



µν



ext

(4.251)

takes place only for the matrix elements.

It is quite natural to try to reduce both anomalies to a uniﬁed form, prefer-

ably to the operator form. Then ∂ · J

is exhausted by the one-loop approximation

(4.238), at least, within a certain ultraviolet regularization. As far as the trace

anomaly (scale anomaly) is concerned, in this case we do not know even the two-

loop coefﬁcient in front of the operator G

, to say nothing about higher-order

corrections.

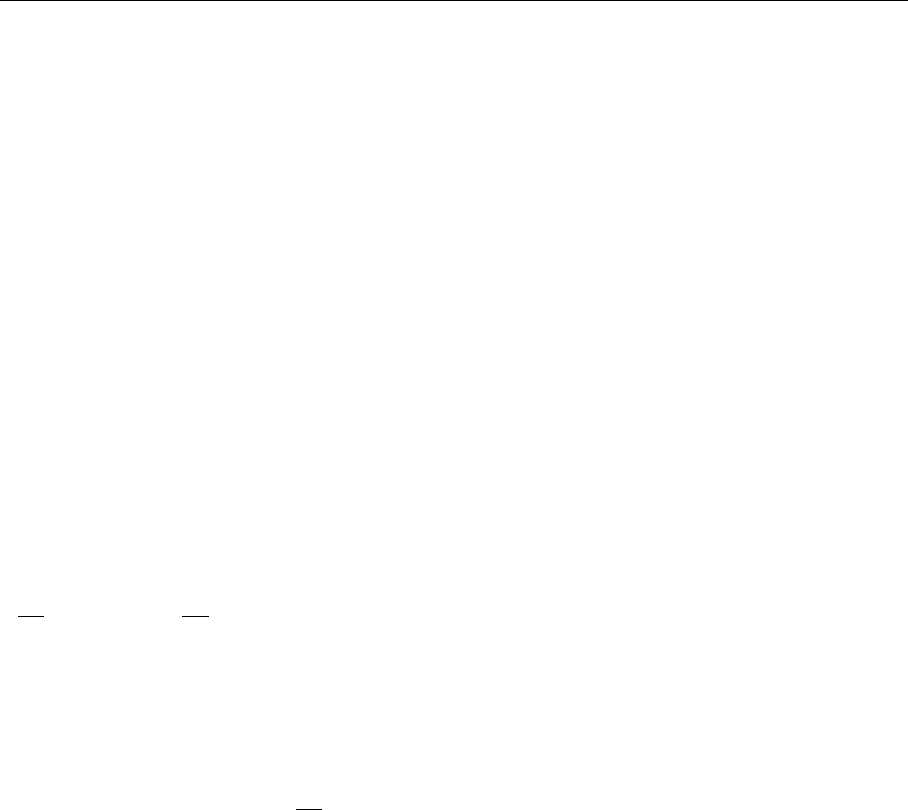
5. Perturbative QCD I: Deep Inelastic Scattering

In the last chapter we discussed how the QCD coupling constant depends on

the transferred momenta. Because of this speciﬁc dependence, QCD can only

be treated perturbatively in the case of large momentum transfers. For practi-

cal purposes, however, it is indispensable to know at what momentum values

the transition between perturbative and non-perturbative effects takes place. To

this end we again take a look at Fig. 1.1. The quark conﬁnement problem will be

considered later together with different models for its solution. A common fea-

ture of all these models is that they postulate nonperturbative effects. Since, for

example, the masses of the N resonances in Fig. 1.1 reach a value of 2.5GeV

and since on the other hand the rest masses of the constituent up and down

quarks are negligible, we can conclude that for momentum transfers less than

1 GeV, QCD is certainly still in the nonperturbative region. On the other hand,

Fig. 4.4 shows that even at momentum transfers of a few GeV, quarks inside

nucleons behave almost like free particles. Hence the transition from the nonper-

turbative to the perturbative region must take place quite rapidly, i.e., between

≈ 1GeVand

≈ 3 GeV. According to Fig. 4.8, QCD can only yield

such an immediate transition if the number of quark ﬂavors with masses less

than 1–2 GeV is not much larger than six. In fact there are only three or four

such quarks: up (m

=5.6 ±1.1MeV), down (m

= 9.9 ±1.1 MeV), strange

=199 ±33 MeV), and charm (m

= 1.35 ±0.05 GeV). The bottom quark is

with m

≈ 5 GeV too heavy, and so is the top quark, which was discovered at

the Fermilab Tevatron collider in 1995 and has a mass m

=174.3 ±5.1GeV.As

a further consequence of this sudden transition it is almost certain that for some-

what larger momentum transfers

all processes can be evaluated by means

of the usual perturbation theory, i.e., the QCD Feynman rules. It therefore seems

quite obvious to calculate QCD corrections to the parton model of deep inelastic

lepton–nucleon scattering. The next section treats these questions in some detail.

5.1 The Gribov–Lipatov–Altarelli–Parisi Equations

The Gribov–Lipatov–Altarelli–Parisi equations (GLAP) describe the inﬂuence

of the perturbative QCD corrections on the distribution functions that enter the

parton model of deep inelastic scattering processes. At this point we investigate

their structure and the functions that occur only for the two correction graphs in

240 5. Perturbative QCD I: Deep Inelastic Scattering

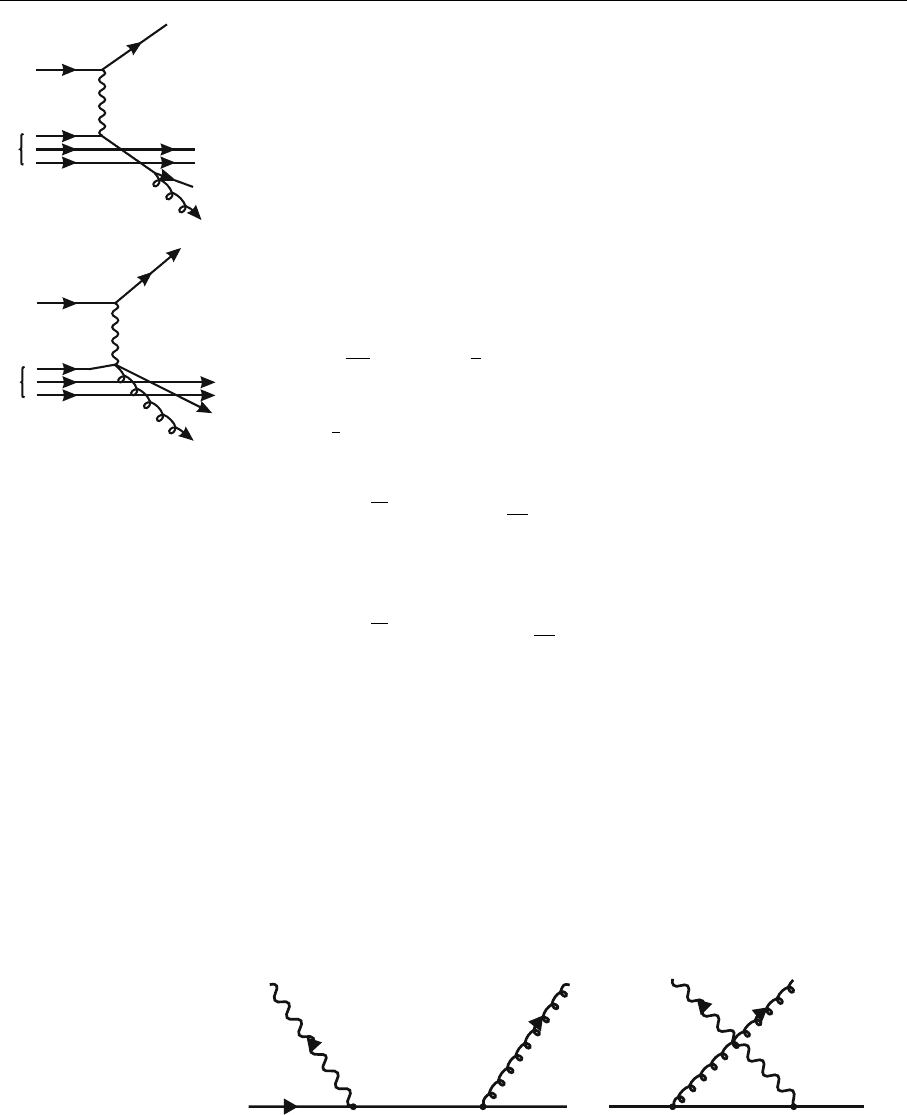
Fig. 5.1. Two correction

graphs for deep-inelastic

electron–nucleon scattering

q,m q,m

K, ,an K, ,an

p,i p,ip+q,i p+q-K,j p+q-K,jp-K,j

Fig. 5.2. Deﬁnition of the

quantities employed. p, q

and K stand for the cor-

responding four-momenta,

while i,µ, j,ν denote the

spin directions (polariza-

tions)

Fig. 5.1. In line with the parton-model assumptions, both the scattering parton

and the “emitted” gluon can be treated here as free particles. Having determined

the GLAP equations for the two graphs mentioned above it is quite easy to

extrapolate to their general form. We shall use the notation deﬁned in Fig. 5.2.

Obviously these graphs are similar to those for Compton scattering. Hence

their contribution to the scattering tensor W

µν

can be evaluated in analogy to the

corresponding QED graphs. The ﬁrst step towards this end is the determination

of the correct normalization factor. W

µν

is then just a factor entering the cross

section (see (3.22)); the photon progagator and the normalization factor of the

incoming photon have been separated. Bearing all these facts in mind one is led

to the correct result, which we want, however, to derive in a slightly different

way. We start with the scattering amplitude W

µµ



(3.33) – see also Example 3.2:

µµ



2π

x e

iqx



pol.

N|

(x)



(0)|N  . (5.1)

Note that



pol.

stands for the averaging over the incoming nucleon spin. In

order to obtain the contributions due to Fig. 5.2 we clearly have to insert

(x) =

Ψ(y)g



( y)γ



S( y −x)Q

Ψ(x) d

for the transition current operator

(x) and

(x) =

Ψ(x)Q

S(x −y)



Ψ(y) d

y (5.2)

as the exchange term.

Ψ and



denote the ﬁeld operators of a quark with ﬂa-

vor f and a gluon, respectively. Q

is the electric charge of the quark with ﬂavor f.

The space-time coordinate x characterizes the point of interaction between pho-

ton and current. The key observation for carrying out the calculation is that we

consider the quarks inside the nucleon as essentially free particles. Therefore,

instead of calculating the product of current operators

(x)

(0) in a hadronic

state N ||N  we adopt free quark states ψ ||ψ . This allows to calculate

the tensor W

µν

order by order perturbatively. The action of the operators

the quark states | ψ i.e.

| ψ implies that the operators

Ψ can be replaced by

5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 241

the quark wave functions ψ. Hence the above equations translate into

µµ



2π

x e

iqx



pol.



partons

(x)J



(0), (5.3)

(x) =

Ψ(y)gG



( y)γ



S( y −x)Q

Ψ(x) d

(x) =

Ψ(x)Q

S(x −y)



( y)γ



Ψ( y) d

y , (5.4)

The quark and gluon wave functions Ψ and G



will later on be taken as plane

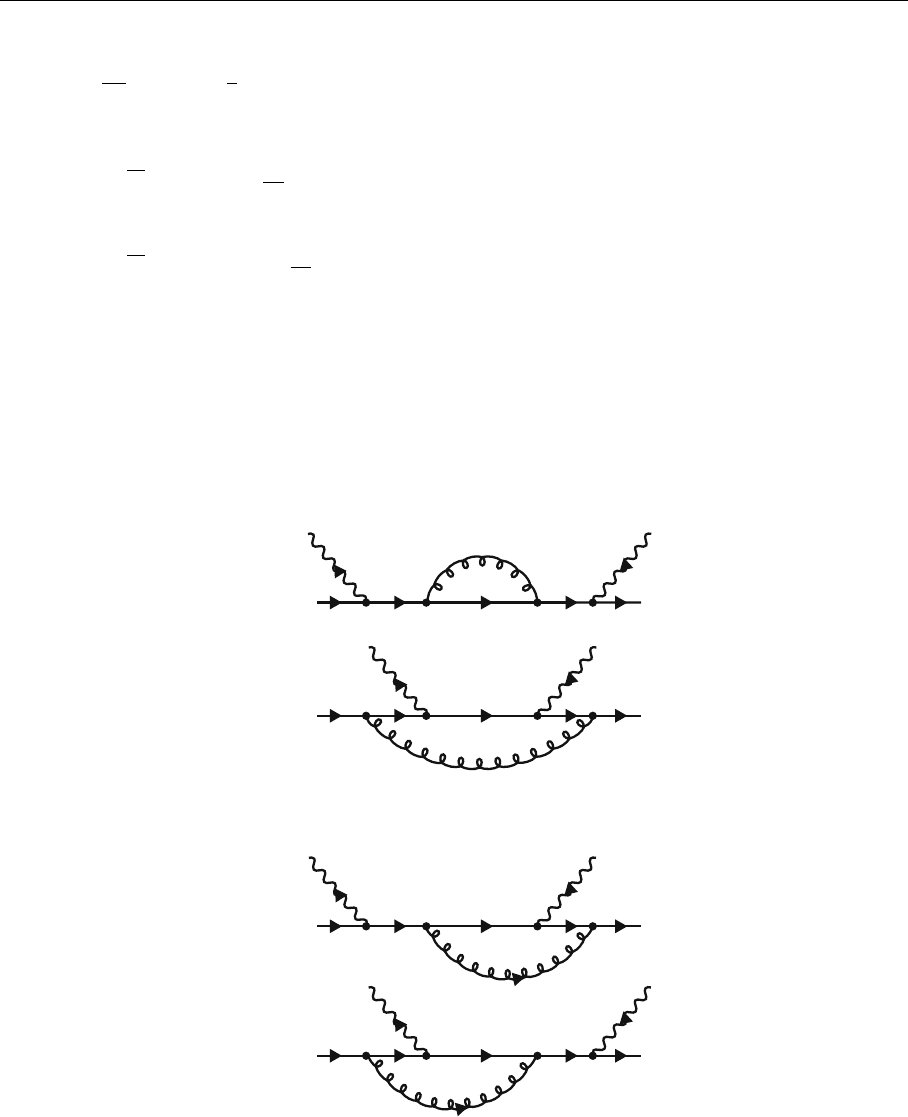
waves. To calculate the transition probabilities the graphs of Fig. 5.2 have to be

squared. This leads us to the calculation of the graphs depicted in Fig. 5.3. Note

that the intermediate propagators in Fig. 5.3 are on the mass shell because they

correspond to the outgoing gluons and quarks, which are real. Transforming this

into momentum space, we obtain the Feynman graphs of Fig. 5.3. We reiterate

q,m

(real)

q, 'm

K,a

K,a(real)

K,a

K(real)

p,i

p+q

p-K

p+q-K

p+q

p,i

Fig. 5.3.

The Feynman representation

of the corrections to W

µµ



shown in Fig. 5.1. The indi-

cation (real) at the gluon and

quark propagators draws at-

tention to the fact that the

intermediate quarks and glu-

ons in this graph are actually

the outgoing particles of the

process considered, i.e. they

are on the mass shell

242 5. Perturbative QCD I: Deep Inelastic Scattering

that here it must be taken into account that the outgoing (supposedly massless)

parton and the outgoing gluons are on the mass shell, i.e.,

( p +q −K )

= K

= 0 . (5.5)

The usual propagators therefore have to be substituted by δ functions if these

particles occur as “inner lines” in the W

µµ



graphs:

+iε

=P(1/K

) −πiδ(K

) →−2πiδ(K

)Θ(K

)

( p

−K

)

( p +q −K )

+iε

→−2πiγ

( p

−K

)δ[( p +q −K )

]

×Θ( p

−K

). (5.6)

The arrow → indicates that only the imaginary part of the Compton for-

ward scattering amplitude contributes to the scattering cross section. Using the

Feynman rules of Exercise 4.2 together with these modiﬁcations yields

µµ



⎡

⎣



a,i, j









⎤

⎦





∗ν









u(p, s)(γ



( p/ −K/)

−1



+γ



( p/ +q/)

−1



)

×( p/ +q/ −K/)Θ(p

−K

)δ



( p +q −K )



Θ(K

)δ(K

)



( p/ −K/)

−1

+γ

( p/ +q/)

−1



·u(p, s)



×(−4π

)

(2π)

2π

. (5.7)

Here we have averaged over spin s (this gives the second factor

:itisidentical

with the factor

stemming from the averaging over nucleon spin in (5.1)), quark

color i (this gives the factor

), and photon polarization ε of the initial state (this

gives the ﬁrst factor

). Note that the factor e

(charge squared) has been sep-

arated from W

µν

. The factor (−4π

) = (−2πi)

stems from the 2πi factors of

the gluon and quark propagators (5.6). Q

denotes the electric charge of the ﬂa-

vor f, and the additional factor 1/2π is due to (5.1)! In the Feynman gauge we

have



∗ν



=−g

νν



. (5.8)

Additional gauge terms that will appear, for example, in the Landau gauge will

be proportional to q

or q



and vanish if contracted with a conserved current.

See the discussion in W. Greiner and J. Reinhardt: Field Quantization (Springer Berlin,

Heidelberg 1996).

5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 243

We get









. (5.9)

Utilizing the projection operator



u(p, s)u( p, s) = p/, which is in our normal-

ization of the Dirac-spinors – see Sect. 2.1.4 – the correspondence to the relation



u(p, s)u( p, s) =

p/+m

wellknown from QED

, we obtain

µµ



8π

K tr



( p/ −K/)

( p −K )



+γ



( p/ +q/)

( p +q)



× ( p/ +q/ −K/)



( p/ −K/)

( p −K )

+γ

( p/ +q/)

( p +q)

&

×Θ(K

)Θ( p

−K

)δ







( p +q −K )



. (5.10)

Fortunately we do not have to evaluate the trace completely, since we already

know that all the information provided by W

µµ



is contained in the structure

functions W

and W

(see (3.18) and (3.32)). Therefore it is sufﬁcient to de-

termine p



µµ



and W

. We abbreviate the trace in (5.10) by S

µµ



and

delegate the evaluation of p



µµ



and S

to Exercise 5.2. The results are



µµ



= 4u , (5.11)

=−8



−



(5.12)

with the Mandelstam variables

t = ( p −K )

=−2p ·K ,

s = (q + p)

=2ν −Q

ν = p ·q ,

u = (q −K )

= (q + p −K − p)

=−2p ·(q + p −K ) =−2ν −t . (5.13)

W. Greiner and J. Reinhardt: Quantum Electrodynamics, 2nd ed., (Springer Berlin,

Heidelberg 1996).

244 5. Perturbative QCD I: Deep Inelastic Scattering

EXAMPLE

5.1 Photon and Gluon Polarization Vectors

Real photons and gluons have two physical degrees of freedom. Thus the sim-

plest choice would be (k is the photon or gluon momentum) that ε

and ε

are

deﬁned such that

(

)

(

)

,(ε

)

= (ε

)

=0 ,

1,2

·k =0 , and ε

·ε

=0 . (1)

The sum over the vector particle polarization is then



∗ν

)

0ifµ = 0orν = 0



ε=ε

,ε

∗ν

otherwise

. (2)

This, however, is not explicitly Lorentz invariant. Therefore it is advantageous

to choose different vectors. The three independent four vectors k

,ε

1µ

,ε

2µ

not completely span the four-dimensional space. For that reason we introduce an

additional vector n

. Then the following is a rather general covariant form:

µν



∗ν

=−g

µν

n ·k

−

(n ·k)

, (3)

that reduces to (5.6) for n

= (0, 0). This form has the property

µν

n ·k

−

(n ·k)

, (4)

which vanishes for real photons (k

= 0 !) as it should. Furthermore it fulﬁlls

µν

=−n

n ·k

−

n ·k

=0 , (5)

implying the gauge

=0 . (6)

The speciﬁc form of n

for the gauge one is interested in can be read off from (6).

We give two standard examples.

1. The Lorentz gauge. In this case n

= k

, so that (6) becomes k

=0, which

is the well-known deﬁnition of the Lorentz gauge. From (3) then follows

µν

(1) =−g

µν

−

=−



µν

−



. (7)

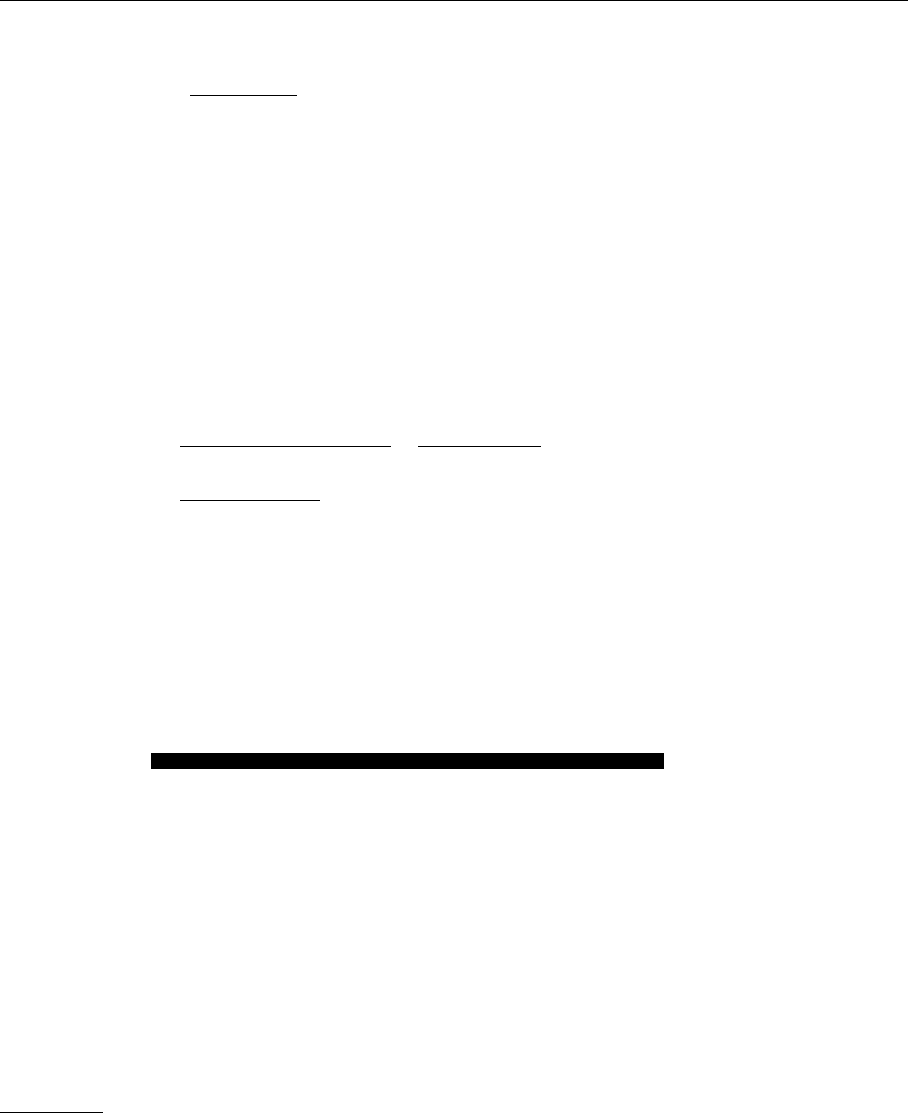
5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 245

2. The light-like gauge:

µν

(2) =−g

µν

n ·k

, (8)

where n

is the ﬁxed four-vector with n

= 0. Note, the fact that n

=0 sug-

gests the name “light-like” gauge. However, the form (3) also allows us to choose

according to the problem we are treating. It might be very advantageous to

choose, for example,

= k

+α p

, (9)

where p is one of the momenta of the problem. This might be useful, for ex-

ample, if k

=0andp

=0, which describe outgoing partons (with negligable

rest mass). Then (9) leads to

µν

=−p

k · pk

(

+α p

)

p ·k

α p ·k

−

2α k · pk· pk

(α p ·k)

=−p

+α p

−2k

=0 , (10)

and also

µν

=0 , (11)

which allows us to set all vectors p

, k

contracted with Σ

µν

equal to zero.

EXERCISE

5.2 More about the Derivation of QCD Corrections

to Electron–Nucleon Scattering

Problem. Evaluate S

and p



µµ



for the trace in (5.8).

Solution. First we employ

a/γ

=−2a/,

a/b/γ

=4a ·b ,

a/b/c/γ

=−2c/b/a/, (1)

E. Tomboulis: Phys. Rev. D 8, 2736 (1973).

Example 5.1

246 5. Perturbative QCD I: Deep Inelastic Scattering

Exercise 5.2

in order to simplify S

µµ



µµ



−2

( p −K )



p/( p/ −K/)γ



( p/ +q/ −K/)γ

( p/ −K/)



−2

( p −K )

( p +q)



p/γ

( p/ +q/)( p/ −K/)γ



( p/ +q/ −K/)



−2

( p −K )

( p +q)



p/γ



( p/ +q/)( p/ −K/)γ

( p/ +q/ −K/)



−2

( p −q)



p/γ



( p/ +q/)( p/ +q/ −K/)(p/ +q/)γ



. (2)

Then S

is brought into the form

( p −K )

[

p/( p/ −K/)(p/ −K/ +q/)( p/ −K/)

]

−

( p −K )

( p +q)

( p +q) ·( p −K )tr

[

p/( p/ −K/ +q/)

]

( p −q)

[

p/( p/ +q/)( p/ −K/ +q/)( p/ +q/)

]

. (3)

For massless quarks and real gluons, utilizing a/a/ = a

(γ

+γ

) =

µν

, one has

= p

= 0 ,

( p/ −K/ +q/)

=( p −K +q)

= 0 ,

( p −K )

=−2p ·K ,

because of the δ



( p +q −K )



function in (5.8)

( p/ +q/)( p/ −K/ +q/) =( p/ +q/ −K/ +K/)(p/ −K/ +q/)

=(p/ −K/ +q/)

+K/(p/ −K/ +q/) =+K/(p/ −K/ +q/) ,

( p/ −K/)(p/ −K/ +q/) =( p/ −K/ +q/ −q/)( p/ −K/ +q/)

=(p/ −K/ +q/)

−q/( p/ −K/ +q/) =−q/( p/ −K/ +q/) ,

( p +q)

=(p +q −K +K )

=2K ·( p +q −K ) =2K ·( p +q), (4)

which simpliﬁes (3) to

( p ·K)

[

p/q/( p/ −K/ +q/)K/

]

p ·KK·( p +q)

( p +q) ·( p −K )4p ·(q −K )

[K ·( p +q)]

[

p/K/(p/ −K/ +q/)q/

]

5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 247



( p ·K )

[K ·( p +q)]



[

2(p ·q)(p ·K )

]

( p ·K )(K ·( p +q))

( p +q) ·( p −K ) p ·(q −K ). (5)

Next we introduce the Mandelstam variables

t = ( p −K )

=−2p ·K ,

s = ( p +q)

= 2K ·( p +q) = 2 p ·q ,

u = (q −K )

=(q −K + p)

−2 p ·(q −K + p) + p

=−2p ·(q −K ). (6)

Taking into account

≡−q

=−(q + p − p)

=−2K ·(p +q) +2p ·(q + p)

=2(q + p) ·( p −K ), (7)

we ﬁnally obtain

=−8

−8

+16

=−8



−2



. (8)

Now we evaluate the scalar p



µµ



in a completely analogous manner. From

(2) follows



µµ



−2

( p −K )

[

p/( p/ −K/)p/( p/ −K/ +q/) p/( p/ −K/)

]

. (9)

All other terms vanish because p/

= p

=0, and therefore (9) simpliﬁes futher



µµ



−2

( p −K )

[

p/K/ p/(−K/ +q/) p/K/

]

. (10)

The ﬁnal simpliﬁcations are achieved by exchanging the ﬁrst two factors under

the trace

p/K/ = p

= p

(2g

µν

−γ

) = 2 p ·K −K/ p/

and therefore



µµ



−4

( p −K )

p ·K tr

[

p/(−K/ +q/) p/K/

]

+0 . (11)

Exercise 5.2