Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

248 5. Perturbative QCD I: Deep Inelastic Scattering

Exercise 5.2

Fig. 5.4. Kinematics of the

graphs depicted in Fig. 5.2

in the Breit system

A similar exchange of the last two factors yields



µµ



−8

( p −K )

( p ·K )

[

p/(q/ −K/)

]

−8

( p −K )

( p ·K )

·4p ·(q −K )

=−8p ·(q −K ) =4u . (12)

In the last step one of the relations (4) and (6) has been used.

Since the traces in (5.11) and (5.12) are Lorentz invariant, the K integration can

be performed in an arbitrary reference system. We choose the Breit system (see

Chap. 3), i.e.,

=( p, 0, 0, −p), q

=(0, 0, 0,

). (5.14)

The corresponding kinematics is depicted in Fig. 5.4. The determination of W

µµ



in (5.10) is leading us to integrals of the following form

I =

Kf(Q

, t,ν)Θ(K

)Θ( p

−K

)δ(K

)δ



( p +q −K )



I =

dK dΩ

f(Q

, t,ν)Θ(p

−K

)

×δ(K

−K

)δ



( p +q −K )



Since the process considered is clearly cylindrically symmetric, the K

and ϕ in-

tegrations can be performed immediately: Using δ(K

−K

) = δ(K

−K )/2K

yields

I = 2π

∞

−1

dcosθ f(Q

, t,ν)

Θ( p

−K )δ



( p +q −K )



(5.15)

Here f(Q

, t,ν)is any function depending on the Mandelstam variables (5.13),

which will be speciﬁed later. Next we rewrite the second δ function by inserting

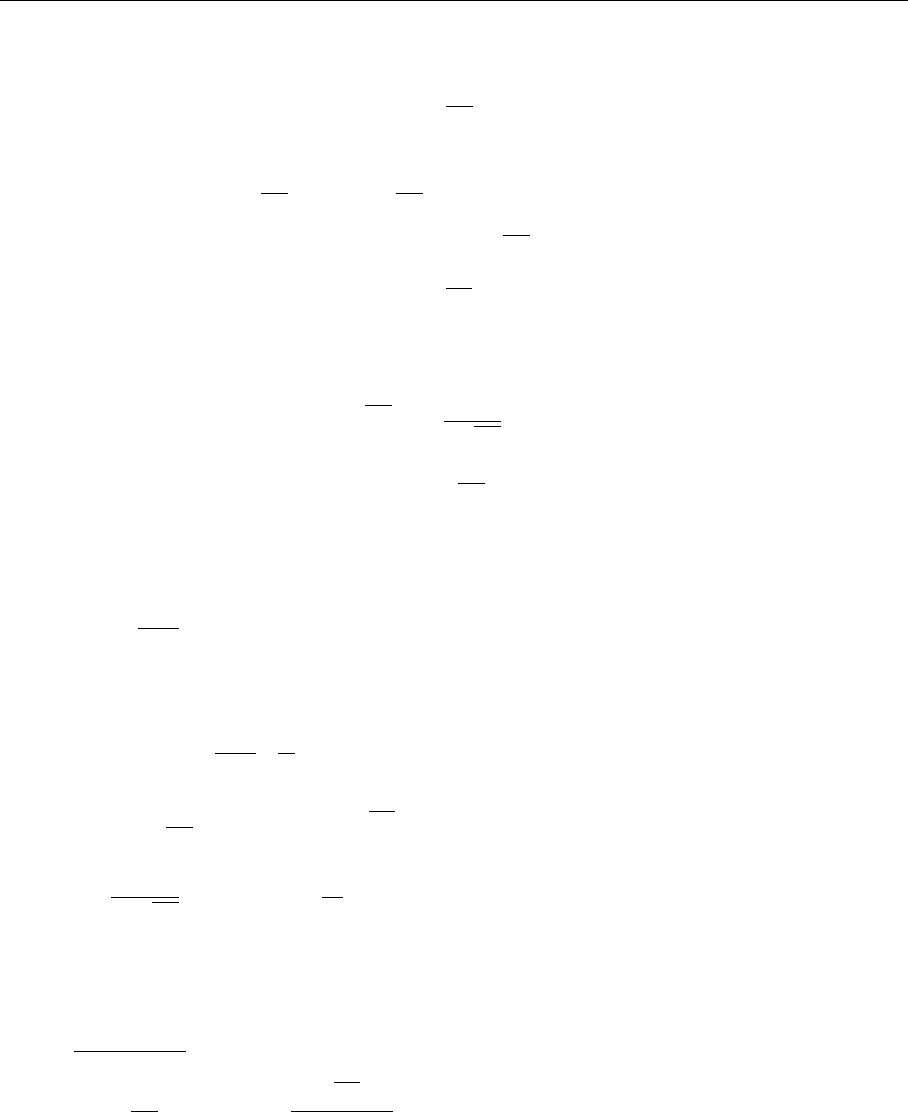
5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 249

the explicit form of K

=(K, 0, K sin θ, K cos θ) , (5.16)

( p

−K

)



p −K, 0, −K sin θ, −p +

−K cos θ



= p

−2 pK −



+ p

+2 pK cos θ

−2K

cos θ −2p



=−2pK(1 +cos θ) −Q

+2ν +2K

cos θ. (5.17)

Note that in the Breit system (5.14) ν = p ·q = p ·

, which entered (5.17).

Now cos θ is replaced by t. According to (5.13) we get with (5.14) and (5.16)

t =( p

−K

)

=−2pK(1 +cos θ) , (5.18)

( p

−K

)

=t −Q

+2ν −2K

+2K

p(1+cos θ)

(5.19)

=t(1 −Q

/ν) −Q

+2ν −2K

. (5.20)

Finally, according to (5.18), and remembering that p and K are ﬁxed, we replace

dcosθ by

dcosθ →−

2pK

dt (5.21)

and obtain

I = 2π

∞



−1

2pK



Θ( p

−K )

×δ





1 −



−Q

+2ν −2K



f(Q

, t,ν)

=−

dtf(Q

, t,ν)=

4ν

dtf(Q

, t,ν) . (5.22)

The boundaries of the t integration are not yet determined. This is achieved by

substituting K from (5.16) into the argument of the δ function:

K =

−t

2p(1+cos θ)

, (5.23)

0 = t



1 −



−Q

+2ν +

p(1+cos θ)

. (5.24)

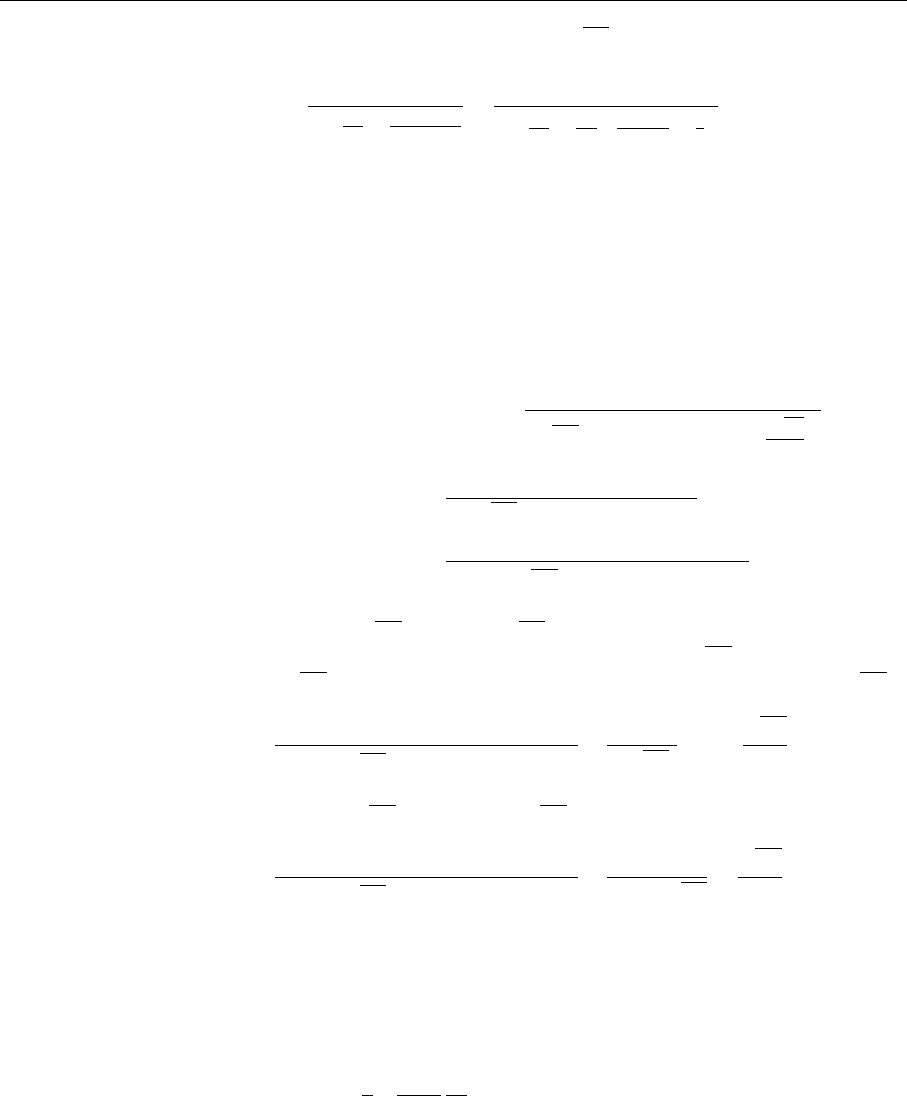
250 5. Perturbative QCD I: Deep Inelastic Scattering

The second equation yields for t



ν =

· p



t =

−2ν

1 −

ν(1+cos θ)

−2ν

1 −

2ν



1+cos θ

−



. (5.25)

Since x = Q

/2ν is less than or equal to one (see (3.42)), the denominator is big-

ger than or equal to zero. The numerator is always less than or equal to zero and

consequently t is a monotonically decreasing, negative function of cos θ.The

boundaries t

and t

are simply

= t(cos θ =−1) = 0 , t

= t(cos θ =1) =−2ν. (5.26)

Now we have to investigate whether the Θ function leads to further restrictions.

With (5.23), (5.25), and (5.14)

−K

= p −K = p −

2ν −Q

+2 p(1 +cos θ)



1 −

√



= p −

2ν −Q

−2

cos θ +2p(1+cos θ)

= p −

2ν − Q



4p −2



cos θ +2p(1−cos θ)

. (5.27)

Because x =

/2p ≤ 1 ⇒

≤ 2p, the denominator is always positive.

It assumes its smallest value at cos θ =−1forp >

and at cos θ = 1for

p <

. Let us now consider these two cases separately, i.e., for p >

2ν −Q



4p −2



cos θ +2p(1−cos θ)

≤

2ν −Q

= p −

≤ p , (5.28)

because ν =

p,andforp <

2ν −Q



4p −2



cos θ +2p(1−cos θ)

≤

2ν −Q

4p −2

≤ p . (5.29)

Hence the argument of the Θ function is positive deﬁnite:

−k

≥ p − p = 0 . (5.30)

Thus, from (5.10) and (5.22) we obtain the result

µµ



=−

16π

8ν

−2ν

dtS

µµ



, (5.31)

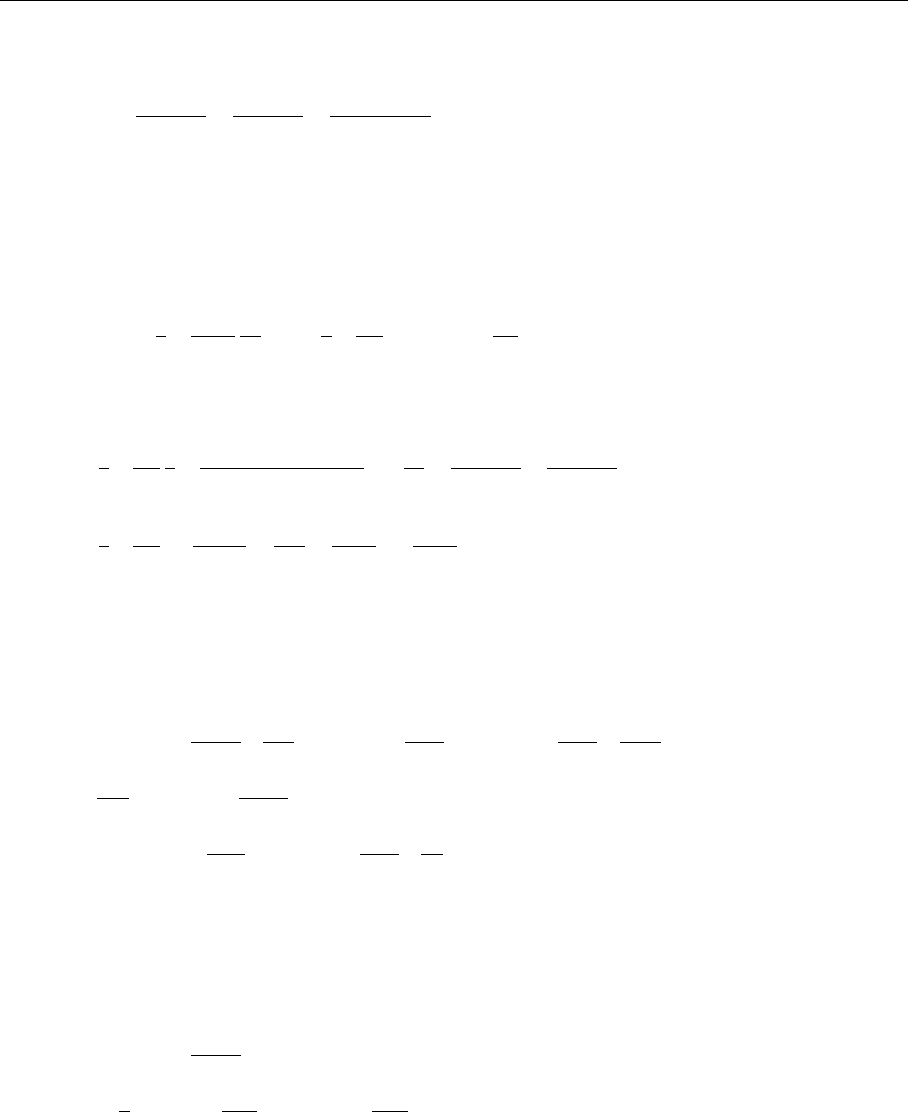
5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 251

and from (5.11) and (5.12)



µµ



= 4u =−4(2ν +t), (5.32)

=−8



2ν −Q

(2ν +t)

t(2ν − Q

)



. (5.33)

The t integration yields a logarithmic singularity for S

, which is the

same kind of infrared singularity that occurs in the evaluation of the QED

bremsstrahlung cross section. In fact the graphs in Fig. 5.1 can also be interpreted

as bremsstrahlung processes. Before we discuss this singularity further, how-

ever, we should like to ﬁnish our calculation. First, inserting (5.11) into (5.31) is

without any problem and yields



µµ



16π

2ν

8π

2ν, α

4π

. (5.34)

Second, inserting (5.12) into (5.31) leads to a logarithmically divergent integral,

which we cut off at −λ

4π

⎛

⎜

⎝

(2ν −Q

)

+4νQ

(2ν −Q

)

−λ

−2ν

2ν −Q

2ν

2ν − Q

⎞

⎟

⎠

4π



1 +x

1 −x

−

1 −x



. (5.35)

Here, again, x = Q

/2ν has been introduced. Next we answer the question: How

are the structure functions W

and W

or F

and F

, respectively, connected with

the expressions in (5.34) and (5.35)? First remember the connection between F

and W

and between F

and W

, respectively. The Fs were introduced in (3.43).

Adopting them, equations (3.18) and (3.43) yield the relation

µµ



−g

µµ







−q

q · P





−q



q · P





−g

µµ







−q

q · P





−q



q · P





. (5.36)

µµ



is the scattering amplitude for leptons (transmitted by photons) at nucle-

ons. Here the factor 1/M

is convenient. The scattering amplitude for leptons

at quarks, W

µµ



, is deﬁned without the 1/M

factor. This is convenient since

one deals with massless quarks. The corresponding structure functions are now

denoted by F

and F

, respectively. For quarks, (5.36) therefore becomes

µµ



−g

µµ







−q

q · p





−q



q · p



. (5.37)

252 5. Perturbative QCD I: Deep Inelastic Scattering

It follows with Q

=−q

and p

= 0 (massless quarks!) that

= (−4 +1)F



−2

(q · p)



=−3F

(5.38)

and similarly



µµ



=−



−2xF



. (5.39)

Obviously p



µµ



is a measure for the violation of the Callan–Gross rela-

tion:

=2xF

(5.40)

by the interaction. It is now clear that instead of the two scalars W

and



µµ



one may choose F

and F

(or any other linearly independent

combination). The connection between both follows from (5.38) and (5.39) as

(x, Q

) =−



µµ



(x, Q

) =−xW

+12



µµ



. (5.41)

Using the results (5.34) and (5.35) the additional contributions to these quark

structure functions due to “gluon bremsstrahlung” (see Fig. 5.1) are therefore

∆



(x, Q

)−2xF

(x, Q

)



, (5.42)

∆F

(x, Q

) =

2π

−

4π



1 +x

1 −x



+ln x



4x −1

1 −x

&

≈−

2π

1 +x

1 −x

ln λ

+... , (5.43)

where we have retained only the logarithmic Q

-dependent term, which will

dominate for Q

→∞. Now we investigate the dependence of the nucleon struc-

ture functions F

1,2

on the quark structure functions F

and F

.Tothisendwe

5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 253

have to go back to (3.70)–(3.82). In particular, according to (3.81), F

is given

(X, Q

) =



(X, Q

·X



dξ

(ξ

, Q

δ(ξ

−X) (5.44)

with

= ξ

and

dξ

f(ξ

) = 1 .

X denotes Q

/2P

·q while x is equal to Q

/2p ·q.Theξ

is the fraction of the

ith parton of the total momentum P

and f(ξ

) is the probability that a parton will

have that momentum. Q

denotes the charge of the ith parton. By deﬁnition the

structure functions are factors in the scattering tensor, which turn the contribu-

tions of free pointlike particles into those of extended particles. Correspondingly

one has to multiply the right-hand side of (5.44) by the factor F

(x, Q

) and to

modify the δ function according to

x =

2p ·q

2ξ

·q

, (5.45)

(X, Q

) =



dξ

(ξ

Qu,i



, Q





dξ

(ξ

)ξ

dx δ(X −xξ

Qu,i

(x, Q

). (5.46)

The last step in (5.46) is easily veriﬁed. Note that we have integrated over all

values of x that contribute to a given X. One might look for a missing factor Q

However, this is contained in F

Qu,i

. With the help of (5.43) we ﬁnally obtain

the following contribution of the graphs in Fig. 5.1 to the nucleon structure

function F

of deep inelastic electron–nucleon scattering:

∆F

(X, Q

)

bremsstrahlung

=∆F

(X, Q

) −∆F

(X, Q

)

=−

2π



⎡

⎣

dξ

f(ξ

)ξ



x −





1 +x

1 −x







⎤

⎦

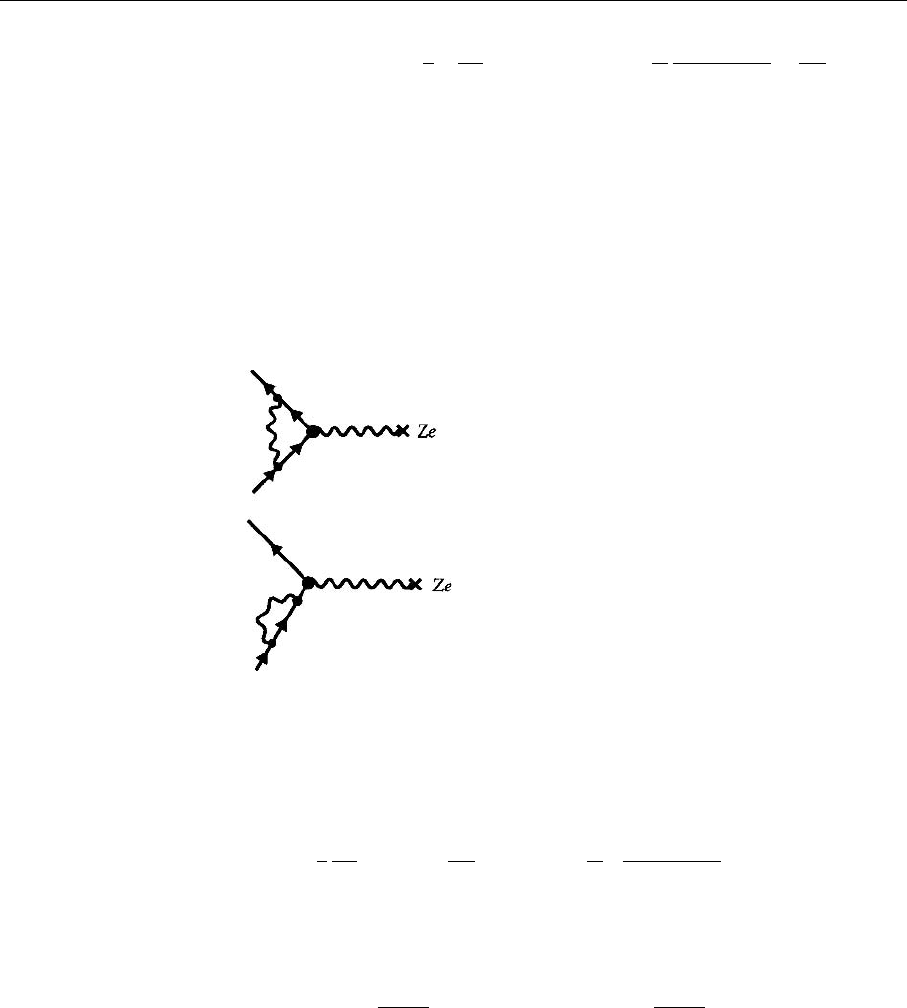
254 5. Perturbative QCD I: Deep Inelastic Scattering

=−

2π



dξ

f(ξ

)

1 +(X/ξ

)

1 −(X/ξ

)

, (5.47)

where the lower boundary of integration is due to the fact that ξ

> X (see

(5.45)). The integral is divergent, because the integrand has a singularity at

X = ξ

or x = 1. Since x = 1 means elastic scattering, the gluon emitted in this

reaction carries neither energy nor momentum. The occurrence of such an in-

frared divergence is not surprising: one encounters similar behavior in QED

bremsstrahlung. There it can be shown that, up to a given order in α, the infrared

divergences cancel each other if all scattering processes, including the elastic

channel, are taken into account. To lowest order this is achieved by the following

additional graphs:

Many more graphs exist in QCD and an analogous proof is more sophisti-

cated. The desired compensation can, to lowest order, be shown by an explicit

evaluation. The result can be brought into the following form:

∆F

(bremsstrahlung +radiative corrections)

≈−

2π



dξ

(ξ

)



1 +(X/ξ

)

1 −(X/ξ

)



, (5.48)

where [(1 +z

)/(1 −z)]

is deﬁned by

dzF(z)



1 +z

1 −z



[

F(z) −F(1)

]

1 +z

1 −z

(5.49)

for every sufﬁciently regular function F(z). Keep in mind that Q

denote the

squares of the charges of the various quarks, while Q

and Q

stand for the

two squared momentum transfers. The virtual diagrams which have to be taken

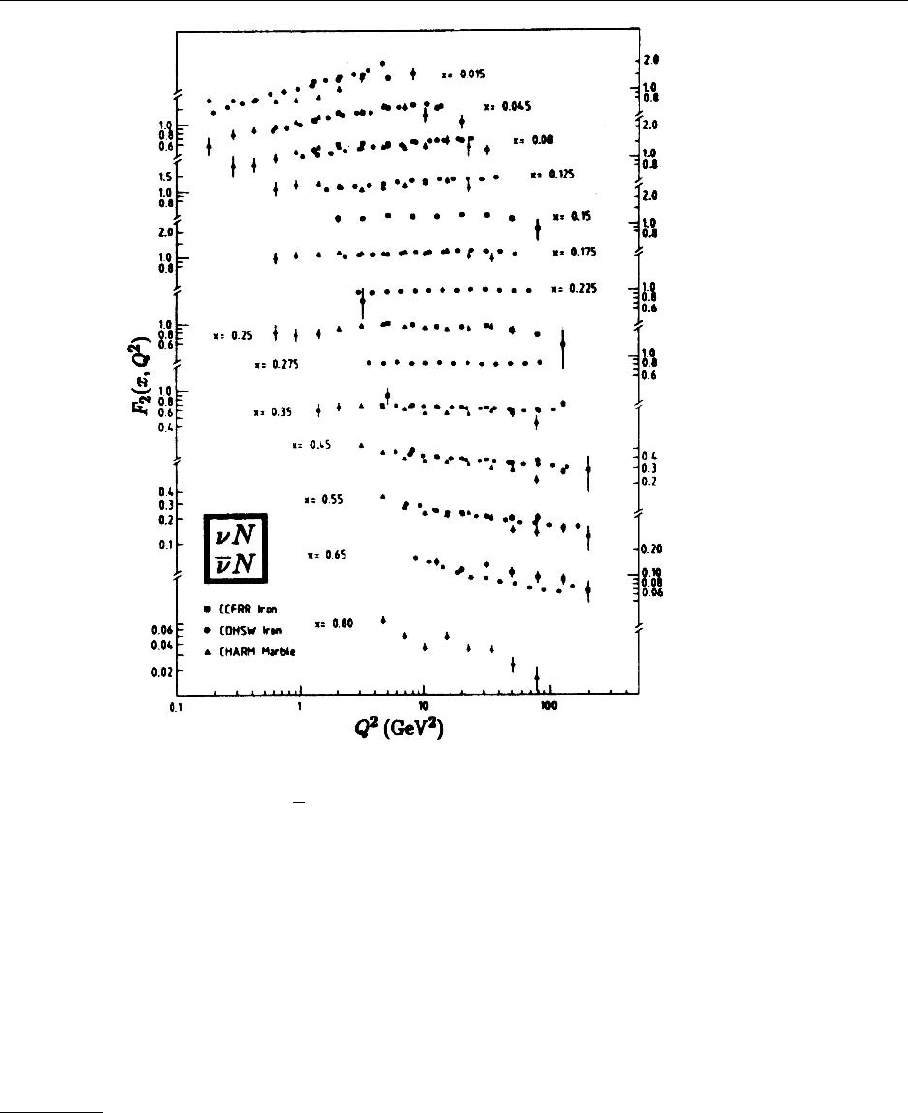
5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 255

Fig. 5.5. The structure func-

tions of neutrino–nucleon

scattering. (From Review of

Particle Properties, Physical

Review D 45 (1992))

into account regularize the 1/(1 −

) singularity in (5.47) so that (5.48) holds.

That such a cancellation has to occur can be understood by rather general argu-

ments. The Bloch–Nordsieck theorem assures that infrared divergences cancel

in inclusive cross sections.

(From now on we shall again write x for X.) One

possible choice for f(ξ

) is the distribution function derived in the context of

the simple parton model (see Fig. 3.11). In this case the result would be an

expression for the scale violation of the function F

depending on one ﬁt parame-

ter α

. From Fig. 3.5 it is clear that for x > 0.5 scale violations in fact occur, i.e.,

becomes a function of x and Q

. In order to be more precise, F

decreases

with increasing Q

for x > 0.5. The very same behavior can also be encoun-

tered in other scattering processes, e.g., in neutrino–nucleon scattering (Fig. 5.5).

Here it is seen that for small x the Q

dependence is just the opposite, i.e., for

F. Bloch and A. Nordsieck: Phys. Rev. 52 (1937) 54.

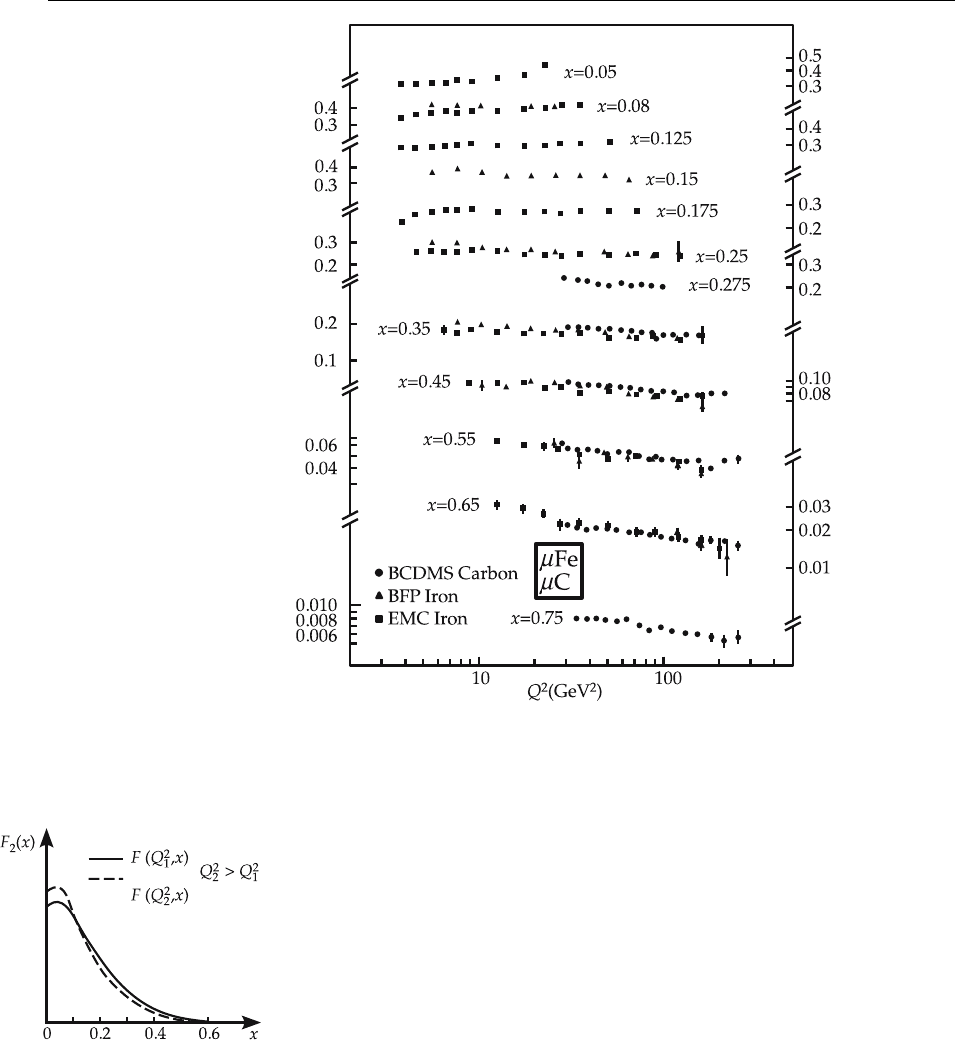
256 5. Perturbative QCD I: Deep Inelastic Scattering

Fig. 5.6. Structure functions

of muon–carbon and muon–

iron scattering. (From Re-

view of Particle Proper-

ties, Physical Review D 45

(1992))

Fig. 5.7a. The schematic

dependence of the struc-

ture functions on Q

, with

 Q

x < 0.1 F

increases with Q

. The data in Fig. 5.6 show the same tendency for

electron–nucleon scattering and muon–nucleon scattering.

The overall behavior (see Fig. 5.7) is readily understood. For increasing mo-

mentum transfers QCD processes become more important, and on average more

quarks, antiquarks, and gluons occur, between which the total momentum is

distributed. Owing to (3.82), F

is given by

(x, Q

) =



(x, Q

x , (5.50)

i.e., by x times the probability that a parton carries the momentum fraction x.

(x, Q

) decreases for large x values with increasing Q

. This can be rec-

ognized by inspection of Fig. 5.7a, which illustrates the interacting quarks

in a nucleon. With higher momentum transfer Q

the number of partons in

a nucleon increases. Because now the total momentum of the nucleon is dis-

tributed over more partons, the distribution function f

(x, Q

) has to decrease,

5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 257

particularly for large x. Since the total momentum is constant,



(x, Q

)x = 1 , (5.51)

an enhancement for small x values should follow. However, this can be prevented

by the charge factors, for example, by Q

in (5.48). In this way the gluons con-

tribute to the sum (5.51), but not to the F

structure functions. As a matter of

fact, according to Chap. 3, the charged partons alone contribute only about 50%

to (5.51) (see explanation to (3.88)).

Structure functions for muon–carbon and muon–iron scattering are depicted

in Fig. 5.6. Again the same Q

dependance is observed. Furthermore, it is re-

markable that in the region 0.5 < x < 0.65 and for very small x the F

function

for iron is considerably smaller than for µ–p scattering. Part of this discrep-

ancy is due to the difference between neutrons and protons (the sums of the

squared charges of the quarks have a ratio of 3 to 2). The remainder of the dis-

crepancy is known as the EMC (European muon collaboration) effect, recalling

the experimental collaboration that ﬁrst discovered the effect.

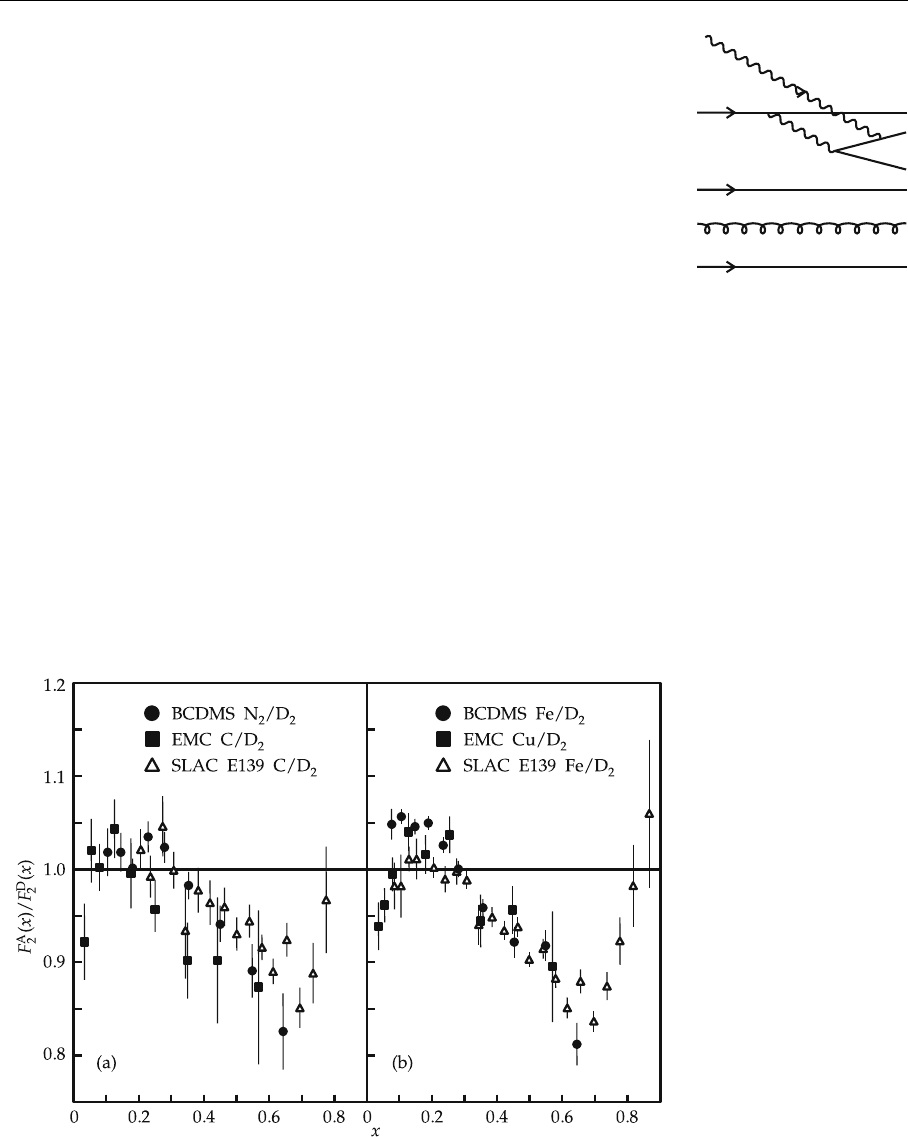
The history of the EMC effect has been quite involved. Eventually it was

found that part of the originally observed effect was due to an incorrect meas-

urement, since data analysis for small x values is extremely difﬁcult. However,

it is now clear that the structure functions depend on the size of the nucleus.

Figure 5.8 gives recent experimental results.

A number of theoretical models for the observed phenomena exist, but their

physical meaning is still heavily disputed. If we disregard this problem, pertu-

Fig. 5.8. The EMC effect:

the ratio of F

for carbon,

nitrogen, iron, and copper

to F

for deuterium (From

Review of Particle Proper-

ties, Physical Review D 45

(1992))

Fig. 5.7b. Contribution to

the small x domain visible at

higher Q

. At higher Q

ad-

ditional partons are visible,

because more qq pairs can

be excited. They contribute

mostly at small x