Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

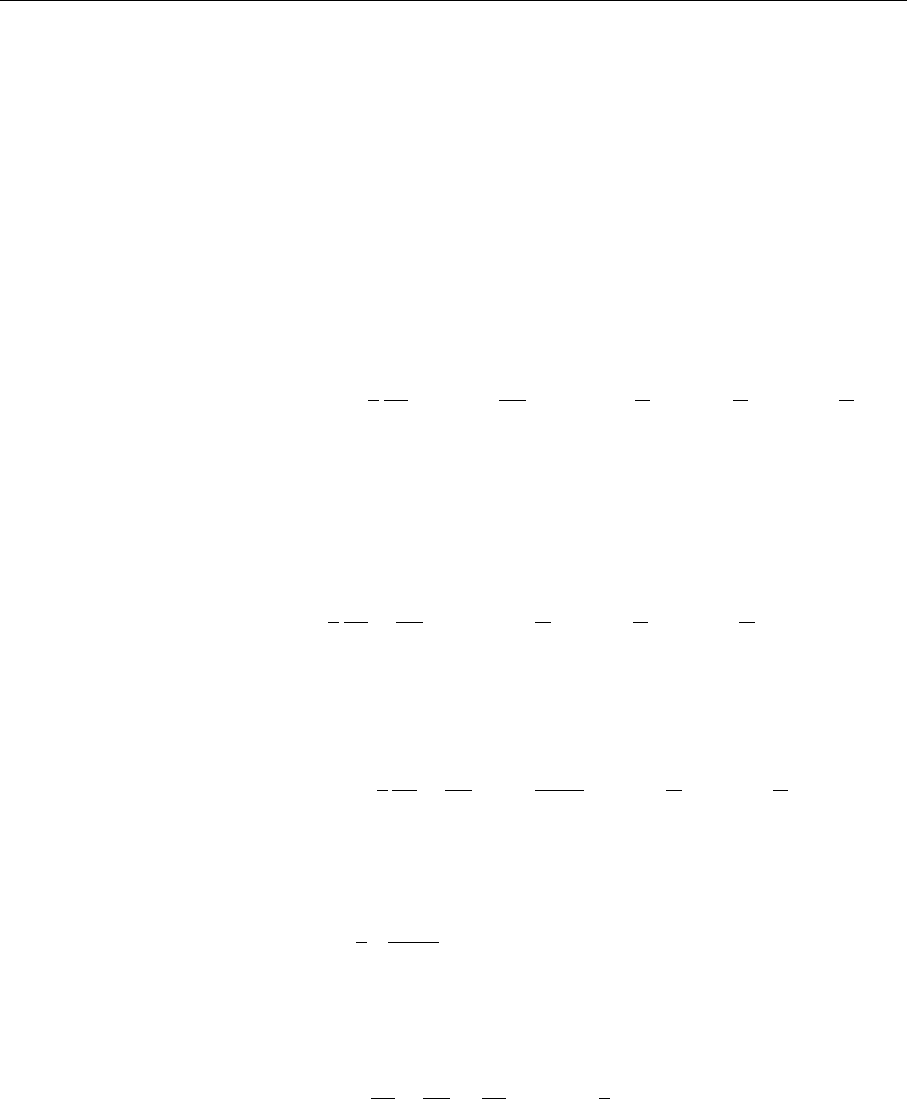
258 5. Perturbative QCD I: Deep Inelastic Scattering

bative QCD yields a reasonable description of the structure functions. To this

end, further corrections besides the gluon–bremsstrahlung correction have to

be taken into account. They could of course be determined graph by graph,

but there is a more elegant way to evaluate these corrections. Every calculation

again and again employs the same techniques and the speciﬁc kinematics of the

parton picture. Thus it is useful to formulate a general scheme suited for the spe-

cial situation of deep inelastic scattering. In this way we are led directly to the

Gribov–Lipatov–Altarelli–Parisi equations, which we derive here in an intuitive

fashion. Later on we discuss a more formal derivation.

First we rewrite the result of the bremsstrahlung calculation. Inserting (5.50)

into (5.48) (remember that we replaced X → x again) yields

∆F



∆ f

(x)Q

≈−

2π



dξ

(ξ

)

'

1 +





(



1 −



−1



0 =



⎡

⎣

x∆ f

(x)

2π

dξ

(ξ

)

'

1 +





(



1 −



−1



⎤

⎦

. (5.52)

Since the different quarks are considered to be independent, every single term in

the sum must be equal to zero:

∆ f

(x) =−

2π

dξ

(ξ

)

'

1 +





(



1 −



−1



(5.53)

We deﬁne

(z) =

1 +z

1 −z

. (5.54)

Furthermore, the index i is omitted, which, together with the replacement ξ

ξ = y,gives

∆ f(x) =−

2π

f( y)P





. (5.55)

5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 259

The omission of the quark index i indicates that, at this level, all quarks are

considered equal. Now, we deﬁne the logarithmic momentum variable

t(Q

) = ln

∆t =t(Q

) −t(Q

) = ln

, (5.56)

which gives

∆ f(x)

∆t

2π

f( y)P





. (5.57)

The last equation is only valid for small ∆t. Indeed, for large ∆t values it must

be taken into account that α

also depends on Q

and also f( y) → f( y, t).The

correct equation is therefore:

d f(x, t)

(t)

2π

f( y, t)P





. (5.58)

Equation (5.58) is already a Gribov–Lipatov–Altarelli–Parisi (GLAP) equation.

All further QCD corrections are described by additional terms on the right-hand

side.

We will discuss the physical meaning of this equation in more detail below.

However, we would ﬁrst like to remark that the expression [(1 +z

)/(1 −z)]

can be written in different ways. Two of those used more frequently in the

literature are the following:



(z) =



1 +z

(1 −z)

δ(1 −z)



, (5.59)

and



(z) =−

(1 +z) +2δ(1 −z)

+ lim

η→0

⎛

⎝

1 −z +η

−δ(1 −z)



1 −z



+η

⎞

⎠

. (5.60)

The equivalence of (5.59) and (5.60) with (5.54) can be proven by applying them

to an arbitrary smooth and continous function.



(z) f(z)dz =



1 +z

1 −z

f(z) −

1 −z

f(1)



f(1)



1 +z

1 −z

f(z) −

1 −z

f(1) +(1 +z) f(1)



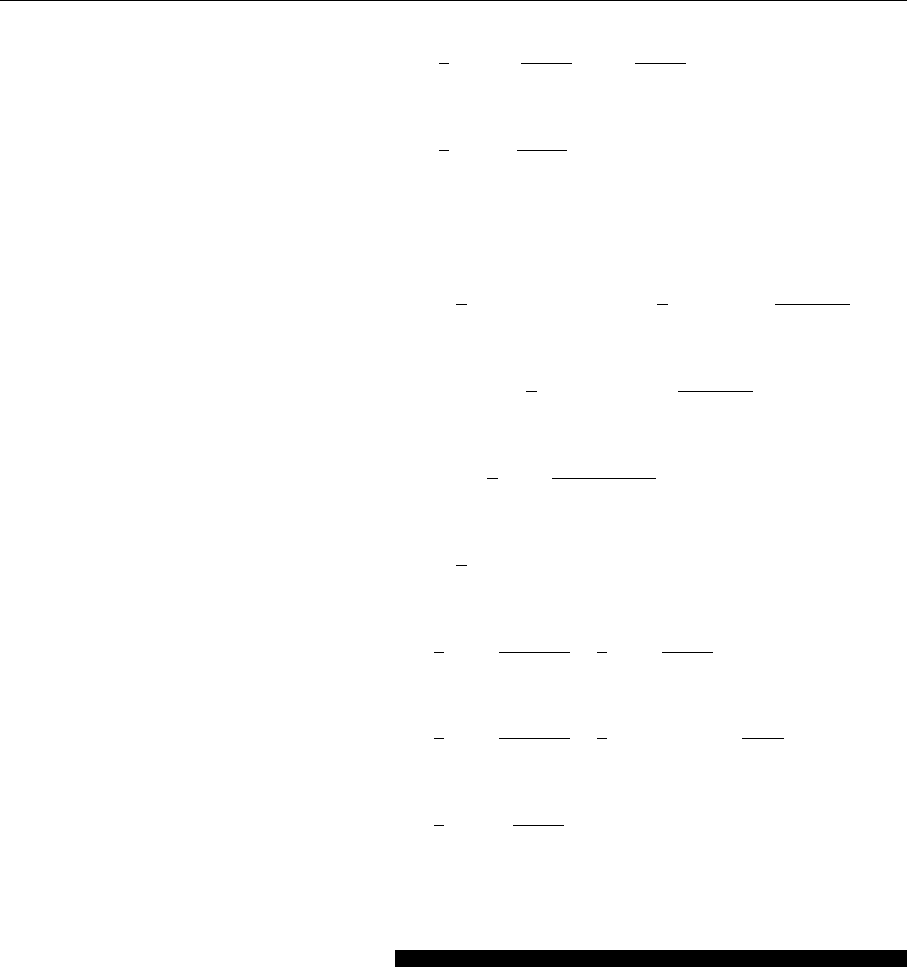
260 5. Perturbative QCD I: Deep Inelastic Scattering



1 +z

1 −z

f(z) −

1 −z

f(1)



1 +z

1 −z

f(z). (5.61)

For P



(z) a similar calculation can be performed:



(z) f(z)dz =−

⎛

⎝

f(z)(1 +z) +

lim

η→+0

1 −z +η

f(z)

⎞

⎠

+2 f(1) −

f(1) lim

η→+0

1 −z +η

= lim

η→+0

{1 −z +η}

f(z)

−

[

f(z)(1 +z) − f(1)(1+z)

]

f(z)

{1 −z}

−1

1 −z

[

f(z) − f(1)

]

f(z)

{1 −z}

dz(z

−1)



f(z)

1 −z





1 −z



f(z). (5.62)

EXERCISE

5.3 The Bremsstrahlung Part of the GLAP Equation

Problem. The bremsstrahlung process of Fig. 5.1 does not change the number

of quarks or antiquarks. Prove that this statement is also contained in the GLAP

equation (5.58).

5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 261

Solution. The number of quarks with a speciﬁc ﬂavor is given by

N =

dxf(x). (1)

One has to show that N does not depend on Q

and consequently not on t.

Therefore

N =

d f

2π

f( y)P





(2)

must vanish. We exchange the x and y integrations,

N =

2π

f( y)P





, (3)

and introduce the new variable z = x/y,

N =

2π

dyf( y)

dzP

(z) =

2π

dzP

(z). (4)

By means of (5.49) we have



1 +z

1 −z





−



1 +z

1 −z

= 0(5)

and hence

N =0 ,

which was to be shown.

It is no coincidence that the right-hand side of (5.58) integrated over x

separates into two factors, namely the integrals over y and z.SinceQCDis

a dimensionless theory, P

can only depend on ratios of the momenta that occur,

i.e., on x/y. Consequently all contributions to the GLAP equation exhibit the

same feature. In the next section we shall discuss how this mathematical structure

can be derived from very general assumptions.

Exercise 5.3

262 5. Perturbative QCD I: Deep Inelastic Scattering

(a)

(b)

Fig. 5.9a,b.

An illustration of the GLAP

equation. Larger values of

 Q

)resolve

smaller structures. (a)The

non-resolved vertex at low

(= Q

).(b) A particular

vertex structure at high

(= Q

)

The content of (5.58) can also be interpreted in the following way: owing to the

QCD interaction a quark can split up into a couple of particles with the same total

charge, for example, into a quark and a gluon or into two quarks, one antiquark,

and a gluon.

Now the question arises whether the quark “ﬁne structure” can be resolved by

the exchanged photon. Clearly this depends on the photon momentum. For larger

values of Q

smaller structures which might exist only for shorter times become

visible (see Fig. 5.9). In this sense P

is also denoted a “splitting function”and

interpreted as the probability that a quark shows the inner structure quark + gluon

at a resolution of t = ln(Q

). Now it is easy to guess in what way one has to

generalize (5.56) in order to describe the following processes also:

and

First we introduce new symbols. The single quark distribution functions q

(x)

and

(x) are replaced by a total quark distribution,

Σ(x) =





(x) +q

(x)



, i = u, d, s, c,... , (5.63)

and by differences between the quark distributions,

∆

(x) = q

(x) −q

(x), (5.64)

∆

(x) −q

(x), (5.65)

V(x) =



(x) −q

(x)) . (5.66)

Usually Σ(x) is referred to as a singlet distribution function, since it is symmetric

in all ﬂavors (it transforms as a singlet in the ﬂavor symmetry group). V(x) mea-

sures the valence quark distribution. If we assume q

(x) = q

(x), q

(x) = q

(x),

etc., we have for the proton V(x) = q

(x) −q

(x) +q

(x) −q

(x) = u

val

(x) +

val

(x), and due to the isospin of the proton the sum rules,

val

(x) dx =2

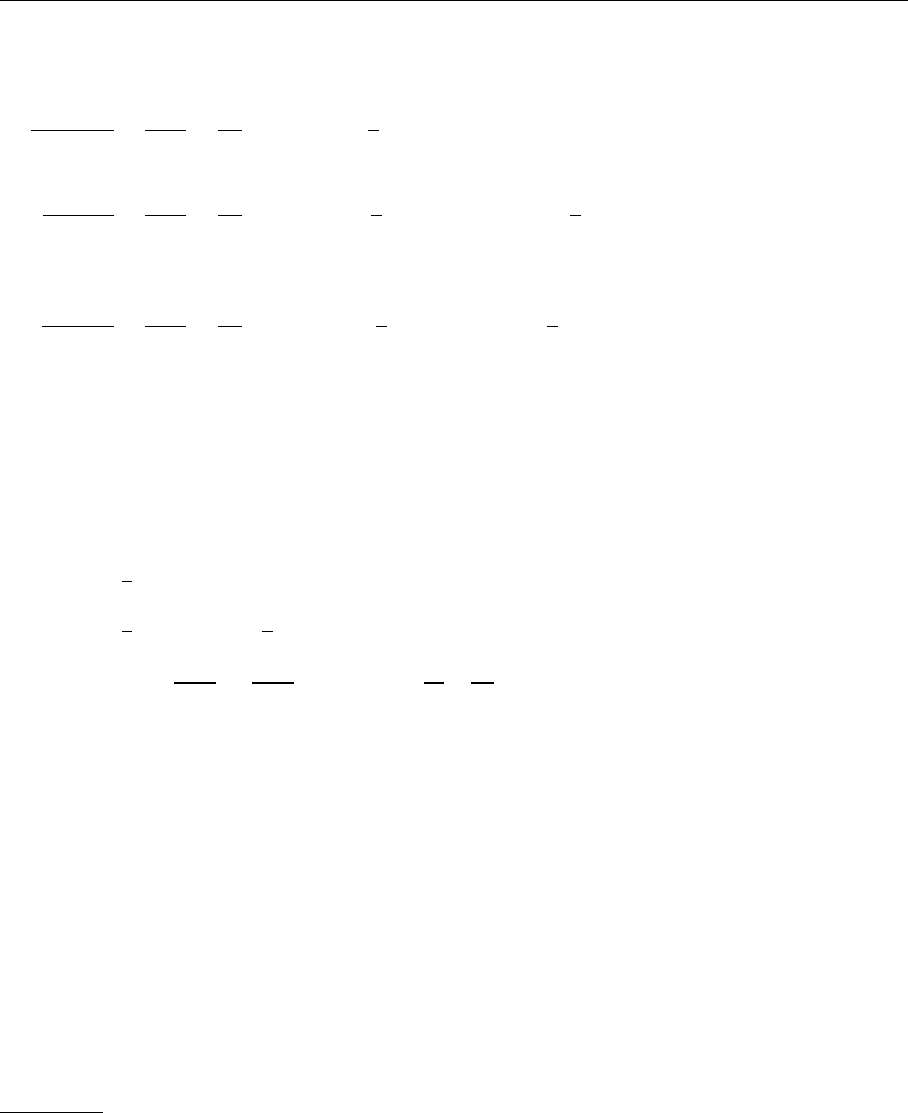
5.1 The Gribov–Lipatov–Altarelli–Parisi Equations 263

and

val

(x) dx =1 hold. A GLAP equation can be derived for each of these

distribution functions. They read

d∆

(x, t)

(t)

2π

∆

( y, t)P





, (5.67)

dΣ(x, t)

(t)

2π



Σ( y, t)P





+2N

G( y, t)P





(5.68)

dG(x, t)

(t)

2π



Σ( y, t)P





+G( y, t)P





(5.69)

Remember, t = ln(Q

) and ∆

(x, t = 0) has been simply denoted as ∆

(x)

in (5.64). The same holds for the other quantities. Here in (5.67)–(5.68), G(x, t)

and N

denote the gluon distribution function and the number of ﬂavors;

, P

,andP

correspond to the above graphs, respectively. A calculation

analogous to the one discussed above yields

(z) =



+(1 −z)



, (5.70)

(z) =



1 +(1 −z)



, (5.71)

(z) = 6





1 −z



1 −z

+z(1−z) +



−



δ(1 −z)



(5.72)

The derivation of the explicit expressions (5.70)–(5.72) is quite cumbersome,

some of them will be treated in Examples 5.5–5.7

The general structure of

(5.67)–(5.69) on the other hand is very simple. The bigger Q

, the more par-

tons with decreasing x are resolved. Therefore only such processes occur on the

right-hand side, that increase the particle number.

It should be clear how to interpret the splitting functions P

, P

,and

. It seems to be natural to interpret, for example, P

(x/y) as the probability

density of ﬁnding a quark around a quark with fraction x/y of the parent quark

momentum y. This clearly leads to a change of the parent quark density



( y, t)



(x, t). In a quite analogous way we can interpret P

(x/y) as the probability

of ﬁnding a quark around a gluon.

The splitting functions P

and P

therefore describe the probability of

ﬁnding a gluon around a quark or gluon, respectively, and, accordingly, they

contribute to the gluon density G(x, t).

See also, G. Altarelli: Partons in Quantum Chromodynamics, Phys. Rep. C 81,1.

264 5. Perturbative QCD I: Deep Inelastic Scattering

However, it should be clear by now that the GLAP equations are an approx-

imation, valid only for large Q

and sufﬁciently large x. The ﬁrst condition is

obvious, since the GLAP equations are a perturbative expansion that becomes

rather meaningless for too large α

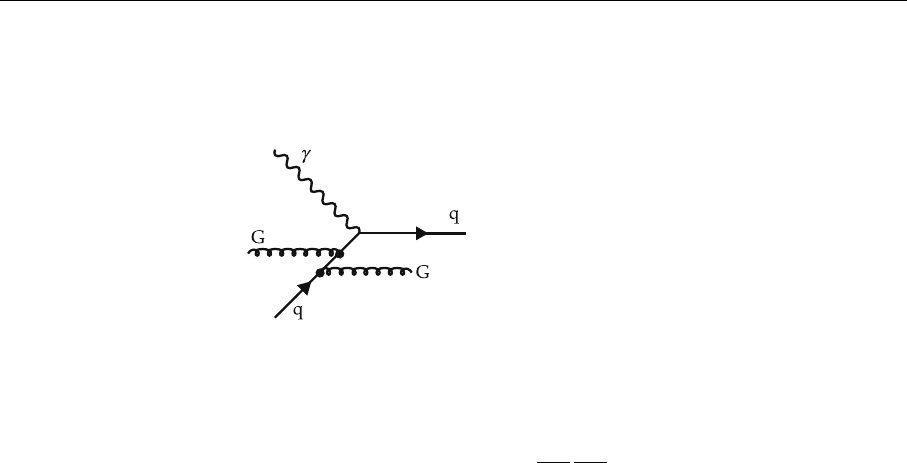
. Note, for example, the following process:

It represents a higher-order correction to the processes in Fig. 5.1; not one

bremsstrahlung gluon is involved (as in Fig. 5.1) but two. Therefore it contributes

to P

and P

in proportion to

G(x

)q(x

)

, x

, x)

, (5.73)

with a corresponding function

. This equation describes recombination ef-

fects. At very small x, not only bremsstrahlung processes occur, which are

described by the GLAP equations and one typical type of splitting function.

In the GLAP equation, one parent parton radiates a daughter parton and the

corresponding splitting function depends only on the ratio of the corresponding

momenta. If we want to treat recombination effects we have to introduce more

complicated “splitting functions”, which depend on three momenta: one parent

parton, one radiated “daughter” parton, and an additional absorbed gluon from

the surrounding gluon bath. Therefore one gets a type of equation which repre-

sents a convolution of the gluon bath structure function G(x

), the parent quark

q(x

), and a complicated recombination splitting function

, x

, x).The

structure function G(x

) and the splitting function

, x

, x) are difﬁcult to

determine. We shall not follow up this any further here.

The essential point now is the following: In the case of very small x

the

gluon distribution function G(x

) can increase so much that even α

G(x

) re-

mains larger than one (we shall ﬁnd later that G(x

) is proportional to 1/x

for

small x

). Hence there are kinematic regions where contributions like those of

Fig. 5.9 are no longer negligible. With the new HERA accelerator at DESY in

Hamburg, Germany, these regions have for the ﬁrst time become accessible to

experimental investigations. At HERA, an electron beam and a proton beam are

collided with an invariant mass of

s = ( p

+ p

)

≈ 4E

≈ 10

GeV

. (5.74)

Since the maximum momentum transfer ν

max

is just s/2, events with Q

≥

5GeV

and x ≥ 10

−4

can be investigated (see Exercise 5.4). Currently much ef-

fort is being invested in the necessary generalizations of the GLAP equations for

5.2 An Alternative Approach to the GLAP Equations 265

small values of x. To this end their structure must be modiﬁed, as can already

be seen from (5.73). Terms have to be introduced, for example, that depend on

products of two or more distribution functions. Up to now there has been no gen-

erally accepted solution to this problem (Sect. 6.2). Presumably such a solution

will only be found in connection with experimental investigations. The HERA

experiments have been producing data since 1992.

In this section we have learned how QCD corrections can be evaluated from

the corresponding Feynman graphs. This procedure is of great clarity, but it re-

quires extensive calculations. Therefore one frequently chooses another way to

derive the GLAP equations that is much more elegant but unfortunately less ob-

vious. The latter disadvantage occurs because a part of the result, namely the

general structure of the GLAP equations, has to be more or less assumed. We

shall discuss this alternative derivation in the following section, because it will

shed additional light on the meaning of the GLAP equations.

5.2 An Alternative Approach to the GLAP Equations

In this section we shall be concerned with the derivation of the GLAP equations

using only our knowledge about the properties of QCD.

We know already that

scattering experiments using leptons as projectiles and hadrons as targets reveal

information about the hadronic structure. The structure functions or momentum

distributions of the partons inside the hadron depend on the four-momentum q

carried by the exchanged photon (in general the vector meson). If the momentum

transfer Q

is increased, more and more details of the hadronic structure become

visible (see Fig. 5.10).

boost

small

large

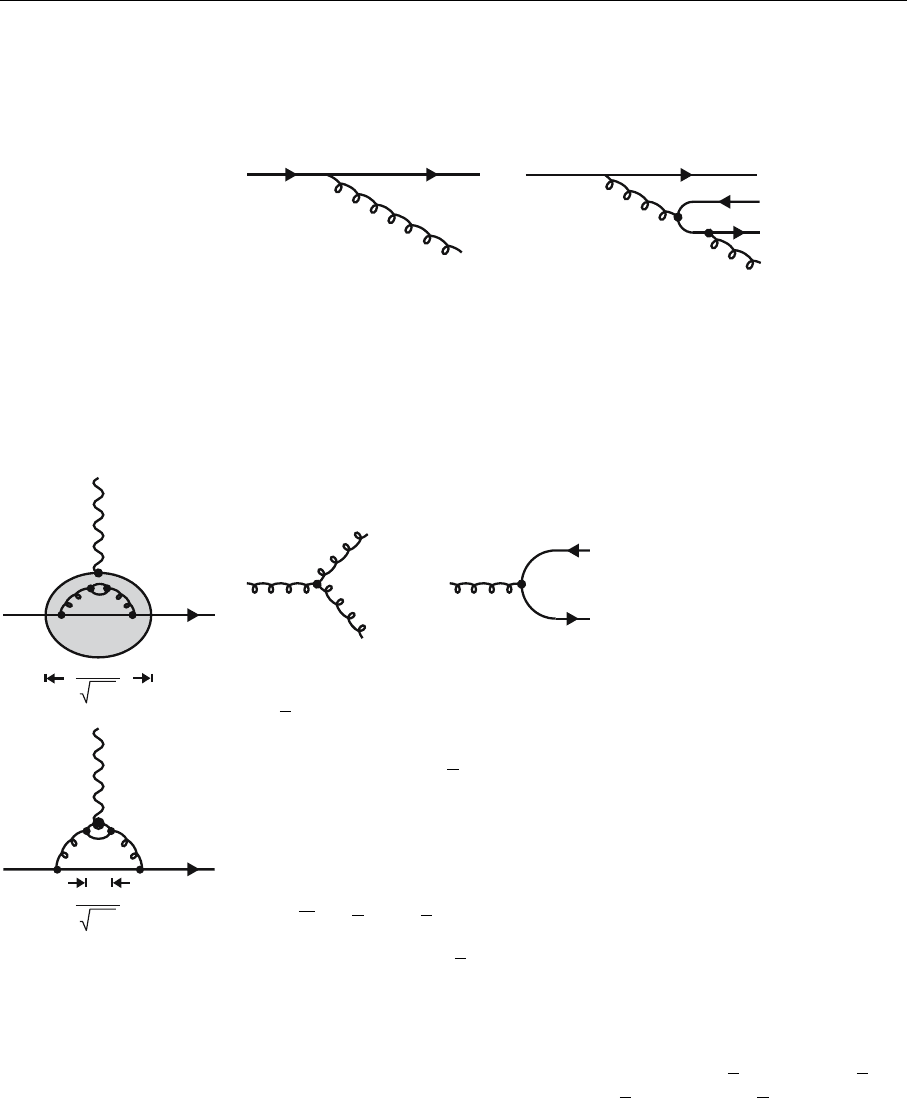
Fig. 5.10. TheroleofQ

transverse resolving power

is related to the maximum transverse momentum of a parton in the ﬁnal

state. This fact is easily understood by looking at Fig. 5.10. In the Breit frame,

where the distribution functions are deﬁned, the nucleon is strongly contracted in

the direction of movement. Therefore the resolution with which quarks are seen

depends only on the transverse momentum. We denote by 1/

the resolving

power, since hadronic structures down to 1/

can be resolved owing to the

Heisenberg inequality ∆x∆Q ∼ 1. Let us assume that we have chosen Q

high

enough to enter the perturbative regime. We can resolve partons of size 1/

inside the hadron. If the momentum transfer is increased to Q



> Q

, one can

O. Nachtmann: Elementary Particle Physics (Springer, Berlin, Heidelberg 1990).

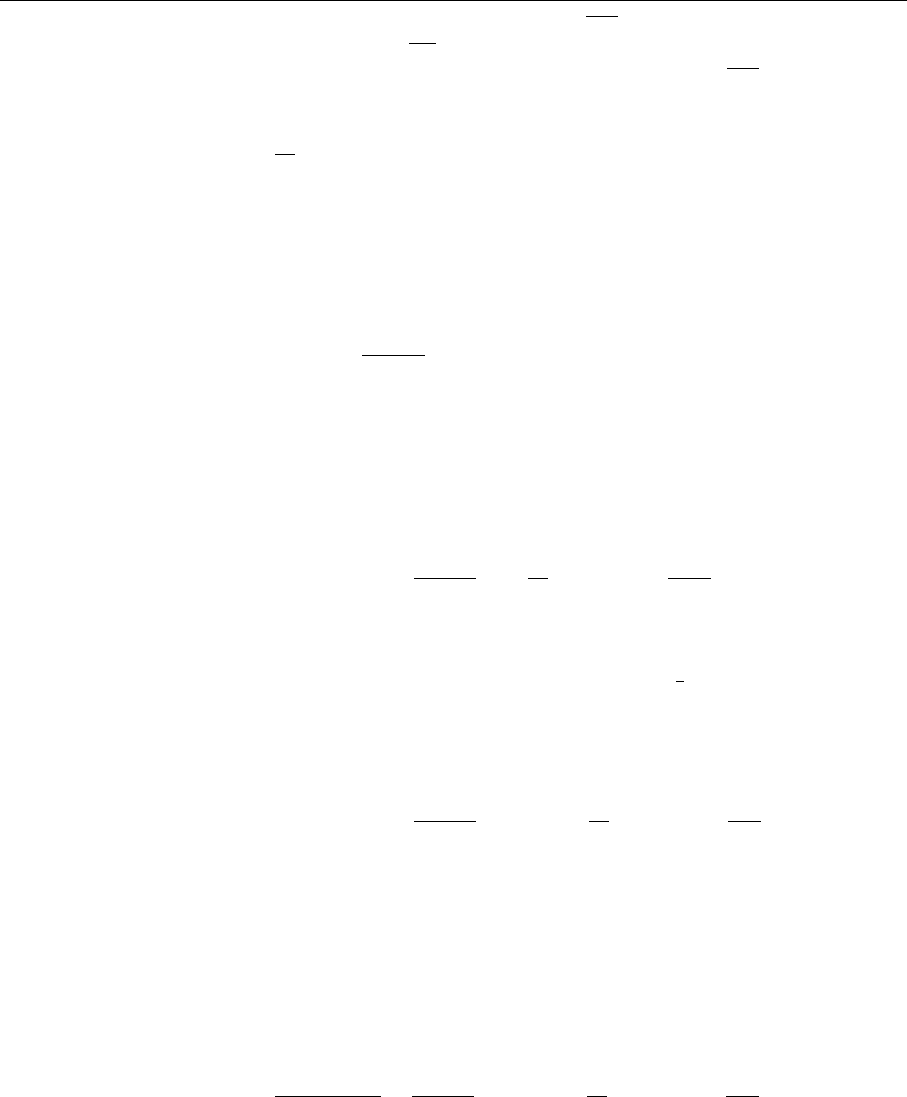
266 5. Perturbative QCD I: Deep Inelastic Scattering

resolve smaller constituents of size 1/



inside the hadron. For a given re-

solving power 1/

the momentum distribution of the partons of kind a is

denoted by N

, Q

). The smaller constituents b at 1/



carry some of the

parton momenta x

< 1 . (5.75)

This results in a decrease in the momentum distribution for large x and an in-

crease for small momentum fractions. In other words N

, Q

)<N

, Q

The variation of the distribution functions ∆N(x, Q

) when Q

is increased

by ∆Q

can now be treated by using perturbation theory. To lowest order,

∆N(x, Q

) is proportional to the coupling parameter

) =

)

4π

. (5.76)

If the quark masses are neglected, QCD lacks any energy scale. Therefore only

momentum ratios can appear that govern the development of N

, Q

) to

higher Q

. This distribution function for partons of kind a,i.e.N

, Q

),de-

pends for Q



> Q

on the distribution of partons of all kinds b. We assume this

dependence to be linear. The probability of ﬁnding a parton a with momentum

fraction x

inside a parton b of momentum fraction x

is therefore given by

∆N

, Q

) =

)





, Q

)

∆Q

. (5.77)

The quotient ∆Q

= ∆ ln Q

is introduced to keep the change in momen-

tum transfer dimensionless. In the same way it follows that P

can only depend

on the ratio of the momentum fractions. The factor

is convient.

To obtain the total change of N

we have to sum over all partons of kind a that

may “contain” the parton b, and we have to integrate over all parton momenta

> x

. This leads us, ﬁnally, to the GLAP equations:

∆N

, Q

) =

)

2π







, Q

)

∆ ln Q

. (5.78)

Here we have introduced the ratio dx

instead of dx

alone; otherwise a scale

would enter the GLAP equations. One might wonder why a dimensionless inte-

gration measure dx

does not appear in (5.75). However, remember, the also

dimensionless integration measure dx

/dx

would lead to a splitting function

with explicit dependence on single momenta and not only ratios. Equation (5.75)

describes a set of equations for all types of partons, which in differential form

becomes

∂N

, Q

)

∂ ln Q

)

2π







, Q

)

. (5.79)

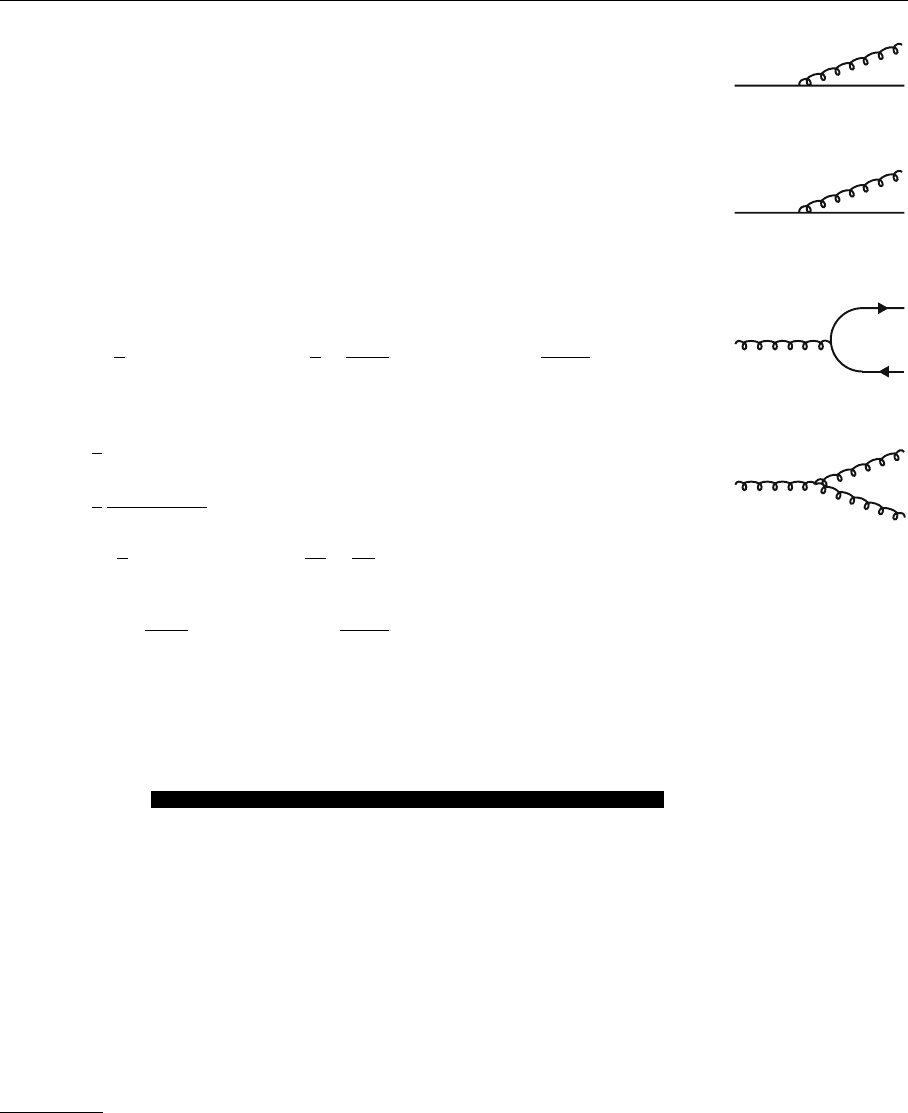
5.2 An Alternative Approach to the GLAP Equations 267

The functions P

are called s plitting fu nctions since they describe the breaking

up of a parton of type a into partons of type b, when the momentum transfer Q

is increased.

In the following we will derive the splitting functions P

for several cases.

Life is made easy by assuming that there are only two types of partons: quarks

and gluons. Since we assume that all antiquarks are due to gluon splitting,

G →

qq, the increase in the number of quarks always equals the increase in the

number of antiquarks. P

= P

=.... This is justiﬁed because

of charge-conjugation symmetry (change in quark distribution equals change in

antiquark distribution) and because of our treating quarks as massless objects

(changes in u, d, s quarks proceeds in the same way). This reduces the number

of splitting functions to four:

=−

(1 +x) +2δ(1 −x) +

⎛

⎝

1 −x

−δ(1 −x)



1 −x



⎞

⎠

(5.80)



(1 −x)



, (5.81)

1 +(1 −x)

, (5.82)



−2 +x(1 −x)





−



δ(1 −x)

⎛

⎝

1 −x

−δ(1 −x)



1 −x



⎞

⎠

. (5.83)

We shall evaluate the functions P

, P

,andP

in Examples 5.5–5.7. The

effect of these functions is depicted graphically in Fig. 5.11. The evaluation of

can be found in other papers.

EXERCISE

5.4 The Maximum Transverse Momentum

Problem. (a) Determine the maximum transverse momentum of a parton occur-

ring in the ﬁnal state if the photon momentum before the collision is given in the

Breit system (see Exercise 3.6) by

=(0;0, 0, −Q) (1)

and the initial parton momentum in the Breit system is

= ( p;0, 0, p). (2)

See also, G. Altarelli: Partons in Quantum Chromodynamics, Phys. Rep. C 81,1.

(a)

(b)

(c)

(d)

G,y

G,x-y

q,y

q,x-y

q,y

x-yq,

q,x

G,x

Fig. 5.11a–d. The processes

described by the splitting

functions (a) P

,(b) P

,and(d) P