Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

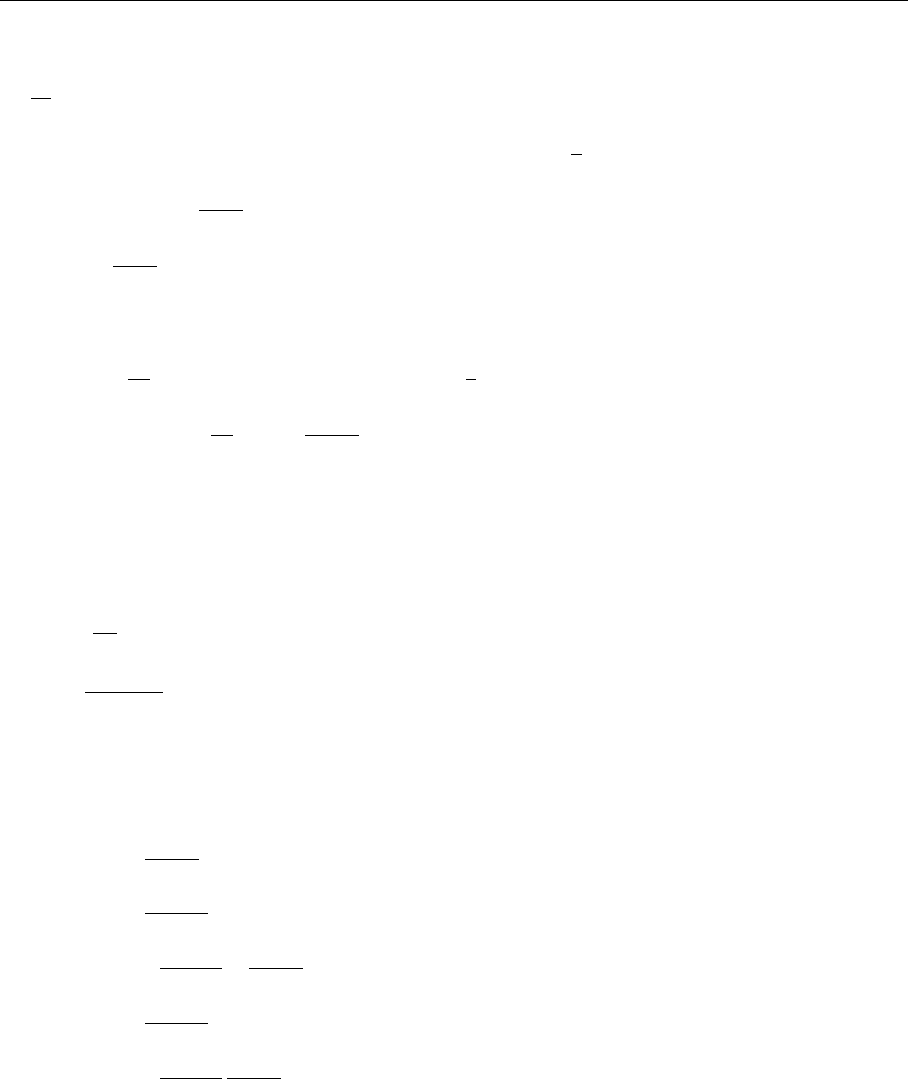
3.3 The MIT Bag Model 137
we get
d
dz
z
3
j
2
n
(z) − j
n−1
(z) j
n+1
(z)
=3z
2
j
2
n
(z) − j
n−1
(z) j
n+1
(z)
+z
3
2 j
n
(z)
− j
n+1
(z) +
n
z
j
n
(z)
− j
n−1
(z)
−
n +2
z
j
n+1
(z) + j
n
(z)
−
n −1
z
j
n−1
(z) − j
n
(z)
j
n+1
(z)
=3z
2
j
2
n
(z) − j
n−1
(z) j
n+1
(z)
+z
3
2n
z
j
2
n
(z) − j
n
(z)
j
n+1
(z) + j
n−1
(z)
+
3
z
j
n−1
(z) j
n+1
(z)
=3z
2
j
2
n
(z) +z
3
2n
z
j
2
n
(z) −
2n +1
z
j
2
n
(z)
=2z
2
j
2
n
(z). (13)
Terms of the form z
2
j
2
n
(z) appear in the integral (10). Therefore, relation (13)
allows a direct evaluation of that integral:
1 = N
2
R
3
2
j
2
κ
( pR) − j
κ
−1
( pR) j
κ
+1
( pR)
+
p
2
(E +m)
2
j
2
¯
κ
( pR) − j
¯
κ
−1
( pR) j
¯
κ
+1
( pR)
. (14)
Equation (14) can be simplified using (9). For κ<0wehave(see(12))
¯
κ
=
κ
+1 ,
κ
=−κ −1 ,
j
κ
+1
( pR) =
E +m
p
j
κ
( pR),
j
κ
−1
( pR) =
2
κ
+1
pR
j
κ
( pR) − j
κ
+1
( pR)
=
2
κ
+1
pR
−
E +m
p
j
κ
( pR),
j
κ
+2
( pR) =
2
κ
+3
pR
j
κ
+1
( pR) − j
κ
( pR)
=
2
κ
+3
pR
E +m
p
−1
j
κ
( pR). (15)
Exercise 3.11
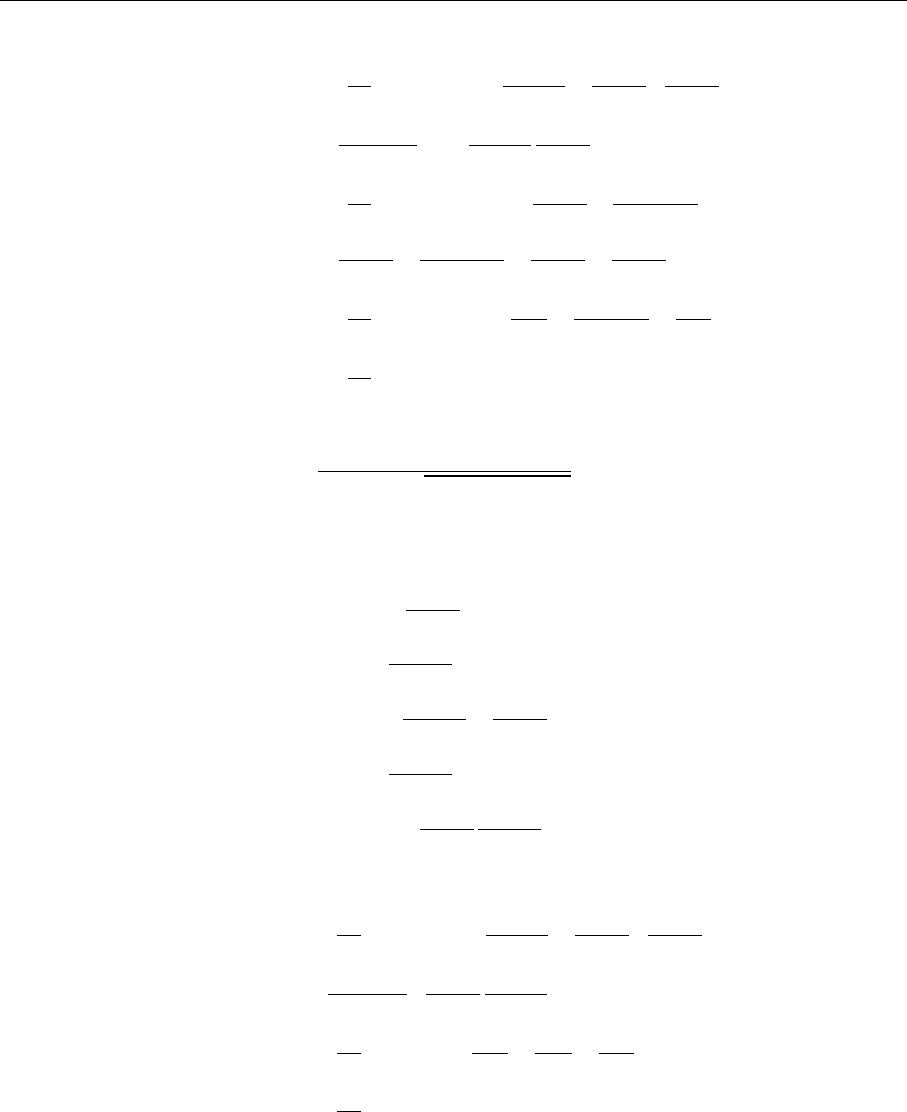
138 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.11
Equation (14) therefore becomes
1 = N
2
R
3
2
j
2
κ
( pR)
2 −
2
κ
+1
pR
−
E +m
p
E +m
p
+
p
2
(E +m)
2
1 −
2
κ
+3
pR
E +m
p
= N
2
R
3
2
j
2
κ
( pR)
2 −2
κ
E +m
p
2
R
+
1
(E +m)R
−
E +m
p
2
R
−
3
(E +m)R
+
E +m
E −m
+
E −m
E +m
= N
2
R
3
2
j
2
κ
( pR)
−2
κ
2E
p
2
R
−
4E −2m
p
2
R
+
4E
2
p
2
= N
2
R
2
p
2
j
2
κ
( pR)
2κE +m +2E
2
R
. (16)
Hence
N =
p
R|j
κ
( pr)|
√
2κE +m +2E
2
R
. (17)
For κ>0 an analogous calculation yields
¯
κ
=
κ
−1 ,
κ
= κ,
j
κ
−1
( pR) =−
E +m
p
j
κ
( pR),
j
κ
+1
( pR) =
2
κ
+1
pR
j
κ
( pR) − j
κ
−1
( pR)
=
2
κ
+1
pR
+
E +m
p
j
κ
( pR),
j
κ
−2
( pR) =
2
κ
−1
pR
j
κ
−1
( pR) − j
κ
( pR)
=−
E +m
p
2
κ
−1
pR
+1
j
κ
( pR). (18)
Equation (14) now has the form
1 = N
2
R
3
2
j
2
κ
( pr)
2 +
2
κ
+1
pR
+
E +m
p
E +m
p
+
p
2
(E +m)
2
E +m
p
2
κ
−1
pR
+1
= N
2
R
3
2
j
2
κ
( pr)
2
κ
2E
p
2
R
+
2m
p
2
R
+
4E
2
p
2
= N
2
R
2
p
2
j
2
κ
( pr)
2κE +m +2E
2
R
. (19)

3.3 The MIT Bag Model 139
Therefore N is given by (17) also for κ>0. The corresponding normaliza-
tion factors for massless quarks are obtained by setting p = E and m = 0, i.e.
N
κ
(m = 0) =
E
R
|
j
lκ
(ER)
|
1
√
2E(κ+ER)
(see also (3.142)).
Even in the simplest case, however, (3.143) leads to difficulties. From this equa-
tion a nucleon (three almost massless quarks in the ground state) and a pion (one
quark and one antiquark) should have almost the same radius:
R
N
R
π
=
3
2
1/4
=1.107 . (3.144)
This can be translated by (3.143) and (3.130) into a ratio of masses
M
N
M
π
=
3 ·2.043/R
N
2 ·2.043R
π
=
3
2
2
3
(1/4)
= 1.36 .
This result does not agree with physical reality. The prediction for the pion
mass is correspondingly much too large. In order to obtain a more realistic model
we therefore have to go beyond the simple assumptions made so far. Before
turning to applications of the MIT bag model, we want to discuss the necessary
additional assumptions. The main problem is the nonphysical equation (3.133).
It can be changed by introducing additional pressure terms with different R de-
pendence. Let us first consider the total energy, where the effect of these new
terms can be seen most clearly. So far the total energy consists of two terms: the
volume energy due to the external pressure B and the single-particle energies,
i.e.
E = B
4π
3
R
3
+
q
ω
q
R
,ω
q
= E
q
R = const . (3.145)
For
q
ω
q
−→ N
q
ω
q
we immediately recognize that a variation with respect
to R leads to (3.143). The first term added is
E
0
=−
Z
R
, Z = const . (3.146)
Equation (3.143) then assumes the form
R
4
=
N
q
ω
q
−Z
4πB
. (3.147)
A sufficiently large value of Z therefore allows us to adjust the mass and radius
difference between mesons and baryons. Physically this new term is interpreted
as the Casimir energy.
15
The bag yields a lower bound for the zero-point en-
ergy of the gluon field. The smaller the bag, the bigger the zero-point energy
15
See G. Plunien, B. Müller, and W. Greiner: Phys. Rep. 134, 87 (1986), see also
W. Greiner: Quantum Mechanics – Special Chapters (Springer, Berlin, Heidelberg
1998).
Exercise 3.11

140 3. Scattering Reactions and the Internal Structure of Baryons
of the vacuum oscillations. It is therefore clear that E
0
vanishes for R →∞
and diverges for R → 0. For very small values of R, however, the bag boundary
condition no longer makes any sense, because it is only an effective descrip-
tion of very complicated microscopic processes. Hence R must not assume
values smaller than the typical length scale of the reactions considered. If the
typical energies become larger than ∼1GeV
2
we have to apply perturbative
QCD, which models the interaction between quarks and gluons. Individual
quark–gluon interactions cannot be described by simple boundary conditions.
Therefore R < 1/Q should not become smaller than 0.2 fm. Strictly speaking,
we know neither the explicit functional form nor the sign of E
0
. The results of
simple model calculations do not justify (3.136) and are, in addition, completely
unreliable, since the self-interaction of the gluons (i.e., the non-Abelian structure
of QCD, see Chap. 4) has only been treated in a rough approximation. Equation
(3.136) should therefore be considered a phenomenological correction term with
unknown physical origin.
The next problem is to describe the mass splitting within the baryon multiplet.
Since all strange particles are considerable heavier than those with strangeness
S = 0, the introduction of quark masses seems to be a reasonable first step.
Therefore in the following we make use of the massive eigenfunctions and the
corresponding energy eigenvalues derived in Exercise 3.11. The masses of u, d,
and s quarks are treated as free parameters. This generalization, however, is not
sufficient to describe both the relatively small splitting between Σ and N and the
huge splitting between K and π. A further correction is necessary that assumes
different values for mesons and baryons. We therefore introduce the following
interaction between the quarks (see Example 3.12):
E
qG
= α
c
N ·
i< j
(σ
i
·σ
j
)
µ
i
µ
j
R
3
⎛
⎝
1 +2
R
0
dr
r
4
µ
i
µ
j
⎞
⎠
(3.148)
with
N =
)
2 for a baryon
4 for a meson
.
µ
i
and α
c
denote the magnetic moment of the quark with index i and the coupling
constant of the color interaction, respectively.
Equation (3.148) is obtained by taking the color magnetic interaction be-
tween the quarks into account. For a more detailed treatment of these matters we
refer to Chap. 4, where the QCD equations are discussed. At this point it need
only be mentioned that the derivation of (3.148) is not consistent. Again the glu-
onic self-interaction has been neglected. The electric and magnetic parts of the
remaining interaction (which then look exactly like the electromagnetic interac-
tion) are treated in a different way. In order to justify (3.148) we must therefore
postulate that all contributions except the one-gluon exchange are described by
the bag boundary condition. Since α
c
is treated more or less as a free parame-
ter (within certain limits), (3.148) can also be interpreted as a phenomenological

3.3 The MIT Bag Model 141
Fig. 3.15. The MIT-bag-
model fit for the lightest
mesons and baryons (from P.
Hasenfratz and J. Kuti: The
Quark Bag Model, Phys.
Rep. 40, 75 (1978))
correction. Summarizing the above arguments we find that the total energy
assumes the form
E =
4π
3
R
3
B +
q
ω
q
−Z
R
+E
qG
. (3.149)
The bag radius is determined by finding the minimum of E(R):
∂E
∂R
= 0 ,
∂
2
E
∂R
2
> 0 ⇒ R , (3.150)
and all features of the specific bags can be obtained by using the wave functions
introduced in Exercise 3.11.
A total of about 25 to 30 experimentally observed values for masses, mag-
netic moments, averaged charge radii, axial coupling constants, and so on is
available for fitting the six parameters B, Z, α
c
, m
s
, m
u
,andm
d
. The agreement
achieved in such a fit is in general better than 30%.
Let us start with the masses. Figure 3.15 depicts both the theoretical and the
experimental values for the following set of parameters:
16
B = (146 MeV)
4
, Z = 1.84 ,α
c
=2.2 ,
m
u
= 0MeV , m
d
= 0MeV , m
s
= 279 MeV . (3.151)
16
See T. De Grand, R.L. Jaffe, K. Johnson, J. Kiskis: Phys. Rev. D 12, 2060 (1975).

142 3. Scattering Reactions and the Internal Structure of Baryons
Clearly all the masses except that of the pion are quite well described. In gen-
eral the modified MIT model just described provides a satisfactory description
of the light hadrons except for the pion. One possible way out of this dilemma
is a combination of the bag model with a specific treatment of the pions. But we
are not going to discuss these so-called hybrid bag models.
Instead we evaluate the averaged charge radius and the magnetic moment of
the proton within the context of the MIT bag model. The squared charge radius
is defined as
r
2
ch
=
1
e
d
3
r
1
d
3
r
2
d
3
r
3
Ψ
†
p
ˆ
Q
ˆ
r
2
Ψ
p
. (3.152)
Here Ψ
p
denotes the proton wave function, which can be decomposed into quark
wave functions as follows
17
:
Ψ
p
m
s
=
1
2
=
1
3
√
2
2u
↑
(1)u
↑
(2)d
↓
(3) −u
↑
(1)u
↓
(2)d
↑
(3)
−u
↓
(1)u
↑
(2)d
↑
(3) −u
↑
(1)d
↑
(2)u
↓
(3) +u
↑
(1)2d
↓
(2)u
↑
(3)
−u
↓
(1)d
↑
(2)u
↑
(3) −d
↑
(1)u
↑
(2)d
↓
(3)
−d
↑
(1)u
↓
(2)d
↑
(3) +2d
↓
(1)u
↑
(2)d
↑
(3)
. (3.153)
u
↑
(1) denotes the wave function of a u quark with spin projection m
s
=+1/2
attached to quark number one. Inserting (3.153) into (3.152) and employing the
quark wave functions (3.128) (owing to (3.151), the up and down quarks are
assumed to be massless) leads to (see Exercise 3.13)
r
2
ch
= 0.53 R
2
. (3.154)
The bag radius R follows by minimizing (3.149), yielding R = 1fm (the param-
eters have been correspondingly adjusted). Hence
r
2
ch
= 0.73 fm , (3.155)
which agrees with the experimental value to within 20%:
r
2
(exp) = 0.88 ±0.03 fm . (3.156)
The magnetic moment is obtained by evaluating the expectation value of the
corresponding operator:
ˆ
µ =
ˆ
Q
2
ˆ
r ×
ˆ
α , (3.157)
µ
p
=
d
3
r
1
d
3
r
2
d
3
r
3
Ψ
†
p
i
ˆ
Q
i
2
ˆ
r
i
×
ˆ
α
i
Ψ
p
. (3.158)
17
See also W. Greiner and B. Müller: Quantum Mechanics – Symmetries, 2nd ed.,
(Springer, Berlin, Heidelberg 1994), P. Hasenfratz, J. Kuti, Phys. Rep. 40 C,75
(1978).

3.3 The MIT Bag Model 143
We again insert the wave functions (3.153) and (3.128). A detailed calculation,
which will be performed in Exercise 3.14, yields
µ
p
µ
K
=1.9 , (3.159)
where µ
0
=e/2m
p
denotes the nuclear magneton and m
p
is the proton mass.
EXAMPLE
3.12 Gluonic Corrections to the MIT Bag Model
Although the general structure of hadrons, i.e. the masses of baryons, are rather
well described in the framework of the simple bag model of noninteracting
quarks, the mass splitting in the baryon multiplett cannot be accounted for
properly.
We will study the quark interaction energy due to their coupling to colored
gluons. The interaction will be calculated only to lowest order in α
s
= g
2
/4π.
The appropriate diagrams are given in Fig. 3.16.
The gluon interaction will lift the spin degeneracies of the simple model,
splitting the nucleon from the ∆ resonance, and the from the π.
To lowest order in α
s
the non-Abelian gluon self-coupling does not contribute
and the gluons act as eight independent Abelian fields.
Calculating the color field, therefore, is equivalent to finding the solution of
the classical Maxwell equations under the bag boundary conditions
n ·
i
E
A
i
= 0 , (1a)
n ×
i
B
A
i
=0 , (1b)
where the index i refers to the number of quarks in the bag. The index A de-
notes color and runs from 1 to 8. E
A
and B
A
are gluon electric and magnetic
field components. These boundary conditions are necessary to confine the glu-
ons to the bag. The electrostatic interaction energy of a static charge distribution
i is
∆E
E
=
1
2
i, j
d
3
r E
A
i
·E
A
j
. (2)
Similarly, the magnetostatic interaction energy is
∆E
µ
=−
1
2
i, j
d
3
r B
A
i
·B
A
j
. (3)
E
A
and B
A
are determined from the quark charge and current distributions by
Maxwell’s equation and the boundary conditions (1a) and (1b). The terms with
Fig. 3.16a,b. Lowest-order
gluon interaction diagram
for a baryon. Mesons are
similar. (a) Gluon exchange;
(b) gluon self energy

144 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.12
i = j are due to the self-energy diagram in Fig. 3.16b. These diagrams contribute
to a renormalization of the quark mass. A proper treatment would separate this
contribution of renormalization from the rest of Fig. 3.16b, since its effect is
already included in the phenomenological quark mass one uses.
To avoid double counting, one usually neglects the self-energy contribution
for the calculation of the magnetic energies, whereas it is taken into account in
the calculation of the electric energies.
Equation (3) therefore may be rewritten as
∆E
µ
=−g
2
i, j
d
3
r B
A
i
·B
A
j
. (4)
The color magnetic field must satisfy
∇ ×B
A
i
= j
A
i
, r < R ,
∇ ·B
A
i
=0, r < R ,
n ×
i
B
i
= 0, r = R, (5)
where j
A
i
is the color current of quark i:
j
A
i
=q
†
i
α
λ
A
2
q
i
=−
3
8π
e
r
×σ
i
λ
A
i
µ
i
(r)
r
3
. (6)
Here µ
i
(r) is the scalar magnetization density of a quark of mass m
i
in the lowest
cavity eigenstate:
µ
i
(m
i
, R) =
⎛
⎜
⎝
1
2
V
B
q
†
i
(r)(r ×α)q
i
(r)
⎞
⎟
⎠
z
d
3
r =
R
0
d rµ
i
(r). (7)
The integral over µ
i
(r) yields the magnetic moment of quark i.
Equation (5) may be integrated to determine B
A
i
(r):
B
A
i
(r) =
1
8π
λ
A
i
σ
i
2M
i
(r) +µ(m
i
, R)/R
3
−µ(m
i
, r )/r
3
+
3
8π
λ
A
i
e
r
(e
r
·σ
i
)µ(m
i
, r )/r
3
(8)
with
M
i
(r) =
R
r
µ
i
(r
)d r
. (9)

3.3 The MIT Bag Model 145
Inserting (8) into (4) yields
∆E
µ
=−
3
4
α
s
i, j
(σ
i
λ
A
i
)(σ
j
λ
A
j
)µ(m
i
, R)µ(m
j
, R)/R
3
×
⎛
⎝
1 +2
R
0
drµ(m
i
, R)µ(m
j
, R)/r
4
⎞
⎠
. (10)
The colour and spin dependences of (10) may be simplified considerably. For
a colour-singlet meson
λ
A
1
λ
A
2
|M=0 (11)
we find, after squaring,
A
(λ
A
i
)
2
= 16/3 (12)
and therefore
A
λ
A
1
λ
A
2
=−16/3.
Likewise for baryons
3
i=1
λ
A
i
|B=0 (13)
and accordingly
A
λ
A
i
λ
A
j
=−8/3, i = j . (14)
The final expression for the magnetic interaction energy is
∆E
µ
= Nα
s
i=j
(σ
i
·σ
j
)µ(m
i
, R)µ(m
j
, R)/R
3
×
⎛
⎝
1 +2
R
0
drµ(m
i
, R)µ(m
j
, R)/r
4
⎞
⎠
, (15)
where N =2 for a baryon and N = 4 for a meson. For a nucleon (three massless
1s
1/2
quarks) one gets
∆E
N
µ
≈−3.5
α
s
R
. (16)
The gluon electrostatic energy can be calculated along the same line. The color
electric field for a single quark must satisfy
∇ ·E
A
i
= j
0A
i
, r < R (17a)
∇ ×E
A
i
=0, r < R (17b)
i
n ·E
A
i
= 0, r = R , (17c)
Example 3.12

146 3. Scattering Reactions and the Internal Structure of Baryons
Example 3.12
where j
0A
i
(r) is a single quarks’ color charge density
j
0A
i
=q
†
i
λ
A
2
q
i
=
λ
A
8πr
2
i
(r). (18)
Here
i
(r) is the charge density of a quark of mass m
i
in the lowest cavity
eigenmode and satisfies
R
0
dr
i
(r
) = 1 . (19)
The color electric field is obtained from Gauss’ law:
E
A
i
=
λ
A
8πr
2
e
r
i
(r), (20)
where
i
(r) is the integral over
i
(r) out to a given radius r.
Now if all of the quarks in a given hadron have the same mass, then
i
(r) is
independent of the index i and the total color electric field is given by
E
A
=
e
r
8πr
2
(r)
i
λ
A
i
. (21)
For a color-singlet hadron,
λ
A
|H=0. Therefore E
A
= 0. From (2) we see
that ∆E
E
= 0. Notice that it was essential to include the static self-interaction
(E
A
i
·E
A
i
) to obtain this correlation. In this approximation the energy shift in the
baryon multiplett due to gluonic interaction is entirely attributed to the magnetic
interaction.
EXERCISE
3.13 The Mean Charge Radius of the Proton
Problem. Evaluate the right-hand side of (3.142):
r
2
ch
=
1
e
d
3
r
1
d
3
r
2
d
3
r
3
Ψ
†
p
(
ˆ
Qr
2
)Ψ
p
. (1)
Solution. Sincer
2
does not change the quantum number m
s
, all spin orientations
yield the same value. Therefore we can restrict our calculation to one specific
case,
Ψ
p
m
s
=
1
2
→
1
√
6
2u
↑
(1)u
↑
(2)d
↓
(3)
−u
↑
(1)d
↑
(2)u
↓
(3) −d
↑
(1)u
↑
(2)u
↓
(3)
. (2)
