Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

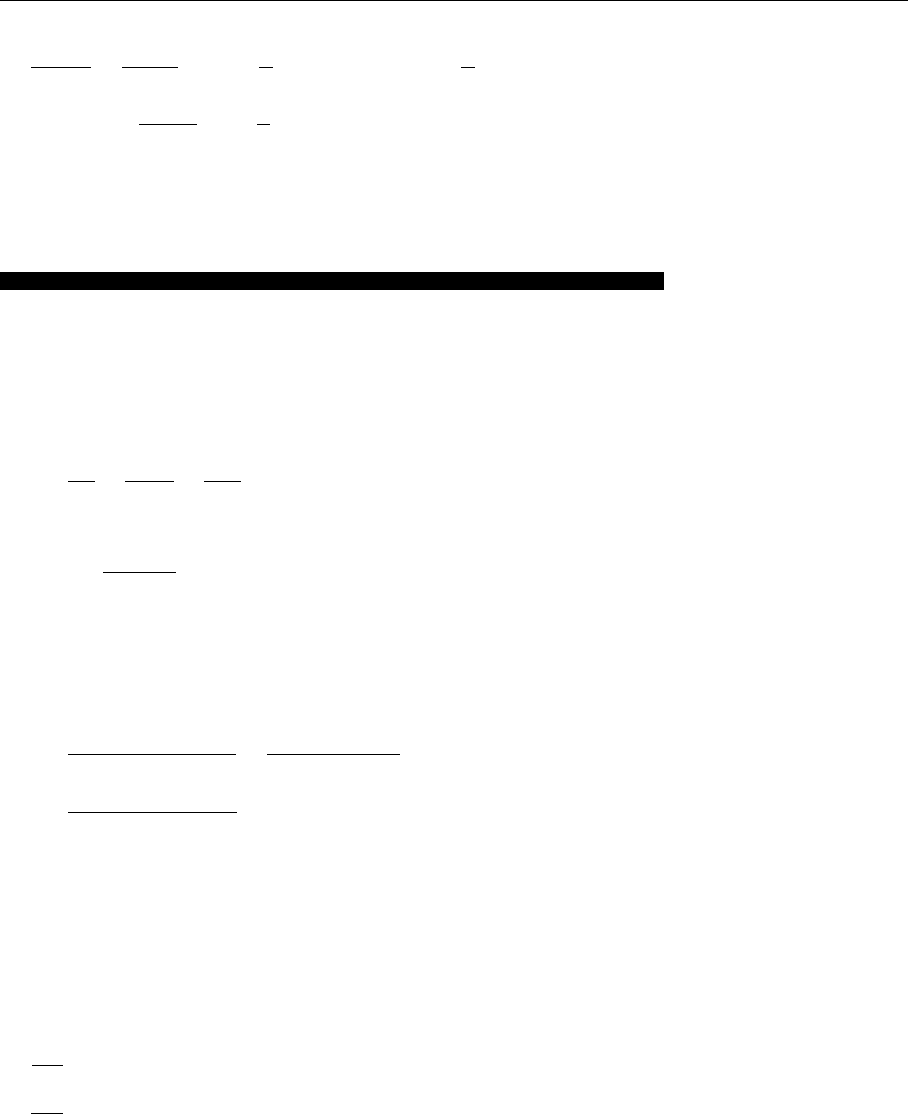
3.2 The Description of Scattering Reactions 97
d
2
σ
dE
dΩ
=
G
2
F
E
2
2π
2
2sin
2
ϑ
2
W
1
(Q
2
,ν)+cos
2
ϑ
2
W
2
(Q
2
,ν)
−
E +E
M
N
sin
2
ϑ
2
W
3
(Q
2
,ν)
. (17)
This is identical to (3.37). In the reaction
¯
ν +N →e
+
+X the incoming antineu-
trino corresponds to the outgoing electron in the reaction ν +N →e
−
+X, i.e.,
p and p
are exchanged. Since the third term in L
µν
is antisymmetric under this
exchange, the sign of W
3
changes.
We shall now discuss the experimental structure functions of electron–
nucleon scattering. These functions will have a particularly simple form when
ν is replaced by x = Q
2
/2ν. This quantity is called the Bjorken or scaling vari-
able. We shall first consider some of its properties. For elastic scattering, (3.19)
and (3.7) give
x =
Q
2
2ν
=
−q
2
2P ·q
=
−q
2
−q
2
= 1 . (3.39)
Since the nucleon is the lightest state with baryon number 1, we know in addition
that the invariant mass of the final state
M
X
=
(P +q)
2
(3.40)
must be larger than M
N
. If this were not the case, there would be a state X (of
arbitrary structure) with baryon number 1 into which the proton could decay, by
emitting γ quanta, for example.
From (3.40) it follows that x is always positive and less than 1:
x =
Q
2
(P +q)
2
− P
2
+Q
2
=
Q
2
M
2
X
−M
2
N
+Q
2
=
1
1 +(M
2
X
−M
2
N
)/Q
2
; (3.41)
Q
2
is always positive, as can be seen from (3.30), and
0 < x ≤ 1 . (3.42)
Additionally, it is customary to include a factor of ν in the definition of W
2
and
W
3
and a factor of M
N
in the definition of W
1
. Thus we are lead to “new” form
factors F
1
, F
2
, F
3
instead of W
1
, W
2
,andW
3
, respectively:
M
N
W
eN
1
(Q
2
,ν)= F
eN
1
(Q
2
, x),
ν
M
N
W
eN
2
(Q
2
,ν)= F
eN
2
(Q
2
, x),
ν
M
N
W
νN
3
(Q
2
,ν)= F
eN
3
(Q
2
, x). (3.43)
Exercise 3.4
98 3. Scattering Reactions and the Internal Structure of Baryons
Fig. 3.4. The physical mean-
ing of the different domains
of x, Q
2
,andν. Q
2
=2M
ν
holds for elastic scattering
only, otherwise Q
2
and ν are
independent
Frequently, also the parameter Q
2
is replaced by a new quantity, the inelasticity
parameter y:
y =
ν
M
N
E
=
E −E
E
. (3.44)
y is dimensionless and specifies which fraction of the lepton energy in the labo-
ratory system is transferred to the nucleon. The value of y thus lies in the range
0 ≤ y ≤ 1. The meaning of Q
2
, ν,andx is also illustrated in Fig. 3.4. It can easily
be checked (see Exercise 3.5) that
d
2
σ
dE
dΩ
=
E
2πM
N
Ey
d
2
σ
dxdy
. (3.45)
In this notation, (3.32) becomes (see Exercise 3.5):
d
2
σ
dx dy
eN
=
8πM
N
Eα
2
Q
4
×
xy
2
F
eN
1
(Q
2
, x) +
1 − y −
M
N
xy
2E
F
eN
2
(Q
2
, x)
. (3.46)
The first measurements of inelastic electron–proton scattering at high energies
were performed in 1968 at the Stanford Linear Accelerator (SLAC). These and
subsequent experiments have yielded two important results:
(1) For sufficiently large values of Q
2
, i.e., for Q
2
≥1GeV
2
, F
eN
2
and F
eN
1
do
not depend significantly on Q
2
, but only on x.ThisbehavioristermedBjorken
scaling.
(2) In this domain (i.e., for Q
2
≥ 1GeV
2
) it holds to good approximation that
F
eN
2
≈2xF
eN
1
.
3.2 The Description of Scattering Reactions 99
EXERCISE
3.5 The Cross Section as a Function of x and y
Problem. Derive (3.45) and (3.46).
Solution. Equations (3.44), (3.39), and (3.30) yield
y =
E −E
E
= 1 −
E
E
,
x =
Q
2
2(E −E
)M
N
=
2EE
(E −E
)M
N
sin
2
θ
2
. (1)
Owing to the cylindrical symmetry of the problem we have in addition
d
2
σ
dE
dΩ
=
d
2
σ
dE
2π sin(θ)dθ
. (2)
Therefore we only have to evaluate the Jacobi determinant
d
2
σ
dE
dΩ
=
1
2π sin(θ)
∂(x, y)
∂(E
,θ)
d
2
σ
dxdy
=
2E sin
2
θ
2
M
N
E
+(E−E
)
(E−E
)
2
2EE
(E−E
)M
N
sin
θ
2
cos
θ
2
−
1
E
0
1
2π sin(θ)
d
2
σ
dxdy
=
1
2π sin(θ)
2E
(E −E
)M
N
sin(θ)
2
d
2
σ
dx dy
=
E
2πM
N
Ey
d
2
σ
dx dy
. (3)
This is identical to (3.45). With the help of the definitions introduced in (3.39)–
(3.44) the double-differential cross section for electron–nucleon scattering con-
sequently becomes
d
2
σ
dxdy
=
8πM
N
yE E
α
2
Q
4
2
M
N
sin
2
θ
2
F
eN
1
(Q
2
, x)+
cos
2
θ
2
yE
F
eN
2
(Q
2
, x)
.
(4)
Here we have employed (3.32) and (3.43). Now we replace θ by x and y,
using (1):
sin
2
θ
2
=
(E −E
)M
N
2EE
x =
M
N
2E
xy , (5)

100 3. Scattering Reactions and the Internal Structure of Baryons
Exercise 3.5
Fig. 3.5. The F
2
struc-
ture functions for electron–
proton and electron–neutron
scattering have been com-
bined into F
ep
2
±F
en
2
and
plotted against Q
2
.The
Bjorken variable x is defined
as x = Q
2
/2νM
N
(see Re-
view of Particle Properties:
Phys. Lett. 170 (1986))
d
2
σ
dxdy
=
8πM
N
yE E
α
2
Q
4
xy
E
F
eN
1
(Q
2
, x) +
1 −
M
N
2E
xy
yE
F
eN
2
(Q
2
, x)
=
8πM
N
Eα
2
Q
4
xy
2
F
eN
1
(Q
2
, x) +
1 − y −
M
N
2E
xy
F
eN
2
(Q
2
, x)
,
(6)
which yields (3.46).
These results are illustrated in Figs. 3.5 and 3.6. In Fig. 3.5 it can be seen that,
at least for medium values of x, the measured points are practically horizontal. In
the following we shall discuss the physical meaning of this. In Chap. 5 we shall
discuss how the Q
2
dependence of the structure functions for large and small x
can be understood in the framework of quantum chromodynamics.
These two unusual properties can be easily reduced to the common physi-
cal cause that the scattering is off pointlike spin-
1
2
constituents of the nucleon.
These constituents are termed, following R.P. Feynman, partons.Whatdowe
know about this kind of scattering?
The scattering cross section dσ
i
/dΩ for the scattering of electrons off
a pointlike parton of mass M
i
and charge q
i
e can be constructed from the re-

3.2 The Description of Scattering Reactions 101
sults for electron–muon scattering, namely (2.173), (see in particular 11 in
Exercise 2.13), which now reads
dσ
i
dΩ
=
α
2
q
2
i
4E
2
sin
4
θ/2
E
E
cos
2
θ/2
1 −
q
2
tan
2
θ/2
2M
2
i
=
α
2
q
2
i
4E
2
E
E
1
sin
4
θ/2
'
cos
2
θ/2 +
Q
2
4M
2
i
sin
2
θ/2
(
.
From
2
E −E
M = 2ν = Q
2
=+4EE
sin
2
θ
2
,
one finds
E
E
=1 +
2E
M
sin
2
θ
2
,
and therefore
dσ
i
dΩ
=
α
2
q
2
i
4E
2
sin
4
θ
2
1
1 +
2E
M
i
sin
2
θ
2
cos
2
θ
2
'
1 −
q
2
tan
2
θ
2
2M
2
i
(
=
α
2
q
2
i
4E
2
1
sin
4
θ
2
cos
2
θ
2
−
q
2
2M
2
i
sin
2
θ
2
1 +
2E
M
i
sin
2
θ
2
. (3.47)
This cross section is computed in the laboratory system as the rest system of the
parton. The laboratory system, however, is quite unsuitable for our needs since
here partons cannot be treated as free particles because they are held together by
the interaction to which this volume is dedicated. Thus we do not know at all the
initial momenta of the partons; they are definitely not at rest. There are, however,
frames of reference where the initial momentum is known. These are all frames
of reference in which the nucleon is moving very fast. The momentum of the ith
parton is then
P
i,µ
=ξ
i
· P
µ
+∆P
iµ
, max
µ
(∆P
µ
) max
µ
(P
µ
). (3.48)
Here max
µ
(∆P
µ
) stands for the maximum of ∆P
µ
for the various space–time
components µ. The unknown momentum fraction ∆P
iµ
, which comes from the
interactions of the partons with each other, is much smaller than the momen-
tum from the collective motion. To describe electron–parton scattering sensibly,
(3.47) must be transformed into a different Lorentz system.
9
This is done by
rewriting it using only the invariant variables
( p − p
)
2
=: t =−Q
2
=(P − P
)
2
,
( p + P)
2
=: s = ( p
+ P
)
2
,
( p
− P)
2
=: u = ( p − P
)
2
. (3.49)
9
Here and in the following we omit the parton index i on the mass and momentum
variables.

102 3. Scattering Reactions and the Internal Structure of Baryons
These quantities are called Mandelstam variables. In the laboratory system
Q
2
= 4EE
sin
2
θ
2
, (3.50a)
s = 2 p · P + M
2
= M(2E +M), (3.50b)
u =−2 p
· P +M
2
=−M(2E
−M). (3.50c)
The small mass of the electron (m
2
M
2
, p · P) has been neglected here. Q
2
is
solely a function of θ, because the E
appearing in (3.50a) can be expressed in
terms of E and θ (see (3.53) below). Therefore we may use (note the cylindrical
symmetry)
dσ
dΩ
=
1
2π
dσ
sin(θ)dθ
=
1
2π sin(θ)
dQ
2
dθ
dσ
dQ
2
. (3.51)
From P
µ
= P
µ
+ p
µ
− p
µ
, it follows that
M
2
= P
2
µ
= (P
µ
+ p
µ
− p
µ
)
2
= M
2
+(2E −E
)M −Q
2
, (3.52)
or, after solving for E
,
E
= E
1 +2
E
M
sin
2
θ
2
−1
. (3.53)
For the derivative dQ
2
/dθ we obtain, with (3.50a) and (3.53),
dQ
2
dθ
= 4EE
sin
θ
2
cos
θ
2
−
E 2
E
M
sin
θ
2
cos
θ
2
1 +2
E
M
sin
2
θ
2
2
4E sin
2
θ
2
= 2EE
sin θ
)
1 −
2E sin
2
θ
2
M
1 +2
E
M
sin
2
θ
2
*
=
2EE
sin θ
1 +2
E
M
sin
2
θ
2
. (3.54)
For dσ/dQ
2
we therefore find according to (3.51) and (3.47) that
dσ
dQ
2
=
2π sin
2
dQ
2
dθ
dσ
dω
=
π
EE
α
2
q
2
i
4E
2
1
sin
4
θ
2
'
cos
2
θ
2
+
Q
2
2M
2
i
sin
2
θ
2
(
. (3.55)

3.2 The Description of Scattering Reactions 103
We further insert, according to (3.50),
E
=
u − M
2
i
−2M
i
, E =
s −M
2
i
2M
i
,
sin
2
θ
2
=
Q
2
4EE
=−
Q
2
M
2
i
u − M
2
s −M
2
i
,
cos
2
θ
2
= 1 +
Q
2
M
2
i
u − M
2
i
s −M
2
i
, (3.56)
so that after appropriate substitutions, (3.55) becomes
dσ
i
dQ
2
=
4πα
2
q
2
i
Q
4
×
−
u
i
−M
2
i
s
i
−M
2
i
'
1 +
1 −
Q
2
2M
2
i
Q
2
M
2
i
u
i
−M
2
i
s
i
−M
2
i
(
. (3.57)
The quantities u
i
and s
i
refer to the ith parton. With this, we have succeeded in
the first step. We must now choose an appropriate laboratory system and sub-
stitute the parton masses. It is now a major statement of the parton model that
one obtains a good description of experimental results when one assumes that
partons are massless.ForM
i
→0, (3.57) simplifies to
dσ
i
dQ
2
=
4πα
2
q
2
i
Q
4
Q
4
2u
i
s
i
−1
u
i
s
i
. (3.58a)
In addition, from (3.49) one deduces
Q
2
−s
i
−u
i
= 2p · p
−2 p · P
i
+2 p · P
i
= 2p ·( p
− P
i
+ P
i
) = 2p
2
=0 (3.59)
and therefore Q
4
=s
2
i
+u
2
i
+2u
i
s
i
,sothat
Q
4
2u
i
s
i
−1
u
i
s
i
=
s
2
i
+u
2
i
2s
2
i
. (3.60)
Thus (3.58a) becomes
dσ
i
dQ
2
=
4πα
2
q
2
i
Q
4
s
2
i
+u
2
i
2s
2
i
. (3.58b)
For our frame of reference, we now choose the so-called Breit system.This
is characterized by the property that q
µ
is purely spacelike and points in the
z direction (see Exercise 3.6):
q
µ
=
0, 0, 0,
−q
2
=
0, 0, 0,
"
Q
2
,
P
µ
=
˜
P, 0, 0, −
˜
P
,
˜
P M
N
, P
2
=
˜
P
2
−
˜
P
2
=0 ≈ M
2
N
. (3.61)
104 3. Scattering Reactions and the Internal Structure of Baryons
Since we neglect the momentum fraction of the partons stemming from the
parton–parton interaction, for consistency we must also neglect the nucleon
masses:
P
i,µ
= ξ
i
˜
P, 0, 0, −
˜
P
. (3.62)
The cross section for scattering off a parton in the Breit system thus becomes
dσ
i
dQ
2
=
4πα
2
q
2
i
Q
4
( p + P
i
)
4
+( p
− P
i
)
4
2(p + P
i
)
4
=
4πα
2
q
2
i
Q
4
(ξ
i
2p · P)
2
+(ξ
i
2p
· P)
2
2(2ξ
i
p · P)
2
=
4πα
2
q
2
i
Q
4
( p + P)
4
+( p
− P)
4
2(p + P)
4
=
4πα
2
q
2
i
Q
4
s
2
+u
2
2s
2
. (3.63)
s and u are now Mandelstam variables for the whole nucleon. We recognize that
dσ/dQ
2
is completely independent of ξ
i
. To compare this expression with (3.46),
we must write in the Breit system not only the elastic scattering cross section for
pointlike particles, i.e.(3.63) above, but also the inelastic scattering cross section
for particles with an internal structure (see (3.46)). To this end, (3.46) is rewrit-
ten such that only Lorentz-invariant quantities appear. For M
2
N
u, s, Q
2
(see
(3.56))
E
=−
u
2M
N
, E =
s
2M
N
,
y =
E −E
E
≡
s +u
s
(3.64)
and
x =
Q
2
2ν
=
Q
2
2P ·q
=
Q
2
s +u
. (3.65)
Equation (3.46) is thus nearly in invariant form. One only has to substitute s
for E:
d
2
σ
dx dy
eN
=
4πsα
2
Q
4
'
xy
2
F
eN
1
(Q
2
, x) +
1 − y −
xyM
2
N
s
F
eN
2
(Q
2
, x)
(
.
(3.66)
Because M
N
s the second term can be further simplified. This expression must
now be compared to the sum over partons i of (3.63). To this end, we must first
rewrite (3.63) as a double-differential cross section.
To do this, we start from the momentum conservation P
i
= P
i
+q for the
scattering parton, i.e.,
0 ≈ P
i
2
= (P
i
+q)
2
=(ξ
i
P +q)
2
=ξ
2
i
M
2
i
+2ξ
i
P ·q +q
2
. (3.67)
3.2 The Description of Scattering Reactions 105
When the parton mass vanishes, this implies that
ξ
i
=
Q
2
2P ·q
= x . (3.68)
This is an interesting relation, which allows us to interprete the variable x in
a new way: If we observe scattering characterized by a Bjorken variable x,this
means in the parton model that the interacting parton carried a fraction ξ
i
= x of
the nucleon’s total momentum! Hence the variable x has a simple meaning (but
only in reference frames with very large nucleon momentum, e.g. in the Breit
frame).
Owing to (3.68), (3.63) can immediately be written as a double differential:
d
2
σ
dx dQ
2
=
4πα
2
q
2
i
Q
4
s
2
+u
2
2s
2
δ(ξ
i
−x). (3.69)
The transition from Q
2
to the desired variable y is achieved with the aid of (3.39),
(3.44), and (3.56), according to which
Q
2
=2 P ·qx= 2M
N
(E −E
)x = 2M
N
Eyx =syx , (3.70)
and we thus obtain
d
2
σ
dx dy
=
dQ
2
dy
x
d
2
σ
dx dQ
2
=
2πα
2
q
2
i
Q
4
s
2
+u
2
s
2
δ(ξ
i
−x)
Q
2
s
s +u
. (3.71)
Here, in the last step, we have put x = Q
2
/(s +u), according to (3.65). To obtain
the total cross section in the parton model, we must sum (3.71) over all partons i
and all possible momentum fractions ξ
i
. The single terms of the sum must be
weighted with their proper probabilities f
i
(ξ
i
):
d
2
σ
dx dy
eN
=
i
1
0
dξ
i
f
i
(ξ
i
)
2πα
2
q
2
i
Q
4
s
2
+u
2
s
2
δ(ξ
i
−x)
Q
2
s
s +u
=
2πα
2
s
Q
4
s
2
+u
2
s
2
i
f
i
(x)q
2
i
x
remember x =
Q
2
s +u
=
2πα
2
s
Q
4
(y −1)
2
+1
i
f
i
(x)q
2
i
x (3.72)
with
(y −1)
2
+1 = y
2
−2y +2 =
s +u
s
2
−2
s +u
s
+2
=
s
2
+u
2
s
2
+
2su
s
2
−2
s +u
s
+2
=
s
2
+u
2
s
2
106 3. Scattering Reactions and the Internal Structure of Baryons
according to (3.64). For the momentum distribution functions f
i
(ξ
i
) of the
partons the normalization
1
0
dξ
i
f
i
(ξ
i
) = 1 (3.73)
holds. Comparing (3.72) with (3.66) shows that in the parton model the following
identification must hold:
2
xy
2
F
eN
1
(Q
2
, x) +(1 −y)F
eN
2
(Q
2
, x)
=
(y −1)
2
+1
i
f
i
(x)q
2
i
x ,
s = const . (3.74)
This equation (3.74) holds for all scattering processes, i.e., for any value of E,
E
,andθ. We use this fact by letting the parameter s = 2M
N
E,whichwasfixed
up to now, vary:
s → s
=
s
s
s . (3.75)
Simultaneously, we substitute
u →
s
s
u = u
, Q
2
→
s
s
Q
2
= Q
2
. (3.76)
x and y are not changed under the simultaneous transformations
y →
s
+u
s
=
s +u
s
, x →
Q
2
s
+u
=
Q
2
s +u
, (3.77)
or
y
= y , x
= x . (3.78)
Since the right-hand side of (3.74), computed in the parton model, depends
only on the variables x and y, and is therefore invariant under the scaling
transformations (3.75)–(3.77), it follows for the left-hand side that
xy
2
F
eN
1
(Q
2
, x) +(1 −y)F
eN
2
(Q
2
, x) = const for all Q
2
= Q
2
, (3.79)
which implies that the functions F
eN
1
(Q
2
, x) and F
eN
2
(Q
2
, x) do not depend
on Q
2
at all, i.e.
F
eN
1
(Q
2
, x) = F
eN
1
(x), F
eN
2
(Q
2
, x) = F
eN
2
(x). (3.80)
The structure functions in the parton picture thus no longer depend on Q
2
.
Since we have neglected here both the momenta coming from the binding of
the partons and the nucleon mass, (3.79) should hold for sufficiently large values
for Q
2
. This has indeed been experimentally observed as discussed above. It is
