Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


3. Scattering Reactions and the Internal Structure
of Baryons
3.1 Simple Quark Models Compared
In the first chapter we showed that the baryon spectrum by itself already suggests
that baryons are composed of quarks. However, the interaction between quarks
cannot be easily deduced from the energies of the states, since different models
yield nearly identical and well-fitting descriptions of the mass spectrum. Such
models include the flavor SU(6) model, the MIT bag model, the Skyrmion bag
model, and potential models with nonrelativistic quarks. Luckily lattice calcula-
tions are now good enough to demonstrate that the correct model, namely QCD,
gives equally good results.
The flavor SU(6) model postulates that the up, down, and strange quark
species are eigenvalues of an internal symmetry group, namely SU(3). To include
spin and thus the splitting between the spin-
1
2
and spin-
3
2
multiplets, this group
is extended to SU(6) ⊃ SU(2) ⊗ SU(3). This symmetry is then broken in such
a manner that the mass terms that appear depend only on operators that can be
diagonalized simultaneously. In this way we obtain mass formulas that describe
mass differences in a multiplet. The simplest expression is the Gürsey–Radicati
mass formula:
1
M = a +bY +c
T(T +1) −
1
4
Y
2
+dS(S +1) ; (3.1)
Y, T ,andS are the hypercharge, isospin, and spin of the baryon. Using the four
parameters a to d we can fit the lowest baryon resonances very well. With
a = 1065.5MeV, b =−193 MeV, c = 32.5MeV, and d = 67.5MeV,
(3.2)
for example, the numbers given in Table 3.1 are obtained. To describe the other
baryons as well an internal angular momentum must be introduced, i.e., we sup-
pose that quarks inside baryons can fill states with any angular momentum. As
the rotation group is O(3), we are thus led to the SU(6) ⊗O(3) symmetry group.
Indeed we can describe the full baryon spectrum starting from the SU(6) ⊗
O(3) mass formulas. Owing to the size of the symmetry group, many different
1
see, e. g., W. Greiner and B. Müller: Quantum Mechanics: Symmetries (Springer,
Berlin, Heidelberg, 1994).
78 3. Scattering Reactions and the Internal Structure of Baryons
Table 3.1. The Gursey–Radicati mass formula
Particles Mass from (3.1) Experimental data
N1/2
+
939 MeV 939 MeV
Λ1/2
+
1116 MeV 1116 MeV
Σ1/2
+
1181 MeV 1189 MeV
Ξ1/2
+
1325 MeV 1318 MeV
∆3/2
+
1239 MeV 1230–1234 MeV
Σ3/2
+
1384 MeV 1385 MeV
Ξ3/2
+
1528 MeV 1533 MeV
Ω3/2
+
1672 MeV 1672 MeV
contributions appear, making the procedure rather tedious.
2
Also the discov-
ery of every new quark, such as the charm, bottom and top quarks, demands an
extension of the flavor SU(6) model, leading to yet more complicated and un-
satisfactory models. The extremely large masses of the heavy quarks signal that
flavor symmetry is heavily broken, rendering such models much less attractive.
In the MIT bag model, presented in Sect. 3.3, quarks can occupy all states
satisfying the specific boundary conditions. Such states exist for any angular mo-
mentum, i.e., the single-particle spectrum of the quarks contains all states known
from atomic physics: s
1/2
, p
1/2
, p
3/2
, d
3/2
, d
5/2
, ... . In principle, many-particle
states with definite spin and parity could be constructed from this, thus deriv-
ing the corresponding masses from the bag boundary conditions. However, this
procedure gives disastrously bad results. To improve these, additional residual
interactions (like the one-gluon exchange) and other corrections can be taken
into account, but satisfactory baryon spectra are obtained only after introducing
a sufficiently large number of parameters.
3
Also the Skyrmion bag model, which is based on totally different assump-
tions, yields similar results. There the baryon number is regarded as a topological
quantum number. We shall not investigate this model further but shall il-
lustrate the basic idea with a simple example. As we remarked in Sect. 1.1,
spin and isospin are isomorphic. In particular, the regular representation of
isospin, e.g., pions, with its three isospin unit vectors |π
0
,
1
√
2
(|π
+
+|π
−
) and
1
√
2i
(|π
+
−|π
−
) is isomorphic to angular momentum. As angular momenta
can be represented by vectors in three-dimensional space, pions also can be
interpreted as vectors in three-dimensional isospin space. A very interesting con-
struction is now obtained by coupling the direction of this isospin vector to the
position vector, for example by demanding that the isospin vector t at position
x points in the direction t = x/|x| in isospin space. In this way we obtain a pion
2
For a discussion, see M. Jones, R.H. Dalitz, and R.R. Hougan: Nucl. Phys. B 129,45
(1977).
3
See, for example, T.A. De Grand and R.L. Jaffe: Ann. Phys. 100, 425 (1976) and
T.A. De Grand: Ann. Phys. 101, 496 (1976).

3.1 Simple Quark Models Compared 79
Table 3.2. A test of the potential model
Particles Potential model Experiment
N1/2
−
1490 MeV 1520–1555 MeV
N1/2
−
1655 MeV 1640–1680 MeV
N3/2
−
1535 MeV 1515–1530 MeV
N3/2
−
1745 MeV 1650–1750 MeV
Λ1/2
−
1490 MeV 1407 ±4MeV
Λ1/2
−
1650 MeV 1660–1680 MeV
Λ1/2
−
1800 MeV 1720–1850 MeV
Λ3/2
−
1490 MeV 1519.5±1MeV
Λ3/2
−
1690 MeV 1685–1695 MeV
Λ3/2
−
1880 MeV ?
field consisting purely of π
0
s along the z axis and of a mixture of π
0
, π
+
,andπ
−
at other positions (see Fig. 3.1). This construction is termed the hedgehog solu-
tion (because the isospin vectors point outwards like the spikes of a hedgehog).
To reverse this orientation of the pion field, one would have to change π(x) in
an infinite spatial domain (at |x|→∞), which would require infinite energy.
Thus a single hedgehog is stable, and the number of hedgehogs can be identi-
fied with the baryon number. More precisely, a topological quantum number is
defined that specifies how often π(|x|) covers all isospin values for |x|→∞.
The different states with topological quantum number 1 are then identified with
the different baryons.
Potential models simply solve the Schrödinger equation for nonrelativistic
quarks including a spin–spin and spin–tensor interaction. The basic Hamiltonian
is
H =
i
p
2
i
2m
i
+
1
2
K
i> j
V
2
ij
+
i> j
2α
s
3m
i
m
j
#
8π
3
s
i
· s
j
δ
3
(r) +
1
r
3
3(s
i
·r)( s
j
·r) − s
i
· s
j
&
+U(r
ij
). (3.3)
The coupling constants K , α
s
, the masses m
i
, and the (weak) residual interaction
are fitted to the baryon ground states,
4
and excited states are then predicted. As
Table 3.2 shows, the predictions obtained in this way coincide rather well with
experimental values.
5
4
See, for example, N. Isgur and G. Karl: Phys. Rev. D 19, 2653 (1979a).
5
See A.J.G. Hey and R.L. Kelly: Phys. Rep. 96, 72 (1983).
Fig. 3.1. The schematic
form of the hedgehog solu-
tion

80 3. Scattering Reactions and the Internal Structure of Baryons
In conclusion, completely different models describe the mass spectrum
equally well, which implies that nothing can be learned about the underlying
interaction from baryon masses alone. Also other parameters, such as magnetic
moments, do not give more information. However, there are experimental results
which are really sensitive. These are the so-called structure functions deduced
from scattering reactions. Their definition, measurement, and meaning will be
discussed in detail in this chapter. Structure functions are sensitive to the de-
tails of the interaction to such an extent that, contrary to the situation with the
mass formulas, no current model yields a really satisfactory description. Only
a complete solution of quantum chromodynamics could achieve this.
3.2 The Description of Scattering Reactions
To learn about the internal structure of nucleons, we must consider the scatter-
ing of particles as pointlike as possible, such as the scattering of high-energy
electrons, muons, or neutrinos off nucleons:
e
−
(E 1GeV) +N →e
−
... , (3.4)
ν
e
(E 1GeV) +N →e
−
... . (3.5)
Since highly energetic leptons have a very small wavelength, namely λ ≈ 1/E <
0.2 fm, and do not possess a resolvable internal structure, the cross sections of
these reactions depend solely on the internal structure of the nucleon. As electron
scattering takes place mainly by photon exchange, it senses the electromagnetic
charge distribution, whereas reaction (3.5) occurs through the weak interaction
and gives information about the corresponding distribution of “weak charge”. By
comparing the results of different scattering reactions, we thus obtain a nearly
complete description of the internal structure of the nucleon. The internal struc-
ture of baryon resonances and heavy mesons cannot, of course, be determined in
this way because of the small lifetime of these particles. Although some infor-
mation can be obtained from their decay properties, only the structure functions
of the proton, neutron, and pion are known.
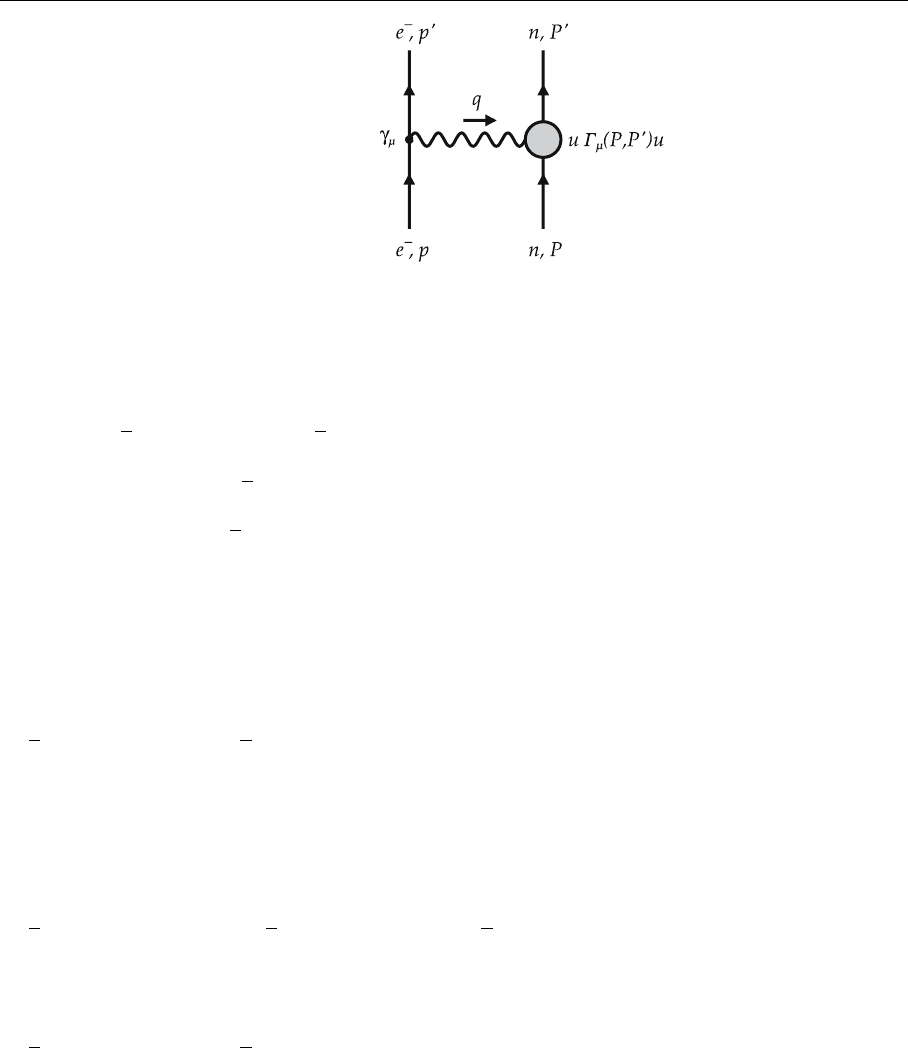
We shall now discuss the scattering of an electron off a nucleon. This is often
discussed in textbooks on quantum electrodynamics, leading to the Rosenbluth
formula.
6
We shall shortly repeat this discussion and introduce a new, more prac-
tical notation for the process of Fig. 3.2. Since QED is Lorentz-covariant, the
vertex function Γ
µ
(or, more precisely, the matrix element
¯
u(P
, S
)Γ
µ
u(P, S))
must be a Lorentz vector. The most general structure of Γ
µ
is thus
Γ
µ
= Aγ
µ
+BP
µ
+CP
µ
+iDP
ν
σ
µν
+iEP
ν
σ
µν
, (3.6)
6
see, e. g., W. Greiner and J. Reinhardt: Quantum Electrodynamics, 3rd ed. (Springer,
Berlin, Heidelberg, 2003).
3.2 The Description of Scattering Reactions 81
Fig. 3.2. Elastic electron-
nucleon scattering
where the quantities A, B, ..., E depend only on Lorentz-invariant quantities.
Since all these invariants can be expressed in terms of M
2
N
and q
2
, because
P · P = P
· P
= M
2
N
,
P · P
=−
1
2
(P − P
)
2
+M
2
N
=−
1
2
q
2
+M
2
N
,
P ·q = P · P
− P
2
=−
1
2
q
2
,
P
·q = P
2
− P
· P =
1
2
q
2
. (3.7)
Therefore, A = A(q
2
), B = B(q
2
), etc. hold. From the demand for gauge invari-
ance, it follows, on the other hand, that
q
µ
¯
u(P
)Γ
µ
u(P) = 0 . (3.8)
Substituting from (3.6) yields D =−E and C = B and thus
u(P
)Γ
µ
(P
, P) u(P) = u(P
)
A(q
2
)γ
µ
+B(q
2
)(P
+ P)
µ
+iD(q
2
)(P
− P)
ν
σ
µν
u(P). (3.9)
On physical grounds we demand that the transition current must be Hermitian.
For (3.9) to be invariant under the transformation (...)
+
|P
µ
→ P
µ
, A, B,and
D must be real (see Exercise 3.3). Using the Gordon decomposition,
6
u(P
)γ
µ
u(P) =
P + P
µ
u(P
) u(P) +i
P
− P
ν
u(P
)σ
µν
u(P)
the second term on the right-hand side can be expressed by the first and the third
terms, and we get
u(P
)Γ
µ
(P
, P) u(P) = u(P
)
A(q
2
)γ
µ
+iB(q
2
)q
ν
σ
µν
u(P). (3.10)
Note that the functions A(q
2
) and B(q
2
) occurring here are not identical with, but
related to the functions A(q
2
), B(q
2
),andD(q
2
) in equation (3.9). The absolute
82 3. Scattering Reactions and the Internal Structure of Baryons
square of expression (3.10) enters in the cross section. Hence one is led to the
expression
W
µν
=
1
2
spin
u(P
)Γ
µ
u(P)
∗
u(P
)Γ
ν
u(P)
(3.11)
=
1
2
tr
(Aγ
µ
−iBq
λ
σ
µλ
)(P/
+M
N
)(Aγ
ν
+iBq
σ
ν
)(P/ +M
N
)
.
where we have utilized the relation γ
0
ˆ
Γ
†
µ
γ
0
=
ˆ
Γ
µ
, which can be directly verified
in the standard representation of the γ
µ
.Notethatwehavehaveusedherethe
normalization convention for the spinors u and v expressed in (2.50). Therefore
the projection operator is
S
u(P, S)u(P, S) = P/ +M
N
. Remember that in the
spinor normalization used standardly in QED, the right-hand side would be (P/ +
M
N
)/2M
N
.
After some lengthy calculation we find that
W
µν
=2(A +2M
N
B)
2
P
µ
P
ν
+ P
µ
P
ν
−
P · P
−M
2
N
g
µν
+
'
−4(A +2M
N
B)M
N
B +2M
2
N
B
2
P · P
M
2
N
+1
(
×(P
µ
+ P
µ
)(P
ν
+ P
ν
). (3.12)
Replacing P
µ
by q
µ
+ P
µ
yields
W
µν
=2(A +2M
N
B)
2
P
µ
q
ν
+ P
ν
q
µ
+2P
µ
P
ν
+
q
2
2
g
µν
+
'
−4(A +2M
N
B)M
N
B +2M
2
N
B
2
−
q
2
2M
2
N
+2
(
×(q
µ
+2P
µ
)(q
ν
+2P
ν
), (3.13)
and using
P
µ
q
ν
+ P
ν
q
µ
+2P
µ
P
ν
=
1
2
(q
µ
+2P
µ
)(q
ν
+2P
ν
) −
1
2
q
µ
q
ν
(3.14)
we get for (3.13)
W
µν
=−(A +2M
N
B)
2
q
2
q
µ
q
ν
q
2
−g
µν
+
A
2
−B
2
q
2
4
P
µ
−q
µ
P ·q
q
2
P
ν
−q
ν
P ·q
q
2
. (3.15)
In the last step, we have used the fact that, owing to (3.7), P ·q/q
2
=
1
2
.Wenow
introduce two new functions W
1
, W
2
and the variable Q
2
=−q
2
and write the
3.2 The Description of Scattering Reactions 83
elastic scattering tensor as
W
elastic
µν
=
−g
µν
+
q
µ
q
ν
q
2
W
1
(Q
2
)
+
P
µ
−q
µ
P ·q
q
2
P
ν
−q
ν
P ·q
q
2
W
2
(Q
2
)
M
2
N
. (3.16)
This structure is immediately evident if one considers that, owing to gauge
invariance,
q
µ
W
elastic
µν
=q
ν
W
elastic
µν
=0 . (3.17)
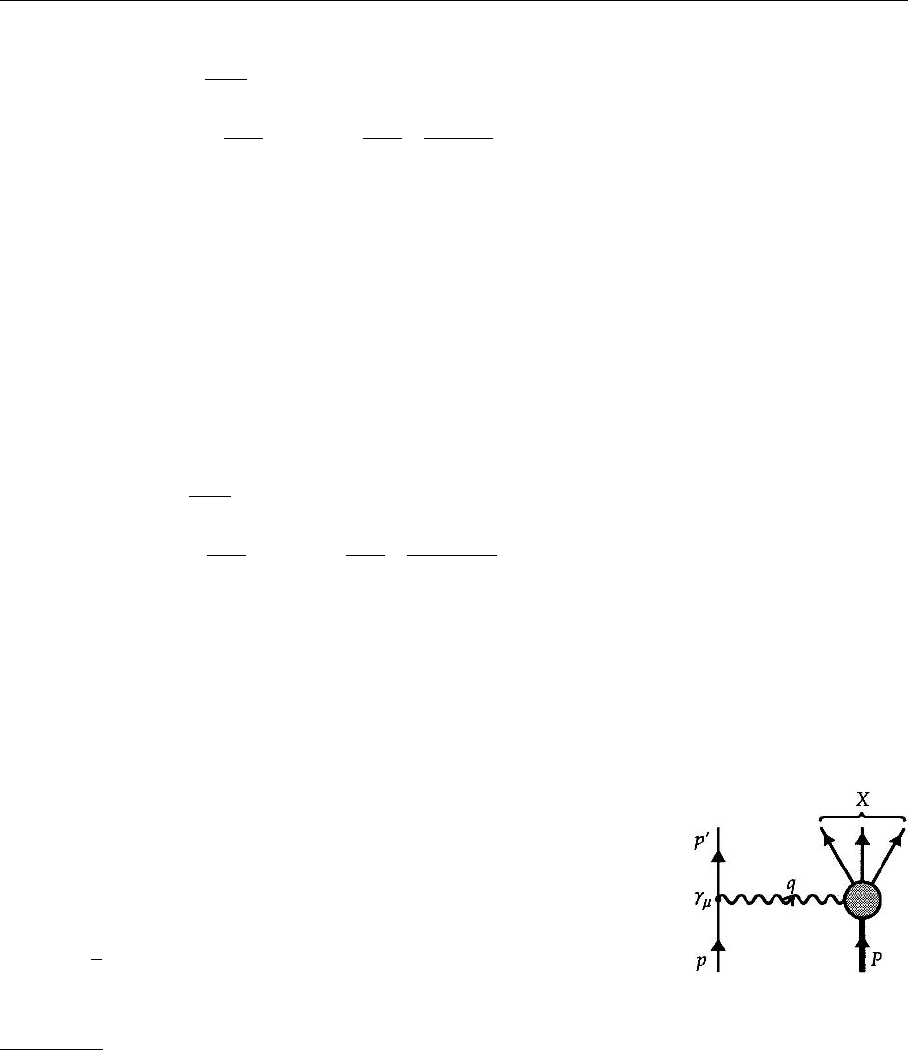
If we consider instead of elastic scattering special inelastic processes like
e +N →e +N +π, more momentum vectors can be combined and the general
structure of W
µν
becomes more complicated. However, a simple expression can
again be obtained if one sums over all possible processes or, more precisely, over
all possible final hadron states, since this sum can again only depend on P and q.
The only change is that the Lorentz invariants q
2
and q · P are now independent.
One thus obtains the following general form for the inclusive inelastic scattering
tensor:
W
incl.
µν
=
−g
µν
+
q
µ
q
ν
q
2
W
1
(Q
2
,ν)
+
P
µ
−q
µ
P ·q
q
2
P
ν
−q
ν
P ·q
q
2
W
2
(Q
2
,ν)
M
2
N
(3.18)
with the inelasticity variable
7
ν = P ·q . (3.19)
In the rest frame of the proton ν = M
N
(E
−E), i.e. it equals the energy loss of
the electron (see (3.28) below). At low energies, the energy loss of the electron
will end up in a recoil energy of the nucleon. At high energies, however, most of
the energy will go into production of other particles, mostly pions. It is therefore
justified to call ν inelasticity variable.
The two functions W
1
(Q
2
,ν) and W
2
(Q
2
,ν) are called structure functions
for inclusive electron–nucleon scattering. They are most important because they
precisely exhibit the impact of the structure of the nucleon on the inclusive cross
section. All the rest in (3.18) is relativistic kinematics! To obtain the differen-
tial cross section, we must multiply W
µν
with the corresponding tensor for the
electrons
L
µν
=
1
2
tr
$
( p/ +m)γ
µ
( p/
+m)γ
ν
%
=2
p
µ
p
ν
+ p
ν
p
µ
−g
µν
p · p
+g
µν
m
2
. (3.20)
7
In the literature one may also find the following definition for ν: ν = P ·q/M
N
.It
differs from our definition by the factor 1/M
N
. We shall use the definition (3.19)
throughout this book. It is the one standardly used in connection with the operator
product expansion and the DGLAP equations (see Chap. 5).
Fig. 3.3. Inclusive inelastic
electron–nucleon scattering

84 3. Scattering Reactions and the Internal Structure of Baryons
Equation (3.20) can be obtained by setting A = 1, B = 0 in (3.12). (The factor
1
2
comes from averaging over the spin directions of the incoming electrons.) The
other factors appearing are the coupling constant and the photon propagator
e
2
q
2
2
=
e
4
Q
4
. (3.21)
Finally, this must be multiplied with normalization and phase-space factors
(cf. Example 3.1). The final expression for unpolarized electron–nucleon scat-
tering in the laboratory system is
d
2
σ
dE
dΩ
=
E
α
2
EQ
4
L
µν
W
µν
. (3.22)
Here E and E
are defined by
p
µ
=(E, p),
p
µ
=(E
, p
), (3.23)
and the electron mass has been neglected (the extremely relativistic approxima-
tion).
Substituting (3.18) and (3.20) into (3.22), this yields
d
2
σ
dE
dΩ
=
E
α
2
EQ
4
2(2p
µ
p
ν
−g
µν
p · p
) (3.24)
×
'
−g
µν
+
q
µ
q
ν
q
2
W
1
+
P
µ
−q
µ
P ·q
q
2
P
ν
−q
ν
P ·q
q
2
W
2
M
2
N
(
.
Because q
µ
W
µν
= 0, we were able to replace p
µ
= p
µ
−q
µ
by p
µ
, and we have
again neglected the electron mass in comparison with p
µ
and p
µ
.Weshallsetit
to zero in the following. Taking into account that
−Q
2
=q
2
≈−2 p · p
(3.25)
and
2 p ·q = 2 p ·( p − p
) = 2m
2
−2 p · p
≈−Q
2
, (3.26)
we obtain
d
2
σ
dE
dΩ
=
E
E
α
2
Q
4
2
'
2
( p ·q)
2
q
2
+3 p · p
W
1
+2
P · p −
q · p
q
2
q · P
2
W
2
M
2
N
−
P
µ
−q
µ
q · P
q
2
2
p · p
W
2
M
2
N
(
=
E
E
2α
2
Q
4
'
Q
2
W
1
+2
P · p −
1
2
P ·q
2
W
2
M
2
N
−
Q
2
2
M
2
N
−
(P ·q)
2
q
2
W
2
M
2
N
(
. (3.27)
3.2 The Description of Scattering Reactions 85
Let us look at the scattering in the laboratory system, in which the nucleon is at
rest before the collision, i.e.,
P
µ
= (M
N
, 0), ν = P ·q = P ·( p − p
) = M
N
(E −E
). (3.28)
In addition we introduce the scattering angle θ of the electron in the laboratory
system; thus
p · p
=|p||p
|cos(θ) = EE
cos(θ) (3.29)
and
Q
2
=2 p · p
= 2(EE
− p · p
) = 4EE
sin
2
θ
2
. (3.30)
Finally we use definition (3.19):
d
2
σ
dE
dΩ
=
E
E
α
2
Q
4
2
)
4EE
sin
2
θ
2
W
1
+2M
2
N
E −
ν
2M
N
2
W
2
M
2
N
−
'
2EE
sin
2
θ
2
+
ν
2
2M
2
N
(
W
2
*
=
E
E
α
2
Q
4
2
#
4EE
sin
2
θ
2
W
1
+
2E
2
−2E(E −E
) −2EE
sin
2
θ
2
W
2
&
. (3.31)
Because ν = (P ·q) = (P · p − P · p
) = M
N
(E −E
), the last term simplifies to
give
2M
2
N
EE
1 −sin
2
θ
2
W
2
M
2
N
= 2EE
cos
2
θ
2
W
2
, (3.31a)
and we obtain
d
2
σ
dE
dΩ
eN
=4E
2
α
2
Q
2sin
2
θ
2
W
1
Q
2
,ν
+cos
2
θ
2
W
2
Q
2
,ν
.
(3.32)
This is the final expression for the inclusive unpolarized electron–nucleon
scattering cross section. As mentioned before, the functions W
1
Q
2
,ν
and
W
2
Q
2
,ν
are called the structure functions of inclusive electron–nucleon scat-
tering. To avoid confusion, we write them in what follows as W
eN
1
Q
2
,ν
and
W
eN
2
Q
2
,ν
. Experimentally one measures for a definite electron beam energy
the direction and energy of the scattered electrons and sums the total reac-
tion cross section for each (θ, E
) bin. From this one obtains W
eN
1
Q
2
,ν
and
W
eN
2
Q
2
,ν
.

86 3. Scattering Reactions and the Internal Structure of Baryons
What now is the advantage of (3.32)? So far we have only managed to elimi-
nate one of the three parameters E, E
,andθ. While d
2
σ/dE
dΩ can in general
be any function of E, E
,andθ, we have to express it by arbitrary functions of Q
2
and ν. The importance in (3.32) lies mainly in the fact that the structure functions
W
1
Q
2
,ν
and W
2
Q
2
,ν
can be calculated from the microscopic properties of
the quark model and that then the variables x = Q
2
/2ν (see (3.39) below) and
Q
2
are the relevant ones. In the leading order of α
s
the structure functions turn
out to be Q
2
independent. Only a very tiny Q
2
dependence is observed. This re-
sidual Q
2
dependence can be used, however, as a most sensitive test for the quark
interaction, i.e., for QCD.
W
eN
µν
can be expressed by
W
eN
µν
(P, q) =
1
2π
d
4
x e
iq·x
1
2
pol.
N(P)|
ˆ
J
µ
(x)
ˆ
J
ν
(0)|N(P) , (3.33)
where |N(P) designates the state vector of a nucleon with momentum P and
ˆ
J
the electromagnetic current operator. The derivation of this relation will be
given in Example 3.2.
In the laboratory frame P
µ
=(M, 0). Also, we can orient the coordinate
system such that q points in the z direction. Then from (3.18) it holds that
W
eN
00
=
q
0
q
0
q
2
−1
W
eN
1
Q
2
,ν
+
1 +
ν
Q
2
q
0
2
W
eN
2
Q
2
,ν
(3.34)
and
W
eN
11
= W
eN
1
Q
2
,ν
(3.34a)
with
q
0
= E −E
=ν/M
N
. (3.35)
For W
eN
1
Q
2
,ν
one has according to (3.33):
W
eN
1
Q
2
,ν
=
1
2π
d
4
x e
iq·x
1
2
pol.
N(P)|
ˆ
J
1
(x)
ˆ
J
1
(0)|N(P) . (3.36)
The right-hand side can (at least in principle) be computed for any quark
model, and its correctness can thus be tested by comparing the result with the
experimental values for W
eN
1
and W
eN
2
.
We shall illustrate the calculation and the meaning of the nucleon structure
functions for a very simple, but inadequate, model in Exercise 3.9. This model
is indeed so simple that we do not need to use (3.36) but can choose a simpler
way to calculate W
eN
1
Q
2
,ν
.
Before we discuss the experimentally determined properties of structure
functions and their meaning, we give the analogous result for neutrino–nucleon
