Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

46 2. Review of Relativistic Field Theory

Exercise 2.6

where we have inserted (20). Finally we introduce the Mandelstam variable s

(see Exercise 2.3) and take p

= m

and p

= m

into account. Equation (27)

then assumes the form

dσ

16π

|F|



s −(m

)



s −(m

−m

)



. (28)

As already mentioned these expressions are valid for any scattering reaction with

two unpolarized particles in both initial and ﬁnal states. Now we want to express

|F|

in the case of π

scattering by invariant Mandelstam variables.From

the deﬁnitions

s = ( p

+ p

)

=( p

+ p

)

u = ( p

− p

)

=( p

− p

)

(29)

we derive the relations

2 p

· p

= 2 p

· p

= s −m

−m

2 p

· p

= m

−u . (30)

With the help of these relations the invariant scattering amplitude (2) assumes

the form

|F|



4πα



(s −u)

, (31)

where we have transformed the ﬁne-structure constant

α =

4π



137

(32)

to so-called Heaviside–Lorentz units. In these units Gauss’s law reads ∇ ·E = .

It is particularly simple to transform (31) into the cm system, since we have,

according to (29) and (5),

s = (E

, 0)

= E

cms

u = (E

−E

, p + p



)

= (E

−E

)

−( p + p



)

= E

−2E

−(E

−m

) −(E

−m

) −2 p · p



= m

−2 p

cos(θ

cms

) −2E

t =−2p

(

1 −cos(θ

cms

)

. (33)

The variable t has already been given in (23).

2.2 Scalar Quantum Electrodynamics 47

2.2.5 Spin-1 Particles and Their Polarization

In the preceding sections on the basic elements of scalar QED we discussed the

scattering of charged spin-0 mesons. Their mutual interaction is mediated by the

exchange of virtual photons (massless spin-1 vector bosons). The kind of vir-

tual quanta exchanged is of course speciﬁc for each interaction. For example in

pion Compton scattering, virtual pions are exchanged (see Example 2.8), and the

weak interaction in lepton scattering is mediated by vector bosons (Z

, W

One difference between such particles is the number of internal degrees of

freedom, which depends on their spin (or polarization).

Massive Spin-1 Particles. Massive spin-1 bosons are described in the frame-

work of the Proca theory. From the Lagrangian density of the classical four-

vector ﬁeld φ

(x)

L =−

µν

, (2.121a)

µν

= ∂

−∂

, (2.121b)

the wave equation follows:

∂

αµ

= 0 . (2.122)

Taking the four-divergence of this equation, we ﬁnd that

∂

=0 . (2.123)

As it is assumed here that M

= 0, the divergence of φ

vanishes, and (2.122) is

reduced to the Proca equation



 + M



= 0 ,∂

= 0 . (2.124)

We ﬁrst consider the polarization vectors of these massive vector bosons. In the

rest system of such particles there are three possible positions for spin 1, i.e.,

three spin vectors, which can generally be chosen as

(1)

(

1, 0, 0

)

(2)

(

0, 1, 0

)

(3)

(

0, 0, 1

)

. (2.125a)

These obviously satisfy the orthogonality relations

(i)

·ε

( j)

=δ

. (2.125b)

It is more useful to use the spherical representation ε(λ) with

ε(λ =1) =−

√

(

1, i, 0

)

ε(λ =0) =

(

0, 0, 1

)

ε(λ =−1) =

√

(

1, −i, 0

)

, (2.126a)

48 2. Review of Relativistic Field Theory

and

∗

(λ) ·ε(λ



) = δ

λλ



(2.126b)

instead of the Cartesian representation (2.125a).

In the massless case, i.e., for photons, this change of basis vectors corres-

ponds to the transition from linearly to circularly polarized light. As is known

from nonrelativistic quantum mechanics, λ =±1, 0 is the projection of the

particle’s spin on, for example, the z axis.

We shall now formulate (2.126) in a manifestly covariant way. For a spin-1

particle in motion, four-vectors ε

(λ) must be found that transform into (2.126)

in the rest frame. Setting in the rest frame

(λ) = 0 , for λ = 0, ±1 (2.127)

and thus deﬁning (in the rest frame)

(λ) =



(λ), ε(λ)



, (2.128)

the polarization vector in any other inertial system can be found by the Lorentz

transformation. Since the four-momentum in the rest frame is given by

(

M, 0

)

, (2.129)

it follows that

p ·ε(λ) = 0 . (2.130)

Equation (2.130) is basically a direct consequence of the condition ∂

0, since it reduces the number of relevant degrees of freedom to 3. Since

a general free solution of the wave equation (2.124) can always be written as

a superposition of linearly independent solutions in the form

(x) =



λ=0,±1

( p;λ) e

−i p·x

, p

= M

(2.130) becomes evident. The normalization of polarization vectors is given by

∗µ

( p;λ)ε

( p;λ



) = ε

∗

( p;λ)ε

( p;λ



) =−δ

λλ



. (2.131)

Let us consider, for example, a system in which the particle is moving along the

z axis with momentum p. Hence its four-momentum is

=(E, 0, 0, p), |p|≡p , (2.132)

and we recognize immediately from (2.130) that the tranverse polarization

vectors in this system are the same as those in the rest system,

( p;λ =±1), (2.133)

2.2 Scalar Quantum Electrodynamics 49

but that the longitudinal polarization vector must be given by

( p;λ = 0) =

( p, 0, 0, E), (2.134)

in order to satisfy (2.130) and the normalization (2.131). It turns out that the

p and E dependence of the longitudinal polarization vector have very interest-

ing consequences for massive spin-1 particles such as the Z and W

bosons

mediating the weak interaction. The polarization vectors ε

( p;λ) satisfy the

completeness relation



∗

( p;λ)ε

( p;λ) =−g

µν

, (2.135)

which we shall prove in Exercise 2.7. The factor on the right-hand side projects

out the physical states and appears, as we shall see, in the propagator of virtual

spin-1 particles.

EXERCISE

2.7 Polarization States of a Massive Spin-1 Particle

Problem. The polarization vectors of a massive spin-1 particle with four-

momentum p

and helicity λ are denoted by ε

( p;λ). It holds that

∗

( p;λ)ε

( p;λ



) = ε

∗

( p;λ)ε

( p;λ



) =−δ

λλ



. (1)

The minus sign occurs because these vectors are spacelike. Owing to Lorentz

covariance, the sum over the polarization states



∗

( p;λ)ε

( p;λ) ≡ η

µν

( p) (2)

has to be of the form

µν

( p) = Ag

µν

+Bp

. (3)

Find arguments for this fact and determine the constants A and B.Makeuseof

scalar multiplications by p

, p

,andg

µν

. Note that g

µν

=4.

Solution. The condition ∂

=0 for the wave function of a spin-1 particle

leads to p

( p;λ) = 0. Here p

and ε

( p;λ) are a system of four linearly

independent, orthogonal vectors; i.e., any four-vector a

can be represented as

a linear combination



( p;λ) . (4)

50 2. Review of Relativistic Field Theory

Exercise 2.7

Now we evaluate

µν

( p) =





∗

( p;λ) +





∗

( p;λ)ε

( p;λ



)



( p;λ)





·0+





(−δ

λλ





( p;λ)

=−



( p;λ) . (5)

( p;λ) and shows that −η

µν

( p) eliminates the part of a given four-vector that

is proportional to p

. Therefore η

µν

( p) can only depend on p

, i.e., a

⊥

( p) =

−a

µν

( p). Since the ε

( p;λ) are four-vectors, the polarization sum η

µν

trans-

forms like a second-rank tensor. Any symmetric tensor of second rank that is

built by a four-vector p

is of the general form

µν

( p) = A( p

µν

+B(p

) p

. (6)

There are no other possibilities, because the only Lorentz-covariant quantities

available are g

µν

, p

,andp

.Herewehavep

= M

=const., and therefore A

and B must be constants. Multiplying the polarization sum by p

yields

µν



p ·ε

∗

( p;λ)ε

( p;λ) = 0

→ p

(Ag

µν

+Bp

) = (A + Bp

) p

= 0

→ B =−

. (7)

Hence the polarization sum assumes the form A(g

µν

− p

). A contraction

with g

µν

leads to

µν

( p) = η

( p) =



∗

( p;λ)ε

( p;λ)



(−δ

λλ

) =−3(8)

→η

( p) = Ag

+Bp

= A



−



= A(4 −1) = 3A

→ A =−1 . (9)

The ﬁnal result is then



∗

( p;λ)ε

( p;λ) =−



µν

−



. (10)

2.2 Scalar Quantum Electrodynamics 51

Massless Spin-1 Particles: Photons. Photons do not possess a rest system as

massive vector bosons do, since from p

=0 ↔|E| > 0 we immediately get

p =0 in any inertial frame. It is therefore impossible to proceed as for massive

spin-1 particles, formulating the polarization vectors in the rest frame and then

obtaining them in any frame by a Lorentz transformation, which was the method

just discussed. To ﬁnd the number of relevant internal degrees of freedom of the

photon ﬁeld we will use gauge invariance, which holds for massless, but not for

massive, vector bosons. It will turn out that real photons have only two transverse

polarization degrees of freedom.

We ﬁrst summarize. For a free photon ﬁeld, the wave equation and the

Lorentz condition are

A

=0 (2.136a)

∂

=0 (2.136b)

This auxiliary condition can be always satisﬁed in a special gauge – the Lorentz

gauge – and only in this gauge does the wave equation (2.136) have this simple

form. For p

= 0 (real photons) its solutions are plane waves

= Nε

−i p·x

, (2.137)

where N is a normalization factor and ε

the polarization vector of the photon.

The Lorentz condition (2.136b) leads immediately to the condition

p ·ε = 0 (2.138)

for the polarization vector. Equations (2.136) and (2.138) are analogous to

(2.124) and (2.130), derived for massive vector bosons. There ∂

followed di-

rectly from the ﬁeld equations (2.122) and p ·ε = 0wasﬁrstderivedintherest

frame and then recognized to be covariant in general. Now (2.136) and (2.138)

follow from an arbitrary choice of gauge for the photon ﬁeld. The Lorentz con-

dition (2.136) reduces the number of internal degrees of freedom to three. But as

we shall see in the following, the gauge condition reduces this number to two.

In the Lorentz gauge, one can still perform the symmetry transformation

→ A

−∂

Λ = A

µ

, (2.139)

provided Λ satisﬁes the Klein–Gordon equation for the massless scalar ﬁeld,

Λ = 0 . (2.140)

Such re-gauging obviously does not change the Lorentz condition (2.136b). An

example of a function Λ obeying the Klein-Gordon equation is given by Λ =

α e

−i p·x

. For the plane waves (2.137), this re-gauging amounts to changing the

polarization vector ε

by a multiple of p

−∂

Λ = Nε

−i p·x

−α∂

−i p·x

= N



+β p



−i p·x

, (2.141)

52 2. Review of Relativistic Field Theory

that is,

→ε



= ε

+β p

. (2.142)

Moreover, the condition



· p = 0 (2.143)

still holds since ∂

µ

=0 holds as well. The freedom expressed by (2.142) has

profound consequences. To illustrate this, we consider a photon with the four-

momentum



, p



(2.144)

and the polarization vector



, ε



, (2.145)

which satisfy the Lorentz condition ε · p = 0. Gauge invariance now allows us to

add, according to (2.142), any multiple of p

to ε

, still obtaining admittable po-

larization vectors. We can therefore always choose the gauge such that the time

component of ε

vanishes in (2.145) and the four-dimensional equation (2.143)

is reduced to the three-dimensional equation

ε· p = 0 . (2.146)

This means that there are only two linearly independent polarization vectors for

photons (massless bosons). For a plane photon wave propagating in the z direc-

tion, we can choose ε

(1)

and ε

(2)

from (2.125a) for linearly polarized photons and

ε(λ =+1) and ε(λ =−1) for circularly polarized photons.

This is the result – known from classical electrodynamics – that the electric

and magnetic ﬁeld strengths

µν

= ∂

−∂

are purely transverse. Although photons are described by a vector ﬁeld A

and

thus must have spin 1, there are only two independent spin projections and not

three, as one might naively expect.

As we have seen, this result is rooted in the

photons having no mass. If the wave equation (2.136) had a mass term, as in the

Proca equation (2.124), the theory would no longer be gauge invariant and gauge

freedom would be lost.

We thus describe incoming photons with four-momentum p and polarization

state λ by the wave function

= N ε

(λ)e

−i p·x

,λ=±1 , (2.147)

Any vector ﬁeld carries spin 1 – see W. Greiner and B. Müller: Quantum Mechanics:

Symmetries (Springer, Berlin, Heidelberg, 1994).

2.2 Scalar Quantum Electrodynamics 53

and outgoing photons by

= Nε

∗µ

(λ)e

i p·x

,λ=±1 . (2.148)

As in (2.131) for massive spin-1 particles, the orthogonality

∗

(λ) ·ε(λ



) =−δ

λλ



(2.149)

holds. Normalizing in the same way as with the pion wave function, we obtain

N =

√

(2.150)

as the normalization factor.

In a certain sense we can associate the gauge system where (2.146) holds, i.e.,

where photons are tranverse, to the rest system (2.126), (2.127) for particles with

a mass. In this rest system ε(λ) · p = 0 also holds, since the momentum p does

vanish there.

2.2.6 The Propagator for Virtual Photons

In view of the different fermion–boson scattering processes that will be derived

in the next section, we now proceed to derive the pion propagator. This deriva-

tion is completely analogous to that for the photon propagator. The equation

corresponding to (2.95) is



 +m



φ(x) ≡−J(x). (2.151)

The Green function for this inhomogeneous Klein–Gordon equation is



 +m



G(x −x



) =−iδ

(x −x



). (2.152)

By Fourier transformation, we obtain

G( p

) =

−m

+iε

(2.153)

where p

= m

has been assumed for virtual pions. We refer to standard QED

textbooks for the detailed proof

that the propagator is given by (2.153) and

that the Feynman interpretation of waves with positive and negative energy

corresponds to the +iε prescription for treating the poles in (2.153).

see, e. g., W. Greiner and J. Reinhardt: Quantum Electrodynamics, 3rd ed. (Springer,

Berlin, Heidelberg, 2003).

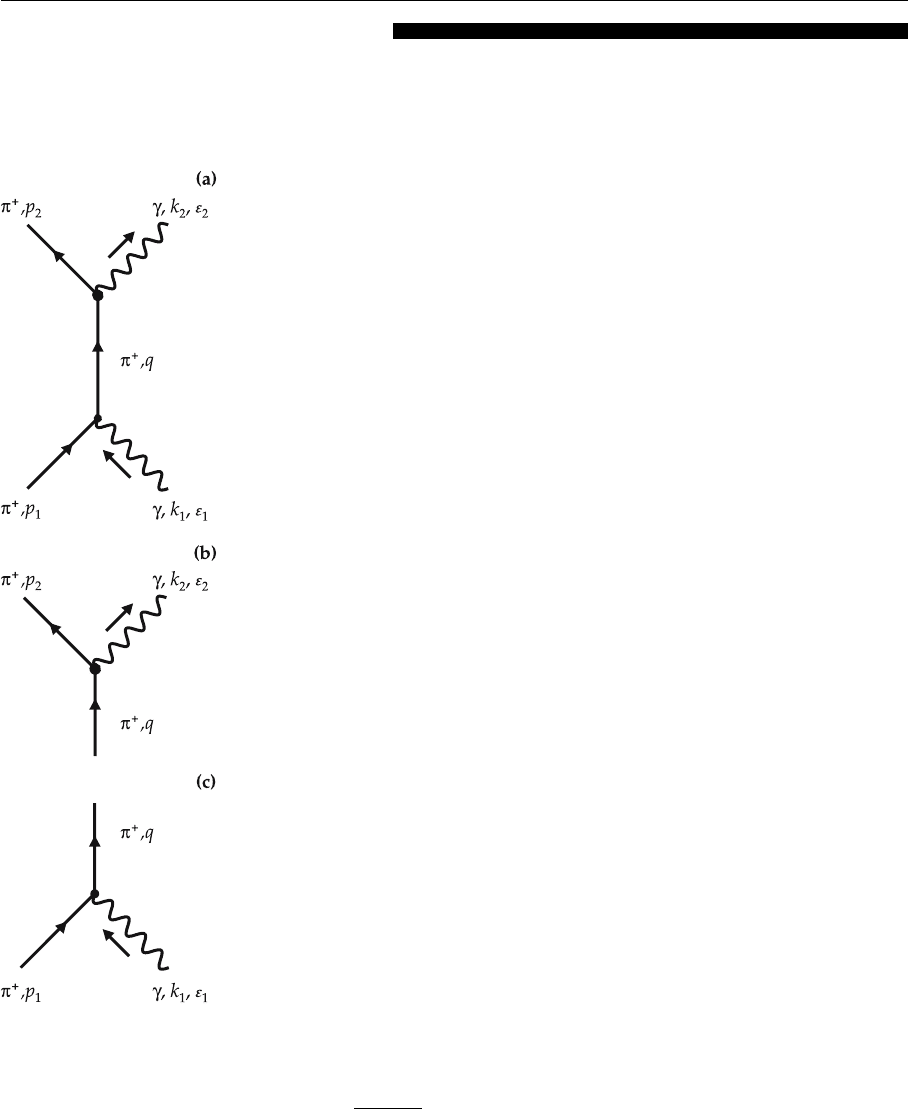
54 2. Review of Relativistic Field Theory

Fig. 2.15a–c. The direct

graph of π

γ Compton scat-

tering (a). The upper and

lower vertices are shown

separately in graphs (b)and

lower (c), respectively

EXAMPLE

2.8 Compton Scattering by Pions

Elastic photon scattering by a charged particle is called Compton scattering. In

the case of a pion this process is written as

γ +π

→γ +π

First we consider the direct graph (symmetrization is necessary!), which is de-

picted in Fig. 2.15a. The lower vertex, which is separately shown in Fig. 2.15c,

corresponds to the absorption of a photon with four-momentum k

and polariza-

tion ε

and to the transition of the pion state from p

to q. The corresponding

scattering amplitude is proportional to (cf. (2.89))

∼ie

x φ

∗

(π

, q)(∂

+ A

∂

)φ

(π

, p

). (1)

Here, φ

is the intermediate pion wave function. Inserting the plane waves

≈ e

−i p

·x

∗

≈ e

iq·x

≈ ε

−ik

·x

(2)

into (1) leads to a vertex amplitude proportional to

≈e( p

+q)

, (3)

where

q = p

(4)

denotes the four-momentum of the virtual photon. Energy-momentum conserva-

tion is ensured by the delta function

(q − p

−k

). (5)

An analogous procedure for the upper vertex in Fig. 2.15a (see Fig. 2.15b) leads

to the vertex amplitude

≈e(q + p

)

∗

(6)

with four-momentum conservation,

q = p

,δ

( p

−q). (7)

Putting graphs 2.14b and 2.14c together we obtain the complete direct graph

2.14a. Formally this connection is achieved by inserting the virtual pion prop-

agator

G(q

) =

−m

(8)

2.2 Scalar Quantum Electrodynamics 55

between the scattering amplitudes (3) and (6). The invariant scattering amplitude

for the direct graph of Compton scattering by a pion is then

(d)

γπ

= e

·(p

+q)

−m

∗

·(q + p

), (9)

where energy conservation is ensured by δ

( p

− p

−k

).Takinginto

account the Lorentz-gauge condition

·k

= 0 ,ε

·k

= 0 (10)

and introducing the Mandelstam variable

s = q

= ( p

)

= ( p

)

, (11)

we can easily transform (9) into

(d)

πγ

(ε

· p

)(ε

∗

· p

)

s −m

. (12)

Now we have to symmetrize with respect to the two photons (or the two pions).

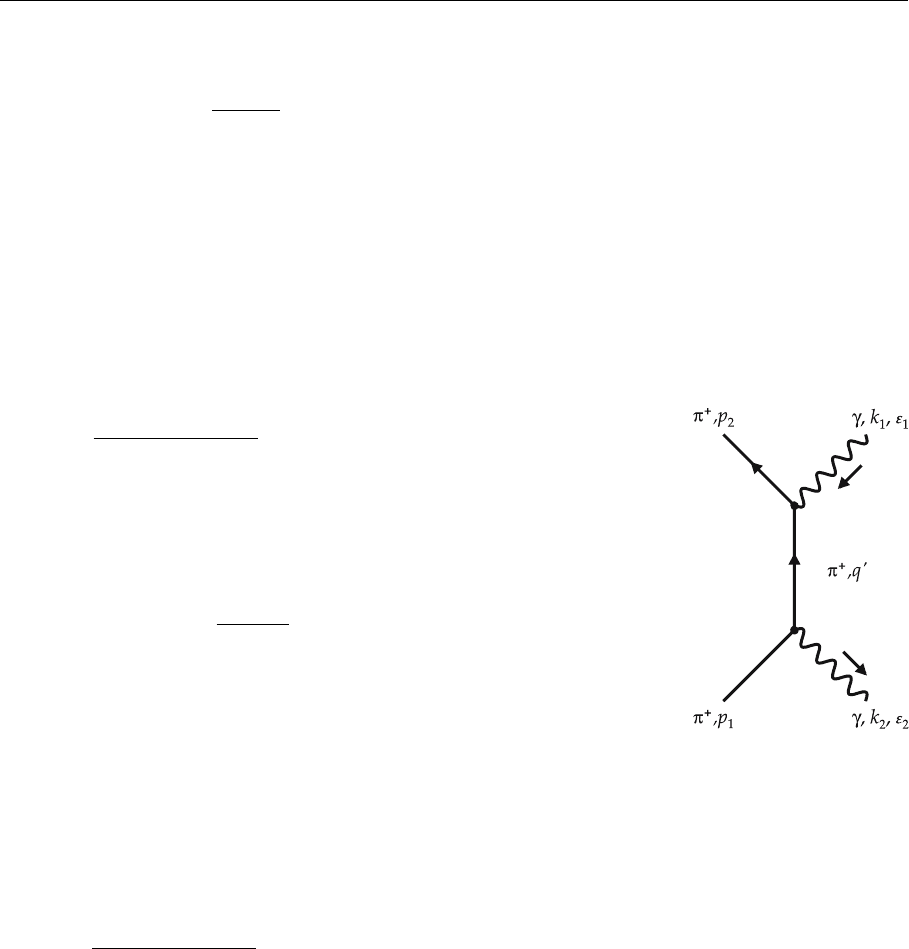
The resulting exchange graph for Compton scattering is shown in Fig. 2.16. First

the outgoing photon k

, ε

is emitted and later the incoming photon k

, ε

absorbed. In analogy to (9) the scattering amplitude for this process is

(e)

γπ

·(q



+ p

)

2

−m

∗

·(q



+ p

), (13)

with



= p

−k

= p

−k

. (14)

If we employ the Mandelstam variable

u = ( p

−k

)

=( p

−k

)

2

, (15)

which represents the squared mass of the virtual pion in the exchange graph, and

take (10) into account, the amplitude (13) assumes the form

(e)

γπ

(ε

· p

)(ε

∗

· p

)

u −m

. (16)

This exchange amplitude is sometimes called the u-channel contrib ution (am-

plitude).

Now the question arises whether there are contributions to Compton scatter-

ing that are of order e

caused by the squared interaction term

−e

. (17)

Example 2.8

Fig. 2.16. The exchange

graph for π

γ Compton

scattering