Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

470 7. Nonperturbative QCD
The integral measure is invariant under the unitary transformation:
I =
[d
˜
φ][d
˜
φ
∗
]e
−
˜
φ
∗
M
D
˜
φ
=
[d
˜
φ
re
][d
˜
φ
im
]e
−(
˜
φ
re
M
D
˜
φ
re
+
˜
φ
im
M
D
˜
φ
im
)
=
[d
˜
φ
re
]e
−
˜
φ
re
M
D
˜
φ
re
2
. (7.140)
In the last line we switched from the variables φ, φ
∗
to the real and the imagi-
nary φ
re
, φ
im
. Assuming, for simplicity, that the system is discretized, one can
integrate over each variable φ
i
= φ(x
i
) separately:
I = N
⎛
⎝
1
<
i
M
D
ii
⎞
⎠
2
=
N
det M
, (7.141)
where we absorbed all constants coming from the definition of the measure and
the integration in a factor N.
Considering this result and (7.137), we can write the partition function as
Z = N
[dφ][dφ
∗
][dU]e
−S
E
({U})−φ
∗
(M
F
({U}))
−1
φ
. (7.142)
One has to perform a path integral over the link variables and the auxiliary com-
plex field which replaces the fermion part (φ is therefore often called the “pseudo
fermion”). There still remains the tough numerical challenge to evaluate the
elements of the inverse (M
F
)
−1
φ during the updating process of the field φ.
EXERCISE
7.2 The Average Link Value
Problem. Calculate the average link variable
U =
+
dUU e
β
N
Re tr UW
+
dU e
β
N
Re tr UW
(1)
for the gauge group SU(2).
Solution. Since the trace of an SU(2) matrix is real, which can be understood
directly from (7.54), parameterize the SU(2) group elements with the help of the
Pauli matrices:
U = x
1
11 +i
i
x
i
σ
i
. (2)

7.1 Lattice QCD Calculations 471
Exploiting this property we can write the exponent in the exponentials of (1)
simply as β/2tr UW . A sum of SU(2) matrices is again proportional to a SU(2)
matrix:
i
U
i
= c
˜
U . (3)
This behavior becomes clear when remembering our discussion of Sect. 7.1.5.
There we showed that a SU(2) matrix corresponds to a unit vector on the hyper-
sphere S
3
. Adding several SU(2) matrices together is like adding several vectors,
the resulting vector pointing to the hypersurface, albeit with a different length.
Note that this behavior is very specific to the SU(2) group and cannot be applied
to SU(3). Using this feature we get
W = λV , V ∈ SU(2), λ=
√
det W . (4)
The invariance of the measure with respect to the variable change U → UV
+
yields
U =
+
dUU e
β
2
λ tr UV
+
dU e
β
2
λ tr UV
=
+
dUUV
†
e
β
2
λ tr U
+
dU e
β
2
λ tr U
= V
†
+
dUU e
β
2
λ tr U
+
dU e
β
2
λ tr U
. (5)
Let us first evaluate the denominator of (1):
dU e
β
2
λ tr U
=
1
4π
2
dϕ dΩ(n) sin
2
ϕ
2
exp
α
2
sin ϕ
sin
ϕ
2
≡ I ,α≡ βλ .
(6)
The integration over the solid angle dΩ can be directly performed, yielding
a value of 4π. Using the relation
sin ϕ = 2sin
ϕ
2
cos
ϕ
2
(7)
we get
I =
1
π
dϕ sin
2
ϕ
2
e
α cos
ϕ
2
=
1
π
1 −
∂
2
∂α
2
2π
0
dϕ e
α cos
ϕ
2
7 89 :
≡A
. (8)
Exercise 7.2

472 7. Nonperturbative QCD
Exercise 7.2
We can evaluate the integral A explicitly:
A =
∞
k=0
α
k
k!
2π
0
dϕ cos
k
ϕ
2
=
∞
k=0
α
k
k!
2
π
0
dφ cos
k
φ
=2
∞
k=0
α
k
k!
1
2
k
∞
l=0
k
l
π
0
dφ cos((k −2l)φ)
=2
∞
k=0
α
k
k!
1
2
k
∞
l=0
k
l
#
π if k = 2l
0otherwise
. (9)
Thus only terms with k even contribute to the sum:
A = 2
∞
µ=0
α
2µ
(2µ)!
1
2
2µ
2µ
µ
π
=2π
∞
µ=0
α
2µ
(2µ)!
1
2
2µ
(2µ)!
(µ!)
2
=2π
∞
µ=0
α
2µ
(µ!)
2
2
2µ
=2πI
0
(α) . (10)
The sum corresponds to the series representation of the Bessel function I
0
(x) of
the 2nd kind and 0th order. In general, the following relation for Bessel functions
holds:
11
I
m
(x) =
∞
k=0
1
k!(k +m)!
x
2
2k+m
. (11)
For the next steps we can make use of the following recursion relations for Bessel
functions:
I
m−1
(x) −I
m+1
(x) =
2m
x
I
m
(x),
I
m−1
(x) +I
m+1
(x) = 2I
m
(x),
I
0
(x) = I
1
(x). (12)
It follows that
I = 2
1 −
∂
2
∂α
2
I
0
(α)
11
e.g. see M. Abramowitz, I.A. Stegun: Handbook of Mathematical Functions (Dover
1968) Formula (9.6.10).
7.1 Lattice QCD Calculations 473
=2
I
0
(α) −
∂
∂α
I
1
(α)
=2
I
0
(α) −
I
0
(α) +I
2
(α)
2
= I
0
(α) −I
2
(α)
=
2
α
I
1
(α) . (13)
Now we have to compute the numerator of (1)
dUU e
βλ
2
tr U
(14)
=
1
4π
2
dϕ dΩ(n) sin
2
ϕ
2
cos
ϕ
2
+
i
2
sin
ϕ
2
n ·τ
exp
α
2
sin ϕ
sin
ϕ
2
.
Because
dΩ(n)n =0 , (15)
only the first term in the sum contributes:
1
π
2π
0
dϕ sin
2
ϕ
2
cos
ϕ
2
e
α cos
ϕ
2
=
1
π
∂
∂α
−
∂
∂α
3
2π
0
dϕ e
α cos
ϕ
2
=
1
π
∂
∂α
−
∂
∂α
3
2πI
0
(α)
= 2
I
1
(α) −
∂
∂α
#
I
0
(α) +I
2
(α)
2
&
= 2I
1
(α) −I
1
(α) −
I
1
(α) +I
3
(α)
2
=
2
α
I
2
(α) . (16)
Putting the results together we have determined the value of the average link:
U = V
†
2
α
I
2
(α)
2
α
I
1
(α)
= V
†
I
2
(α)
I
1
(α)
= (det W )
−1/2
W
†
I
2
(β
√
det W )
I
1
(β
√
det W )
. (17)
Exercise 7.2

474 7. Nonperturbative QCD
7.1.12 Strong and Weak Coupling Expansions
In the real world of low-energy QCD, lattice or continuum, analytical or semi-
analytical studies are usually not manageable. One can still get more understand-
ing of the behavior of the theory by tuning parameters to unphysical regimes.
In the lattice QCD action (7.48), neglecting fermionic effects for now, we have
one parameter β proportional to the inverse coupling squared. What happens
to observables when β is tuned to very small (strong coupling) or large (weak
coupling) values?
For that we consider one basic and useful quantity: the averaged plaquette
P, (7.39), which is directly connected to the QCD action as can be seen from
(7.48). In the limit of infinite coupling, β = 0, the weighting factor e
−S
vanishes,
which means that all link values occur with equal probabilities and the value of
the plaquette averages out to zero. In the opposite limit β →∞the exponential
weighting factor suppresses all contributions but the one with minimum action
S = 0, which means all U
µ
are equal to 1 up to a gauge transformaton. Thus
P=1 attains the maximum value.
Now let us go a step further and first calculate deviations from P=0for
small values of β analytically:
¯
P ≡
1
3
Re[trP]= Z
−1
1
n
P
[dU]
1
3
Re tr
(U
1
U
2
U
3
U
4
)e
−S[U]
(7.143)
n
P
is the number of plaquettes on the lattice, which is the number of independent
planes in the hypervolume (i.e. [(x, y), (x, z), (x, t), (y, z), (y, t), (z, t)]) times
the number of lattice points n
P
= 6N
3
x
N
t
. The shortcut
denotes summation
over all plaquettes on the lattice and the product of links encircles an elementary
square.
We perform a Taylor expansion of (7.143) to first order in β:
¯
P =
1
3n
P
[dU]
Re tr(U
1
U
2
U
3
U
4
7 89 :
P
)
1 −β
1
3
Re trP
×
'
[dU]
1 −β
1 −
1
3
Re trP
(
−1
, (7.144)
where we inserted the normalization factor in lowest-order β expansion.
In order to evaluate (7.144), one needs some basic integrals over the group
elements. The following relations hold (see Sect. 7.1.5):
[dU]=1 ,
[dU]U
ij
= 0 ,
[dU]U
ij
U
kl
= 0 ,
7.1 Lattice QCD Calculations 475
[dU]U
ij
U
∗
kl
=
1
3
δ
ik
δ
jl
. (7.145)
The first relation in (7.145) is the choice of normalization for the group integra-
tion. The second equation expresses the fact that a group element varied over the
whole group space vanishes. The first nontrivial relation is the last equation in
(7.145). You see that the nonvanishing contribution does not have an open color
index. This relates to our earlier discussion about gauge invariance, integrating
over quantities with open color averages out to zero. The factor 1/3 reads in
general 1/N
c
, the inverse number of colors.
With this set of integrals the integration of constants in the expression (7.144)
is trivial. The next terms of type
[dU]trP
=
[dU
1
dU
2
dU
3
dU
4
]tr(U
1
U
2
U
3
U
4
) = 0 (7.146)
vanish because according to (7.145) the integrals over terms linear in a given link
variable are zero.
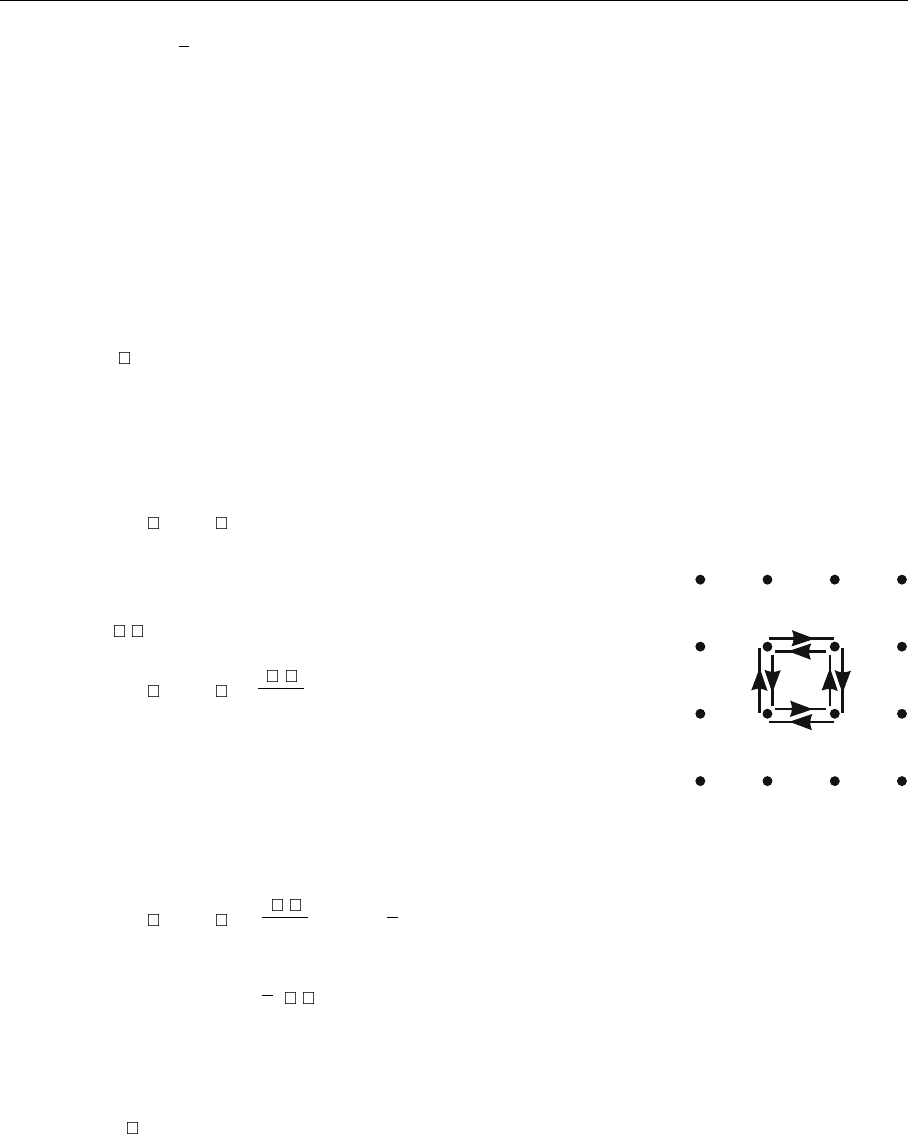
Nontrivial terms arise from the product of two plaquettes:
[dU]Re trP
Re trP
. (7.147)
If the two plaquettes and
were different, there would be link variables in
linear order contained in (7.147) and the integral vanishes. Therefore one obtains
a δ function δ
,
(see Fig. 7.5):
[dU]Re trP
Re trP
=
δ
,
4
dU
(1)
dU
(2)
dU
(3)
dU
(4)
×
U
(1)ij
U
(2) jk
U
(3)kl
U
(4)li
+h.c.
×
U
(1)i
j
U
(2) j
k
U
(3)k
l
U
(4)l
i
+h.c.
.
(7.148)
Using the relations (7.145) we get
[dU]Re trP
Re trP
=
δ
,
4
2
ijkl
i
j
k
l
1
3
4
δ
ii
δ
jj
δ
kk
δ
jj
=
1
2
δ
,
. (7.149)
Putting this all together we get the result for the denominator Z of (7.143),
Z = 1 −β
=1 −βn
P
, (7.150)
Fig. 7.5. The only nonvan-
ishing contribution for the
value of the plaquette oper-
ator in lowest order of the
coupling β: the product of
two elementary plaquettes
with opposite orientation

476 7. Nonperturbative QCD
and the expectation value of the plaquette in strong coupling approximation
reads
¯
P =
Z
−1
3n
P
⎧
⎨
⎩
β
3
−
1
2
,
δ
,
⎫
⎬
⎭
≡
Z
−1
18
β ∼
β
18
+O(β
2
). (7.151)
7.1.13 Weak-Coupling Approximation
Let us repeat the calculation of the plaquette value in the opposite regime of weak
coupling or large β. As we mentioned before, at large β the weight factor in the
path integral exp(−S({U})) picks out the contributions with small actions, and
in the extreme limit β →∞the configuration with S = 0 survives since the Wil-
son action is positive, S ≥ 0. With the definition of S, (7.48), this means all link
variables U
µ
= 1 (plus a possible gauge transformation; gauge transformations
do not change the value of the action) throughout the lattice and therefore we
also get trP=1. Calculating corrections in lowest order, 1/β, we proceed by
expanding the link variables about U =
11:
U = e
iλ
a
α
a
≈11 +iλ
a
α
a
(7.152)
and the product of links in the plaquette yields
P
=U
1
U
2
U
3
U
4
= e
iλ
a
α
a
1
· e
iλ
a
α
a
2
· e
iλ
a
α
a
3
· e
iλ
a
α
a
4
= e
iλ
a
"
a
+higher orders
=1 +iλ
a
"
a
−
1
2
λ
a
"
a
2
+O("
3
)
(7.153)
with "
a
=
4
i=1
α
a
i
. The normalizing factor (or partition function) Z in (7.143)
then gives
Z =
[dU]exp
−β
1 −
1
3
Re tr
1 −iλ
a
"
a
−
1
2
(λ
a
"
a
)
2
=
[dU]exp
−
β
6
tr(λ
a
"
a
)
2
. (7.154)
Using the relation tr λ
a
λ
b
=
1
2
tr {λ
a
,λ
b
}=2δ
ab
,weget
Z =
[dU]exp
−
β
3
"
a
"
a
. (7.155)

7.1 Lattice QCD Calculations 477
We do not really need the exact values of this expression but merely its β de-
pendence. Let us rescale all the parameters in the link variables α
a
→
˜
α
a
/
√
β.
[dU] contains 8 colors times 4 directions times (N
x
)
3
N
t
space–time points. Fol-
lowing the discussion in the continuum case (see Sect. 2.2.5) one can reduce
the number of gluonic degrees of freedom from 4 to 3 directions by specify-
ing a gauge. Gauge degrees of freedom leave the action invariant and therefore
would not contribute to the Gaussian integration in (7.155), i.e. they do not
generate a β-dependent term. Altogether we then get
Z = β
−12N
3
x
N
t
[d
˜
U]e
−
1
3
˜
"
a
˜
"
a
= const.β
−12N
3
x
N
t
. (7.156)
The plaquette can be calculated by taking a derivative of Z with respect to β:
N
−1
c
trP = 1 −
1
6N
3
x
N
t
∂
∂β
Z
Z
=1 −
2
β
+O
1
β
2
. (7.157)
7.1.14 Larger Loops in the Limit of Weak and Strong Coupling
In addition to calculating the plaquette analytically in the case of extreme coup-
ling, we can do a similar calculation in the case of larger Wilson loops. This
is especially interesting because of the connection between the Wilson loops
and the quark potential, which will be discussed in Sect. 7.1.15. The calcula-
tion is performed in the same way as in the previous section. The value of the
rectangular loop with sides of length L, L
is given by
w(l = (L, L
)) =
1
Z
[dU]e
−S
1
3
tr
;
l
U
l
. (7.158)
where
<
l
U
l
symbolizes the product of link variables around a closed loop l.
Obviously the plaquette and w are connected via trP = w(1, 1). Again we will
consider only lowest-order contributions in β. From the set of integrals (7.145),
we see that the only nonvanishing terms after integration contain for every link U
in the loop the oppositely oriented link U
†
, which comes from the plaquette
contained in the action S.
Now we can construct the relevant term diagramatically in similar ways as
shown in Fig. 7.4. Let us have a look at Fig. 7.7. The big loop is the Wilson loop
whose expectation value we want to calculate. By expanding the action in powers
of β we generate factors proportional to the plaquette operator (or 1 ×1 Wilson
loop). As is clear from the integrals (7.145) and (7.148) the plaquettes have to
compensate for the links in the loop by the conjugate links. Therefore you get
the inner circle of plaquettes (one wants to use the least number of elementary
loops because each one contains a factor β).
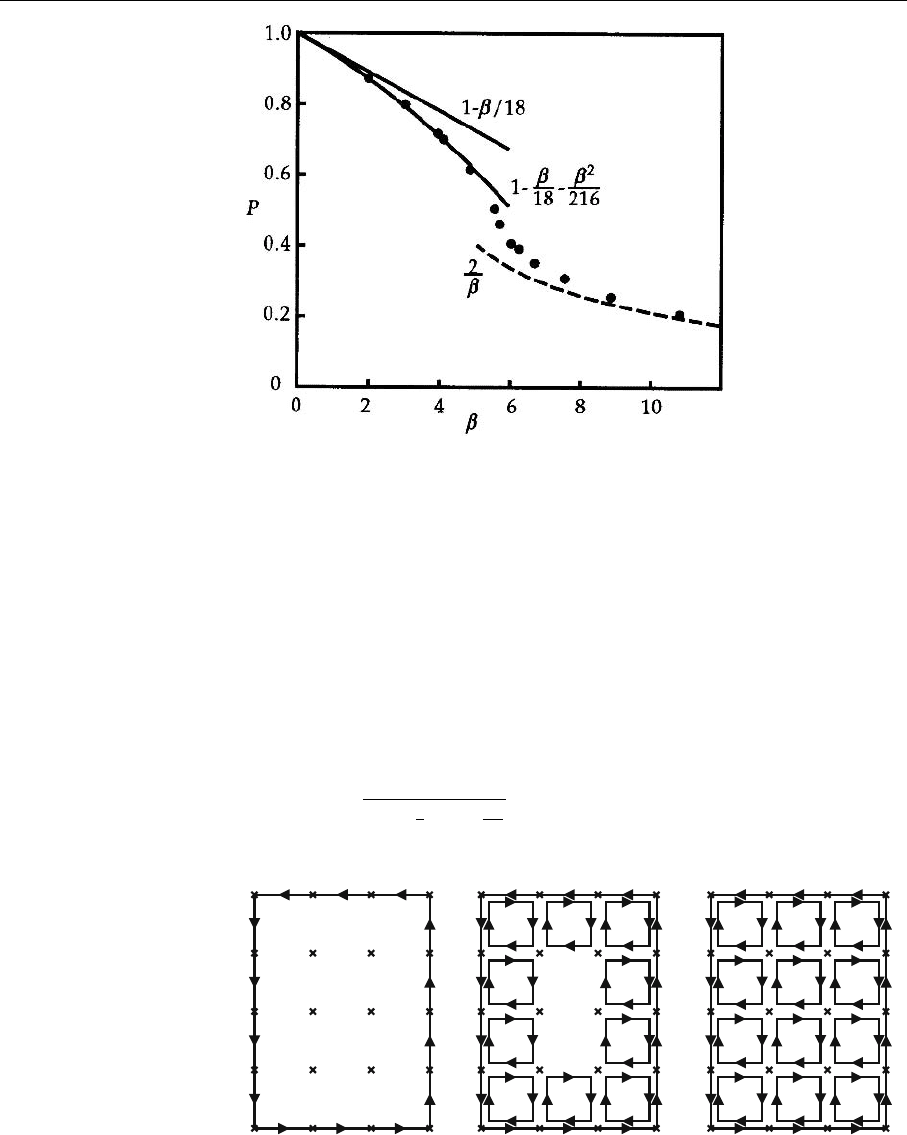
478 7. Nonperturbative QCD
Fig. 7.6. Monte Carlo re-
sults for the expectation
value of the plaquette. One
can identify the results of
strong (7.151) and weak
coupling (7.157). The nu-
merical data are taken from
M. Creutz: Quarks, Gluons,
and Lattices, Cambridge
University Press, Cambridge,
1983
Fig. 7.7. The 3×4 Wilson
loop w(3, 4). The interior is
filled up with plaquettes suc-
cessively, matching each oc-
curring link variable with an
analogous link pointing in
the opposite direction
Since there are in general some additional unsaturated links from the plaque-
ttes, one has to fill up the remaining holes with additional plaquettes. This then
finally yields the nonvanishing contribution to the Wilson loop in lowest order
in β.
As we mentioned before, every plaquette contains a factor β. One can infer
from Fig. 7.7 that the first contribution to w(L, L
) is proportional to β
L·L
. Thus,
we are left calculating the coefficient in front of β
L·L
.
From a perturbation theory point of view the introduction of a cutoff scale a
is just another method of regularization of QCD. Gauge invariance arguments
yielded a general formula for the running coupling constant in lowest-order loop
calculation (see Sect. 4.4):
g
2
(Q
2
) =
16π
2
(11 −
2
3
N
f
) ln
Q
2
Λ
2
. (7.159)

7.1 Lattice QCD Calculations 479
The asymptotic scale parameter Λ depends on the regularization scheme. In lat-
tice perturbation theory the momentum scale is therefore Q = 1/a. Thus for
sufficiently dense lattices the coupling strength depends on the lattice spacing
as
g
2
(a) =−
16π
2
(11 −
2
3
N
f
)ln(a
2
Λ
2
lat
)
, (7.160)
where Λ
lat
is the scale parameter corresponding to a renormalisation scheme
based on an Euclidean lattice. This parameter can be obtained only by actually
solving the corresponding Feynman diagrams in the lattice formulation. This is
a very complex calculation.
12
Compared to continuum renormalisation schemes,
e.g. the momentum-subtraction scheme (MOM), we have Λ
lat
∼ 0.012 Λ
MOM
,
a very small number.
This has the consequence that one needs lattices with very small a (i.e. with
many lattice points) to be in a regime where quantities measured on a lattice
change only perturbatively when one changes the lattice spacing (the so-called
scaling limit). So far lattice calculations have not yet reached this regime.
7.1.15 The String Tension
A very important quantity is the string tension σ. Its value of about 1 GeV/fm
is often used as a scale or measure of calculated quantities in QCD. As will be
argued in this section the potential between a quark and an antiquark V
QQ
(R)
is expected to grow linearly with distance. This can be readily understood
by assuming a flux tube model connecting the quark and antiquark, where the
color-electric field lines are confined in a tubelike connection between the two
quarks. No field lines leak out of the tube, therefore the field strengths remain
constant over the extension of the tube and the potential rises linearly with the
distance of the quarks. Thus we have
V
QQ
(R)
R→∞
−→ σR . (7.161)
Here one additionally assumes heavy quarks in order to apply the nonrelativistic
concept of a quark potential. This expected behavior is a basic but crucial testing
ground for lattice QCD.
As mentioned, we assume static, i.e. very heavy, quarks. Then their kinetic
energy vanishes. They sit at some given point and propagate in time only. Keep-
ing in mind that for the Euclidean action the potential enters with a positive sign,
the action is then merely
S
E
Q
Q
=
τ
f
τ
i
dτV
QQ
(R
QQ
) = TV(R), (7.162)
12
see e.g. P. Weisz: Phys. Lett. B 100, 330 (1981).
