Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


450 7. Nonperturbative QCD
the coupling constant into the field in order to follow standard notation of lattice
gauge theory. Except for the matrix structure the formulae look like expressions
in QED (by keeping in mind that the covariant derivative for electrons in QED
reads D
µ
=∂
µ
+ieA
µ
(x) as the charge of the electron is defined to be negative).
In fact, although the phenomenology is very different, most of the relations that
will be derived in this chapter can be directly applied to the U(1) gauge group
of QED. The first term in D
µ
is the standard translational operator which is di-
agonal in color space. The second term, containing the gluon field, describes the
actual color transport between the infinitesimally close points x and x+dx.We
concentrate on the parallel transport of the color orientation. We have a factor
(1 +i
ˆ
A
µ
(x) dx
µ
) (7.26)
in (7.25). When we look at color transport between two neighboring points x and
x +ae
µ
in some direction µ on the lattice, we apply the infinitesimal color trans-
lation infinitely many times along a straight path connecting the points. We get
(no summation over µ) an infinite product of small displacement factors (7.3)
along the line between x and x +ae
µ
:
lim
N→∞
N−1
;
n=0
1 +i
ˆ
A
µ
(x +nδx)∆x
µ
ˆ
A
µ
= P exp
⎛
⎜
⎝
i
x+ae
µ
x
ds
µ
ˆ
A
µ
(x)
⎞
⎟
⎠
≡U
µ
(x), (7.27)
with small steps ∆x
µ
=ae
µ
/N, letting the number of steps N go to infinity.
A line integral connecting the initial and final points enters the expression (7.27).
The symbol P denotes path ordering −the multiplication of the gauge field ma-
trices is ordered along the path as is also obvious from the ordering of the terms in
the product of the first line of the equation. The quantity U
µ
(x), which connects
two neighboring points on the lattice, is called the link variable. From (7.27)
it becomes clear that the link variable that transports color from x +ae
µ
to x,
U
−µ
(x +ae
µ
) is directly related to U
µ
(x) via the relation
U
−µ
(x +ae
µ
) = U
†
µ
(x). (7.28)
In the standard formulation of lattice QCD the link variables are chosen as the
basic variables for the gluons instead of the usual gauge potentials
ˆ
A
µ
(x).For
every point on the lattice there are four link variables. Therefore the number of
degrees of freedom of the fields remains unchanged when switching to the new
variables. We will see in the course of this chapter why this change in variables
is useful for lattice formulations.

7.1 Lattice QCD Calculations 451
7.1.4 Gluons on the Lattice
In the following, we will derive the discretized counterpart of the gluonic action
in the continuum
5
S
E
=
1
2g
2
tr
d
4
xF
µν
(x)F
µν
(x)
, (7.29)
where, as in the previous section, we adopt the Euclidean formulation of the the-
ory. As we discussed in Chap. 4 the action (and the Lagrange density) is gauge
invariant. Adopting gauge invariance as the construction principle for the ac-
tion, we will formulate the most simple nontrivial gauge invariant expression on
the lattice by using the link variables (7.27), which we introduced previously.
In order to perform this task we first have to determine the gauge properties of
the link variable itself. If the lattice spacing a is very small one can approximate
a single link U
µ
(x), pointing in the direction µ,by
U
µ
(x) ≈ 1 +iaA
µ
(x). (7.30)
However, even if a is not small enough for (7.30) to be a good approximation,
one can divide the integral over the path between x and x +ae
µ
,wheree
µ
is the
unit vector in the µ direction, into many (N )smallsteps" = a/N and repeatedly
apply (7.30):
U
µ
(x) ≈ exp(i" A
µ
(x)) exp(i"A
µ
(x +"e
µ
)) ···exp(i"A
µ
(x +(a −")e
µ
)) .
(7.31)
Note that we have exploited the fact that the definition of U
µ
contains path or-
dering, which is the reason why we could write (7.31) as successive products of
exponentials along the path. For a single factor in (7.31) we can now use the form
(7.30):
δU
µ
(x) ≡ exp
i
a
N
A
µ
(x)
≈ 1 +i"A
µ
(x). (7.32)
For the gauge-transformed δU
µ
(x) we have
δU
µ
(x) ≈ 1 +i"A
µ
(x), (7.33)
which, according to (4.55), reads
δU
µ
(x) ≈ 1 +i"g(x)A
µ
(x)g
+
(x) +"(∂
µ
g(x))g
+
(x), (7.34)
where g(x) is a SU(3) gauge transformation at point x. Equation (7.34) can be
rewritten as
g(x) +"∂
µ
g(x)
1 +i" A
µ
(x)
g
+
(x) +O("
2
)
= g(x +"e
µ
) exp(i" A
µ
(x))g
+
(x). (7.35)
5
Note that all the colored quantities, the gauge field A
µ
, the field strength F
µν
,the
link variable U
µ
, and the gauge rotation g are 3 ×3 matrix-valued fields. To prevent
cluttering of the text with too many symbols, we will suppress the ˆ symbol in the
formulae.

452 7. Nonperturbative QCD
i
m
U(x)
m i
U(x+ae)
-mmi
Fig. 7.3. The most simple
(and trivial) two-link gauge-
invariant object
x
n
m
Fig. 7.4. Plaquette P
µν
(x) in
the plane (µν) first nontriv-
ial gauge-invariant term
Inserting this expression into (7.33), we finally get
U
µ
(x) = g(x +e
µ
)U
µ
(x)g
+
(x). (7.36)
This transformation property of the link variable is quite plausible (much more
so than (4.55)). The link variable transports color from one point to the next and it
transforms via a color rotation at the initial point and another (inverse) rotation at
the final point. This form of gauge transformation also suggests the construction
principle of a gauge invariant term. One has to build a product of link variables
that are connected in space–time and do not carry an open color index (color
singlet). The most simple object is shown in Fig. 7.3. It can be written as
tr
U
µ
(x
i
)U
−µ
(x
i
+ae
µ
)
. (7.37)
Unfortunately, using (7.28) we get
tr
U
µ
(x
i
)U
µ
(x
i
+ae
µ
)
= tr
U
µ
(x
i
)U
+
µ
(x
i
)
= tr
[
11
]
=3 , (7.38)
which is a (trivial) constant. The first nontrivial expression is shown in Fig. 7.4.
It is a product of four links encircling an elementary square of four neighboring
points in a plane on the lattice. It is also called plaquette P
µν
:
P
µν
(x) =
U
µ
(x)U
−ν
(x +ae
ν
)U
−µ
(x +ae
µ
+ae
ν
)U
ν
(x +ae
µ
)
=
U
µ
(x)U
+
ν
(x)U
+
µ
(x +ae
ν
)U
ν
(x +ae
µ
)
. (7.39)
One can directly check that the expression tr(P
µν
) is gauge invariant by
inserting the gauge-transformed links into (7.39):
tr
P
µν
(x)
=tr
U
µ
(x)
U
ν
(x)
+
U
µ
(x +e
ν
)
+
U
ν
(x +e
µ
)
=tr
g(x +e
µ
)U
µ
(x)g
+
(x)g(x)U
+
ν
(x)g
+
(x +e
ν
)
× g(x +e
ν
)U
+
µ
(x +e
ν
)g
+
(x +e
ν
+e
µ
)
×g(x +e
µ
+e
ν
) U
ν
(x +e
µ
)g
+
(x +e
µ
)
(7.40)
and by permuting the terms in the trace. This immediately yields
tr
P
µν
(x)
= tr
P
µν
(x)
. (7.41)
In the next step we have to find the continuum analogue of the plaquette, i.e. we
calculate
P
µν
(x), a → 0 . (7.42)
Let us first consider the links in the plaquette separately. Assuming that a is suf-
ficiently small we approximate the line integral in the links as in (7.32). We take
the value of A
µ
(x) in the middle of the line
U
µ
(x) ≈ exp
iaA
µ
(x +ae
µ
/2
≈exp
ia
A
µ
(x) +a/2∂
µ
A
µ
(x)
(no summation over µ!), (7.43)
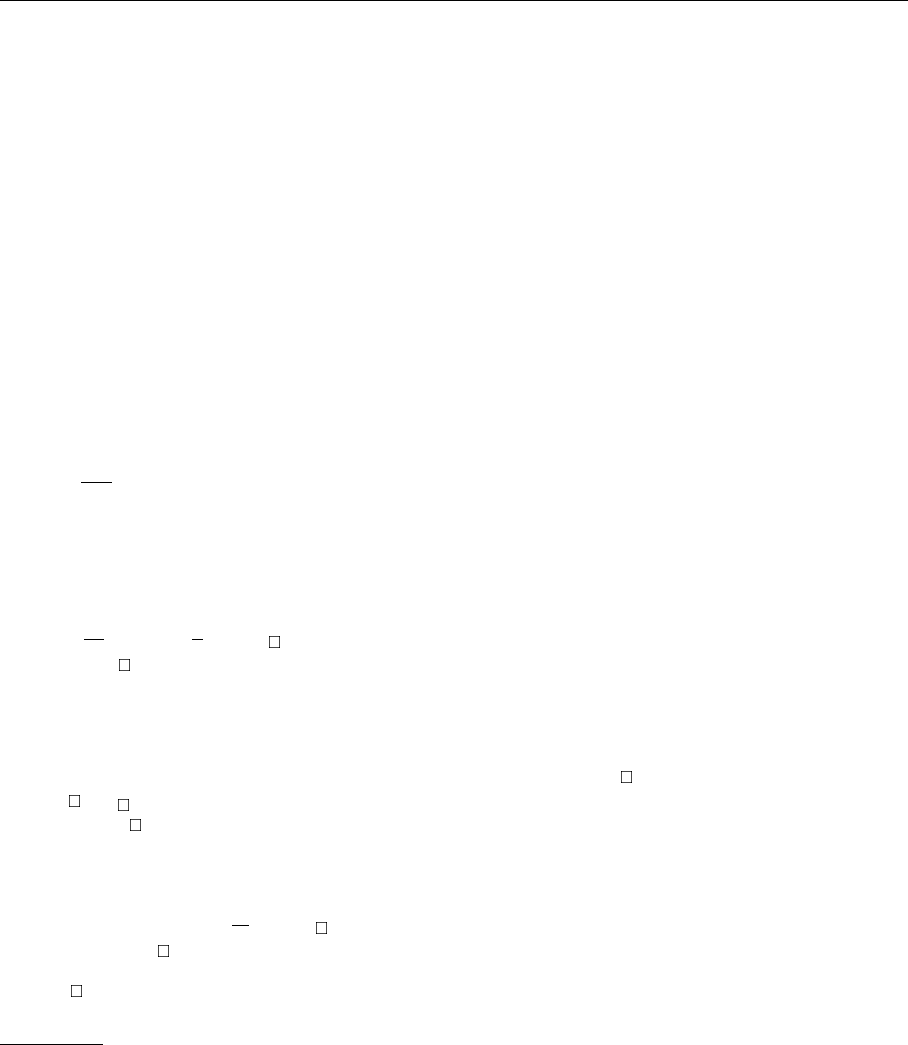
7.1 Lattice QCD Calculations 453
U
+
ν
(x) ≈exp
(
−ia
[
A
ν
(x) +a/2∂
ν
A
ν
(x)
]
)
,
U
+
µ
(x +e
ν
) ≈ exp
−iaA
µ
(x +a(e
ν
+e
µ
/2))
,
≈exp
−ia
A
µ
(x) +a∂
ν
A
µ
(x) +a/2∂
µ
A
µ
(x)
,
U
ν
(x +e
µ
) ≈ exp
ia
A
ν
(x) +a∂
µ
A
ν
(x) +a/2∂
ν
A
ν
(x)
. (7.44)
The products of the links yield
U
µ
(x)U
+
ν
(x)U
+
µ
(x +e
ν
)U
ν
(x +e
µ
)
≈exp
ia
2
∂
µ
A
ν
(x) −∂
ν
A
µ
(x)
+a
2
A
µ
(x), A
ν
(x)
. (7.45)
Comparing the exponent of this expression with the definition of the non-Abelian
field strength tensor F
µν
, in (4.58), we have
P
µν
(x)
a→0
=
exp
ia
2
F
µν
(x)
. (7.46)
The continuum action for the gluons is (7.29)
S
E
C
=
1
2g
2
tr
d
4
xF
µν
(x)F
µν
(x)
. (7.47)
Comparing this expression with (7.46), we can construct the corresponding lat-
tice version S
E
W
(W for Wilson action) that coincides with the continuum action
in the limit of vanishing lattice spacing a:
S
E
W
=
6
g
2
1 −
1
3
Re tr( P
)
. (7.48)
The shortcut symbol
denotes a single elementary plaquette on the lattice. The
sum extends over all possible plaquettes of the four-dimensional lattice. There
are 6 planes in a 4-dimensional lattice,
6
thus there are 6(N
x
)
3
N
t
elementary
squares. Note that you can replace the real part of the trace by Re tr (P ) =
1/2tr (P
+ P
+
). The Hermitean conjugate of the plaquette can be seen as
the plaquette P with reversed orientation of the links (see Fig. 7.4). Expres-
sion (7.48) is called the Wilson action.
7
One can easily generalize (7.48) to an
arbitrary group SU(N)
S
E, SU(N)
W
=β
1 −
1
N
Re tr (P
)
, (7.49)
where P
now contains the appropriate unitary N ×N matrix-valued link vari-
ables. Many QCD lattice calculations use the SU(2) instead of the SU(3) group.
6
A plane is defined by two axes. There are four directions on the lattice, therefore there
exist six independent planes.
7
The coefficient in front of the sum is usually denoted as β = 6/g
2
for SU(3), or in
general β = 2N/g
2
for a SU(N) gauge group. It is the only free parameter of the theory.

454 7. Nonperturbative QCD
The advantage is that there are far fewer SU(2) gluons (3 compared to 8 in
SU(3)), which reduces the computational efforts considerably. Many features,
like asymptotic freedom and color confinement, exist already for SU(2). In the
following, we will also consider SU(2) several times for illustration.
7.1.5 Integration in SU(2)
In the expression for the path integral and for the observables calculated in the
path-integral formalism, (7.23), one has to perform the integration over the group
elements for every link on the lattice. We will show how this can be done for
the group SU(2), which is much more intuitive (and simpler) than in the case of
SU(3). The SU(2) link variables are unitary 2 ×2 matrices. One can parameterize
them in the form
U =
ab
−b
∗
a
∗
. (7.50)
The matrix fulfills the unitarity condition
U
+
U =1 (7.51)
if we demand that
|
a
|
2
+
|
b
|
2
= 1 (7.52)
holds. Instead of using complex parameters a,b we can also take real ones with
a = x
4
+ix
3
and b = x
2
+ix
1
. Then (7.52) reads
x
2
1
+x
2
2
+x
2
3
+x
2
4
=1 . (7.53)
Obviously, with this choice one can rewrite U also in a slightly different form.
Inserting the x components into (7.50) explicitly yields
U =
x
4
+ix
3
x
2
+ix
1
−x
2
+ix
1
x
4
−ix
3
, (7.54)
which one can rewrite with the help of the Pauli matrices (i = 1, 2, 3) as
U = x
4
11 +ix
i
σ
i
. (7.55)
Now, using (7.53) we write the group integration (integration over the group
elements) in the form
dU = N
d
4
xδ
x
2
1
+x
2
2
+x
2
3
+x
2
4
−1
. (7.56)
Thus the SU(2) integration can be rewritten as an integration over the surface of
the unit sphere S
3
in four dimensions. The normalization N is chosen such that
the basic integration over the group space returns 1:
dU = 1 ⇒ N =
1
+
d
4
xδ
(
x
i
x
i
−1
)
=
1
Ω
3
, (7.57)

7.1 Lattice QCD Calculations 455
where the surface Ω
3
of the hypersphere is Ω
3
=2π
2
. Going a step further, con-
sider the integration over one link. We take the single matrix element U
11
as an
example:
dUU
11
=
1
2π
2
d
4
xδ
|x|
2
−1
(
x
4
+ix
3
)
=0 . (7.58)
The integration over odd functions of x
i
vanishes:
dUU
ij
= 0 . (7.59)
An important integral is
dUU
ij
U
+
kl
. (7.60)
From the previous integral it is clear that integrals over functions of the type
U
11
(U
+
)
12
= (x
4
+ix
3
)(x
2
+ix
1
) vanish. The following integral is zero, too:
dUU
11
U
+
22
=
dUa
2
=
dU
x
2
4
−x
2
3
+2ix
3
x
4
= 0 . (7.61)
The integrals over x
2
3
and x
2
4
cancel. The third term vanishes following (7.59).
The only nonvanishing terms are proportional to |a|
2
, |b|
2
:
dUU
11
U
+
11
=
dU
x
2
3
+x
2
4
=
1
2π
2
1
2
d
4
x δ
x
2
i
−1
x
2
1
+x
2
2
+x
2
3
+x
2
4
=
1
2
(7.62)
and also
+
dUU
12
U
+
21
=
1
2
. Thus we have
dUU
ij
U
+
kl
=
1
2
δ
il
δ
jk
. (7.63)
The factor
1
2
normalizes the integral over the trace:
dU tr
UU
+
=1 , (7.64)
which holds for all SU(N). In (7.63) one has to replace
1
2
by
1
N
for the general
SU(N) result, accordingly. This is evident from (7.64). Rewriting the equation
in the form
dU tr
UU
+
=
i
dUU
ii
U
†
ii
=1 ,

456 7. Nonperturbative QCD
it necessarily follows that
dUU
ii
U
†
ii
=
1
N
,
since no direction in the group space is preferred.
7.1.6 Discretization: Scalar and Fermionic Fields
After introducing the idea of discretizing space and time on a rectangular equally
spaced lattice and introducing the link variables for the gauge fields, we will now
study the implementation of other field variables in such a system. We will first
look at the equations of motion for scalar particles and then discuss the important
case of spin-
1
2
particles that we require in order to treat quarks in the lattice cal-
culations. There are important differences between those cases which also have
to be dealt with in a lattice description of QCD. First, let us introduce the Fourier
transform of functions on our lattice. In one dimension the Fourier transform of
a function f(x
i
) defined on the lattice is
˜
f ( p) =
+∞
n=−∞
af(x
n
) exp(−i px
n
) with the discrete points x
n
=na .
(7.65)
(The spacing between neighboring points is again given by a.) As you can see
from this formula
˜
f ( p) is periodic:
˜
f ( p) =
˜
f
p +2
π
a
. (7.66)
We therefore restrict momentum integration to the range
(
−π/a,π/a
]
,which
is well known as the first Brillouin zone in solid-state physics. The inverse
transform is then
f(x
n
) =
π/a
−π/a
dp
2π
˜
f ( p) exp(i px
n
). (7.67)
The Kronecker symbol δ
nm
follows directly as
δ
nm
=
a
2π
π/a
−π/a
dp exp(i p(x
n
−x
m
)) . (7.68)
After having defined these preliminaries we can study the discretization of the
field equations of motion.
The (Euclidean) Klein–Gordon equation for a scalar particle reads
−m
2
Φ(x) =0 . (7.69)

7.1 Lattice QCD Calculations 457
We have to discretize the Laplace operator , i.e. the second derivatives acting
on the field. Again, as mentioned before, we study the system in the Euclidean-
time formalism, setting the g
µν
tensor to be δ
µν
. Using a 3-point formula for the
second derivative we get the equation
1
a
2
4
µ=1
Φ(x
n
−e
µ
) +Φ(x
n
+e
µ
)
−
8
a
2
+m
2
Φ(x
n
) = 0 (7.70)
for the field at point x
n
. We can rewrite the equation in matrix form:
G
−1
nm
Φ
m
=0 , (7.71)
where the matrix (G
−1
) is given by
G
−1
nm
=
1
a
2
)
µ
δ
n−µ,m
+δ
n+µ,m
−
8 +(ma)
2
δ
n,m
*
. (7.72)
This tridiagonal matrix is the inverse of the propagator of the particle. Using the
Fourier representation of the Kronecker δ
nm
, (7.68), we can calculate the propa-
gator of the Φ field in momentum space. Inserting (7.68) into (7.72) we read off
the result
G
−1
( p) = a
4
n,m
G
−1
nm
exp(−i p
µ
(x
n
−x
m
)
µ
)
=a
2
'
4
µ
sin
2
p
µ
a
2
+(ma)
2
(
. (7.73)
Remember, that the momenta can lie in the range −π/a ≤ p
µ
<π/a.Oneim-
portant point in the lattice description is the continuum limit of the theory. The
propagator has poles for momenta corresponding to the propagation of real par-
ticles. Except for the overall scale factor a
4
we can perform the continuum limit
of (7.73). We get
a
−4
G
−1
( p
µ
)
a→0
=
p
2
µ
+m
2
. (7.74)
The poles are at p
2
µ
=−m
2
(in Euclidean space–time!) as it should be. We can
write the propagator in space–time accordingly:
G
−1
(x
n
−x
m
) = a
2
d
4
k
(2π)
4
exp(ik(x
n
−x
m
))
4
µ
sin
2
ka
2
+(ma)
2
, (7.75)
with the obvious continuum limit a → 0,
G
−1
(x) =
d
4
k
(2π)
4
exp(ikx)
k
2
+m
2
. (7.76)

458 7. Nonperturbative QCD
Let us now move over to the discretization of the equations of motion for a spin-
1
2
field (a quark, for instance). The main difference from the previous case is that
the Dirac equation is a first-order differential equation. We have to discretize the
equation
(
p/ −im
)
ψ = 0 . (7.77)
The γ matrices fulfill the standard anticommutation relations
$
γ
µ
,γ
ν
%
=2δ
µν
, (7.78)
where we used the metric tensor in Euclidean space δ
µν
instead of the usual g
µν
.
We adopt the standard (but not unique) choice of γ matrices in Euclidean space:
γ
4
→γ
0
, γ → iγ
i
. (7.79)
As γ
0
is hermitian and the original γ are antihermitean, the newly defined γ
matrices are all hermitean. Inserting those matrices into the Dirac equation we
obtain
γ
µ
∂
µ
+m
ψ =0
⇐⇒
'
m
γ
µ
1
2a
ψ(x
n
+e
µ
) −ψ(x
n
−e
µ
)
+mδ
mn
(
ψ
m
= 0 . (7.80)
In matrix notation we get the inverse propagator
G
−1
αβ
n,m
=
1
2a
'
µ
δ
n,m+µ
−δ
n,m−µ
γ
µ
(
+mδ
n,m
δ
α,β
. (7.81)
Using expression (7.68) for δ
nm
we can derive the Fourier transform of the
inverse fermion propagator
G
−1
αβ
( p) =
1
a
'
i
µ
sin(p
µ
a)γ
µ
+ma
(
δ
αβ
. (7.82)
Now, the continuum limit is more tricky in the case of spin-
1
2
particles compared
to the spin-0 case, or in general, for fermions as opposed to bosons. In the limit
a → 0, we get the standard result from (7.82):
G
−1
a→0
∼ (i p
µ
γ
µ
+m)δ
αβ
, (7.83)
which is just the usual (Euclidean) Dirac equation. However, this is not the end
of the story. The momenta p
µ
vary between −π/a and π/a. Usually, assuming
a massless field for simplicity, the root of (7.83) is the single on-shell condi-
tion p
2
µ
=0. However, sin( p
µ
a) also vanishes at the edge of the Brillouin zone
with p
µ
=±π/a. We end up with an additional pole, or particle, at π/a (if the
Brillouin zone is defined to be a closed interval at that point). This effect is the
7.1 Lattice QCD Calculations 459
so-called fermion-doubling problem. In one dimension we have two poles in the
propagator. In the case of two dimensions we therefore have 2
4
=16 “particles”
instead of 1. Where did this problem originate from? The trouble started with the
symmetric first-order discretized derivative, (7.80), which leads to the fact that
the argument of the sine is ( p
µ
a) instead of ( p
µ
a/2) for spin-0 particles. It is
the linear nature of the Dirac equation that generates doublers in its discretized
version.
There are a number of methods to deal with fermion doubling. We will dis-
cuss the two most common methods to remove the superfluous solutions. The
first method was originally proposed by Wilson, like most of the first concepts
in lattice gauge theory. One adds an additional term to the equations of motion
−
r
2
ψ(x) to the Dirac equation:
γ
µ
∂
µ
+m −
r
2
∂
µ
∂
µ
ψ(x) =0 (7.84)
with some parameter r, also often called the Wilson parameter. This equation is
discretized on the lattice as usual, where we take the second derivative in (7.81)
from (7.70). Thus we get the matrix equation
G
−1
mn
ψ
n
= 0 (7.85)
with
G
−1
mn
=
1
2a
µ
(γ
µ
−r)δ
m,n+µ
−(γ
µ
+r)δ
m,n−µ
+
m +4
r
a
δ
m,n
11 . (7.86)
Fourier transforming (7.86) the inverse propagator reads
G
−1
( p) =
i
a
γ
µ
sin(p
µ
a) +m +2
r
a
µ
sin
2
p
µ
a
2
. (7.87)
As you can see from (7.87) in the continuum limit, a → 0, the additional term
vanishes like a
1
. However, at the corner of the Brillouin zone p =±π/a the fac-
tor does not vanish because of the
1
2
in the argument of the sine function. The
term therefore diverges like 1/a effectively generating an infinite mass for the
fermion doublers. Including the gluons, (7.86) then reads
M
F
mn
(U) ≡
G
−1
(U)
mn
=
1
2a
µ
γ
µ
−r
U
m
u(x
n
)δ
m,n+µ
−(γ
µ
+r)U
+
µ
(x
m
)δ
m,n−µ
+
m +4
r
a
δ
m,n
11 . (7.88)
Fermions which obey (7.86) are called Wilson fermions. Wilson fermions are
still widely used in lattice gauge calculations of QCD. One problem connected
