Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

6.2 Small-x Physics 439

than the leading-order result.

This situation is not yet understood. Argu-

ments exist that a complete resummation of various terms would lead to a more

acceptable picture or that additional nonperturbative input is needed.

Refering to the leading-order result for the pomeron intercept as it follows

from the BFKL equation

12α

ln(2), (6.98)

the corrected (NLO) intercept ω

can be written as

= ω



1 −





4ln(2)



= ω



1 −2.4ω



, (6.99)

where r





is the eigenfunction of the BFKL kernel with the largest eigen-

value (for details see the original literature

). Discarding details, even if the

coefﬁcient 2.4 looks not very large, since ω

itself is not small, the NLO result

completely cancels the leading-order one. For example, if α

=0.15, where the

Born intercept is ω

=12α

ln(2) = 0.397, the relative correction for n

= 0is

big:

= 1 −r

·3 = 0.0747 . (6.100)

Whether the NNLO calculation or partial resummation of big corrections will be

able to cure this problem remains to be seen.

V. Fadin and L. Lipatov: Phys. Lett. B 429, 127 (1998),

G. Camici and M. Ciafaloni: Phys. Lett. B 430, 349 (1998).

7. Nonperturbative QCD

In the previous chapters we discussed mainly QCD effects as calculated in

perturbation theory. We found reasonable agreement between the general the-

ory of strong interaction and experimental results in high-energy scattering.

However, there are other regimes in QCD that are much harder to treat the-

oretically. This problem had already been illustrated in Example 4.4. In fact,

as can be seen in Fig. 4.8, the running coupling constant α(q

) increases at

small momentum transfers, reaching a value comparable to 1 at momenta q

around

|∼500 MeV. Obviously a power-series expansion in a quantity of

the order of one does not converge: α ≈ α

. Feynman graphs with many vertices

(Fig. 7.1a) have an expansion coefﬁcient of the same order as the most simple

ones that carry only one vertex.

qqqq

(a) (b)

Fig. 7.1a,b. Feynman dia-

gram for quark–quark inter-

action: (a) complicated glu-

onic exchange; (b) simple

one-gluon exchange. In the

low-momentum regime pro-

cess (a) is not suppressed

compared to (b) due to the

break downof the perturba-

tion expansion, yielding an

inﬁnite number of relevant

diagrams that (in principle)

need to be computed

This leads us to the general problem that QCD at small momenta or ener-

gies E ≤ 1 GeV has to be treated nonperturbatively. The properties of a proton,

for instance, with a mass of M

=938.3MeV/c

are in this regime. Therefore,

if we want to understand protons (and, in fact, all hadrons), perturbation theory

won’t be of help and another approach has to be found. Nonperturbative sys-

tems are inherently difﬁcult to treat, and there are generally no simple systematic

methods available for solving them. In the course of this chapter we will look at

two very different ways to tackle this problem: lattice gauge theory and sum rule

techniques.

442 7. Nonperturbative QCD

7.1 Lattice QCD Calculations

The idea of calculating QCD numerically on a lattice is directly tied to the

path-integral or functional-integral representation of quantum mechanics and

quantum ﬁeld theory. Before continuing further with the derivation of the QCD

Lagrangian on the lattice we will ﬁrst discuss some basic notions of the method

of path integration in order to provide the reader with some understanding of the

background of the lattice formulation. A much more detailed discussion of this

topic can be found in the book on ﬁeld quantization.

7.1.1 The Path Integral Method

Let us consider a particle propagating from a starting point x

at time t

to a point

). For a given (not necessarily classical) trajectory x(t) and

x(t) of the par-

ticle connecting the initial and ﬁnal points we may determine the corresponding

action S given its Lagrangian L:

S =

dtL

[

x(t),

x(t)

]

. (7.1)

The action S depends on the position x(t) and the velocity

x(t) along the path.

As we are discussing quantum mechanics the connecting path does not have to

be the solution of the classical equations of motion. The path integral method,

largely developed and propagated by Feynman following earlier ideas of Dirac,

states that the total probability amplitude of the transition of the particle from

) to x

) can be described by a weighted sum over all possible trajectories

(paths P) x

between those two points:

x

)|x

)∼



paths(x

)

exp(iS(

{

x(t),

x(t)

}

)) . (7.2)

We approximate the time evolution of the system, discretizing the time coordi-

nate into N −1 intermediate time slices t

(n = 1,...,N −1):

∆t =

−t

= t

+n∆t . (7.3)

W. Greiner and J. Reinhardt: Field Quantization (Springer, Berlin, Heidelberg 1996).

P.A.M. Dirac: Physikalische Zeitschrift der Sowjetunion 3, 64 (1933). Also see

the monograph by R. P. Feynman and A. R. Hibbs: Quantum Mechanics and Path

Integrals (McGraw-Hill, 1965).

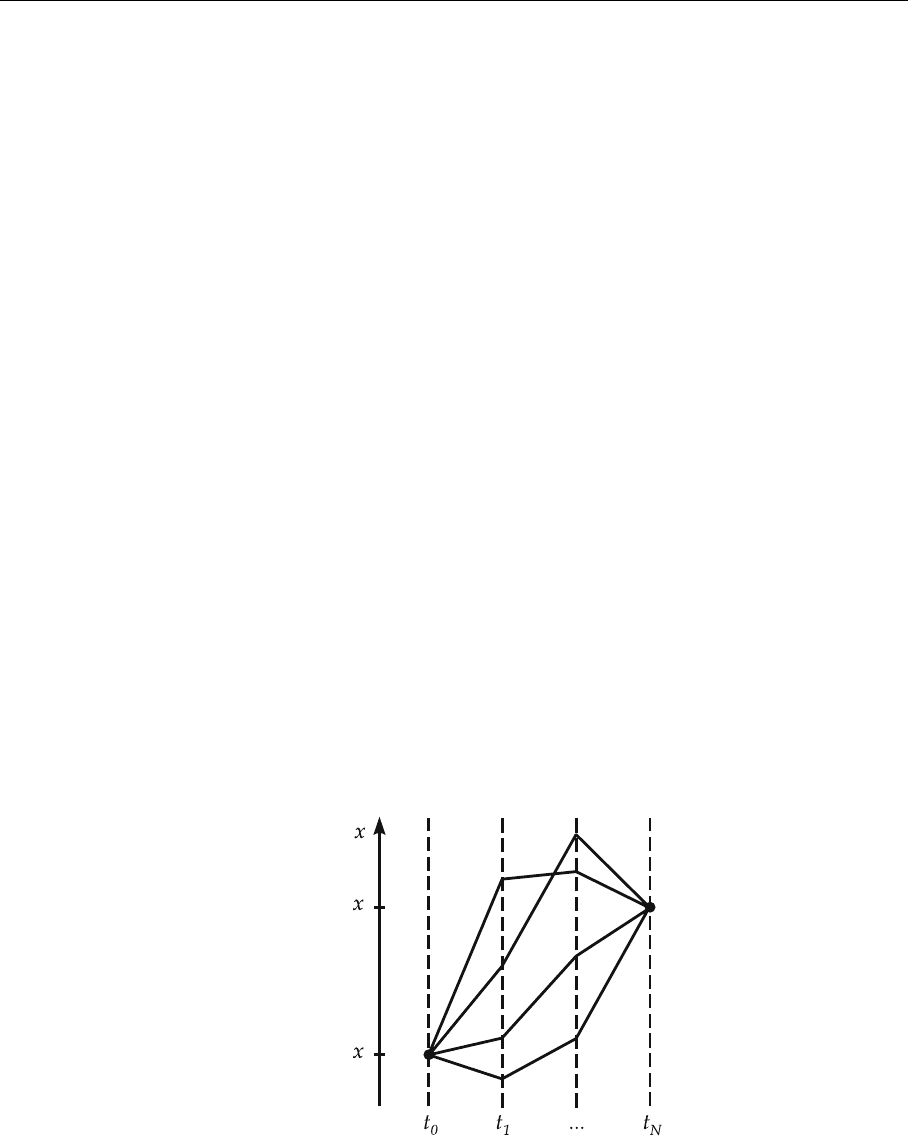
7.1 Lattice QCD Calculations 443

One can now ‘sum’ over the trajectories at the different time slices. The sum over

the paths P at a speciﬁc time t

is given by



P(t=t

)

exp(iS(

{

x(t

)

}

)) ∼

∞

−∞

dx(t

) exp(iS(

{

x(t

)

}

)) ,

varying over all possible positions x(t

) of the particle at this time step. The cor-

responding velocity can be determined from the trajectory of the particle. This

procedure can be used for every time step (see Fig. 7.2), yielding the transition

amplitude

x

)|x

)∼

N−1

;

n=1

dx(t

) exp(iS(

{

x(t

)

}

)) . (7.4)

Strictly speaking, one has to perform a careful limit for an inﬁnite number

(N →∞) of time slices and corresponding integrations in this formula for the

exact expression:

x

)|x

)=N lim

N→∞

N−1

;

n=1

dx(t

) exp(iS(

{

x(t

)

}

)) (7.5)

with a normalization factor N . As can be seen from (7.5), the discretization

of the time variable (a time lattice) is quite useful for formulating the idea of

summing over all paths in a practical manner. After studying the dynamics of

a single particle, i.e. one-body quantum mechanics, we can apply the same gen-

eral approach to ﬁelds. For simplicity we consider a real scalar ﬁeld Φ(x, t) in

one spatial dimension. The extension to higher dimensions is straightforward.

Again we study the transition amplitude for the ﬁeld having a value Φ

(x, t

) at

the beginning and Φ

(x, t

) at the end. The path integral method states that the

Fig. 7.2. Paths in space–

time between x

) and

) for discrete time

steps. Every possible path is

taken into account

444 7. Nonperturbative QCD

amplitude

Φ

(x, t

)|Φ

(x, t

)∼



exp



{

}

∂

%

(7.6)

is a weighted sum over all connecting paths P. We subdivide the time evolution

into N −1 steps as before using (7.3). In addition, as we consider space-

dependent ﬁelds, we will also discretize the space coordinates x into N

equally

spaced points x

,...,x

. Given this system of a ﬁnite number of points in

time and space directions as an approximation of the real continuous system, the

transition amplitude reads

Φ

(x, t

)|Φ

(x, t

)=N lim

→∞,N→∞

;

m=1

N−1

;

n=1

dΦ(x

, t

)

×exp



$

Φ(x

, t

), ∂

Φ(x

, t

)

%

. (7.7)

This is the formulation of the transition matrix element within the path inte-

gral formalism in quantum ﬁeld theory. Another typical feature of lattice gauge

calculations is that one prefers to calculate quantities in the imaginary time for-

malism (the reason for using imaginary time will become clearer in Sect. 7.1.8

on Monte Carlo methods). Formally this is done by replacing the real time t by

imaginary time τ using the equation t =−iτ. This corresponds to a Wick rota-

tion by π/2inthecomplext plane (see Sect. 4.3 for a Wick rotation in Fourier

space). In principle one can rotate results back to real time after ﬁnishing the cal-

culation. However, in practice this turns out to be rather difﬁcult. For the scalar

ﬁeld just discussed one introduces slices in the imaginary time coordinate τ.Take

the action of a scalar ﬁeld:

S =

dt d



∂

Φ∂

Φ −V(Φ)



(7.8)

with some potential or mass term summarized in V(Φ).Weget

S =−i

dτ d



(−∂

Φ∂

Φ −∇Φ∇Φ) −V(Φ)



. (7.9)

With τ ≡ x

the action can be written as

S = i



∂

Φ∂

Φ +V(Φ)



, (7.10)

where the summation over µ runs over µ = 1,...,4. Note that in this formula-

tion the metric tensor now is simply g

µν

≡ δ

µν

=diag(1, 1, 1, 1) so there is no

difference between subscripts and superscripts, i.e. space–time is Euclidean.

It is customary to remove the factor i in front of (7.10) from the deﬁnition of the action.

The Euclidean action S

is deﬁned as S

=−iS(t =−iτ).

7.1 Lattice QCD Calculations 445

The phase factor in the path integral formula (7.7) now reads

exp(iS) → exp(−S

). (7.11)

Thus for real and positive actions (or at least for actions bounded from below)

the phase factor has become a weighting factor so that one can adopt impor-

tance sampling techniques for the evaluation of the expression. This will be very

important for actual numerical calculations (see Sect. 7.1.8)

The Euclidean formulation allows a very direct connection of (7.7) with the

partition function Z of the theory of statistical mechanics. The partition function

is given by

Z =



Φ(x)|exp(−βH )|Φ(x) , (7.12)

summing over all possible states |Φ(x). β = 1/(kT ) is the inverse temperature

of the system. We rewrite this expression as

Z =



exp(−Hβ)Φ(x)|Φ(x)



Φ(x, t =−iβ)|Φ(x, t = 0) , (7.13)

which corresponds to the transition amplitude (7.7). The difference is that now

the initial and ﬁnal states Φ

, Φ

are the same in (7.12) and the variables over

which the sum is performed, which can be incorporated by imposing periodic

boundary conditions on Φ in time direction with a period τ = β. Thus we have

Z = N

lim

→∞,N→∞

;

n=1

;

m=1

dΦ(x

,τ

) exp(−S

({x

)}))

= N

[

dΦ

]

exp(−S

). (7.14)

The bracketed term [dΦ] is a short-hand notation for the product of the whole

integration measure. We will see later that the normalization factor N drops out

when observables are calculated.

EXERCISE

7.1 Derivation of the Transition Amplitude (7.5)

Problem. Derive the transition amplitude (7.5) from the concept of path inte-

grals.

Solution. We extract the time dependence of the state vectors

T ≡x

)|x(t

)=x

|exp



−i

H(t

−t

)



|x . (1)

446 7. Nonperturbative QCD

Exercise 7.1

In the next step we divide the time interval (t

−t

) into N −1 intermediate time

steps with ∆t = (t

−t

)/N as done before in (7.3):

T =x

≡ x

|exp



−i

H∆t



exp



−i

H∆t



···

89 :

N times

≡ x

 (2)

and insert complete sets of eigenstates of the positions between each step

T =x

|exp



−i

H∆t



N−1

x

N−1

|exp



−i

H∆t



N−2

x

N−2

|···exp



−i

H∆t



 . (3)

In addition we also insert complete sets of momentum eigenstates into (3)

T =

···dx

N−1

2π

···

N−1

2π

×x

N−1

p

N−1

|exp(−i

H∆t)|x

N−1



×x

N−1

N−2

p

N−2

|exp(−i

H∆t)|x

N−2



×···×p

 . (4)

The main purpose of the whole procedure is that for sufﬁciently large N and

small ∆t one can expand the exponential

exp(−i

H∆t) ∼ 1 −i∆t

H . (5)

In (4) the operator

H is sandwiched between eigenstates of the position and

momentum operator. Thus, using

x|x=x|x and

p|p=p|p we can replace

the operators in

H by their eigenvalues:

p|

x)|x=p|H(p, x)|x=

p|xH(p, x). This is the main trick used in the path integral formalism: op-

erators are replaced by c numbers at the cost of (inﬁnitely) many sets of basis

states representing the possible paths of the particle. Using this results and

x|p=exp(i px) we obtain the expression

T =

N−1

;

n=1

N−1

;

m=0

2π

exp



N−1



n=0

n+1

−x

)



N−1

;

n=0

(1 −i∆tH( p

, x

))

N→∞

[

][

]

exp(i



t( p

x −H(p, x))) . (6)

Some care has to be taken with the ordering of the operators when the Hamiltonian

contains mixed products of position and momentum operators.

7.1 Lattice QCD Calculations 447

Equation (6) is the path integral in phase space. Depending on the speciﬁc struc-

ture of H it is rather straightforward to get rid of the momentum integration if H

is quadratic in the momentum, e.g.

H =

+U(x). (7)

Using this expression we see that we can complete the square with respect to the

momentum variable in (6):

T = N

[

][

]

exp

⎛

⎜

⎝

−i



( p −m

−

+U(x)



⎞

⎟

⎠

(8)

Now one can transform the variable p



= p −m

x, which amounts to a Legendre

transformation, and integrate the Gaussian integral of p



, which generates

a constant that can be absorbed in the normalization factor:



[

]

exp

⎛

⎜

⎝





−U(x)



⎞

⎟

⎠



[

]

exp(iS). (9)

Equation (9) is the path integral formula in the Lagrange formalism (7.5), here

in Minkowski space–time.

7.1.2 Expectation Values

One can calculate expectation values of operators in the path integral method

in a very straightforward way. One important observable in quantum mechan-

ics and ﬁeld theory is the two-point correlation function or propagator, deﬁned

G(t

, t

) =0|T(

q(t

)

q(t

))|0 (7.15)

in the case of a one-body quantum-mechanical system. Considering the

quantum-mechanical case it describes the correlation of the position of a particle

at different times t

, t

,where|0 is the ground state of the system. The time

Exercise 7.1

448 7. Nonperturbative QCD

evolution of a general state is

|q(t)=exp(−iHt)|q(0)

= exp(−iHt)



|nn|q(0)



exp(−iE

t)|nn|q(0) , (7.16)

where a complete set of energy eigenstates with H|n=E

|nhas been inserted.

Let us now consider the path integral with t < t

, t



> t

, t

,andt

> t

.Using

(7.16) we get

q(t



q(t

)

q(t

)|q(t)=



n,m

exp(+i(E

t −E



))

∗

(q)



)

×n



q(t

)

q(t

)|n (7.17)

with 

(q) ≡q|n. We switch to imaginary time τ = it as discussed before:

q(τ



q(τ

)

q(τ

)|q(τ)=



n,m

exp(+E

(τ −τ

) −E



(τ



−τ

))

×

∗

(q)



)n



q(τ

)

q(τ

)|n . (7.18)

With τ →−∞and τ



→+∞the sum is dominated by the groundstate contri-

bution n = m = 0

q(+∞)|

q(τ

)

q(τ

)|q(−∞)=exp(+E

(τ −τ



))

(q)



)

×0|

q(τ

)

q(τ

)|0 . (7.19)

By considering the ratio

q



(τ



q(τ

)

q(τ

)|q(τ)

q



(τ



)|q(τ)

(7.20)

and using (7.19) for the nominator and denominator we get

q



(τ



q(τ

)

q(τ

)|q(τ)

q



(τ



)|q(τ)

=0|

q(τ

)

q(τ

)|0 (τ →−∞,τ



→∞).

(7.21)

The path integral (7.4) is just the transition amplitude between different states,

i.e. the denominator of expression (7.21). Following the earlier argument one

can again split the time interval into many intermediate steps and replace the

operators

q(t

) by their eigenvalues.

Note that by inserting a sequence of intermediate states one automatically

generates the time-ordered product T(

q(t

)

q(t

)). Altogether we have (in real

time)

0|T



q(t

)

q(t

)



|0=

[

]

q(t

)q(t

) exp(iS(q,

q))

[

]

exp(iS(q,

q))

. (7.22)

7.1 Lattice QCD Calculations 449

In the same way as for the extension of the path integral from quantum mechan-

ics to quantum ﬁeld theory, (7.22) can be used in a ﬁeld-theoretical context, too.

For general operators

O containing s ﬁeld operators

Φ one obtains the vacuum

expectation value

0|





|0=

[

dΦ

]

O(Φ) exp(iS({Φ}, {∂

Φ}))

[

dΦ

]

exp(iS({Φ}, {∂

Φ}))

, (7.23)

where O(Φ) is the c-number expression with respect to the ﬁelds Φ corre-

sponding to the operator

O. Equation (7.23) is the basic formula for calculating

observables on the lattice. The straightforward possibility of discretization of the

expression and the fact that there are no operators in the path integral formalism

renders this approach very suitable for numerical calculations. However, ﬁrst the

theory of QCD has to be formulated on a lattice, which will be discussed in the

following section.

7.1.3 QCD on the Lattice

The basic idea of a lattice calculation is to reduce the inﬁnite number (more

precisely, the continuum) of ﬁeld variables to a ﬁnite tractable number by

discretizing space and time. In the following we (and most of the current state-

of-the-art calculations) will adopt the most simple discretization. We introduce

a hypercubic equally spaced lattice in space and time with coordinates (time

being the 4th coordinate x

)

→ x(i, j, k, t) = (ie

+ je

+ke

+te

)a , (7.24)

where a is the lattice spacing, the distance between neighboring lattice points. In

the next step we have to formulate the QCD gauge theory on this lattice struc-

ture, i.e. ﬁnd a discretized version of (4.57). The guideline for describing a gauge

theory on the lattice is the implementation of the gauge principle on the lat-

tice structure. The Lagrangian should be gauge invariant, that is, invariant with

respect to arbitrary local phase rotations of the ﬁelds in color space. This was

also one of the essential requirements (the conceptual basis of a gauge theory)

in the case of continuous space–time. In Example 4.1 we discussed the geomet-

ric properties of a gauge theory and introduced the notion of parallel transport.

This is exactly what is needed in this context. One has to construct a method to

transfer the value of the gauge ﬁeld at one point of the lattice to another. To do

this we have to generalize the parallel transport by an inﬁnitesimal amount in

space–time dx

to a ﬁnite step from one lattice point to a neighboring one. The

inﬁnitesimally shifted quark ﬁeld Ψ(x) reads ((8) in Example 4.1)

Ψ(x + dx) = (

11 + dx

)Ψ(x), (7.25)

where D

is the usual covariant derivative D

=11 ∂

−i

(x). Here and in the

rest of the chapter we will use the matrix notation of the gluon ﬁelds following

(4.49), i.e.

(x) ≡



(x). In contrast to the case of (4.54) we also absorb