Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

6.1 The Drell–Yan Process 429

full propagator we retain only its imaginary part:

p/ +q/

i(x

p/ +q/)

p +q)

+i"

→(x

p/ +q/)(2π)δ

((x

p +q)

). (10)

The general rules for obtaining from a Feynman amplitude the discontinu-

ity across a cut were ﬁrst obtained by Cutkosky.

As soon as more than one

propagator has to be cut the rules are not as straightforward as in our case. The

one-dimensional δ function becomes

(2π)δ((x

p +q)

) =



2π)δ(−Q

+2x

2xp



=(2π)δ



−x)



=(2π)

δ(x

−x), (11)

so that (9) simpliﬁes to

µν



(xp/ +q/)γ



−

2π

ix( p

−

)



q(0)n/q(x

−

)







(xp/ +q/)γ

p/γ



−

2π

ix( p

−

)



q(0)γ

n/q(x

−

)





+(q ↔−q;µ ↔ ν) . (12)

To complete our task we calculate the traces. For the trace without γ

obtain



(xp/ +q/)γ



·2



2xp

−g

µν

p ·q +O(q

, q

)



=2x

p ·q

−g

µν

+O(q

, q

). (13)

Note that we have neglected all terms that lead to zero after contracting with the

leptonic tensor. Comparing with the parametrization of the hadronic tensor we

can identify

(x) =

−

2π

+ix( p

−

)





(0)n/q

−

)





(x) = 2xF

(x). (14)

Note that we have taken into account the exchange term (q ↔−q;µ ↔ ν) and

made explicit the dependence on the quark ﬂavor. In a similar way we ﬁnd for

R.E. Cutkosky, J. Math. Phys. 1, 1344 (1958). See also C. Itzykson and J.-B. Zuber:

Quantum Field Theory (McGraw-Hill, New York, 1978).

Exercise 6.6

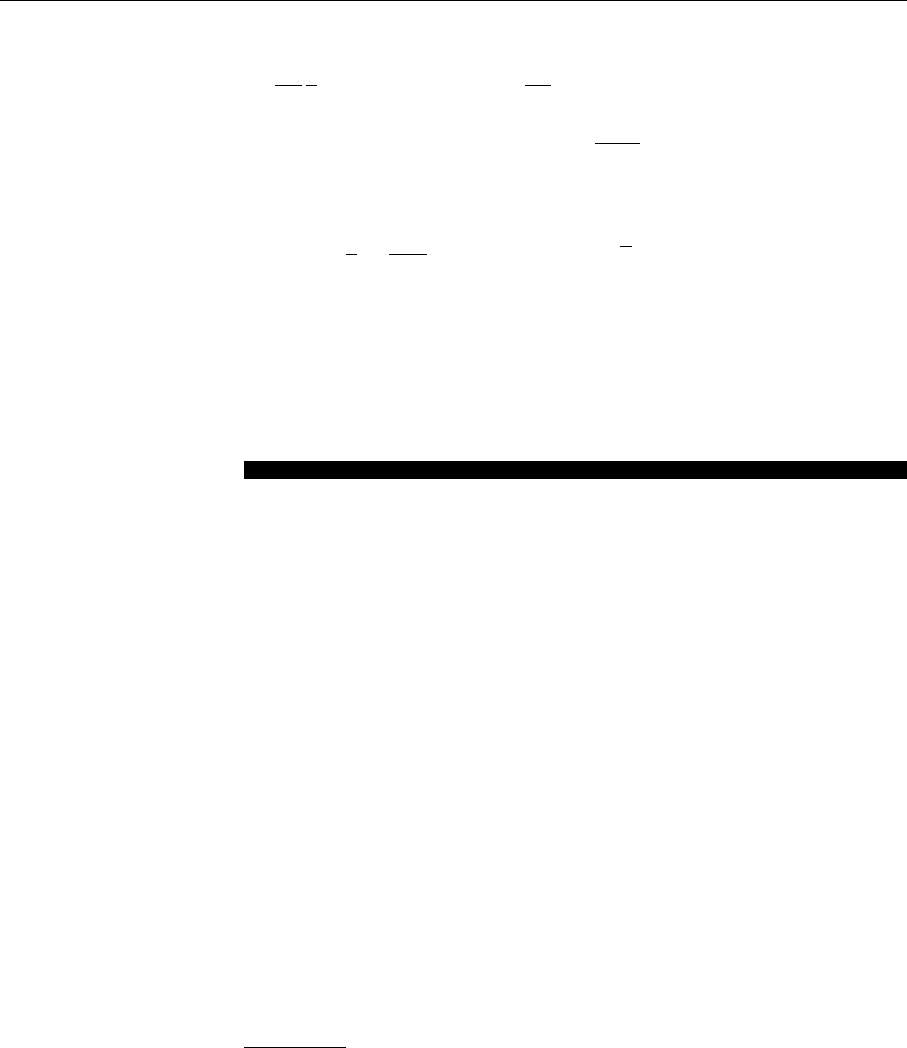
430 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics

Exercise 6.6

the spin dependent function



(xp/ +q/)γ

p/γ



ναµβ

=−i"

µνλσ

p ·q

. (15)

For longitudinal polarization p

∼ S

we can identify in a similar way

(x) =

−

2π

+ix( p

−

)





(0)γ

n/q

−

)





. (16)

Hence we have proven that the hadronic tensor can be parametrized in terms of

bilocal twist-2 operators along the light cone. In our analysis we conﬁrmed once

more the validity of the Callan–Gross relation

(x) =+2xF

(x). (17)

6.2 Small-x Physics

In the previous sections we acquainted ourselves with the leading-log approx-

imation, which enables us to resum all terms which contain factors log(t) and

t = Q

/µ

and are of lowest order in α

. We now turn, however, to a kinematical

range in which the leading-log approximation (LLA) is not sufﬁcient, namely to

deep inelastic scattering at very small x, more precisely, for x so small that e.g.

(α

/π) log

(

1/x

)

> 1. With the completion of the HERA accelerator at DESY

this region (down to x ∼ 10

−5

) became accessible for the ﬁrst time, generating

an intense theoretical effort to isolate, understand, and resum the relevant graphs.

In these reactions Q

is still rather large, so that perturbation theory should be

applicable.

However, the small-x physics is a very complicated subject with a variety

of theoretical approaches. In the literature there exist comprehensive theoretical

reviews addressing the advanced reader.

We will restrict ourselves to an overview of existing theoretical approaches

and refer the reader to the more detailed original literature. In our overview

we follow the presentation by Badelek et al.

We shall start by discussing the

L.V. Gribov, E.M. Levin, M.G. Ryskin: Phys. Rept. 100, 1 (1983),

E.M. Levin, M.G. Ryskin: Phys. Rep. 189, 267 (1990).

B. Badelek, M. Krawczyk, K. Charchula, J. Kwiecinski, DESY 91-124: Rev. Mod.

Phys. 64, 927 (1992).

6.2 Small-x Physics 431

Fig. 6.17. Virtual Compton

scattering of a photon with

momentum q on a nucleon

target

elements of Regge theory and its consequences for deep inelastic scattering on

a nucleon. Let us consider once more the DIS process

lN→l



X , (6.75)

where lepton l scatters off nucleon N and produces the ﬁnal hadronic state X.



denotes the scattered lepton. The interaction is mediated by the exchange of

a vector boson, γ or Z

for the neutral current, W

for charged current inter-

actions. At ﬁxed energy the kinematics of inelastic lepton–nucleon scattering is

determined by two independent variables. As usual we can choose the Bjorken

parameter x = Q

/2p ·q and Q

=−q

, the “mass” of the exchanged boson.

q is the four-momentum transfer between the leptons, p the momentum of the

proton. As will become apparent, small-x behavior of structure functions for

ﬁxed Q

reﬂects the high-energy behavior of the virtual Compton scattering

amplitude.

Recall that the Bjorken limit is deﬁned as the limit where Q

and ν = p ·q

both go to inﬁnty while their ratio Q

/2p ·q = x stays ﬁxed.

The total center-of-mass energy in the process depicted in Fig. 6.17 is

s = ( p +q)

≈2pq −Q

(1 −x), (6.76)

expressedintermsofx and Q

. The limit s →∞corresponds therefore to the

limit where x → 0,

s  Q

↔ x  1 . (6.77)

The small-x limit of deep inelastic scattering is therefore the limit where the

scattering energy is kept much larger than all external masses and momentum

tranfers. This is by deﬁnition the Regge limit. In deep inelastic scattering Q

deﬁnition is kept large, the limit where in addition s is large also, is the Regge

limit of deep inelastic scattering. The old concepts of Regge theory and Regge

phenomenology acquire a new content within the modern concept of QCD. It

may be helpful to recapitulate some elements of Regge theory.

See, for example, P.D.B. Collins: An Introduction to Regge Theory and High-Energy

Physics (Cambridge University Press, Cambridge 1977).

432 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics

pppp

pnn

R=r

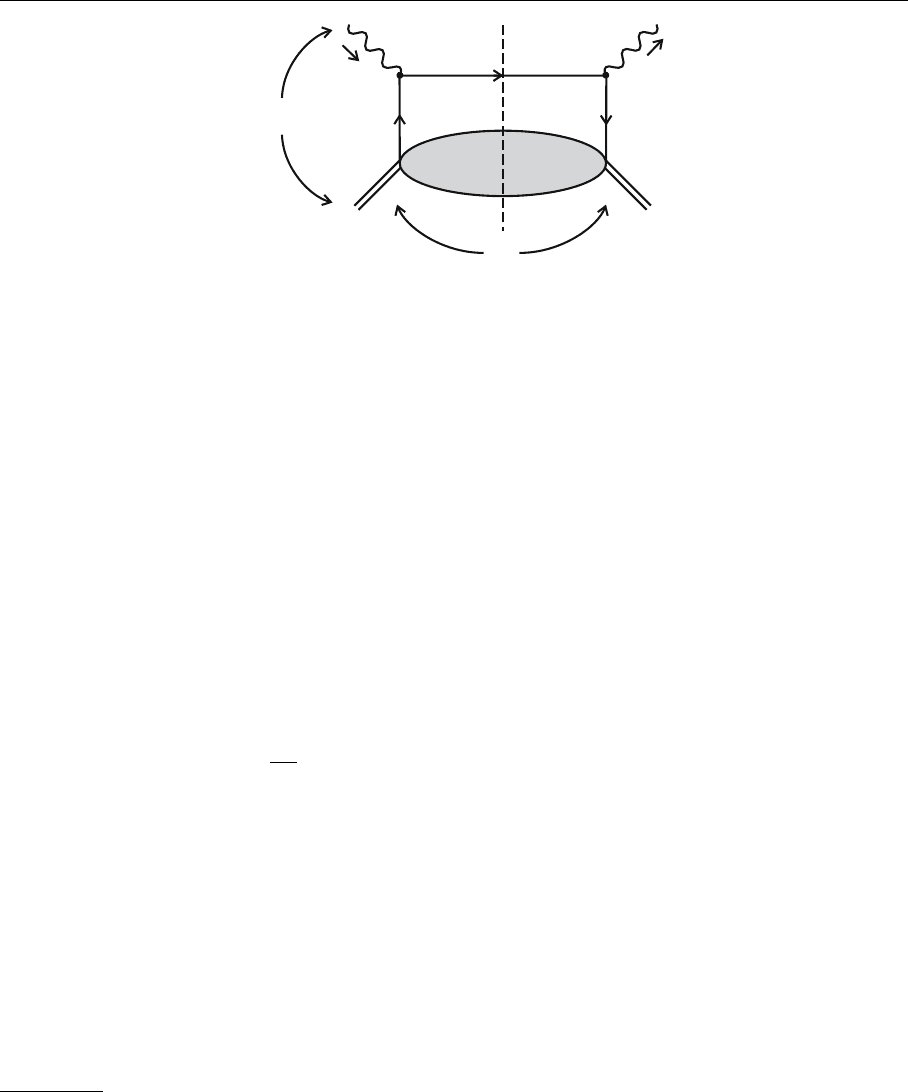
Fig. 6.18. Exchange of a q

pair viewed as reggeon ex-

change: π

−

p →π

n scat-

tering at high energies can

be parametrized as  ex-

change. Exchange of a gluon

pair corresponds to pomeron

exchange in high energy

p →π

It is known that two-body scattering of hadrons is strongly dominated by

small squared momentum transfer t or equivalently by small scattering angles.

This behavior is modeled by assuming the exchange of particles with appropri-

ate quantum numbers. Regge exchange is a generalization of this concept. In this

description Regge poles rather than particles are exchanged. The Regge poles are

characterized by quantum numbers like charge, isospin, C parity, parity, etc.

Especially the Regge pole that carries the quantum numbers of the vacuum

) is called the pomeron. Pomeron exchange dominates, for instance,

the total cross section of proton–proton and proton–antiproton scattering.

Other Regge poles are called reggeons. For example, -meson exchange can

be considered as reggeon exchange. Instead of talking about  exchange in terms

of meson exchange it is useful to consider this at the level of quarks and gluons.

Thus the exchange of q

q pairs that carry quantum numbers different from those

of the vacuum can be classiﬁed by reggeons; exchange of gluons with quantum

numbers of the vacuum can be considered as pomeron exchange (see Fig. 6.18).

Regge pole exchange describes the exchange of states with appropriate quan-

tum numbers and different virtuality t and spin α. The relation between t and α is

called the Regge trajectory, α(t). Whenever this function passes through an inte-

ger (for bosonic Regge poles) or half-integer (for fermionic Regge poles), i.e.

α(t) = n, n = 1, 2, ··· or n =

, ···, there should exist a particle of spin n

and mass M

√

t. The trajectory α(t) thus interpolates between particles of

different spins.

It can be shown that the exchange of states as described above leads to a pole

in the scattering amplitude, or more precisely a pole in the partial wave ampli-

tude. The trajectory α(t) describes the t dependence of the pole of the partial

wave amplitude in the complex angular momentum plane.

6.2 Small-x Physics 433

At high energies the asymptotic behavior of a two-body amplitude can be

parametrized as

A(s, t) ∼ s

α(t)

. (6.78)

The optical theorem relates the imaginary part of the forward scattering

amplitude to the total cross section:

ImA(s, t = 0) = sσ

tot

. (6.79)

Regge theory therefore predicts that the total cross section behaves as

tot

α(0)−1

, (6.80)

where α(t = 0) = α(0) is called the intercept.

Non-vacuum trajectories of Regge poles associated with the known meson

have intercepts smaller than one (α

≈

or less). Thus the total cross section

decreases with increasing energy. However, in p

p and pp scattering an increase

in the total cross section with energy has been observed and no known reggeon

can be attributed to this behavior. High-energy p

p and pp scattering is therefore

associated with the pomeron, which is assumed to have an intercept close to one,

(0) ≈ 1. It should be emphasized that the particular nature of the pomeron

is not yet completely understood. The name pomeron is in general a name for

the mechanism that leads to an increase in the cross section with increasing en-

ergy. Note, however, that the increase in the cross section is assymptotically

constrained by the Froissart bound;

i.e. based on unitarity and analyticity of the

amplitude it can be shown that the total cross section cannot increase faster than

log

It should be stressed that this bound is an asymptotic one: for ﬁnite energies

the total cross section can still behave like

> 1,σ

tot

∼s

−1

How can Regge theory be applied to deep inelastic lepton nucleon scattering?

The natural quantities to consider are the structure functions F

and F

,which

are proportional to the total virtual photon nucleon cross section γ

∗

N → X. This

cross section is expected to show Regge behavior for s →∞.

We have shown above (see (6.76)) that the high-energy limit s →∞corres-

ponds to x → 0, s ∼

. In the parton model the structure functions are related

to quark antiquark distributions in the nucleon. The Regge behavior of the cross

section is reﬂected in the small-x behavior of the structure function. Due to the

quantum numbers of the operators that determine the distribution function, the

sea quark distribution and the gluon distribution is expected to reﬂect the Regge

behavior of the pomeron:

sea

(x, Q

) ∼ x

1−α

xG(x, Q

) ∼ x

1−α

. (6.81)

M. Froissart: Phys. Rev. 123, 1053 (1961).

434 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics

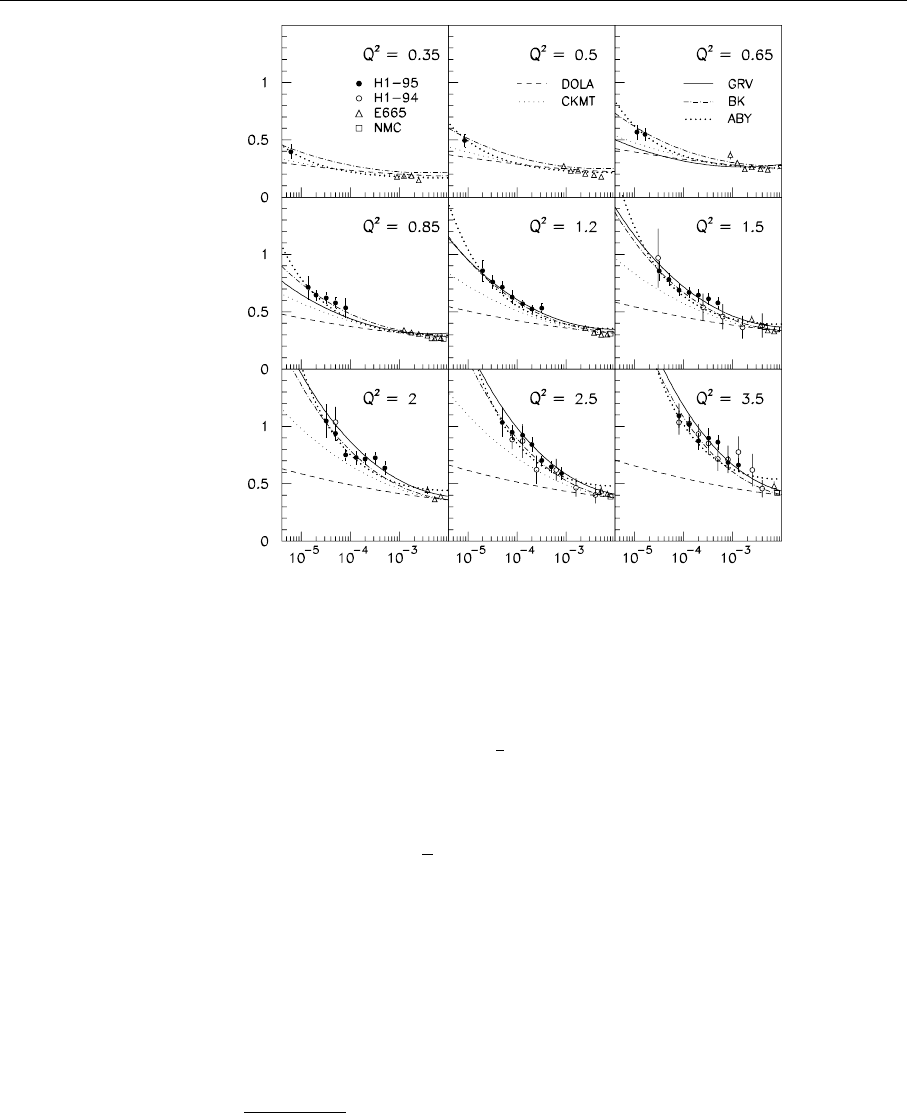
Fig. 6.19. Measurement of

the proton structure function

(x, Q

) in the low-Q

re-

gion by H1 (full points), to-

gether with previously pub-

lished results from H1 (open

circles), E665 (open trian-

gles), NMC (open squares).

The Q

values are given

in GeV

. Various predic-

tions for F

are compared

with the data: the model of

Donnachie and Landshoff

(dashed line), the model

of Capella et al. (dotted

line/small), the model of

Badelek, and Kwiecinski

(dashed–dotted line), the

model of Glück, Reya, and

Vogt (full line) and the

model of Adel et al. (dotted

line/large). Global normal-

ization uncertainties are not

included

On the other hand, the behavior of the valence quarks follows the Regge

exchange of mesonic poles:

val

(x, Q

) ∼ x

1−α

. (6.82)

Assuming α

∼ 1,α

∼

we obtain the Regge prediction:

sea

(x, Q

) ∼ x

xG(x, Q

) ∼ x

val

(x, Q

) ∼

√

x . (6.83)

A detailed analysis of small-x structure function measurements shows that

they are indeed consistent with predictions of Regge theory. For example, the

behavior xG (x, Q

) ∼ x

, xq

sea

(x, Q

) ∼ x

at small x can be observed in

Fig. 6.19.

But a modiﬁcation of this behavior is still seen from Fig. 6.19 if Q

increases.

The steepening of the behavior at small x as Q

increases may be attributed to the

perturbative evolution of the structure functions discussed in previous chapters.

Indeed HERA data are well described by NLO GLAP-based ﬁts. The analysis

H1 collaboration (C. Adloff et al.): Nucl. Phys. B 497, 3 (1997).

6.2 Small-x Physics 435

shows that the ∼ x

behavior of the sea quark and gluon distributions is unstable

for Q

> Q

. The evolution equations generate steeper behavior.

In Chap. 5 we have discussed these evolution equations. In the leading-log

approximation, which keeps only the leading power of ln(Q

),i.e.α

we get the well-known GLAP equations. When a physical gauge is chosen, this

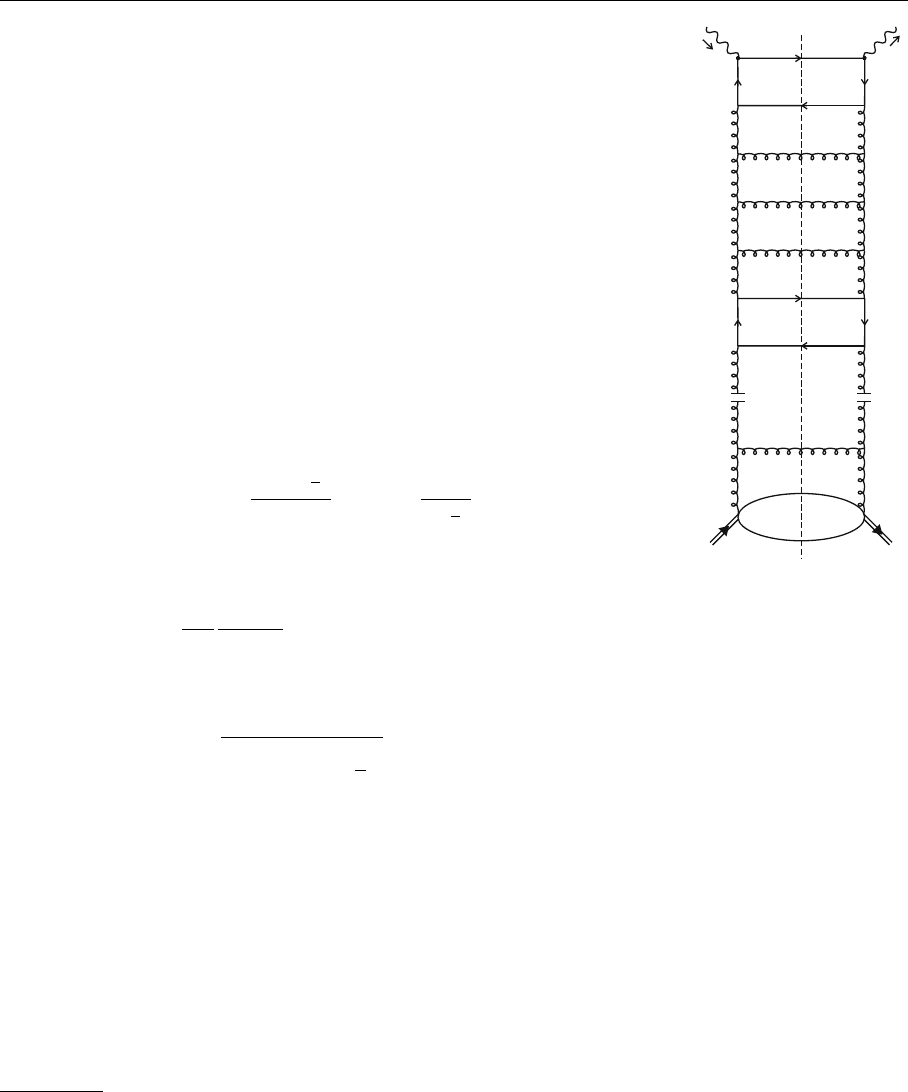
approximation corresponds to resumming ladder diagrams with gluon and quark

exchange (see Fig. 6.20). When terms with higher powers of the coupling α

)

are included, one obtains the next-to-leading-logarithmic approximation. Instead

of the next-to-leading-log approximation we are concerned with the small-x

limit of the GLAP evolution. To this end we note that the gluon splitting function

(z) behaves as 6/z at small z (see, e.g., (5.72)), which is relevant at small x.

(Remember that P

(z) enters as P

(x/y) in the evolution equations.)

Retaining only these terms in the GLAP equations, one gets maximal powers

of both large logarithms ln(Q

) and ln

(

1/x

)

. This approximation is called the

double logarithmic approximation. The powers of ln

(

1/x

)

come from the fact

that the integrations over the longitudinal momentum fraction become also loga-

rithmic, and, therfore, in the nth order given by the nth iteration of the evolution

equations one ﬁnds

G(x, Q

) ∼ η



, Q



n−1





x(n!)



1 +O









, (6.84)

where



, Q



3α

)

. (6.85)

The iterations can be summed to give

xG(x, Q

) ∼ exp





, Q









(6.86)

at small x and large Q

The gluon and sea quark distributions are therefore found to grow faster than

any power of ln

(

1/x

)

in the small-x limit. Note that the dominant contribution

to the sea quarks comes from q

q pairs emitted from gluons.

Sometimes it is convenient to discuss the behavior of the structure functions

in terms of moments instead of the functions itself. Introducing

) =

dxx

n−1

G(x, Q

), (6.87)

R.K. Ellis, W.J. Stirling, B.R. Webber: QCD and Collider Physics (Cambridge

University Press, 1996).

Fig. 6.20. The ladder dia-

gram that contributes to DIS

in leading-log approxima-

tion

436 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics

the evolution equations can be solved in closed form (see similar discussion for

(5.194)) to give

) =

) exp



(n)η



, Q



(6.88)

where

(n) =

dzz

n−1

(z) (6.89)

is the moment of the splitting function and

) corresponds to the starting

contribution of Q

. If we keep only the most singular term in P

then d

(n)

becomes

(n) ≈

(n −1)

. (6.90)

From (6.90) it follows that the moment

) has an essential singularity at

n = 1. This is the leading singularity and it generates the small-x behavior given

by (6.86).

The solution of the evolution equations for the moments q

val

) of the

valence quark distribution is accordingly

val

) =

val

) exp



(n)η



, Q



(6.91)

with

(n) =

dzz

n−1

(6.92)

and the leading pole of the anomalous dimensions in d

(n) is at n = 0(seeEx-

ample 5.8). The moment of the starting distribution will have a pole at n = 1/2

due to the general Regge arguments given above. Thus this pole will remain

the leading singularity of the moment q

val

) and the small-x behavior of

the valence quark distribution will consequently remain unchanged by QCD

evolution.

Attempts have been made to go beyond the double logarithmic approxima-

tion. To explain this it should be noted that the leading logs can be traced to

those contributions in the diagram (Fig. 6.20) where the momenta are strongly

ordered. In those diagrams the longitudinal momenta ∼ x

are ordered along

the chain (x

≥ x

i+1

) and the transverse momenta are strongly ordered as well,

(i.e. k

⊥i

k

⊥i+1

). It is the strong ordering of transverse momenta towards Q

which gives the maximal power of ln(Q

), since the integration over transverse

momentum in each cell is logarithmic.

Going beyond the double logarithmic approximation means summing those

terms which contain the leading ln

(

1/x

)

and retain the full Q

dependence.

6.2 Small-x Physics 437

This approximation leads to the Balitsky–Fadin–Kuraev–Lipatov (BFKL) equa-

tion.

In general the summation of ln

(

1/x

)

terms is refered to as the leading

(

1/x

)

approximation. This approximation gives the bare pomeron in QCD.

The diagrams are the same as mentioned above, yet the transverse momenta of

the gluons are no longer ordered. The equation that sums these diagrams is

f(x, k

) = f 0(x, k

) +

3α

)



∞



)

f(x



, k



) − f(x



, k

)



−k

f(x



, k

)



(6.93)

where the function f(x, k

) is the nonintegrated gluon distribution, i.e.

f(x, k

) =

∂xG(x, k

)

∂ ln(k

)

, (6.94)

where k

, k



are the transverse momenta squared of the gluon in the initial and

ﬁnal states respectively; k

is a cutoff.

When effects of the running coupling are neglected, i.e. if a ﬁxed coup-

ling α

) = α

is used, the BFKL equation can be solved analytically. And at

small x one obtains

xG(x, Q

) ∼

1−α

[

ln(x)

]



1 +O



ln(x)



(6.95)

with

= 1 +

12α

ln(2) = 1 +ω

, (6.96)

which corresponds to the intercept of the bare QCD pomeron. It should be no-

ticed that this leads to a large number α

for typical values of α

.Takingthe

running of the coupling into account this picture does not change very much. Still

the pomeron intercept is quite large, α

∼

. This is in contrast to the nonper-

turbative “soft” pomeron, which is used to ﬁt data in high-energy pp collisions.

This intercept is 1.08.

Note that (6.95) and (6.96) suggest that the gluon distribution (multiplied

by x), i.e. the function xG(x, Q

), can grow arbitrarily in the small-x limit. Quite

obviously such behavior is forbidden by the ﬁnite size of the nucleon.

At a certain stage the gluons can no longer be treated as free particles. They

begin to interact with each other. This interaction leads to screening and shad-

owing effects so that an inﬁnite increase in the number density is tamed. These

See e.g. L. Lipatov, in Perturbative QCD, ed. by A.H. Mueller (World Scientiﬁc,

Singapore 1989), p. 411 and references therein.

A. Donnachie and P.V. Landshoff: Nucl. Phys. B 231, 189 (1984).

438 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics

Fig. 6.21. Graphical repre-

sentation of the quadratic

shadowing term in the evo-

lution equation (6.97). The

box represents all possible

pertubative QCD diagrams

which couple four gluons to

two gluons. The lower blob

represents the nucleon

shadowing effects modify the evolution equations as well as the BFKL equa-

tion by nonlinear terms. Including shadowing corrections, the BFKL equation

assumes the following form

−x

∂ f(x, k

)

∂x

3α

)

∞



⎧

⎨

⎩

f(x, k



) − f(x, k

)



−k

f(x, k

)







⎫

⎬

⎭

−

)



xG(x, k

)



. (6.97)

This equation is called the Gribov–Levin–Ryskin (GLR) equation.

The sec-

ond term on the right-hand side describes the shadowing effects. Note that this

term is quadratic in the gluon distributions. The parameter R describes the size

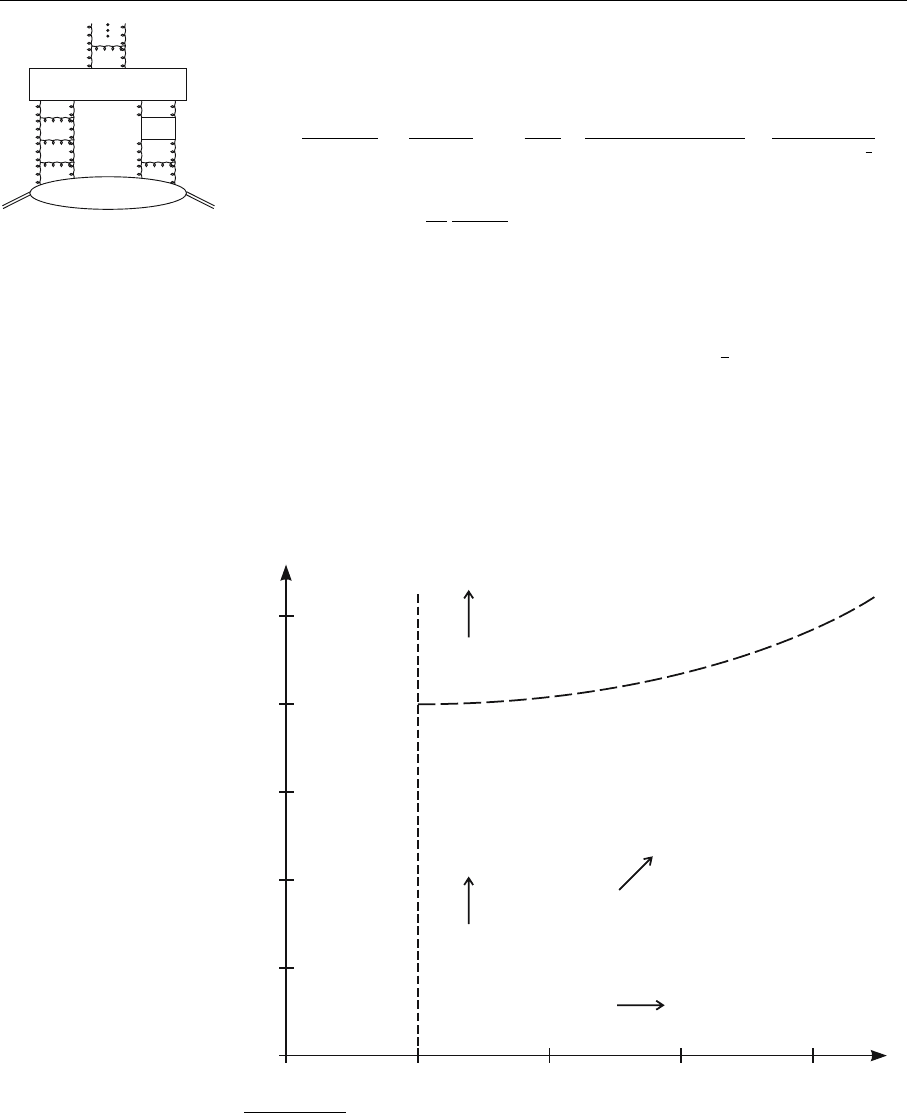
of the region within which the gluons are concentrated (see Fig. 6.21). In Fig-

ure 6.22 we have summarized the various regions in the

, Q

plane where the

different equations and phenomenological descriptions might be applicable and

in which direction the evolution manifests itself.

The complete discussion of BFKL and GLR equations would be far too

lengthy, and, furthermore, the validity of these equations is presently very much

under discussion. In particular, doubt was cast on the validity of the BFKL

equation since NLO corrections were calculated which turned out to be larger

0,1

10 100

1000

1/x

Regge Phenomenolegy

BFKL

GLR

GLAP

DLLA

Screening region

Fig. 6.22. The various evo-

lution equations depicted in

the (1/x, Q

) plane as dis-

cussed in the text

L.V. Gribov, E.M. Levin, M.G. Ryskin: Phys. Rep. 100, 1 (1983).