Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


6.1 The Drell–Yan Process 419
This completes our calculation:
dΓ =
M
64π
3
dx
1
dx
2
S
11
+S
12
+S
22
=
M
64π
3
dx
1
dx
2
16πα
s
4πα e
2
q
×
8
1 −2x
1
1 −2x
2
+8
1 +4x
2
2
(1 −2x
2
)(1 −2x
1
)
−16
1
1 −2x
2
=
8M
π
α
s
αe
2
q
dx
1
dx
2
−(1+2x
1
)(1 −2x
1
) +1 +4x
2
2
(1 −2x
2
)(1 −2x
1
)
= 3αe
2
q
M
32
3π
α
s
x
2
1
+x
2
2
(1 −2x
2
)(1 −2x
1
)
dx
1
dx
2
. (28)
EXAMPLE
6.5 Factorization in Drell–Yan
In this example, we derive the cross section for the Drell–Yan process
N + N → µ
+
µ
−
+X (1)
in the most general form (Fig. 6.15). N represents the nucleon, µ
+
and µ
−
the
charged leptons and X the unobserved hadrons. In (6.6) we assumed that the
cross section can be written as a convolution of the elementary parton–parton
cross section and the structure functions known from deep inelastic lepton–
nucleon scattering. In the following it will be shown that such a factorization can
actually be derived from QCD.
The cross section in general can be written as
dσ =
1
2(p
1
· p
2
)
1
4
pol
d
3
k
1
(2π)
3
2k
0
1
d
3
k
2
(2π)
3
2k
0
2
×
X
(2π)
4
δ
4
( p
1
+ p
2
−k
1
−k
2
− p
X
)
,
µ
+
µ
−
X
T
|
NN
2
, (2)
where p
1
and p
2
are the momenta of the nucleons, k
1
, k
2
the momenta of
the produced leptons, and the center-of-mass energy s =( p
1
+ p
2
)
2
=2p
1
· p
2
.
We neglect the masses of the leptons and nucleons. The sum runs over all po-
larizations of initial nucleons and final leptons. The factor 1/4 stands for the
average over the initial polarizations. The matrix element in the one-photon
approximation can be written as
,
µ
+
µ
−
X
T
|
NN
= u(k
1
)eγ
µ
v(k
2
)
g
µν
(k
1
+k
2
)
2
X
|
ej
ν
(0)
|
NN
(3)
Exercise 6.4
q
X
N(p )
1
N(p )
2
m
-
(k )
1
m
+
(k )
2
Fig. 6.15. Drell–Yan µ
+
µ
−
pair production in nucleon–
nucleon collisions

420 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
Example 6.5
with j
ν
(0) the electromagnetic current (we neglect Z and W exchange). Squaring
the matrix element and performing the sum over lepton polarizations we arrive
at
1
4
pol
,
µ
+
µ
−
T
|
NN
2
=
e
4
Q
4
1
4
tr
γ
µ
k/
2
γ
ν
k/
1
×
X
NN
|
j
ν
(0)
|
X
,
X
j
µ
(0)
NN
(4)
with the timelike momentum q = (k
1
+k
2
), q
2
= Q
2
. The sum over final
hadrons can be performed by making use of the δ function in (2):
(2π)
4
δ
4
( p
1
+ p
2
− P
X
−q)
,
X
j
µ
(0)
NN
=
d
4
x e
−i( p
1
+p
2
−P
X
−q)·x
,
X
j
µ
(0)
NN
=
d
4
x e
iqx
e
iP
X
·x
,
X
j
µ
(0)
NN
e
−i( p
1
+p
2
)·x
=
d
4
x e
iq·x
-
X
e
i
ˆ
P·x
j
µ
(0)e
−i
ˆ
P·x
NN
.
=
d
4
x e
iq·x
,
X
j
µ
(x)
NN
. (5)
Insertion into (2) finally leads to
dσ =
1
2s
e
4
Q
4
1
4
tr
γ
µ
k/
2
γ
ν
k/
1
×
d
4
x e
iqx
,
NN
j
ν
(0) j
µ
(x)
NN
d
3
k
1
(2π)
3
2k
0
1
d
3
k
2
(2π)
3
2k
0
2
,
where a complete set of states has been summed:
X
NN
|
j
ν
(0)
|
X
,
X
j
µ
(x)
NN
=
,
NN
j
ν
(0) j
µ
(x)
NN
. (6)
Defining the leptonic tensor as
1
4
tr
γ
µ
k/
2
γ
ν
k/
1
=
1
2
L
µν
(7)
and the hadronic tensor as
W
µν
=
d
4
x e
iq·x
,
NN
j
ν
(0) j
µ
(x)
NN
, (8)
we get as a result
dσ =
1
2s
e
4
Q
4
L
µν
2
W
µν
d
3
k
1
(2π)
3
2k
0
1
d
3
k
2
(2π)
3
2k
0
2
=
α
2
2s
1
Q
4
2L
µν
W
µν
1
(2π)
4
d
3
k
1
2k
0
1
d
3
k
2
2k
0
2
(9)
with α =e
2
/4π the electromagnetic fine-structure constant.

6.1 The Drell–Yan Process 421
The expression can be further simplified by introducing coordinates
q = k
1
+k
2
and k = k
1
−k
2
, which yields
d
3
k
1
2k
0
1
d
3
k
2
2k
0
2
=
1
2
1
(q
2
0
−k
2
0
)
d
3
q d
3
k . (10)
In the center-of-mass system of the lepton pair k
1
+k
2
= 0 =q we have
Q
2
=q
2
0
, k
2
0
= 0sothatwecanwrite
1
2
d
3
q
Q
2
d
3
k =
1
2
d
3
q
Q
2
dΩ
k
|
k
|
2
d
|
k
|
=
1
2
d
3
q d
|
k
|
dΩ
k
=
1
2
d
4
q dΩ
k
. (11)
The angle dΩ
k
= dφ
k
dcosθ
k
corresponds to the angle relative to the appropri-
ately chosen axis in the lepton-pair center-of-mass system. Putting everything
together we find
dσ =
α
2
2s
1
Q
4
L
µν
W
µν
1
(2π)
4
d
4
q dΩ
k
. (12)
As seen from (8) the Drell–Yan cross section is described by the hadronic
tensor in a quite analoguos way to the hadronic tensor in the case of deep in-
elastic lepton–nucleon scattering. In the case of Drell–Yan the current product
j
ν
(0) j
µ
(x) is sandwiched not in a one-nucleon state but in the two-nucleon state
|
NN
≡
|
p
1
p
2
. Hence a similar procedure as in the case of operator product ex-
pansion is not applicable here. However, we will use a procedure a little bit more
general to derive a factorization of the short-distance part from the long-distance
part. In leading order in the strong coupling constant we insert into the hadronic
tensor the vector currents
j
µ
(x) j
ν
(0) = e
2
q
q
i
(x)γ
µ
q
j
(x)q
l
(0)γ
ν
q
k
(0)δ
ij
δ
lk
, (13)
where we have made the dependence on the color denoted by the latin indices
i, j, k, l explicit. Performing a Fierz transformation
3
on the quark fields we can
write
q
j
(x)
α
q
l
(0)
β
=−
1
4
q
l
(0)q
j
(x)
δ
αβ
−
1
4
q
l
(0)γ
q
j
(x)
γ
αβ
−
1
8
q
l
(0)σ
σ
q
j
(x)
σ
σ
αβ
−
1
4
q
l
(0)γ
5
γ
q
j
(x)
γ
γ
5
−
1
4
q
l
(0)γ
5
q
j
(x)
γ
5αβ
(14)
3
See W. Greiner and B. Müller: Gauge Theory of Weak Interactions, 3rd ed. (Springer,
Berlin, Heidelberg, New York 2000).
Example 6.5

422 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
Example 6.5
and analogously for (−)q
k
(0)q
i
(x), where an additional minus sign is encoun-
tered due to the anticommuting fermion field operators. Note that the indices α, β
refer to the Dirac indices of the γ matrices. Thus (13) is transformed to
j
µ
(x) j
ν
(0) = e
2
q
δ
ij
δ
lk
−
1
16
$
tr
γ
µ
γ
ν
q
l
(0)q
j
(x)
q
i
(x)q
k
(0)
+tr
γ
µ
γ
γ
ν
γ
σ
q
l
(0)γ
q
j
(x)
q
i
(x)γ
σ
q
k
(0)
+tr
γ
µ
γ
5
γ
γ
ν
γ
5
γ
σ
q
l
(0)γ
γ
5
q
j
(x)
q
i
(x)γ
σ
γ
5
q
k
(0)
+
1
2
tr
γ
µ
σ
σ
γ
ν
σ
λη
q
l
(0)σ
σ
q
j
(x)
q
i
(x)σ
λη
q
k
(0)
+ tr
γ
µ
γ
5
γ
ν
γ
5
q
l
(0)γ
5
q
j
(x)
q
i
(x)γ
5
q
k
(0)
%
, (15)
where all other combinations lead to an odd number of γ matrices under the trace
and thus to zero.
Now the quark operators have to be factorized into the nucleon states. Only
color-less combinations will contribute. A Fierz transformation in color space
will achieve that. Using the relation
δ
ij
δ
lk
=
1
N
δ
jl
δ
ik
−2t
A
jl
t
A
ik
, (16)
with the SU(3) Gell-Mann matrices λ
A
/2 = t
A
and N = 3 the number of colors,
we find
W
µν
=
−
1
16
e
2
q
1
N
tr
γ
µ
γ
γ
ν
γ
σ
×
d
4
xe
iq·x
,
p
1
q(0)γ
q(x)
p
1
,
p
2
q(x)γ
σ
q(0)
p
2
+other terms . (17)
In this equation we have used that only the first part in (16) will give color-
less matrix elements and have not written down explicitely the other struc-
tures stemming from the expansion in (15). Only the vector matrix elements
p
1
|
q(0)γ
q(x)
|
p
1
will contribute at leading twist to unpolarized scattering.
To proceed further we specify our coordinate system. We choose two lightlike
vectors n
µ
and n
µ
with n
2
= n
2
= 0:
n
µ
=
1
√
2
(
1, 0, 0, −1
)
,
n
µ
=
1
√
2
(
1, 0, 0, 1
)
, n ·
n = 1 , (18)
so that in light-cone coordinates for any vector k
µ
n ·k =
1
√
2
k
0
+k
3
= k
+
,
n ·k =
1
√
2
k
0
−k
3
= k
−
. (19)

6.1 The Drell–Yan Process 423
The volume element in such coordinates reads d
4
k = dk
−
dk
+
d
2
k
⊥
,wherek
⊥
=
(k
x
, k
y
) is the transverse component of the vector k
µ
. We use the two lightlike
vectors n
µ
and n
µ
to fix the incoming momenta:
p
µ
1
= p
+
1
n
µ
,
p
µ
2
= p
−
2
n
µ
, (20)
and the virtual photon’s momentum q as
q
µ
= x
1
p
µ
1
+x
2
p
µ
2
+q
µ
⊥
. (21)
In the same way as the Lorentz vector q
µ
may be expanded in terms of two light-
cone vectors and a transverse component any γ matrix can be decomposed into
“plus” and “minus” and transverse directions:
γ
µ
=n/ ·n
µ
+n/ ·n
µ
+γ
µ
⊥
=n/
p
µ
1
p
+
1
+n/
p
µ
2
p
−
2
+γ
µ
⊥
. (22)
Such a decomposition normally is referred to as Sudakov decomposition.As-
suming that in (17) proton 1 travels in the “plus” direction and proton 2 in the
“minus” direction, we can approximate the matrix element as
,
p
1
q(0)γ
q(x)
p
1
∼
p
1
p
+
1
p
1
|
q(0)n/q(x)
|
p
1
, (23a)
p
2
|
q(x)γ
σ
q(0)
|
p
2
∼
p
2σ
p
−
2
p
2
|
q(x)n/q(0)
|
p
2
, (23b)
where all omitted contributions are of higher twist.
Further on we Fourier-transform the matrix elements
p
1
|
q(0)n/q(x)
|
p
1
=
d
4
r
1
(2π)
4
e
−ix·r
1
S(r
1
, p
1
), (24a)
p
2
|
q(x)n/q(0)
|
p
2
=
d
4
r
2
(2π)
4
e
−ix·r
2
S(r
2
, p
2
), (24b)
which after insertion into (17) leads to
W
µν
=
d
4
r
1
(2π)
4
d
4
r
2
(2π)
4
e
2
q
N
1
4
tr
γ
µ
p/
1
γ
ν
p/
2
(2π)
4
δ
4
(q −r
1
−r
2
)
×(−)
1
p
−
2
S(r
2
, p
2
)
1
p
+
1
S(r
1
, p
1
). (25)
Here we have succeded in writing the lepton pair production in NN scattering in
terms of a product of a part calculable in perturbation theory (the trace) together
with the δ function and the nonperturbative matrix elements
S(r
2
, p
2
), S(r
1
, p
1
),
which symbolically can be written as
W
µν
=
d
4
r
1
(2π)
4
d
4
r
2
(2π)
4
H
µν
(r
1
, r
2
, q)
˜
S(r
1
, r
2
). (26)
Example 6.5
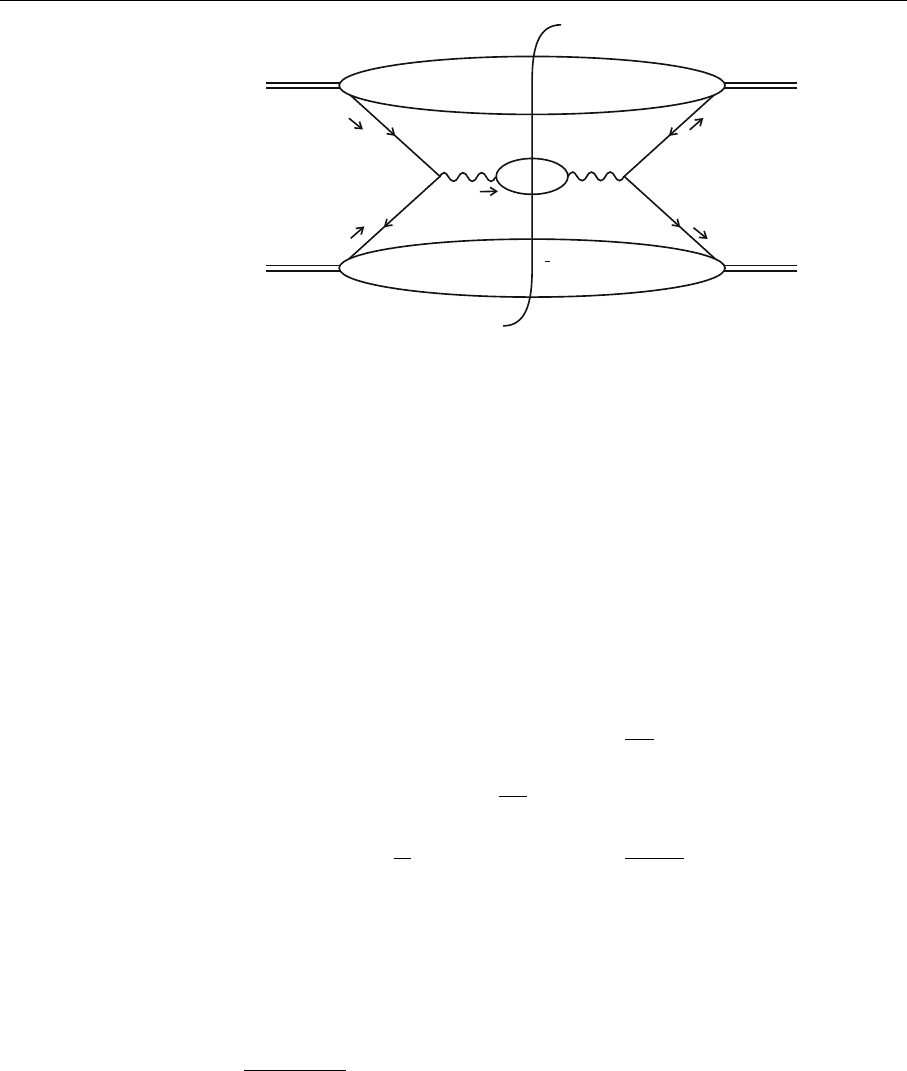
424 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
q
p
1
r
1
r
1
r
2
r
2
p
1
p
2
p
2
mn
S(r,p)
11
S(r,p)
22
Fig. 6.16. Diagram relevant
for the Drell–Yan process at
leading order QCD
Here H
µν
(r
1
, r
2
, q) is the part of the diagramm consisting of lines that carry the
“hard” momentum q
µ
while
˜
S(r
1
, r
2
) is the part that does not. See Fig. 6.16.
The leading contribution of the diagram arises when the momenta of the
quark lines entering into H
µν
(r
1
, r
2
, q) are on shell and collinear to p
1
and p
2
.
This can systematically be accounted for by expanding the hard part around its
collinear components. Approximating
r
1
≈ ζ
1
p
1
; ζ
1
=r
+
1
/ p
+
1
,
r
2
≈ ζ
2
p
2
; ζ
2
=r
−
2
/ p
−
2
, (27)
the hard part can be written as
H(r
1
, r
2
) = H(ζ
1
p
1
,ζ
2
p
2
) +(r
1
−ζ
1
p
1
)
∂
∂r
1
H(ζ
1
p
1
,ζ
2
p
2
)
+(r
2
−ζ
2
p
2
)
∂
∂r
2
H(ζ
1
p
1
,ζ
2
p
2
)
+
1
2!
(r
1
−ζ
1
p
1
)
(r
2
−ζ
2
p
2
)
σ
∂
2
∂r
1
∂r
σ
2
H(ζ
1
p
1
,ζ
2
p
2
)
+... . (28)
This procedure is known as collinear expansion
4
and in general is used to cal-
culate the 1/Q
2
correction terms to the parton model results. Here it will be
sufficient to obtain from the leading term in the expansion in (28) the parton
model already implemented in (6.6).
4
R.K. Ellis, W. Furmanski, and R. Petronzio: Nucl. Phys. B 207, 1 (1982); Nucl. Phys.
B 212, 19 (1983)
J. Qiu, G. Sterman: Nucl. Phys. B 353, 105 (1991).

6.1 The Drell–Yan Process 425
Restricting ourselves to the leading term in (28) means approximating the
δ function in (25) by
δ
4
(q −r
1
−r
2
) ≈ δ
4
(q −ζ
1
p
1
−ζ
2
p
2
)
=δ
2
(q
⊥
)δ(x
1
−ζ
1
)
1
p
+
1
δ(x
2
−ζ
2
)
1
p
−
2
. (29)
In the second step we have inserted the parametrization of the momentum q
(see (21)). Noting that
d
4
r
1
(2π)
4
d
4
r
2
(2π)
4
(2π)
4
δ
4
(q −ζ
1
p
1
−ζ
2
p
2
)
=
dζ
1
p
+
1
dζ
2
p
−
2
δ
2
(q
⊥
)
1
p
+
1
δ(x
1
−ζ
1
)
1
p
−
2
δ(x
2
−ζ
2
)
×
d
2
r
1⊥
(2π)
2
d
2
r
2⊥
(2π)
2
dr
−
1
(2π)
2
dr
+
2
(2π)
2
, (30)
i.e. all but two integrations now are independent from integrations over the hard
part, we can combine the six other integrations over the soft part
S(r
1
) =
d
4
x e
ir
1
·x
p
1
|
q(0)n/q(x)
|
p
1
, (31a)
S(r
2
) =
d
4
x e
ir
2
·x
p
2
|
q(x)n/q(0)
|
p
2
, (31b)
to get
W
µν
=
dζ
1
dζ
2
e
2
q
N
1
4
tr
γ
µ
p/
1
γ
ν
p/
2
1
p
+
1
p
−
2
(2π)
4
δ(q
2
⊥
)δ(ζ
1
−x
1
)
×δ(ζ
2
−x
2
)
1
2
dx
−
(2π)
e
+i p
+
1
ζ
1
x
−
,
p
1
q(0)n/q(x
−
)
p
1
×
−
1
2
dy
+
(2π)
e
−i p
−
2
ζ
2
y
+
,
p
2
q(0)n/q(y
+
)
p
2
, (32)
where in the last step it was noted that
dy
+
(2π)
e
+i p
−
2
x
2
y
+
,
p
2
q(y
+
)n/q(0)
p
2
=
dy
+
(2π)
e
−i p
−
2
x
2
y
+
,
p
2
q(0)n/q(y
+
)
p
2
(33)
due to translation invariance of the matrix elements
,
p
2
q(y
+
)n/q(0)
p
2
=
,
p
2
q(0)n/q(−y
+
)
p
2
. (34)
Example 6.5

426 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
Example 6.5
To make the relationship with the previous parton model predictions more
apparent we define
q(ζ
1
) =
1
2
dx
−
(2π)
e
i p
1
x
−
ζ
1
,
p
1
q(0)n/q(x
−
)
p
1
,
q(ζ
2
) =
−
1
2
dy
+
(2π)
e
−i p
2
y
+
ζ
2
,
p
2
q(0)n/q(y
+
)
p
2
. (35)
Apparently the bilocal operators along the light cone can be identified with
the quark distribution function we discussed earlier. Further p
+
1
p
−
2
= p
1
p
2
=
s/2, where s is the overall center-of-mass energy. Hence (33) can be given as
W
µν
=
dζ
1
dζ
2
[
ˆ
τ
µν
(ζ
1
,ζ
2
)q(ζ
1
)q(ζ
2
)
+
ˆ
τ
µν
(ζ
2
,ζ
1
)q(ζ
1
)q(ζ
2
)] , (36)
i.e. a convolution of some partonic cross section with quark distributions. Note
that we accounted for the fact that the antiquark can be picked up from either
proton 1 or proton 2. In our derivation we analyzed only the case in which the
antiparticle is picked up from proton 2. Comparing coefficients we see that
ˆ
τ
µν
is given by
ˆ
τ
µν
=
2e
2
q
NS
1
4
tr
γ
µ
p/
1
γ
ν
p/
2
(2π)
4
δ(q
2
⊥
)δ(ζ
1
−x
1
)δ(ζ
2
−x
2
)
=
2e
2
q
N(ζ
1
ζ
2
S)
ˆ
w
µν
(2π)
4
δ(q
2
⊥
)δ(ζ
1
−x
1
)δ(ζ
2
−x
2
), (37)
with the tree-level contribution from quark–antiquark scattering
ˆ
w
µν
=
1
4
pol
v(ζ
2
p
2
)γ
µ
u(ζ
1
p
1
)
2
=
1
4
tr
γ
µ
(ζ
1
p/
1
)γ
ν
(ζ
2
p/
2
)
. (38)
This completes our proof that the cross section for Drell–Yan pair production
can be factorized into a partonic part, which is calculable order by order in per-
turbation theory, and a soft hadronic part, which can be parametrized in terms of
quark distribution functions.
6.1 The Drell–Yan Process 427
EXERCISE
6.6 Collinear Expansion and Structure Functions
in Deep Inelastic Lepton–Nucleon Scattering
Problem. Apply the technique of the collinear expansion to the physical process
of deep inelastic lepton–nucleon scattering. Analyze the hadronic tensor
W
µν
=
1
(2π)
d
4
x e
−iq·x
,
pS
j
ν
(0) j
µ
(x)
pS
=−F
1
(x, Q
2
)g
µν
+F
2
(x, Q
2
)
p
µ
p
ν
p ·q
−i"
µνλσ
q
λ
p ·q
S
σ
g
1
(x, Q
2
) +O(q
µ
q
ν
) (1)
and express the structure functions F
1
and g
1
through bilocal operators defined
along the light cone.
Solution. As in the previous example we first define the kinematics by choosing
two lightlike vectors n
µ
and n
µ
so that n
2
=n
2
=0andn ·n = 1.
The momenta of the photon, q
µ
, and the target hadron, p
µ
, can then be
parametrized as
q
µ
=−xp
µ
+
Q
2
2xp
+
n
µ
, (2a)
p
µ
= p
+
n
µ
. (2b)
It is easy to convince oneself that indeed p
2
=0, q
2
=−Q
2
,andx = Q
2
/2pq
refers to the usual definition of the Bjorken scaling variable. The proton is chosen
to travel along the light cone in the + direction. We insert vector currents
j
µ
(x) =
f
e
f
q
f
(x)γ
µ
q
f
(x), (3a)
j
ν
(0) =
f
e
f
q
f
(0)γ
ν
q
f
(0) (3b)
into the hadronic tensor W
µν
and formally apply the Wick theorem. With this we
find
W
µν
=
e
2
2π
d
4
x e
−iq·x
,
pS
q(0)γ
ν
iS(−x)γ
µ
q(x)
+
q(x)γ
µ
iS(x)γ
ν
q(0)
pS
=
e
2
2π
d
4
x
d
4
k
(2π)
4
e
−i(q−k)·x
G
pS
q(0)γ
ν
i
k/
γ
µ
q(x)
pS
H
+ e
−i(q+k)·x
G
pS
q(x)γ
µ
i
k/
γ
ν
q(0)
pS
H
(4)
428 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
Exercise 6.6
where we have introduced the free-quark propagator
iS(−x) =
d
4
k
(2π)
4
e
ik·x
i
k/
=
d
4
k
(2π)
4
e
ik·x
ik/
k
2
+i"
(5)
and suppressed flavor indices. Shifting the variable of integration k → k +q
and performing a Fierz transformation as explained in the previous example we
arrive at
W
µν
=
e
2
2π
d
4
k
(2π)
4
1
4
tr
γ
ν
i
k/ +q/
γ
µ
γ
α
d
4
x e
ik·x
p
|
q(0)γ
α
q(x)
|
p
+
e
2
2π
d
4
k
(2π)
4
1
4
tr
γ
ν
i
k/ +q/
γ
µ
γ
α
γ
5
d
4
x e
ik·x
p
|
q(0)γ
5
γ
α
q(x)
|
p
+(q ↔−q;µ ↔ ν) . (6)
Note that these terms are the only ones that contribute. The other terms from the
Fierz transformation ∼1,γ
5
,σ
αβ
vanish due to an odd number of γ matrices un-
der the trace. Performing a Sudakov decomposition (see (22) of Example 6.5) of
the γ matrix,
γ
α
=n/n
α
+n/n
α
+γ
α⊥
=n/
p
α
p
+
+n/n
α
+γ
α⊥
≈n/
p
α
p
+
, (7)
the Dirac indices can be factorized in (6). In addition to that, we assume that the
parton momentum k
µ
is collinear to the parent hadron’s momentum:
k
µ
= x
1
p
µ
= x
1
p
+
n
µ
(8)
so that x
1
=k
+
/ p
+
.
With that all but one integration over k can be performed to give
W
µν
=
e
2
2π
dx
1
p
+
1
4
tr
γ
ν
i
x
1
p/ +q/
γ
µ
p/
p
+
×
dx
−
2π
e
ik
+
x
−
,
p
q(0)n/q(x
−
)
p
+
e
2
2π
dx
1
p
+
1
4
tr
γ
ν
i
x
1
p/ +q/
γ
µ
p/
p
+
γ
5
×
dx
−
2π
e
ik
+
x
−
,
pS|q(0)γ
5
n/q(x
−
)|pS
+(q ↔−q;µ ↔ ν) . (9)
As explained in more detail in the chapter on the GLAP equation we are inter-
ested in that part where intermediate particles are on shell. Thus instead of the
