Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


6.1 The Drell–Yan Process 399
so the correction to α can be written as
α →α
#
1 +
2α
s
3π
−ln
2
(β) −3ln(β) −
7
2
+
π
2
3
&
. (6.42)
The corresponding correction to the Drell–Yan cross section is
d∆σ
DY
(rad. −corr.)
dM
2
=
α
3π
1
0
dx
a
x
a
q
q
a
(x
a
)
¯
q
b
(x
b
) +
¯
q
a
(x
a
)q
b
(x
b
)
×
8παα
s
e
2
q
9M
2
−ln
2
(β) −3ln(β) −
7
2
+
π
2
3
. (6.43)
Adding this result to (6.37) gives the final result:
d∆σ
DY
(total)
dM
2
=
2α
s
3π
1
0
dx
a
x
a
q
q
a
(x
a
)
¯
q
b
(x
b
) +
¯
q
a
(x
a
)q
b
(x
b
)
×
4πα
2
e
2
q
9M
2
4
3
π
2
−
7
2
, (6.44)
which implies that the Drell–Yan cross section is just multiplied by a constant
factor, which can be identified with the K factor
K(1st order) = 1 +
2α
s
3π
4π
2
3
−
7
2
=1 +2.05 α
s
. (6.45)
If we insert α
s
≈0.3, we get K ≈ 1.6, which is already a good step towards the
experimental value K ≈ 2. Thus it can be hoped that the perturbative expression
will indeed converge to the correct K factor. One can continue by pursuing this
tedious calculation order by order. Instead we wish to address a much more fun-
damental approach, namely that it is often possible to sum up certain radiative
corrections exactly, i.e., to all orders in the coupling constant. Such techniques
are called “resummation techniques” and are a central issue of current research
in QCD. The idea is very simple. Sometimes corrections can be iterated and it
can be proven that the iteration has a very simple form, i.e. assumes the form of
an exponential or a geometric series. A geometric series we know already from
QED, where we resummed fermion bubbles. We have depicted the resummation
of fermion bubbles in Fig. 6.6. In the following, we will resum an exponential
series. The result will be that K is proportional to exp[2πα
s
(M
2
)/3], implying
that
K = exp
2
3
πα
s
M
2
1 −
2
3
πα
s
+
2α
s
3π
4π
2
3
−
7
2
= exp
2
3
πα
s
M
2
1 −α
s
2π
3
−
8π
9
+
7
3π
= exp
2
3
πα
s
M
2
1 −0.0446 α
s
. (6.46)

400 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
++ +
=
1
1-
Fig. 6.6. Resummation of
fermion bubblesin QED
Fig. 6.7. Illustration of the
origin of divergences in
(6.48)
This suggests an excellent convergence of the perturbative expansion after the
resummed exponential factor is isolated. Furthermore the numerical result for
α
s
≈0.25 −0.35,
K(1st order + resummation) = exp
2
3
πα
s
M
2
1 −0.0446 α
s
=1.7 −2.0 , (6.47)
agrees well with the empirical values. In fact (6.47) is further improved by also
taking into account the second order and serves then to determine α
s
(M
2
) or
Λ
QCD
. The starting point of the argument is as follows. The terms absorbed
into the exponent are the π
2
terms in (6.43) and (6.44). According to (6.40)
and (6.41) these arise from the analytic continuation of the logarithm to nega-
tive arguments. Thus it is sufficient to keep only the logarithmic terms to high
orders, to sum them up, and to continue them then to negative arguments. This
procedure is called “leading-logarithm approximation” (LLA) and is the stan-
dard procedure for resummation. Next we shall discuss the correction due to
gluon emission in the production of a quark–antiquark pair by a massive pho-
ton. The resummed corrections for the Drell–Yan process can then be obtained
from the result by analytic continuation. The calculation can be found in Exer-
cise 6.4. Here we simply give the result for the decay rate Γ of a massive photon
to a quark–antiquark pair +photon:
d
2
Γ
dx
1
dx
2
= 3αe
2
q
M
32α
s
3π
x
2
1
+x
2
2
(1 −2x
1
)(1 −2x
2
)
, (6.48)
where x
1
and x
2
are the energy fractions carried by the quark and antiquark. The
gluon energy fraction is x
3
=1 −x
1
−x
2
. We treat the decay of the massive pho-
ton in its rest frame, i.e., k
γ
=(M, 0, 0, 0). Obviously this expression diverges if
x
1
or x
2
approaches 1/2. This is obvious from Fig. 6.7 for the case x
1
→1/2. The
intermediate propagator becomes on-mass-shell, if
(k − p
1
)
2
=(M(1 −x
1
), 0, 0, −x
1
M)
2
= M
2
((1 −x
1
)
2
−x
2
1
)
= M
2
(1 −2x
1
) = 0 . (6.49)
For a finite gluon energy only x
1
or x
2
can be equal to 1/2. Thus (6.48) has two
leading, logarithmically diverging contributions: one for x
1
→1/2 and one for
x
2
→1/2. We change to the coordinates
t = ( p
2
+ p
3
)
2
= (k − p
1
)
2
= M
2
(1 −2x
1
),
z =
E
2
E
2
+E
3
x
1
→
1
2
=
E
2
1
2
M
=2x
2
, (6.50)

6.1 The Drell–Yan Process 401
4M
2
d
2
dx
1
dx
2
⇒
d
2
dt dz
, (6.51)
d
2
Γ
dt dz
=3αe
2
q
2α
s
3π
1 +z
2
t(1 −z)
=3αe
2
q
α
s
2πt
4
3
1 +z
2
1 −z
. (6.52)
The new variable z has obviously the meaning of the fraction of the energy of
the original quark state carried by the final quark state after gluon emission.
Therefore it is not suprising that we recover in (6.51) again the quark-splitting
function P
qq
(z) known from our derivation of the GLAP equations. As usual the
virtual corrrection adds effectively the ‘+’ prescription to the bracket in (6.52).
Let us now turn to multigluon emission. An important point to know is that for
the specific gauge we used in Exercise 6.4 only a single amplitude contributes,
namely S
22
. The sum of the three terms S
11
+S
22
+S
12
is of course independent
of the choice of gauge. However, choosing an appropriate gauge we can move
the contributions of each single diagram around, so that, as done in our case,
only S
22
contains a logarithmic divergence, i.e. we have chosen a gauge where
interference terms are absent (see figure).
The t integration leads to a logarithmic divergence. With (6.50) we get
S
11
= 8c
1 −2x
1
1 −x
2
= 8c
t
M
2
(1 −z)
(no logarithmic divergence),
S
22
= 8c
(1 +z
2
)M
2
t(1 −z)
(logarithmic divergence),
S
12
=−16c
1
1 −2x
2
=−
16c
1 −z
(no logarithmic divergence),
c = 4g
2
e
2
e
2
q
. (6.53)
Thus for the leading term the two-gluon emission probability is just the prod-
uct of two one-gluon emission probabilities. There are no interference effects.
This fact is intimately connected to the form of the GLAP equations. If inter-
ference effects were important, one would not get such a simple equation on the
level of distribution functions, i.e. probabilities. Therefore in leading logarithmic
approximation one simply gets
d
n
Γ
dz
1
...dz
n
dt
1
...dt
n
=3αe
2
q
α
s
(t
1
)
2πt
1
P
qq
(z
1
)
...
α
s
(t
n
)
2πt
n
P
qq
(z
n
)
.
(6.54)
We define the t
i
such that t
1
≥t
2
≥...≥ t
n
. Note that for our specific gauge only
those graphs in which the quark lines couple to gluons contribute in the LLA.
Graphs in which the antiquark couples to the gluons give no leading-log con-
tribution. This fact has no deep physical meaning but is exclusively due to the
specific gauge used. Equation (12) in Exercise 6.4 contains p
2
/x
2
and not p
1
/x
1
.
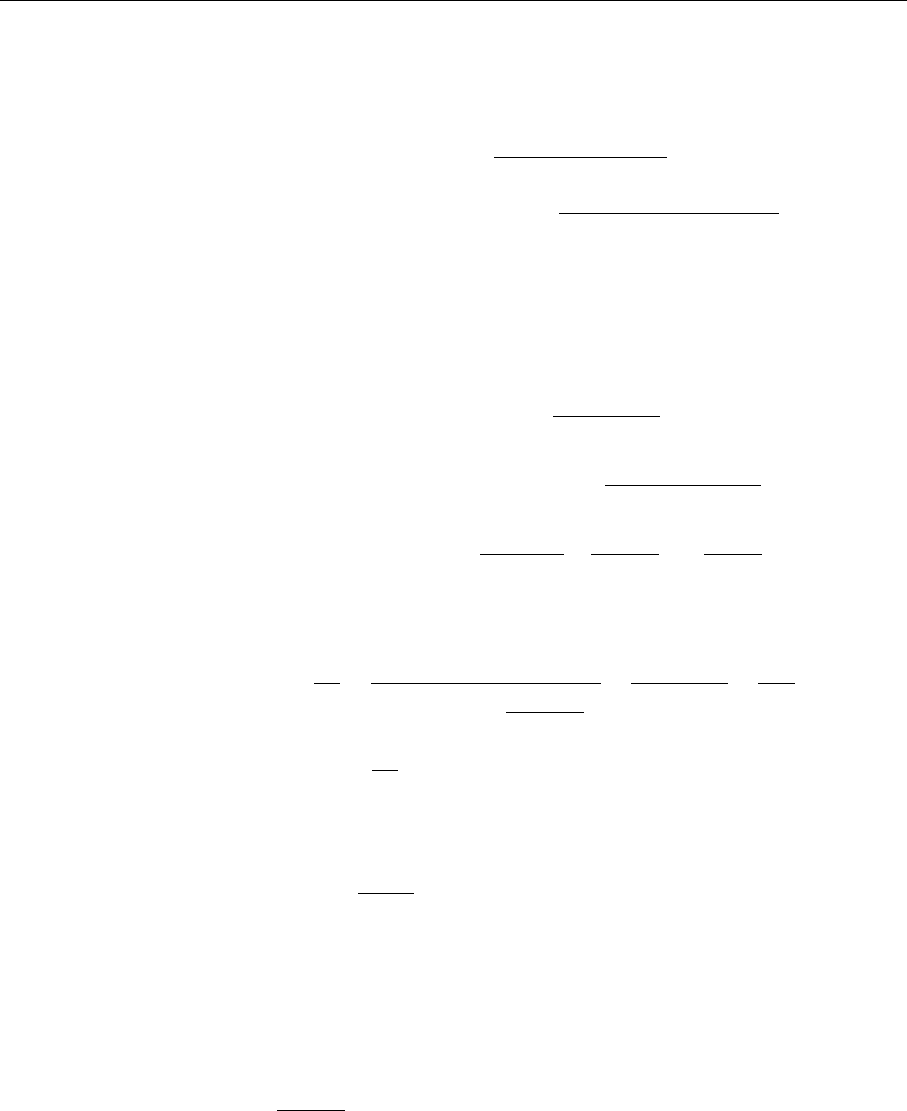
402 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
This asymmetry generates the asymmetry in the contributing processes. Now let
us define S(Θ) to be the probability that after n-gluon emissions the outgoing
quark still has a scattering angle p
⊥
/ p
"
<Θ, with p
"
and p
⊥
being defined with
respect to the jet axis, and the original quark momentum, respectively. For the
following we need the relation between t and the scattering angle θ. With
p
2
=
z(1 −x
1
)M, p
⊥
,
z
2
(1 −x
1
)
2
M
2
− p
2
⊥
, (6.55)
p
3
=
(1 −z)(1 −x
1
)M, −p
⊥
,
(1 −z)
2
(1 −x
1
)
2
M
2
− p
2
⊥
(6.56)
we find that [using p
2
⊥
(1 −z)
2
(1 −x
1
)
2
M
2
∼(1 −z
1
)
2
M
2
/4]
t = 2 p
2
· p
3
=2
)
z(1 −z)(1 −x
1
)
2
M
2
+ p
2
⊥
−
'
z(1 −x
1
)M −
p
2
⊥
2z(1−x
1
)M
(
×
'
(1 −z)(1 −x
1
)M −
p
2
⊥
2(1−z)(1 −x
1
)M
(*
≈2
p
2
⊥
+
p
2
⊥
(1 −z)
2z
+
p
2
⊥
z
2(1−z)
≈
p
2
⊥
(1 −z)
. (6.57)
We are interested in typical bremsstrahlung processes, i.e., z ≈ 1. For z → 0,
multigluon emission plays no role. The angle is related to p
⊥
by
ϑ ≈
p
⊥
p
"
p
⊥
z(1 −x
1
)M −
p
2
⊥
2z(1−x
1
)M
p
⊥
z(1 −x
1
)M
2p
⊥
M
<Θ (6.58)
⇒ p
2
⊥
<
Θ
2
4
M
2
. (6.59)
Remember that the leading-logarithm approximation (LLA) we are investigating
is only valid for x
1
≈1/2. As a consequence of (6.58) we find that
(1 −z)<
Θ
2
M
2
4t
. (6.60)
While S(Θ) relates to the probability that the quark is diverted by an angle less
than Θ we define the conjugate probability T(Θ) that the quark is diverted by
an angle greater than Θ,i.e.S(Θ) +T(Θ) = 1. The probability for the emission
of a gluon is given by the function d
2
Γ/ dt dz in (6.52). To find the total “decay
rate” we integrate over z and t with the integration bounds we can deduce from
(6.60). It holds that
Θ
2
M
2
4(1−z)
z=0
< t < M
2
, (6.61)
6.1 The Drell–Yan Process 403
where the maximal momentum transfer t is bounded by the total mass of the
gluon. From (6.60) it follows that
1 −
Θ
2
M
2
4z
< z < 1 : S(Θ) (6.62)
which relates to the probability S(Θ) that the emission takes place with an angle
smaller than Θ. The conjugate probability T(Θ) that the emission occurs with
angle greater than Θ is given by the other values of z,
0 < z < 1−
Θ
2
M
2
4z
: T(Θ) , (6.63)
so that we find
S
1
(Θ) = 1 −T
1
(Θ) = 1 −
M
2
Θ
2
M
2
/4
dt
1−Θ
2
M
2
/4t
0
dz
2α
s
3π
1 +z
2
t(1 −z)
z→1
≈ 1 −
4α
s
3π
M
2
Θ
2
M
2
/4
dt
1−Θ
2
M
2
/4t
0
dz
1
t(1 −z)
=1 −
4α
s
3π
M
2
Θ
2
M
2
/4
dt
1
t
−ln
Θ
2
M
2
4t
=1 −
4α
s
3π
−ln
Θ
2
4
ln(t) +
1
2
ln
2
t
M
2
M
2
Θ
2
M
2
/4
=1 −
4α
s
3π
ln
2
Θ
2
4
−
1
2
ln
2
Θ
2
4
=1 −
2α
s
3π
ln
2
Θ
2
4
. (6.64)
For T(Θ) one does not have to treat the subtleties of the radiative corrections can-
celing the infrared divergencies for t →0, z → 1. For finite Θ the integrals for
T
1
(Θ) are finite. The probability is strongly peaked toward θ Θ. Therefore we
can approximate
S
n+1
(Θ)
S
n
(Θ)
∼1 −T
1
(Θ) , (6.65)
which results in
S
n
(Θ) ∼
1 −T
1
(Θ)
n
. (6.66)
We still have to correct for the fact that the t
j
were ordered according to
t
1
≥t
2
≥t
3
...≥t
n
, (6.67)
404 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
Fig. 6.8. Comparison of the
gluonic corrections for two
Drell–Yan processes
so that only one of the n! permutations contained in (6.65) is chosen:
S
n
(Θ) ∼
1
n!
1 −T
1
(Θ)
n
. (6.68)
With (6.67) we can now easily sum the gluon emission to all orders:
S(Θ) ∼
n
S
n
(Θ) = e
1−T
1
(Θ)
= e ×exp
−
2
3
α
s
π
ln
2
Θ
2
4
. (6.69)
Obviously this still lacks the proper normalization factor. For T
1
(Θ) ≡ 0, S(Θ)
must clearly be equal to one. Thus the missing normalisation factor is e
−1
and
the final expression reads
S(Θ) = exp
−
2
3
α
s
π
ln
2
Θ
2
4
= exp
−
2
3
α
s
π
ln
2
p
⊥min
M
2
. (6.70)
This expression has the structure of a form factor and is usually interpreted as
such. It is then called “Sudakov form factor”. Clearly (6.69) suppresses the emis-
sion of collinear soft gluons, rendering the cross sections finite. The Sudakov
form factor is probably the best-known example of resummation in QCD and is
of great phenomenological importance in describing jet formation correctly. As
we shall discuss at the end of this section the renormalization group equation
imposes the condition that the exponential must always be of the form (6.69).
The only problem remaining is to find the correct analytic continuation for the
given dynamics. In our case this is relatively easy. Figure 6.8 compares the graph
for which we have calculated (6.68) with the gluon corrections to the Drell–Yan
cross section. Obviously the outgoing gluons just have to be substituted by in-
coming ones. This corresponds to the analytic continuation to z ≥ 1 rather than
z ≤ 1. According to (6.59) this is equivalent to the continuation Θ
2
→−Θ
2
,
which in turn implies that
exp
#
−
2
3
α
s
π
Re
ln
2
Θ
2
4
&
⇒ exp
#
−
2
3
α
s
π
−π
2
+ln
2
Θ
2
4
&
⇒exp
2
3
α
s
π
exp
−
2
3
α
s
π
ln
2
Θ
2
4
. (6.71)
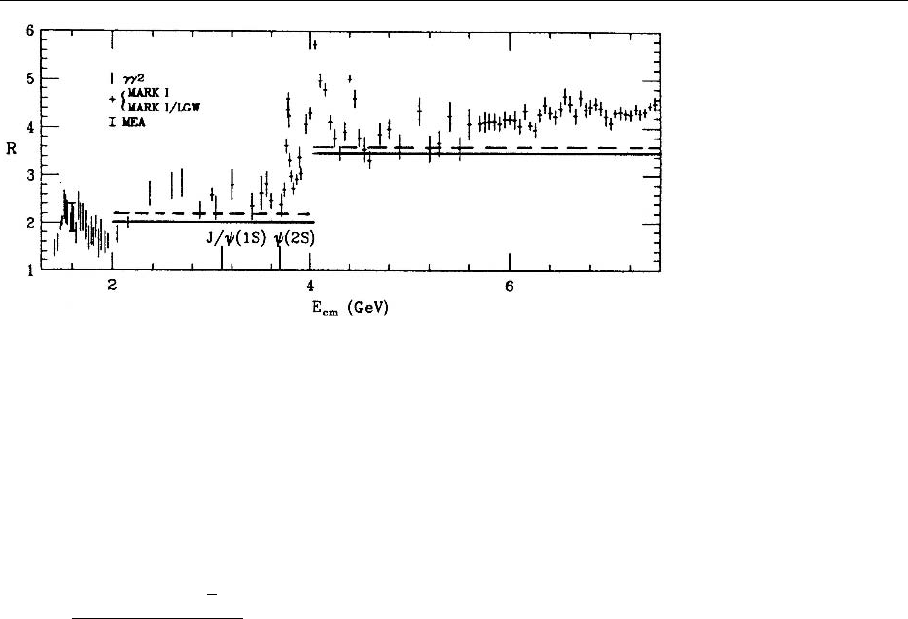
6.1 The Drell–Yan Process 405
Fig. 6.9. The prediction of
the parton model for the
Drell–Yan process includ-
ing QCD corrections. The
data are taken from Review
of Particle Properties, Phys.
Rev. D 45 (1992)
As we have integrated over t respectively Θ the second factor is contained in the
α
s
corrections in the last bracket in (6.46). The remaining exponential factor is
indeed exp(2πα
s
/3) as stated in (6.46).
The appearence of this factor is a typical property of higher-order corrections
and the standard result of resummation. The same result can be obtained with the
more formal apparatus of the renormalization group equation.
To complete this chapter let us add a few brief remarks on the phenomenol-
ogy of the Drell–Yan process. As discussed in Sect. 4.2, the parton model
predicts quite simple behavior for the total cross section:
R =
σ
e
+
e
−
→qq
σ
e
+
e
−
→µ
+
µ
−
=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
2 E
cm
> 2GeV
10/3 E
cm
> 4GeV
11/3 E
cm
> 10 GeV
. (6.72)
We have just discussed the K factor that describes the resummed QCD correc-
tions to this process. We sketch in Fig. 6.9 how these corrections improve the
agreement with the data. The QCD corrections increase R, i.e., the K factor is
always larger than 1. The change in the theoretical prediction for R has been
includedinFig.6.9(atΛ = 2 GeV). To obtain a truly precise prediction, QED/
radiative corrections, higher QCD corrections, mass corrections, and so on must
also be included. These increase R somewhat more, in particular for small E
cm
.
Figure 6.9 shows that the parton-model predictions are in general slightly too
low while the QCD-corrected results clearly give a better description of the data.
In this comparison one must take into account that in some energy regions the
presence of resonances can induce large variations of R.
Choosing a special subgroup of the Drell–Yan processes, one can perform
a far more specific test of QCD. This has been done most successfully for 3-jet
events, which are characterized by the property that most of the energy is carried
by hadrons, leading to three narrow and clearly distinguished angular regions.
The simplest process that can lead to a 3-jet event is the gluon bremsstrahlung
whose graph is shown in Fig. 6.7. However, not all bremsstrahlung events are
identified as 3-jet events, but only those in which the angle between gluon jet
and quark jets is sufficiently large. Conversely, the graph
406 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
also contributes to 3-jet events, as long as one gluon jet is not resolved from the
others. Finally the simplest Drell–Yan process,
contains, with a certain statistical weight, events with unbalanced momen-
tum distributions generated by the nonperturbative process of hadronization.
A calculation of the 3-jet probability and a determination of the strong coupling
constant α
s
is therefore an extensive and model-dependent venture. See Fig. 6.10
for a typical 3-jet event.
Fig. 6.10. A typical 3-jet
event in the laboratory sys-
tem
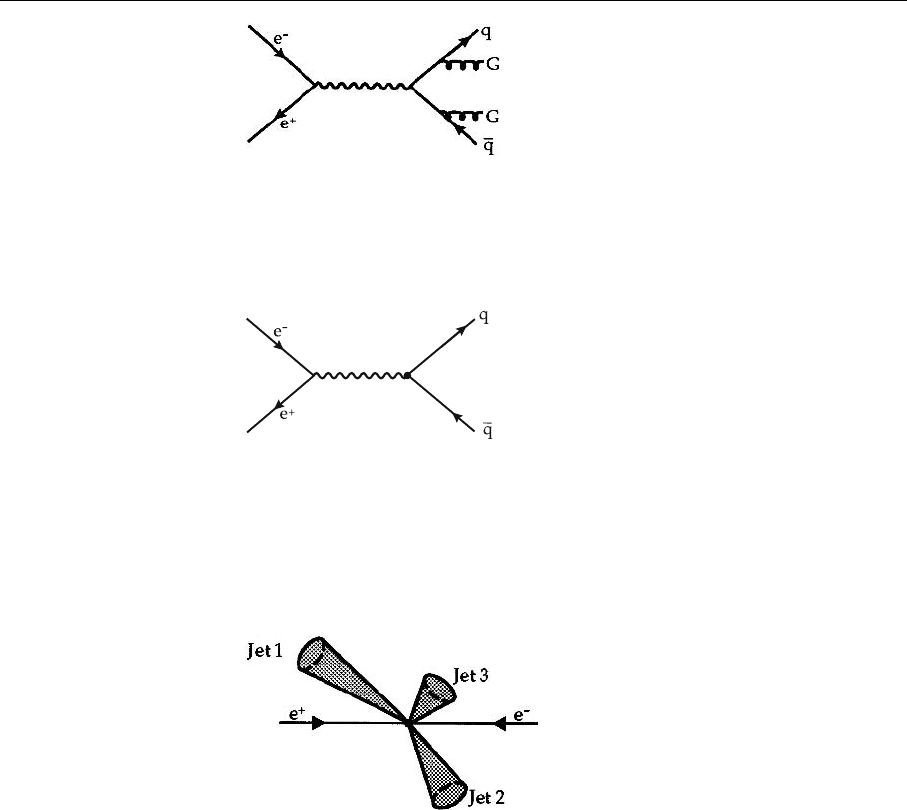
A typical calculation goes like this.
1. One calculates elementary QCD processes in perturbation theory. To order α
2
s
,
these are the graphs of Fig. 6.11, for example.
2. One calculates hadronization using one or more of the special computer codes
developed for this purpose. These programs are based on some basic assump-
tions about the creation and decay of color strings between separating quarks
(see Fig. 6.12). A typical code of this type depends on a substantial number of
parameters and gives good fits for a large number of processes.
3. Finally one determines by the experimentally used definition of 3-jet events
the corresponding contribution to this class of events. Here also experimental
sensitivities enter.
6.1 The Drell–Yan Process 407
Fig. 6.11a–c. Elementary
graphs of the Drell–Yan pro-
cess up to order α
2
s
Fig. 6.12. Creation and
break-up of a color string
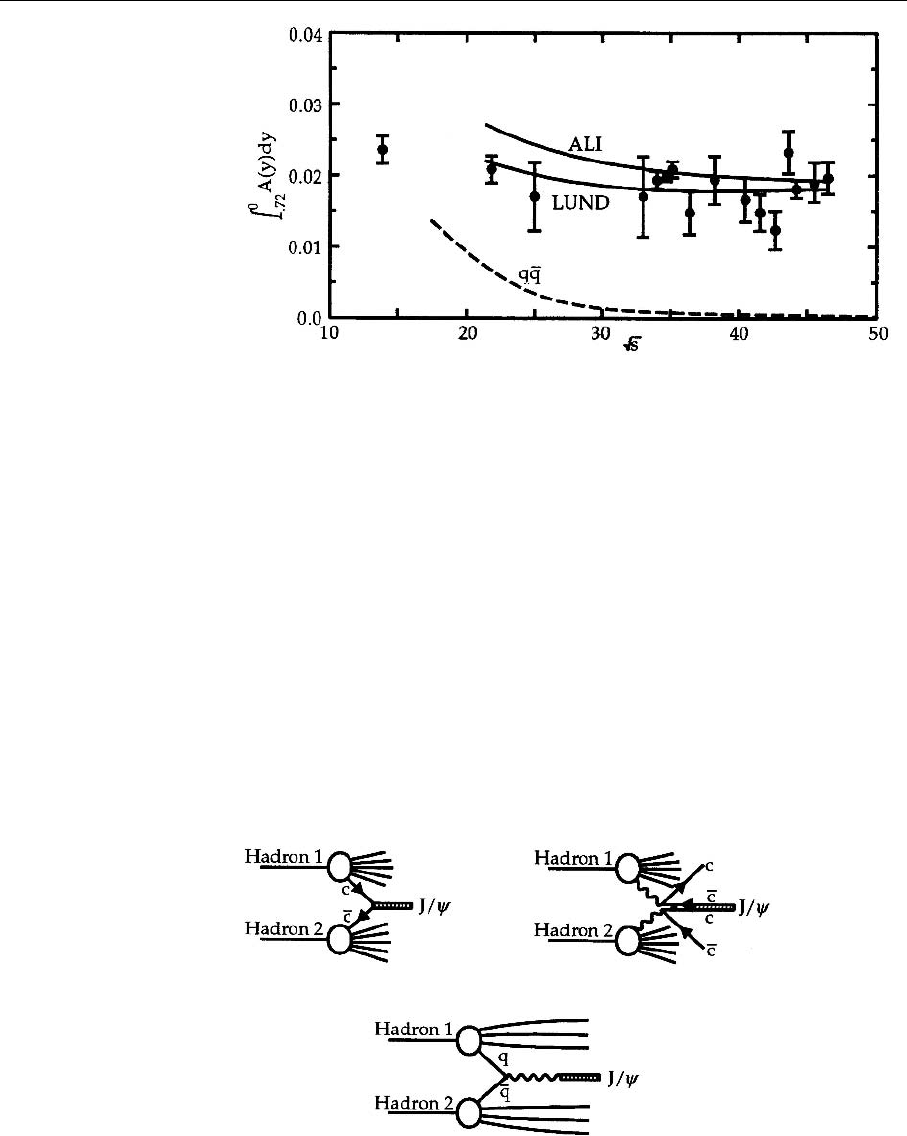
The result of Fig. 6.13 was obtained in this way.
2
Here the energy asymmetry
(whose exact definition is not important to us) is shown against the total center-
of-mass energy. The two curves result from different hadronization programs.
The coupling constant used was
α
s
=
12π
(33 −2N
f
) ln
Q
2
Λ
2
⎧
⎨
⎩
1 −
6(153 −19N
f
)
(33 −2N
f
)
2
ln
ln
Q
2
Λ
2
ln
Q
2
Λ
2
⎫
⎬
⎭
(6.73)
with N
f
=5andΛ =100 MeV.
Equation (6.73) is the correct form of the running coupling constant when
two-loop processes are taken into account. As the Drell–Yan process is calcu-
lated to order α
2
s
, the coupling constant must also be determined to this order, to
be consistent.
2
See M. Chen: Int. J. Mod. Phys. A 1, 669 (1986).
408 6. Perturbative QCD II: The Drell–Yan Process and Small-x Physics
Fig. 6.13. The fit of ex-
perimental 3-jet events with
Λ =100 MeV. LUND and
ALI denote the two hadron-
ization routines used
Fig. 6.14. Charmonium cre-
ation in hadron–hadron re-
actions
Using this fit to determine Λ gives
Λ = 100 ±30
+60
−45
MeV or α
s
(E
cm
= 44 GeV) = 0.12 ±0.02 . (6.74)
Other analyses give somewhat different values for Λ. We do not want to enter
this controversy here; we simply wanted to illustrate the procedure used.
In a similar way one attempts to describe semi-exclusive hadron–hadron scat-
tering processes with hadrons in the final state. But here the uncertainties and
model-dependence is even larger, so that frequently nothing more than rather
general statements result. Such statements may concern, for example, the power
of Q
2
with which a specific cross section decays. These processes are there-
fore less important as tests of QCD, with the exception of specific reactions like
charmonium production (see Fig. 6.14).
The Drell–Yan process offers a number of possible ways to tests QCD.
Although the results are quite convincing as a whole, their quality bears no com-
parison with tests of QED or of the Glashow–Salam–Weinberg model. Another
