Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

368 5. Perturbative QCD I: Deep Inelastic Scattering

Example 5.16

operator, and one twist-4 operator. However, sometimes some operators vanish

by equations of motions, i.e. i

D/ψ = mψ ∼ 0 for massless quarks. For instance

the twist-4 operator is actually zero for a massless quark state. Sometimes, ma-

trix elements of operators are zero due to trivial arguments. For example, if we

were to sandwich the twist-3 operator between nucleon states





−i







= V



− P



=0(5)

it is evident that we would not be able to parametrize it in terms of a reduced

matrix element. Due to the vector character of the object we have to parametrize

it with P

(due to Lorentz covariance this is the only vector at hand), which

obviously cannot be antisymmetrized. On the other hand, the operator





−i







= A



− P



(6)

exists. Due to the presence of γ

we can parametrize it with the spin vector S

which is an axial vector.

Now we take a look at a physical example. Performing the operator product

expansion as we did before, but taking all trace terms carefully into account (and

not only the free quark propagator) we could derive the ﬁrst moment of the spin

dependent structure function g

and obtain the following formula

dxg

(x, Q

) =

(0)



(2)

+4d

(2)

+4 f

(2)







. (7)

Here the reduced matrix elements are deﬁned as:

twist-2



ψγ





=2S

(0)

, (8)

twist-3





βσ

+γ

ασ







−traces =

(2)





+2P

− P

−P

− P



−traces



, (9)

twist-4



ψg

αβ





= 2M

(2)

. (10)

B. Ehrnsperger et al.: Phys. Lett. B 150, 439 (1994)

5.6 The Spin-Dependent Structure Functions 369

Here we have a list of nontrivial twist-2, twist-3, and twist-4 operators. For the

twist-3 operator one has to subtract traces so that the operator has well-deﬁned

spin. Explicitely they look like the following

traces (l.h.s. of (9)) =+

PS|



αβ

σµ

ασ

βµ

βσ

αµ



ψ|PS  ,

traces (r.h.s. of (9)) =+



αβ

βσ

ασ



The twist-2 operator is a two-particle correlator, i.e. it can be interpreted as

a probability distribution; see Fig. 5.32. Schematically it can be represented as

the square of an amplitude.

Fig. 5.32. Very schematic

graphical representation of

a twist-2 operator. See also

Fig. 5.17, which we dis-

cussed previously. The blob

represents the nucleon state

PS

PS, the dashed lines

the factorization scale

For twist-3 and twist-4 operator s this is not the case. Higher twists in

general are correlations of more than two particles. In our case we have a quark–

gluon–quark correlation. The gluon (g

µν

) is of different origin compared

to the perturbative gluonic contribution that lead to the α

expansion we dis-

cussed before. It is of nonperturbative nature and depends on the structure of the

nucleon.

In the special case of the higher twist contributions to the ﬁrst moment of

we can make the physical meaning of higher twist even more explicit. In the

rest frame of the nucleon P

=(M

, 0), S

= (0, S) we can write the operator

Fig. 5.33. Schematic graph-

ical representation of a high-

er twist operator in DIS. The

gluon, represented by the

curled line, couples to the

nucleon state and not to an

other perturbative quark line

Example 5.16

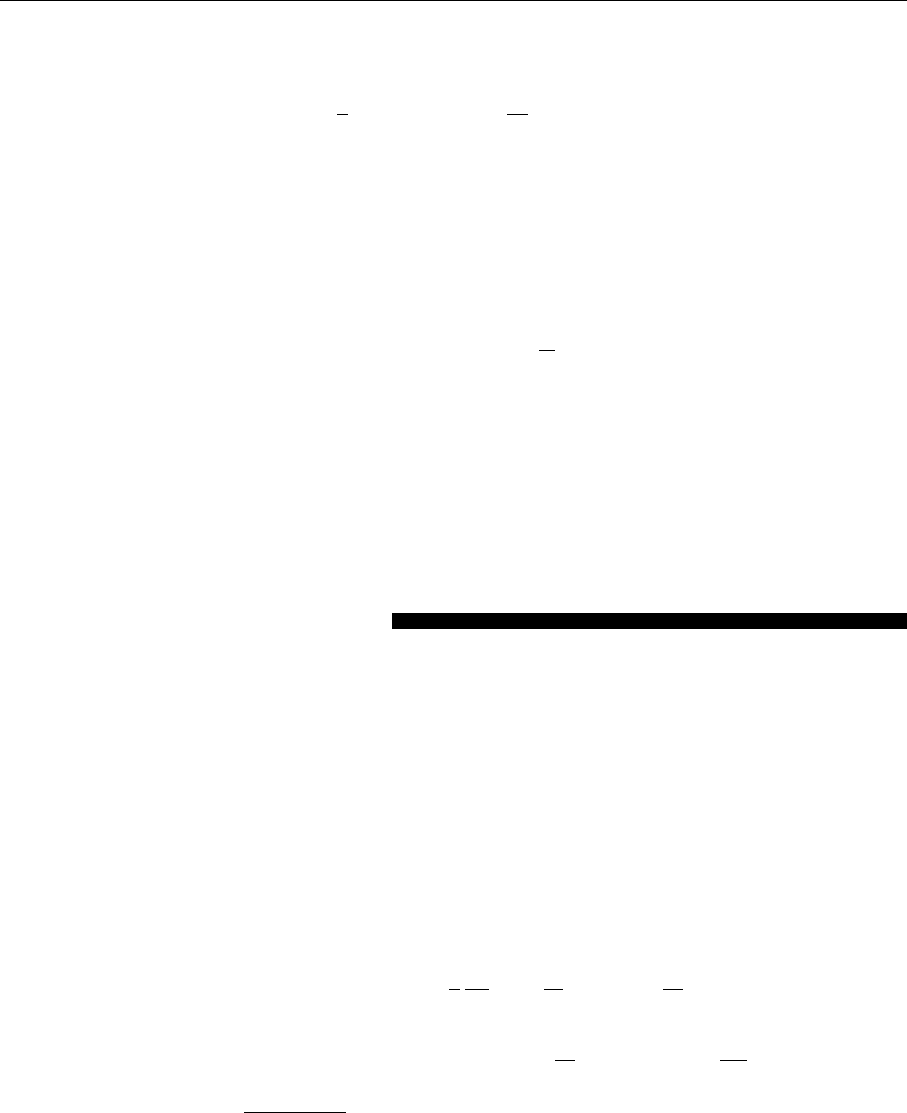
370 5. Perturbative QCD I: Deep Inelastic Scattering

Example 5.16

determining f

(2)

and d

(2)

in components using the dual ﬁeld strength tensor

µν

µνσ

σ

aµν

⎛

⎜

⎝

0 −B

−B

0 E

−E

0 E

−E

⎞

⎟

⎠

(11)



−B

(

×E

)





= 2M

(2)

(12)

and



(

×E

)





=8M

(2)

(13)

with the quark current j

=−gψγ

/2ψ and color-electric and color-

magnetic ﬁeld strength E

and B

. The quark current in the nucleon induces an

electric ﬁeld. This induced ﬁeld contributes to the spin of the nucleon. Clearly,

correlations like that are well beyond the simple parton model. That is one of

the reasons why theoreticians like to deal with higher twist, because of the in-

sight gained into the structure of the nucleon. Moreover, present experiments are

reaching such precision that even 1/Q

corrections in DIS are accessible. Recent

progress has been made to analyze higher twist beyond the level of the lowest

moments. We will discuss this approach in the next example.

EXAMPLE

5.17 Perturbation Theory in Higher Orders and Renormalons

In the previous section we learned how to calculate perturbative corrections to

structure functions measured in deep inelastic scattering (DIS). While this was

quite an easy task for the ﬁrst-order correction to F

, higher-order corrections

become increasingly difﬁcult to handle. Up to now, third-order corrections for

the lowest moments of some structure functions are available. As an example,

we quote the corrections to the ﬁrst moment of the nonsinglet polarized structure

function g

, the Bjorken sum rule, i.e. the difference between the proton structure

function g

and the neutron structure function g

(see also Sect. 5.6 on the

spin-dependent structure functions):

dxg

p−n

(x, Q

) =



1 −

−3.5833





−20.2153





+...







. (1)

S.A. Larin, J.A.M. Vermaseren: Phys. Lett. B 259 (1991) 345.

5.6 The Spin-Dependent Structure Functions 371

First we notice that the numerical values of the expansion coefﬁcient increase,

a phenomenon not only observed in this special case.

In general, perturba-

tive series in interacting quantum ﬁeld theories are regarded as divergent rather

than as convergent series. Observing the phenomenological success of pertur-

bation theory in QED, for instance the calculation of the anomalous magnetic

moment of electron and muon, one interpretes the divergent series as an asymp-

totic one. That means, even if the series does not converge it still makes sense

up to a certain order. This order naturally depends on the numerical magnitude

of the expansion parameter. While in QED α = 1/137 is a rather small number

even a factorial divergent coefﬁcient, e.g. like n!α

, would lead to the explosion

of the terms only for n  136 (check this!). The situation is different in QCD,

where α

= 1GeV

) ≈ 0.4 is much larger. One therefore has to be careful

to decide up to which order the expansion really makes sense and whether the

divergence of the series may be seen already at low orders. An asymptotic ex-

pansion is only meaningful up to a certain order, which usually is the smallest

term in the expansion. This minimal term is deﬁned as the term of order n

the expansion. Terms of higher order, i.e. terms with n > n

of the series, start

to increase:



The truncated series may be written as

R(Q

) =

−1



n=0

±r

−1



n=0

±∆R(Q

), (2)

where α

= α

). The uncertainty in the approximation, characterized by the

quantity R(Q

) that we would like to calculate in perturbation theory, is given

by the minimal term. As we will see in the following, it can be shown that the

uncertainty does not depend logarithmically on Q

but has a power behavior

∆R(Q

) ∼





, (3)

where s is some integer number.

We normally attribute the same 1/Q

dependence to higher-twist corrections.

Let us consider the quantity R(Q

) in some more detail. In general we can write

it in the general form

R −R

tree

+···+r

k+1

+... , (4)

G. ’t Hooft in The Whys of Subnuclear Physics, ed. by A. Zichichi (Plenum, New York

1977).

A.H. Müller: The QCD Perturbation Series in QCD – Twenty Years Later, ed. by P.M.

Zerwas and H.A. Kastrup (World Scientiﬁc, Singapore, 1922), p. 162.

Example 5.17

372 5. Perturbative QCD I: Deep Inelastic Scattering

Example 5.17

where we have already subtracted the contribution of the tree-level term ∼ α

that the expansion starts at order α

. Using the integral representation of k!

∞

dte

−t

= k! (5)

we can write

R −R

tree

∞



m=0

m+1

∞

dte

−t

. (6)

Interchanging integration and summation gives

R −R

tree

∞

dte

−t

∞



m=0

(

)

∞

due

−u/α

∞



m=0

∞

due

−u/α

[

]

(u) (7)

with u = α

t. In the last step we deﬁned the Borel representation of the series as

[

]

(u) =

∞



m=0

. (8)

The Borel representation can be used as a generating function for the ﬁxed-order

coefﬁcients

[

]

(u)|

u=0

. (9)

But, more importantly, (7) is now taken as the deﬁnition of the summed series.

Even if the series in the expansion (4) is, in fact, divergent, with the help of the

Borel transformation we may be able to give it a unique value. This is not always

possible, of course. But if this is possible the series is said to be Borel summable.

As a simple example we consider the series which diverges factorially but with

alternating sign r

=(−)

n!. The Borel transformed series reads

1 −u +u

−u

±···=

1 +u

(10)

and its integral representation is well deﬁned,

∞

−u/α

1 +u

∞



m=0

(−)

n!α

. (11)

5.6 The Spin-Dependent Structure Functions 373

If, on the other hand, we have a series with a ﬁxed sign factorial growth r

∼n!

the transformed series reads

1 +u +u

+···=

1 −u

(12)

and in the integral representation we have to integrate over the pole at u =1. The

series therefore acquires an imaginary part and the integral is deﬁned only via

its principal value. Such a series as in (12) is referred to as not Borel summable.

In general a series exhibiting factorial growth of the coefﬁcients leads to singu-

larities in the complex Borel plane. Singularities on the negative real axis are

integrable, singularities on the positive real axis are not. The QCD perturbation

theory is not Borel summable: singularities on the positive real axis are present.

One ﬁnds singularities at the following positions.

• Instanton–antiinstanton singularities (instantons–antiinstantons are classical

solutions of the QCD equations of motion

) They can be found at u =

4π, 8π,... and are simply due to a classical effect. The number of diagrams

grows factorially with the order of the perturbative expansion.

• Renormalon singularities. As opposed to the instanton–antiinstanton singular-

ities that are due to the overall number of diagrams, there are single diagrams

that contribute a factor n! at order n to the amplitude. Diagrams of this kind

are those where a simple gluon line is replaced by a fermion bubble chain (see

Fig. 5.34). In QED these are exactly the diagrams that lead to the running of the

coupling constant. In general, if we substitute for the ﬁxed coupling at the vertex

the running coupling

) =

)

1 +β

) ln(k

)

, (13)

we ﬁnd that integration over the loop momenta k leads to a factorial growth of

the expansion coefﬁcient. In (13) β

is given by

4π



N −



(14)

where N = 3 for QCD (SU(3)) and zero for QED. N

is the number of ﬂavors.

To show that the running coupling constant leads to n! growth we con-

sider a dimensionless quantity that is calculated from a loop integration over

with Euclidean momentum k

=−k

(see Sect. 4.3):

I(Q

) =

f(k

, Q

)α

), (15)

G. ’t Hooft in The Whys of Subnuclear Physics, ed. by A. Zichichi (Plenum, New York

1977).

A.H. Müller: The QCD Perturbation Series in QCD – Twenty Years Later, ed. by P.M.

Zerwas and H.A. Kastrup (World Scientiﬁc, Singapore, 1922), p. 162.

Example 5.17

p+q

p+q-k

p-k

Fig. 5.34. Diagram that

leads to corrections to the

photon–quark vertex and di-

verges as n!

374 5. Perturbative QCD I: Deep Inelastic Scattering

Example 5.17

where Q

is the external momentum and f(k

, Q

) some function. Assuming

> Q

we can expand f(k

, Q

) in terms of Q

and ﬁnd

∼

∞





)



∞





(

−β

)





)

n+1



∞

(t)

−m

(−β

)

(t)α

)

n+1



∞

dye

−my

(−β

)

n+1





−



∞

dxe

−x

7 89 :

)

n+1

∼





−β



n!α

)

n+1

. (16)

The alternating sign factorial growth (β

> 0 in QCD) leads to singularities in

the complex Borel plane at

u =−

; m = 1, 2,... . (17)

Due to its origin from high virtualities (k

 Q

) these singularities are called

ultraviolet renormalons.

Considering the case of small loop momenta k

< Q

and expanding the

integrand in k

we get

∼





)







(

−β

)





)

n+1

∼







n!α

)

n+1

. (18)

The corresponding singularities at the positive axis in the Borel plane are called

infrared renormalons. They lie at u =+m/β

, m = 1, 2,... (see Fig. 5.35).

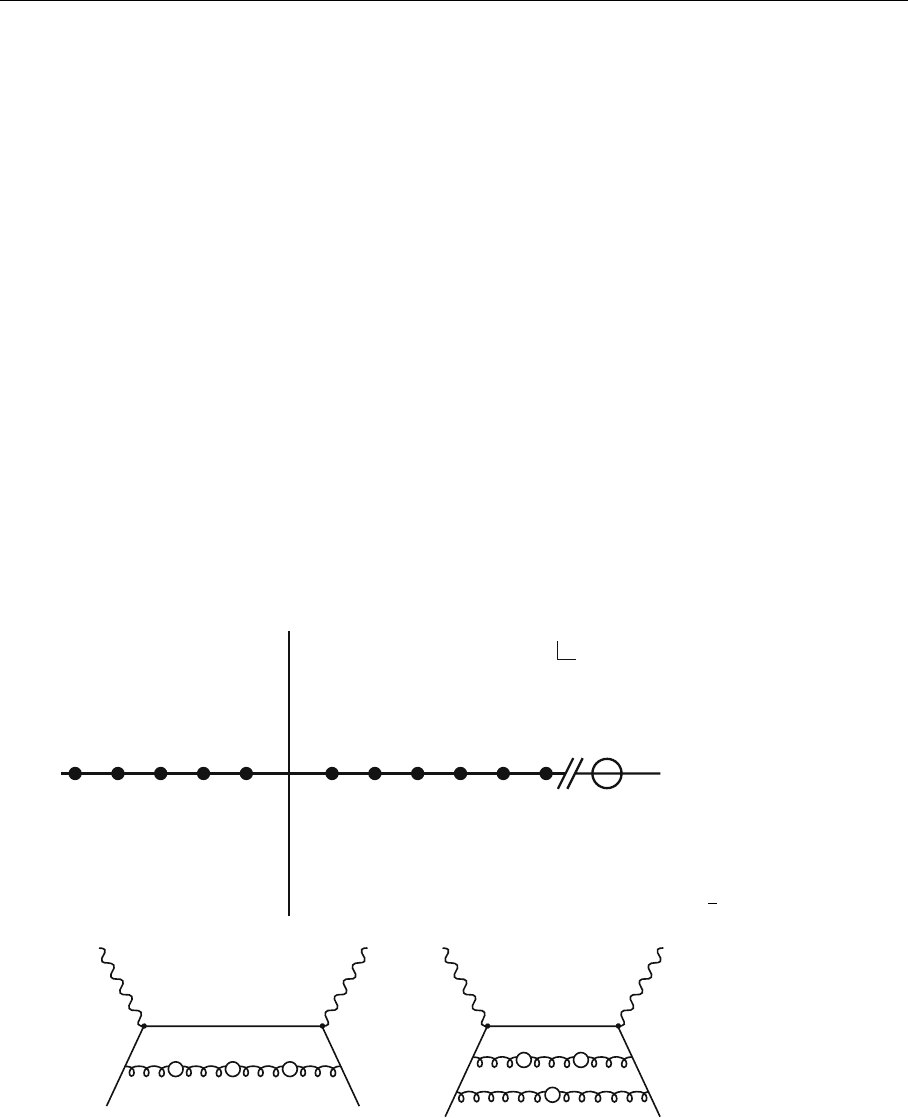
5.6 The Spin-Dependent Structure Functions 375

Having explained what renormalons are, we turn to the calculation of the

poles in the Borel plane, for instance for the perturbative expansion of the

Bjorken sum rule in (1). For that purpose let us consider once more the expan-

sion in (4). Each coefﬁcient r

can be written as an expansion in N

, the number

of active ﬂavors:

(0)

(1)

+···+r

(k)

. (19)

The different terms in the N

expansion are due to Feynman diagrams that

contain fermion bubbles . Each fermion bubble contributes a factor N

The leading term in the expansion (19), i.e. the term with the highest power

of N

, comes from an uncut bubble chain. Two fermion bubble chains, con-

taining k

and k

bubbles respectively, sublead in α

, i.e. they contribute at

order r

(k)

k−1

(see the Fig. 5.36). In our example both diagrams are of order N

but the one on the right-hand side with two bubble chains contains one additional

factor α

as compared to the left-hand diagram.

Diagrams that contain only one bubble chain are relatively straightforward

to evaluate and are those that lead to the renormalon. Such a calculation – taking

only fermion bubbles into account and neglecting all gluon–gluon interactions –

is a simple QED calculation, and the exactly calculated

(k)

(20)

coefﬁcient can be used as the starting point to approximate a QCD calculation.

I-I

UV renormalons IR renormalons

Fig. 5.35. Singularities in

the Borel plane. For asymp-

totically free theories (β

0) the IR renormalons can

be found on the positive

axis, the UV renormalons on

the negative axis. Instanton–

antiinstanton singularities

I) are on the positive axis

~ N

α ~ N

Fig. 5.36. Corrections to the

Compton forward scattering

amplitude: Double fermion

lines containing in total the

same number of bubbles are

subleading in N

as com-

pared to uncut fermion lines

Example 5.17

376 5. Perturbative QCD I: Deep Inelastic Scattering

Example 5.17

In QED the summed fermion bubble chains are the only diagrams that con-

tribute to the running of the coupling. Ward identities connect vertex correction

( p, p) and self-energy



( p) via the relation −∂/∂ p



( p) = Γ

( p, p) so

that the sum of all contributions their divergencies cancel and therefore do not

have to be renormalized.

In QCD also gluon and ghost bubbles contribute so that the one-loop β func-

tion gets a positive sign as opposed to the QED β function. The idea is then

simply to perform a QED calculation with the QED β function and, afterwards,

to substitute the QCD β function for the corresponding QED piece. The latter is

essentially given by (14) with N =0. In the QCD case N =3 and we substitute

for N

in (19)

(

11 −4πβ

)

(21)

and write the expansion (19) in terms of β

.Thisgives

(0)

(1)

+···+

(k)

, (22)

where the leading term of the β

expansion is given by

(k)

(

−6π

)

. (23)

Now we set all subleading (exact) coefﬁcients of the β

expansion (22) to zero

and get, in leading order β

(and therefore also in leading order N

≈

(k)

(−6πβ

)

(k)



−



(k)

k−1



−



·k +···+r

(k)



−



, (24)

where we substituted (−6πβ

) = N

−33/2 according to (21). In that way

we obtained approximations for the unknown subleading coefﬁcients that are

much harder to calculate exactly as compared to r

(k)

. This procedure is called

Naive Non-Abelianization (NNA).

To test how well this procedure works

we write the Bjorken sum rule with explicit N

dependence.

For example,



k−1

(−33/2)kr

(k)



approximates the term r

(k−1)

in (19). One should empha-

size that there is no deep justiﬁcation for this procedure. Instead it should be

considered as a toy model to study the behavior of perturbation theory in QCD

M. Beneke: Nucl. Phys. B 405, 424 (1993), D.J. Broadhurst: Z. Phys. C 58, 339

(1993).

S.A. Larin, J.A.M. Vermaseren: Phys. Lett. B 259 (1991) 345.

5.6 The Spin-Dependent Structure Functions 377

at large orders.

dxg

p−n

(x, Q

) =



1 −







−4.58+









−41.439 +7.61N

−0.177N



+...



1 −

−3.5833





−20.215





+...

, (25)

where the last line was derived for N

= 3. This agrees with (1). Substituting for

the highest power of N

,(N

and N

) N

→ N

−33/2, we ﬁnd

dxg

p−n

(x, Q

NNA



1 −







−5.5+









−48.188 +5.841N

−0.177N



+...



1 −

−4.5





−32.26





+...

, (26)

which reproduces the sign and the order of magnitude of the exactly calculated

coefﬁcients amazingly well.

In the following we explain a simple way to calculate the contributions from

bubble chains. The idea is extremly simple and rests on the observation that the

Borel transform of the bubble chain (or running coupling) is an extremly simple

function.

We therefore do not calculate each bubble contribution separately but instead

calculate the Borel transform of the whole bubble chain. The effective gluon

propagator with the insertion of fermion, gluon, and ghost bubbles reads

µν

) = iδ



−k

µν



(µ

)

1 +β

(µ

) ln



−k

/µ

−C



(27)

where we multiplied the gluon propagator, given in Landau gauge , with the run-

ning QCD coupling at scale k

, the momentum which runs through the gluon

line. The reference scale is µ

and will only at the end be set to Q

as in (13).

The factor e

−C

accounts for scheme dependence and is −5/3intheMS scheme

(MS stands for minimal subtraction).

In that scheme not only the 1/" pole but

also the contribution 1/" −γ

+ln(4πµ

) is subtracted.

J. Brodsky, G.P. Lepage, P.B. Mackenzie: Phys. Rev. D 28, 228 (1983).

Example 5.17