Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


358 5. Perturbative QCD I: Deep Inelastic Scattering
frame are
p
µ
=(E
e
, 0, 0, p
e
), P
µ
=(E
p
, 0, 0, −P
p
)
s
µ
e
(longitudinal) =±( p
e
, 0, 0, E
e
) ·
1
m
,
s
µ
p
(longitudinal) =±( p
p
, 0, 0, −E
p
) ·
1
M
,
s
µ
e
(transverse) =±(0, 1, 0, 0) and ±(0, 0, 1, 0),
s
µ
p
(transverse) =±(0, 1, 0, 0) and ±(0, 0, 1, 0). (5.289)
We recognize that the following products are large:
s
e
(l) ·s
p
(l) ≈±2
E
e
E
p
mM
, s
e
(l) · P ≈±2
E
e
E
p
m
. (5.290)
All the other scalar products in (5.288) are considerably smaller. Thus to meas-
ure spin-dependent structure functions, longitudinally polarized leptons must be
scattered off longitudinally or transversely polarized nucleons. This property can
also be seen from projecting on physical degrees of freedom of the photon in-
stead of summing over photon polarizations. In this case, the hadronic scattering
tensor is contracted with ε
∗
µ
ε
ν
.Hereε is the polarization vector of the virtual pho-
ton. In order for spin-dependent terms to be able to contribute, this expression
must contain an antisymmetric part. As can easily be checked, this is the case
only for longitudinal polarization vectors, e.g., it holds for
ε
µ
= (0, 1, i, 0)/
√
2thatε
∗
1
ε
2
=−ε
∗
2
ε
1
. (5.291)
A longitudinally polarized photon is most readily emitted by a longitudinally
polarized lepton. For other lepton polarizations its coupling is suppressed by
exactly the kinematic factors of (5.288).
In the experiments performed up to now, a longitudinally polarized proton
target has been used, and the asymmetry
A =
d
2
σ
dE
dΩ
(↑↑) −
d
2
σ
dE
dΩ
(↑↓)
d
2
σ
dE
dΩ
(↑↑) +
d
2
σ
dE
dΩ
(↑↓)
(5.292)
has been measured.
Inserting (5.289) into (5.288) one finds, for longitudinal polarization,
A
1
= D
)
g
1
(x) −
2Mx
Ey
g
2
(x)
F
1
(x)
+η
6
2Mx
Ey
g
1
(x) +g
2
(x)
F
1
(x)
*
, (5.293)
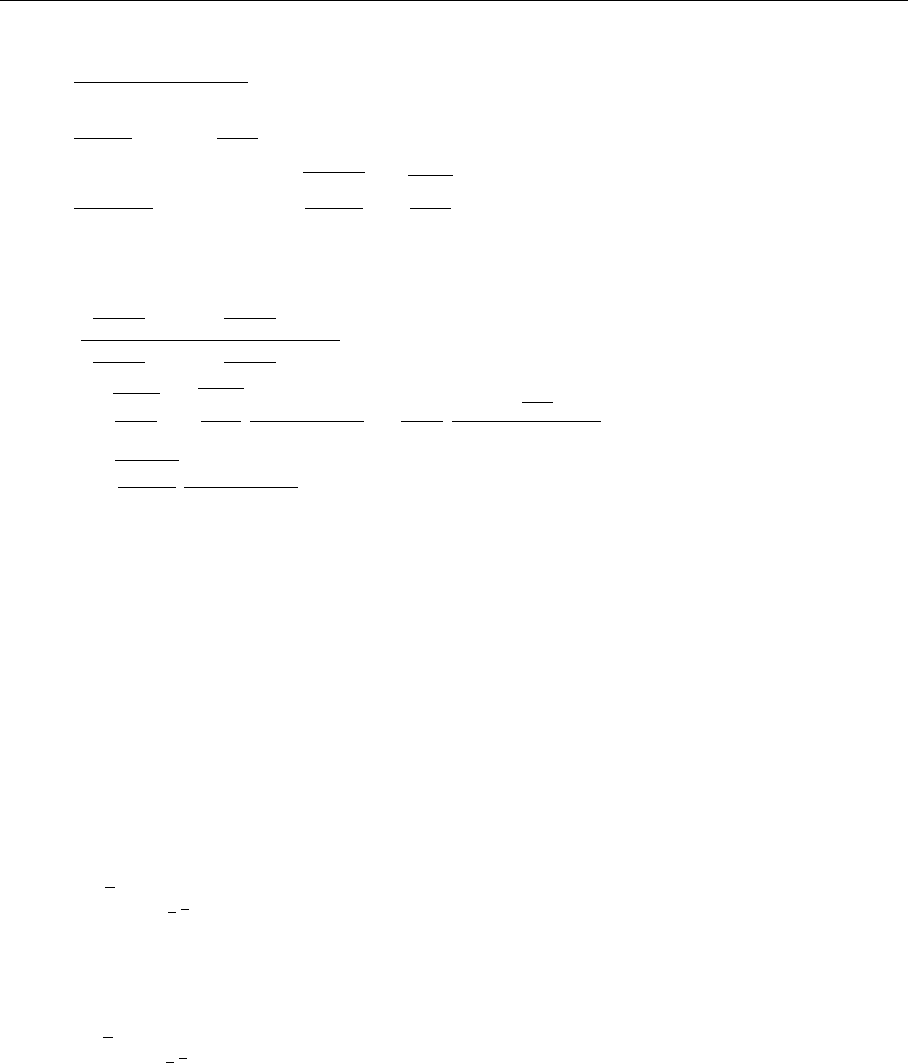
5.6 The Spin-Dependent Structure Functions 359
with
D =
y(2−y)
y
2
+2(1 −y)(1 + R)
,
y =
E −E
E
, R =
σ
γ
∗
L
σ
γ
∗
T
,
η =
2γ(1 −y)
2 − y
, and γ =
6
Q
2
M
2
ν
2
=
6
2Mx
Ey
. (5.294)
For transverse proton polarization the resulting asymmetry reads
A
2
=
d
2
σ
dE
dΩ
(↑→) −
d
2
σ
dE
dΩ
(↓→)
d
2
σ
dE
dΩ
(↑→) +
d
2
σ
dE
dΩ
(↓→)
= D
!
2ε
1 +ε
6
2Mx
Ey
g
1
(x) +g
2
(x)
F
1
(x)
−η
1 +ε
2ε
g
1
(x) −
2Mx
Ey
g
2
(x)
F
1
(x)
−→
!
2Mx
E −E
g
1
(x) +g
2
(x)
F
1
(x)
for Q
2
→∞, y → 1 (5.295)
with ε =(1 −y)/(1−y +y
2
/2). Since the cross sections for transverse and lon-
gitudinal polarization should be of approximately the same size, we deduce that
g
2
(x) is certainly not larger than g
1
(x). Therefore the contribution of g
2
(x) at
longitudinal polarization is suppressed by a factor Mx/E and constitutes only
a small correction. The asymmetry A
2
therefore measures mainly the ratio of
g
1
(x) to the unpolarized structure function F
1
(x). Next, there is the question
of whether g
1
(x) can be given a practical meaning like F
1
(x)?Thisisindeed
the case. To see this, it is sufficient to compare the hadronic and the leptonic
scattering tensor of (5.285) and (5.287), respectively.
Obviously each Dirac particle gives a contribution with the same form as that
proportional to G
1
multiplied by the probability to find a quark with the fitting
momentum fraction x and the right polarization. Accordingly, one obtains, in
analogy with the parton interpretation of F
1
,
F
1
(x) =
1
2
q=u,d,u,d...
q(x)Q
2
q
, (5.296)
where q(x) is the probability of finding a quark q with momentum fraction x,
a similar expression for g
1
(x)
g
1
(x) =
1
2
q=u,d,u,d...
Q
2
q
q
↑
(x) −q
↓
(x)
. (5.297)
Here q
↑
(x) indicates the probability of finding a quark with a momentum frac-
tion x polarized in the same direction as the whole proton. The asymmetry
360 5. Perturbative QCD I: Deep Inelastic Scattering
Fig. 5.29. The relationship
between deep inelastic scat-
tering and the forward ma-
trix element
measured is a measure of the distribution of the proton spin among its con-
stituents.
One of the most important properties of unpolarized structure functions is
that the momentum fraction deduced from them, which is carried by the quarks,
accounts for only half of the total momentum. This is striking evidence for the
existence of gluons. Analogously, from polarized structure functions we can ask
how much of the proton spin is carried by quarks, how much by gluons and how
much is present in angular momentum. This question has, up to now, not been
uniquely answered. The present experimental data have caused strong theoret-
ical discussions and led to the design of much improved and completely new
experiments. In the near future, experiments of the type
e
↑
(long.) +p
↑
,
3
He
↑
, d
↑
(long. or trans.) →e
+X ,
e
↑
(long.) +p
↑
,
3
He
↑
, d
↑
(long. or trans.) →e
+π
±
+X ,
p +p
↑
(trans.) → γ + X plus many more channels (5.298)
should be performed. In addition, polarized proton–proton collisions are
a possibility for the future.
This field is extremely active right now and a more detailed discussion of
the current situation is not suitable for a textbook. Instead, we consider two par-
ticular aspects where crucial concepts of QCD can be exemplified. As it turns
out, nearly all techniques of QCD are, in a nearly singular manner, important in
analyzing spin structure.
In particular, we consider the following aspects of the discussion.
1. The Bjorken and Ellis–Jaffe sum rule: From the knowledge of the axial vec-
tor coupling in weak interactions, predictions based on isospin and SU(3) flavor
symmetry for
+
dx(g
p
1
(x) −g
n
1
(x)) and
+
dxg
p
1
(x) can be obtained. This is
a nice example that flavor symmetry continues to play an important role even
after the introduction of color SU(3).
2. The axial anomaly and the gluonic contribution to g
1
(x): The axial anomaly
plays a major role for hadronic physics in general. We met it in Sect. 4.2 when re-
viewing the foundations of QCD and will show in Exercise 7.2 its importance in
understanding lattice QCD. As it turns out, the anomaly can contribute to the spin
structure function in a subtle manner. The analysis of this effect gives exquisite
insight into the physical meaning of the anomaly.

5.6 The Spin-Dependent Structure Functions 361
Let us start by discussing the Bjorken sum rule. The antisymmetric (spin-
dependent) part of the hadronic scattering tensor can be written as an axial-vector
forward matrix element of the proton (see Fig. 5.29). As the proton couples
to quarks we find that the spin-asymmetric part of the cross section ∆σ is
proportional to
iγ
µ
p/
γ
ν
ε
µναβ
= p
σ
g
µσ
γ
ν
+g
σν
γ
µ
−g
µν
γ
σ
+iε
µσνλ
γ
λ
γ
5
i ε
µναβ
= p
σ
ε
µνσλ
ε
µναβ
γ
λ
γ
5
=−2p
σ
g
α
σ
g
β
λ
−g
β
σ
g
α
λ
γ
λ
γ
5
=−2p
α
γ
β
γ
5
+2 p
β
γ
α
γ
5
, (5.299)
where we have used the well-known decomposition of the product of three
gamma matrices. Thus we find that
∆σ ∼
q
,
p s
Q
2
q
¯
q γ
α
γ
5
q
p s
. (5.300)
It is important to note that, owing to the optical theorem, we have obtained
a forward cross section, i.e., the momentum transfer is zero. In contrast, the
momentum transfer in the lepton–hadron scattering reaction q
µ
is very large,
but squaring this diagram to obtain the cross section leads to a graph in which
the second photon removes the momentum transferred by the first. (This is just
a description of the content of the optical theorem.) Thus this forward matrix
element can be related by isospin symmetry to a corresponding matrix element
between neutron and proton. More precisely we write
Q
2
=
15
18
+
1
3
τ
3
=
)
4
9
for the up quark
1
9
for the down quark
, (5.301)
implying that
∆σ
p
−∆σ
n
∼
1
3
,
N s
τ
3
¯
q γ
α
γ
5
q
N s
, (5.302)
where N =
p
n
is the usual nucleon doublet. Now we can introduce τ
+
τ
−
+
τ
−
τ
+
= 11; we obtain
∆σ
p
−∆σ
n
∼
1
3
-
N s
τ
+
τ
−
+τ
−
τ
+
τ
3
¯
q γ
α
γ
5
q
N s
.
=
1
3
-
N s
τ
+
τ
−
−τ
−
τ
+
¯
q γ
α
γ
5
q
N s
.
=
1
3
,
p s
τ
+
¯
q γ
α
γ
5
q
n s
+ h.c.. (5.303)
This, however, is just the weak-interaction matrix element of neutron beta decay.
The corresponding coupling is just g
A
/g
V
. Putting all the constants together, we
endupwith
1
0
dx
g
p
1
(x) −g
n
1
(x)
=
1
6
g
A
g
V
. (5.304)

362 5. Perturbative QCD I: Deep Inelastic Scattering
This is the famous Bjorken sum rule, which allows us to connect the proton and
the neutron results. It is strictly valid for Q
2
→∞. Various perturbative and
higher-twist corrections have been calculated:
1
0
dx
g
p
1
(x, Q
2
) −g
n
1
(x, Q
2
)
=
1
6
g
A
g
V
1 −
α
s
π
−
43
12
α
s
π
2
+
M
2
Q
2
1
0
dxx
2
2
9
g
p
1
−g
n
1
(x, Q
2
) +
4
3
g
p
2
−g
n
2
(x, Q
2
)
+
4
9
M
2
Q
2
( f
2u
− f
2d
) +
4
9
M
2
Q
2
(d
2u
−d
2d
) (5.305)
with
2(M
2
)
2
f
2q
s
σ
=
,
P S
g
¯
q
˜
G
σλ
γ
λ
q
P S
, q = u, d . (5.306)
The matrix element d
2
is defined in Example 5.16. The f
2q
can be calcu-
lated, for example, by QCD sum rule techniques and turn out to be small.
Also the d
2q
have been estimated and they are expected to give measurable
contributions.
22
The mass correction is small, basically because of the factor x
2
which suppresses the small x contributions.
Thus the Q
2
dependence of the Bjorken sum rule is well under control. It is
especially noteworthy that no anomalous dimension, i.e., no factor of the form
[α(Q
2
)/α(Q
2
0
)]
−d/2b
, occurs on the right-hand side of (5.305). This fact has
a simple physical reason. The main part of the Q
2
evolution of unpolarized struc-
ture functions is due to the many quark–antiquark pairs that contribute at high
Q
2
(see Fig. 5.23). Because the vector coupling to gluons conserves helicity,
these quark pairs are, however, predominantly unpolarized. In fact a double spin
flip is needed to obtain a polarized q
¯
q pair, and except for very small values of
x this is completely suppressed. Consequently the zeroth moment of g
p
1
, g
n
1
,
g
p
2
, g
n
2
should show only a very mild Q
2
dependence. (Actually there is good
reason to believe that
+
g
2
(x) dx ≡0.) Now, assuming that the strange quarks
are unpolarized, which is actually a very controversal assumption, we can ob-
tain the Ellis–Jaffe sum rule from (5.305). From the definition of g
1
(x) we have,
assuming strict isospin symmetry at the quark level, which is also controversial,
1
0
dxg
p
1
(x) =
1
2
4
9
∆u +
1
9
∆d
,
22
E. Stein, P. Gornicki, L. Mankiewicz, A. Schäfer and W. Greiner, Phys. Lett. B 343,
369 (1995).
5.6 The Spin-Dependent Structure Functions 363
1
0
dxg
n
1
(x) =
1
2
4
9
∆d +
1
9
∆u
, (5.307)
where ∆u, ∆d are the fractions of the proton spin carried by the u and d quarks,
respectively.
The Bjorken sum rule (5.304) implies that
1
0
dxg
p
1
(x) −
1
0
dxg
n
1
(x) =
1
6
∆u −∆d
=
1
6
g
A
g
V
,
∆u = ∆d +
g
A
g
V
, (5.308)
which is already one constraint. Still another constraint comes from the coup-
ling of s and u quarks in hyperon decays. To understand this we have to review
a little group theory. The general axial vectorial flavor SU(3) matrix element
B|S
5
jσ
|B
can be analyzed with the equivalent of the Wigner–Eckhardt theo-
rem. Here B, B
are baryon states from the flavor octet, σ is the Lorentz index,
and j = 1,... ,8 is the index of the SU(3) generator. We find that
p | S
5
jσ
| p =c ·n
σ
⎡
⎣
⎛
⎝
88
I =
1
2
I
3
=−
1
2
I =
1
2
I
3
=
1
2
Y =−1 Y = 1
8
1
I
j
−I
3 j
−Y
j
⎞
⎠
A
1
+
⎛
⎝
88
I =
1
2
I
3
=−
1
2
I =
1
2
I
3
=
1
2
Y =−1 Y = 1
8
2
I
j
−I
3 j
−Y
j
⎞
⎠
A
2
⎤
⎦
×
⎛
⎝
88
I
j
−I
3 j
I
j
I
3 j
−Y
−j
Y
j
1
0
⎞
⎠
. (5.309)
The isoscalar factors are listed.
23
A peculiarity of the SU(3) group is the appear-
ance of two unequivalent octet representations. This is related to the fact that
three octets can be coupled either by the symmetric d
abc
or the antisymmetric
f
abc
structure constants. It leads to the definition of two constants, D and F:
,
N
S
5
3σ
N
=c ·n
σ
√
30
40
A
1
+
√
6
24
A
2
=: c ·n
σ
D +F
,
D =
√
30
40
A
1
, F =
√
6
24
A
2
. (5.310)
Every axial-vector matrix element coupling two baryon states from the octet is
thus proportional to a specific combination of D and F and can therefore be used
23
See J.J. de Swart: Rev. Mod. Phys. 35 (1963) 916.
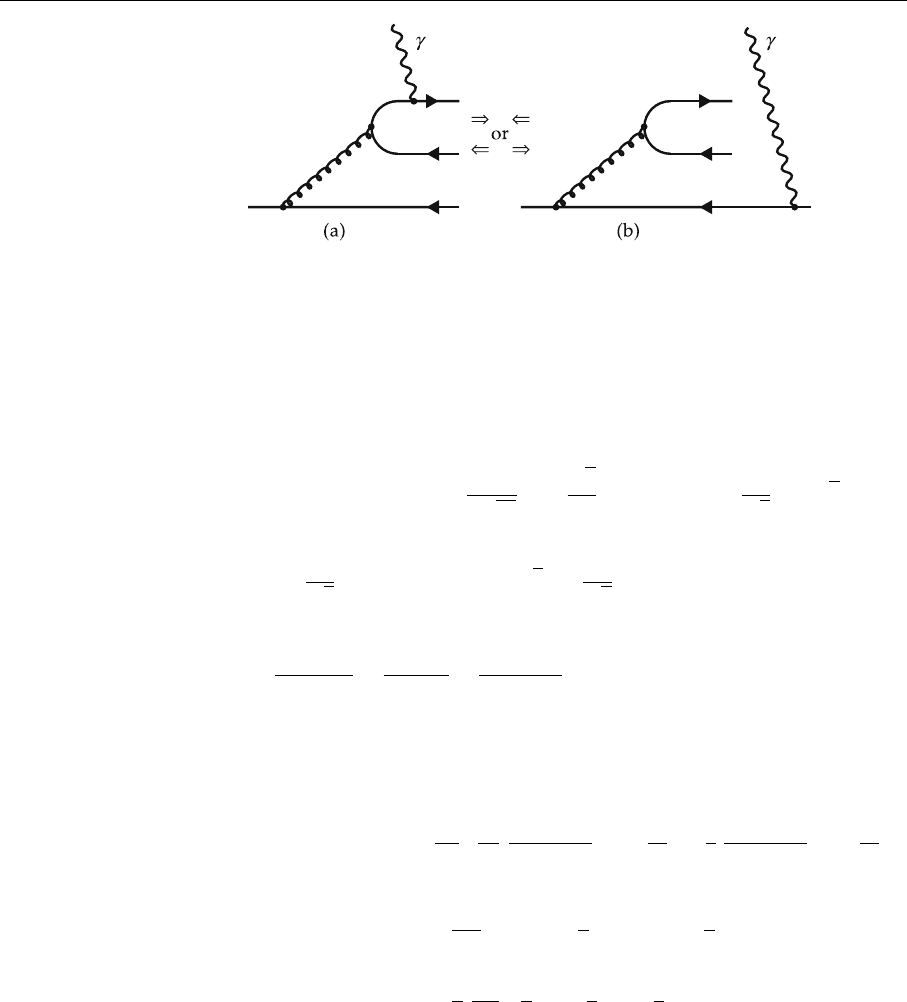
364 5. Perturbative QCD I: Deep Inelastic Scattering
Fig. 5.30. Graphs contribut-
ing to the Q
2
dependence
of the zeroth moment of
the unpolarized structure
functions. For the spin-
dependent structure func-
tions only (b) contributes,
since the quark–antiquark
pairs produced are unpolar-
ized
to measure F/D. However, the combined analysis of all the hyperon decays de-
scribed by different groups gave conflicting results. A conservative estimate is
F/D =0.55–0.60. From (5.310) we read off
∆u −∆d = F +D . (5.311)
Similarly by inserting the SU(3) isoscalar factors we get
,
N
S
5
8σ
N
= c ·n
σ
−
1
4
√
10
A
1
+
√
2
8
A
2
=c ·n
σ
−
1
√
3
D +
√
3F
(5.312)
⇒
1
√
3
∆u +∆d −2∆s
=
√
3F −
1
√
3
D . (5.313)
Assuming again that ∆s = 0 we obtain another independent combination,
∆u +∆d
∆u −∆d
=
3F −D
F +D
=
3F/D −1
F/D +1
, (5.314)
which together with (5.309) allows us to determine
1
+
0
g
p
1
(x) dx.Acomplete
analysis along these lines gives
1
0
dxg
p
1
(x, Q
2
) =
g
A
g
V
1
18
3F/D +1
F/D +1
1 −
α
s
π
+
1
9
3F/D −1
F/D +1
1 −
α
s
π
+
M
2
Q
2
1
0
dxx
2
2
9
g
p
1
(x, Q
2
) +
4
3
g
p
2
(x, Q
2
)
−
4
9
1
Q
2
4
9
f
2u
+
1
9
f
2d
+
1
9
f
2s
≈ 0.172 ±0.009 for Q
2
=5GeV
2
. (5.315)
This is the Ellis–Jaffe sum rule. As mentioned several times already, its validity is
a matter of dispute. We have presented it here to illustrate the potential usefulness
of flavor SU(3) for the analysis of deep inelastic scattering cross sections.
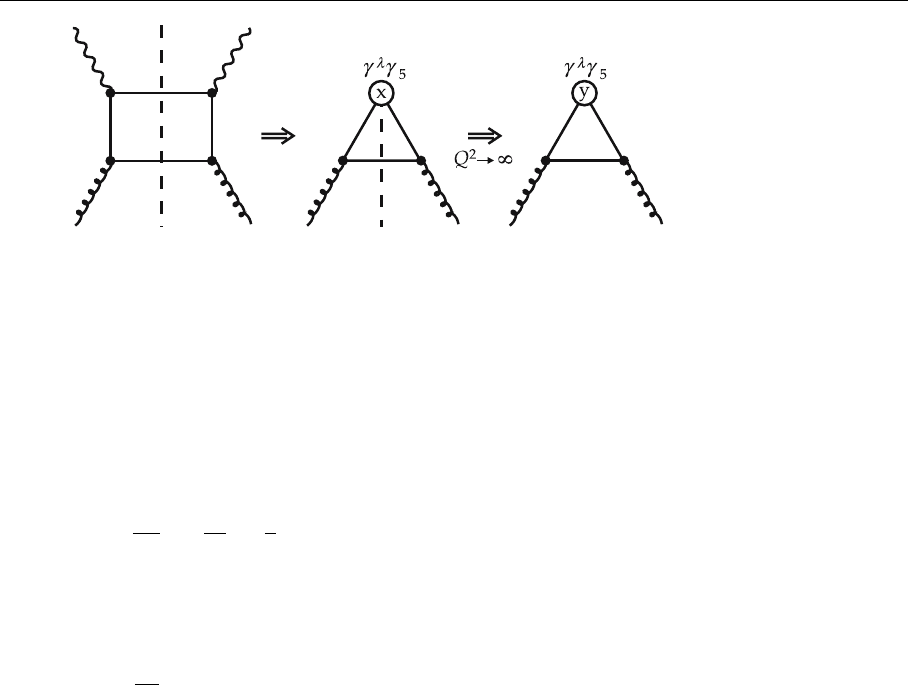
5.6 The Spin-Dependent Structure Functions 365
Fig. 5.31. The perturbative
anomalous gluon contribu-
tion to g
1
Next let us discuss the role of the anomaly for the isosinglet axial-vector
current. To illustrate the point consider first the perturbative graph in Fig. 5.31.
It is obvious that for Q
2
→∞one indeed obtains the triangle anomaly, im-
plying pointlike photon–gluon coupling. The basic problem of this interpretation
is also obvious from Fig. 5.29, namely that there is no unambiguous way to sepa-
rate the quark contribution and the anomalous gluonic contribution. It is unclear
whether the quarks of the fermion line should be absorbed into ∆u, ∆d,etc.or
into a contribution of the structure
∆g
p
1
(x) =
>
Q
2
q
2
?
1
0
dz
z
A
x
z
∆G(z). (5.316)
In other words, the ∆qs appearing in the analysis we have presented so far should
be split up according to
∆q = ∆
˜
q −
α
s
2π
∆G ·c . (5.317)
It turns out that, for variety reasons, such a separation is very problematic.
1. Performing the perturbative calculation for the graph in Fig. 5.29 we get con-
stants c that depend critically on the chosen infrared regulators indicating that
we are not looking at an infrared safe quantity.
2. From the operator-product-expansion point of view, we find that there is no
gauge-independent local definition of ∆G.
3. A so-called large gauge transformation, i.e., a gauge transformation with
a nonzero topological quantum number, shifts contributions from ∆
˜
q to ∆G.
A detailed discussion of this rather complicated issue is beyond the framework
of this book.
On the other hand, there exists a practical argument for the decomposition
(5.317). If we construct a phenomenological model for ∆q, we will most proba-
bly miss the highly virtual quark components from Fig. 5.29. Therefore it might
be easier to model ∆
˜
q and ∆G instead.
We will not discuss these still very much disputed questions further.

366 5. Perturbative QCD I: Deep Inelastic Scattering
EXAMPLE
5.16 Higher Twist in Deep Inelastic Scattering
In the framework of operator product expansion we found that structure func-
tions can be represented as
1
0
dxx
n−2
F(x, Q
2
) = C
n
(α
s
, Q
2
/µ
2
)V
n
(µ
2
) +O(1/Q
2
), (1)
where V
n
(µ
2
) are the reduced matrix elements of the twist-2 operators (see
(5.257)–(5.259)). The Wilson coefficients C
n
(α
s
, Q
2
/µ
2
) can be evaluated in
perturbation theory as an expansion in α
s
, which is actually an expansion in
1/ ln(Q
2
) because α
s
∼ 1/ ln(Q
2
).
We shall now discuss the (1/Q
2
) corrections that contribute to deep inelas-
tic scattering (DIS). This will be done in a quite heuristic way and, in order to
exemplify the main ideas, simple examples shall be used without going through
the operator product expansion, which would be necessary to obtain the (1/Q
2
)
corrections rigorously. The interested reader is referred to the literature and refer-
ences given there.
24
In general, power-suppressed contributions are referred to as
higher-twist contributions. This is, of course, a quite loose way of speaking. We
distinguish power corrections that are of pure kinematic origin, the so-called tar-
get mass corrections (TMC), which we have already discussed in Example 5.12,
and true higher-twist corrections. True higher-twist corrections are of dynami-
cal origin related to quark–gluon interactions in the nucleon. TMC consist of
power-suppressed twist-2 operators that occur in the expansion when the tar-
get mass is not set to zero, i.e. assumed to be negligible as compared to Q
2
.
Those corrections can be exactly taken into account by not expressing the struc-
ture functions in terms of the Bjorken variable x, but instead in terms of the
Nachtmann variable ξ:
25
ξ =
2x
1 +
1 +4x
2
M
2
N
Q
2
1/2
. (2)
Setting M
2
N
to zero, one recovers the normal Bjorken variable. The structure
functions expressed in terms of ξ depend analytically on M
2
N
/Q
2
and can be
expanded in that variable so that one recovers the 1/Q
2
corrections in the form
of (1). The classical papers of De Rujuly et al.
26
give some more insight into this
procedure. Here we will not dwell on this issue, but instead restrict ourselves to
24
B. Ehrnsperger et al.: Phys. Lett. B 150, 439 (1994).
25
O. Nachtmann: Nucl. Phys. B 63, 237 (1973).
26
A. De Rujula, W. Georgi, W.D. Politzer: Phys. Rev. D 15 (1997) 2495 and Ann. Phys.
(1997) 315.

5.6 The Spin-Dependent Structure Functions 367
the more interesting case of power suppressed twist-3 and twist-4 operators. The
rigorous definition of twist is
twist = dimension −spin , (3)
where dimension is the naive canonical dimension of the operator (see the fol-
lowing table), and spin relates to its transformation properties under the Lorentz
group. For example, the vector operator
ψγ
µ
ψ has spin 1, the scalar operator
ψψ has spin 0, etc. Using the fact that the action
+
d
4
xL = is dimensionless,
it is quite easy to derive the canonical dimensions of the field operators from
the knowledge of the Lagrangian. In the table we give the mass dimensions of
various operators.
operator P
µ
, D
µ
, A
µ
ψ G
µν
,
˜
G
µν
ψγ
µ
ψ L
dimension 0 1 3/22 34
How the decomposition of an operator into its irreducible representation un-
der the Lorentz group (well-defined spin) is done will be demonstrated by the
simple example of
ψiD
µ
γ
ν
ψ. It has two vector indices, i.e. it is the direct prod-
uct of two vectors, that means the maximal spin is 2. According to our knowledge
from coupling of angular momentum with Clebsch–Gordan coefficients
27
we
know that we can decompose it into a spin-0, a spin-1 and a spin-2 part. We can
write
ψi
ˆ
D
µ
γ
ν
ψ =
1
2
ψi
ˆ
D
µ
γ
ν
ψ +ψγ
µ
i
ˆ
D
ν
ψ
−
g
µν
4
ψ D/ψ
7
89 :
twist−2
+
1
2
ψi
ˆ
D
µ
γ
ν
ψ −ψγ
µ
i
ˆ
D
ν
ψ
7
89 :
twist−3
+
g
µν
4
ψ
ˆ
D/ψ
7
89 :
twist−4
, (4)
where the first line on the right-hand-side gives the twist-2, the second line
the twist-3, and the third line the twist-4 contribution. Since the operator is of
dimension-4 this corresponds to a spin-2, spin-1 and spin-0 contribution. The
spin-2 part is completely symmetric and traceless, the spin-0 part is the trace we
subtracted, and the remaining antisymmetric part has spin-1. In principle, such
a decomposition is possible for even higher operators but becomes increasingly
tedious and is not even unique, i.e. three spin-1 operators can be coupled to spin-
2 in two different ways. In (4) we have found one twist-2 operator, one twist-3
27
W. Greiner and B. Müller: Quantum Mechanics – Symmetries, 2nd ed., (Springer,
Berlin, Heidelberg 1994).
Example 5.16
