Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

328 5. Perturbative QCD I: Deep Inelastic Scattering

5.5 Calculation of the Wilson Coefﬁcients

In the previous section we recapitulated how the operator product expansion

separates scales, thus allowing us to describe moments of structure func-

tions through coefﬁcient functions calculable in perturbation theory and to

parametrize the nonperturbative contributions in terms of matrix elements of

operators of well-deﬁned twist.

These matrix elements then can be further investigated with nonperturbative

techniques such as lattice QCD, QCD sum rules, or models like the MIT bag

model. The Q

dependence of the Wilson coefﬁcient in addition can be stud-

ied with the help of the renormalization group equation; cf (5.180). There we

have shown how the Q

dependence of coefﬁcients is described at leading order.

To obtain the Q

dependence in next-to-leading order, we need the α

correc-

tions to the coefﬁcient functions. Therefore, in this section some techniques for

calculating Wilson coefﬁcients in perturbation theory are explained.

The key observation is that the coefﬁcient functions

,µ

) are indepen-

dent of the states for which we are calculating the time-ordered product:

PS|i

x e

iqx



(x)

(0)



|PS 





,µ

)PS|

(µ

)|PS 



µν

; (5.248)

cf (5.219). Hence we have the liberty to take which ever state is the simplest

and, of course, we choose quark and gluon states. Calculation of the time-

ordered product quark/gluon|i

x e

iqx



(x)

(0)



|quark/gluon  and

of the matrix elements quark/gluon|

(µ

)|quark/gluon  will give us the

answer for

,µ

We shall examplify the idea by investigating unpolarized Compton forward

scattering.

Let us write down the parametrization of the unpolarized part, which accord-

ing to (3.18) and (3.43) is given by

µν

( p, q) = i

x e

iqx

p, quark|T



(x)

(0)



|p, quark 



−g

µν



p ·q



−

p ·q



−

p ·q



. (5.249)

Here the superscript qq refers to the fact that we are considering quarks as

ingoing and outgoing hadronic states.

It is convenient to express the time-ordered product (5.249) in terms of the

structure functions

−2x

and

instead of

and

, which yields

5.5 Calculation of the Wilson Coefﬁcients 329

the decomposition

µν

( p, q) = e

µν

(x, Q

) +d

µν

(x, Q

) (5.250)

with

µν



µν

−



(5.251a)

and

µν



−g

µν

+ p

−( p

+ p

)



. (5.251b)

Using the projectors p

and g

µν

, we ﬁnd, for massless states p

=0,

( p ·q)

µν



( p ·q)

−

µν



µν

=−

−

µν

. (5.252)

To set the stage, we calculate the 4-point Green function in zeroth-order per-

turbation theory, i.e. the forward scattering amplitude of a virtual photon on

a quark target. The Feynman diagram is the same as we had in Fig. 5.18, only

now the nucleon states are replaced by quark states (Fig. 5.20).

We can immediately denote the amplitude as

qq(0)

µν



u(p, s)γ

p/ +q/

u(p, s)

u(p, s)γ

p/ −q/

u(p, s)

. (5.253)

The superscript (0) to T

qq(0)

µν

indicates the zeroth-order approximation in α

for

µν

. Note that there is an overall factor of i because we are computing i times

the time-ordered product in (5.219) or (5.249).

qqq

pppp

p+q p-q

Fig. 5.20.

Compton forward scattering

amplitude for photon–quark

scattering

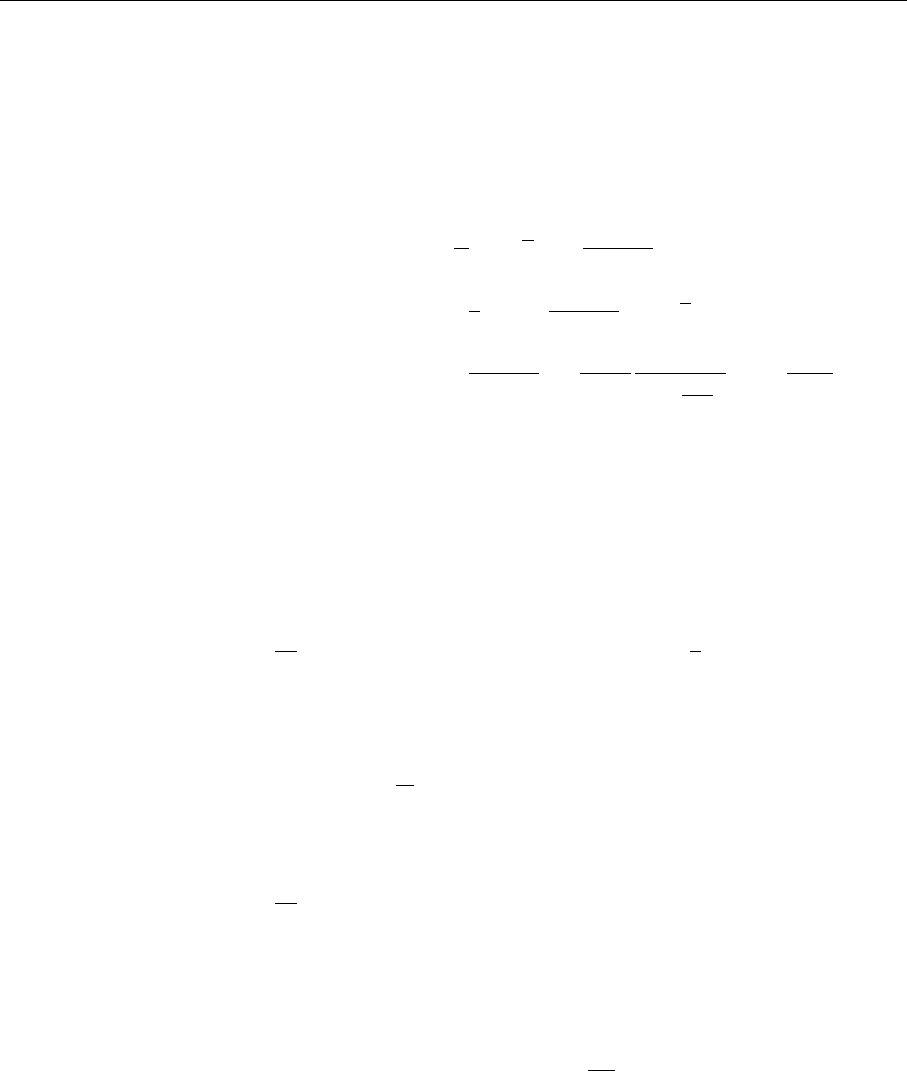
330 5. Perturbative QCD I: Deep Inelastic Scattering

The crossed diagram (second term) can be obtained by the replacement

µ ↔ ν, q →−q from the direct (ﬁrst) term. Hence it is sufﬁcient to concentrate

on the ﬁrst term.

Applying the projector (5.251a) onto

we ﬁnd immediatly

=0in

zeroth-order perturbation theory due to the equations of motions p/u( p, s) = 0.

This is a simple reﬂection of the celebrated Callan–Gross relation

= 2x

Turning to

we project with g

µν

and ﬁnd, for the direct term with γ

−2γ

µν

(direct) =−2





u(p, s)

p/ +q/

( p +q)

u(p, s)



(5.254)

=−2i





p/ +q/

( p +q)

u(p, s)u( p, s)



=−i

( p ·q)

( p +q)

= 2

( p ·q)



1 +

2p·q



=−ω

1 −ω

Remember, ω ≡ 1/x = 2p ·q/Q

=−2p ·q/q

. Expanding the denominator

gives

µν

(direct) =−2ω

∞



n=0

. (5.255)

Utilizing the second equation (5.252) with

= 0 and taking into account the

exchange term we ﬁnd, for

∞



n=0

n+1

+(−ω)

n+1

= 2



n=2,4

,ω=

, (5.256)

which is essentially the same expression as in (5.243), where we calculated

The only difference is the lack of the reduced matrix elements A

simply because

those are normalized to one for free quark states:

n−1

p, quark|

Ψγ

···

Ψ |p, quark =p

···p

. (5.257)

Had we done a similar calculation as previously we would have ended up

with



n=2,4

, (5.258)

where V

are the reduced matrix elements of the vector operator (5.257) in an

arbitrary state. Furthermore, by using dispersion relations as in the case of

we ﬁnally would ﬁnd the corresponding equation to (5.246) and (5.247):

dxx

n−2

(x, Q

) = C





(µ

), (5.259)

which shows that the nth power of ω is directly related to the nth moment of F

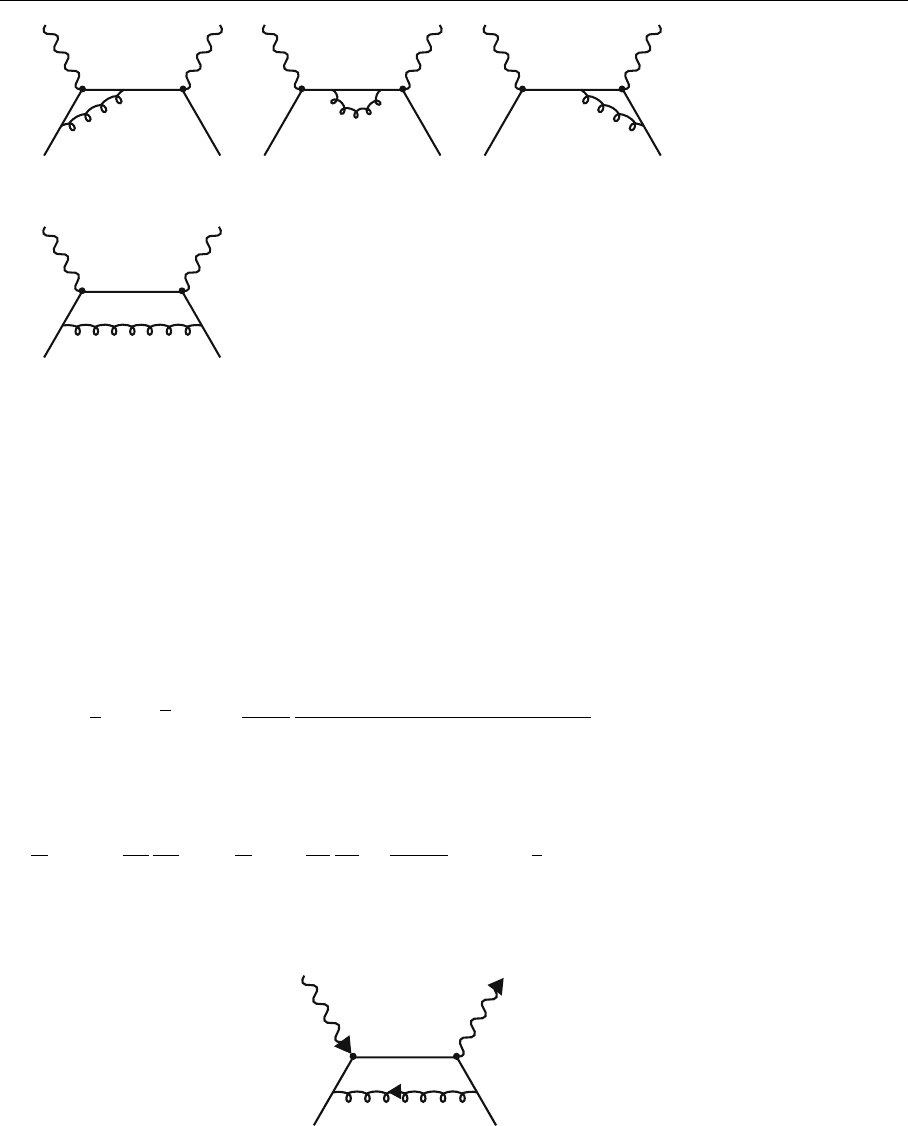
5.5 Calculation of the Wilson Coefﬁcients 331

+ exchange terms

Fig. 5.21. Order α

correc-

tion to the Compton for-

ward scattering amplitude

for photon–quark scattering

Keeping that in mind we proceed to our actual task, which is to calculate the

Wilson coefﬁcients at next-to-leading order, i.e. the order of α

corrections to the

forward scattering. The corresponding diagrams are depicted in Fig. 5.21.

We restrict ourselves to the calculation of C

(α

)), i.e. the Wilson coef-

ﬁcients for the longitudinal structure function, which measures the violation of

the Callan–Gross relation. The calculation of C

(α

)) involves only the last

diagram in Fig. 5.21, since all the others vanish by the equations of motion when

we project with p

Using the Feynman rules for the ﬁrst-order correction for the direct term in

Fig. 5.22 we ﬁnd

qq(1)

µν

(direct)

=iC



u(p, s)

(2π)

( p/ +k/)γ

( p/ +k/ +q/)γ

( p/ +k/)γ

( p +k)

( p +k +q)

u(p, s),

(5.260)

where we have already performed the color sum



A,a



b,i



−1

(5.261)

stemming from the Gell-Mann matrices entering at the quark gluon vertices.

+ exchange terms

p+k

p-k

p+k+q

Fig. 5.22. Diagram that con-

tributes to the O(α

) cor-

rection to the longitudinal

structure function F

(non-

singlet)

332 5. Perturbative QCD I: Deep Inelastic Scattering

In general we have to perform the calculation in d = 4 +2ε dimensions to

regularize divergencies. However, it turns out that for the projection onto F

the

integral is free of any divergence, which is not the case if we were to project with

µν

onto F

Performing the projection and using p

=0 we obtain

µν

(direct) = iC



(2π)

u(p, s)γ

k/ p/(k/ +q/) p/k/γ

u(p, s)

( p +k)

( p +k +q)

=−iC

(2π)

[

k/ p/(k/ +q/) p/k/ p/

]

( p +k)

( p +k +q)

, (5.262)

where we used



u(p, s)

Mu(p, s) = tr[

Mp/]and γ

p/γ

=−2p/. The trace can

be further simpliﬁed by again using p

= 0:

[

k/ p/(k/ +q/) p/k/ p/

]

=2kptr

[

k/ p/(k/ +q/) p/

]

=(2kp)

[

(k/ +q/) p/

]

=16



(k · p)

+(k · p)

( p ·q)



. (5.263)

What remains is therefore to perform the following integral:

µν

(direct)

=−16iC

(2π)

(k · p)

+(k · p)

( p ·q)

( p +k)

( p +k +q)

=−16iC



αβ

( p, q) p



+( p ·q)I

αβ

( p, q) p



. (5.264)

This will be achieved by using the Feynman parameter technique (4.95). We

begin with the integral

αβ

( p, q) =

(2π)

( p +k)

( p +k +q)

Γ(4)

Γ(2)Γ(1)Γ(1)

dvu

(2π)



( p +k)

u +( p +k +q)

v +k

(1 −u −v)



(5.265)

where we used the Feynman parametrization (see Exercise 4.7) and denote

u =

1 −u,

v =1 −v. The denominator can be simpliﬁed:



u(p +k)

+v( p +k +q)

(1 −u −v)



= k

(1 −u −v +u +v) +2k(up+v( p +q)) +( p +q)

= k

+2k(up+v( p +q)) +( p +q)

5.5 Calculation of the Wilson Coefﬁcients 333

=(k +up+v( p +q))

−(up+v( p +q))

+( p +q)



−2vupq+( p +q)



+vv



( p +q)

−

2pq





−vvQ



1 −

2pq(1 −u



)





−vvQ



1 −ω





with u



and k



= k +up+v( p +q) and therefore

k = k



−(u



v +v) p −vq . (5.266)

With that we get

αβ

( p, q) = Γ(4)

dvuv

(2π)







−vvQ

(1 −ωu)



(5.267)

where we have rewritten the integration

dvuf(u,v)=

duu f(u,v)=

dvv



f(u



v, v) .

(5.268)

The fact that the integral will be multiplied by p

again simpliﬁes our cal-

culation since due to the onshell condition p

=0weareallowedtoretainonly

the terms ∼ q

in the substitution k



αβ

( p, q) p

=Γ(4)( p ·q)

dvv

duu

(2π)



−vvQ

(1 −ωu)



. (5.269)

Similarly we get for the other integral in (5.264)

αβ

( p, q) p



=−Γ(4)( p ·q)

dvv

duu

(2π)



−vvQ

(1 −ωu)



(5.270)

334 5. Perturbative QCD I: Deep Inelastic Scattering

where the only difference is that instead of k

→k



→v

in (5.267)

we have k



→−q



. The remaining k integration is readily per-

formed with the help of the tables in (4.97) to (4.101):

(2π)



−vvQ

(1 −ωu)



(4π)

Γ(2)



vvQ

(1 −ωu)



Γ(4)

. (5.271)

Since we simpliﬁed the denominator in such an intelligent way that the

Feynman parameters factorize, we are now able to perform the

dv integration:

dvv

(vv)

−2

Γ(1)Γ(1)

Γ(2)

= 1 ,

dvv

(vv)

−2

Γ(1)Γ(2)

Γ(3)

. (5.272)

In passing, we note that the evaluation of the integrals within the Feynman

parameter integral is one of the main obstacles in multiloop calculations.

A factorization of Feynman parameters can always be enforced by expand-

ing nonfactorized expressions like (u +v)



n=0





a−n

for the price of

introducing an additional sum. Summarizing we get

qq(1)

µν

(direct) =

(4π)

( p ·q)

(1 −ωu)

. (5.273)

The superscript (1) to T

qq(1)

µν

indicates the ﬁrst order in α

approximation for T

µν

To perform the remaining u integration we expand the denominator

(1 −ωu)

∞



n=0

(n +1)(uω)

(5.274)

and with

duu

u =

Γ(n +1)Γ(2)

Γ(n +3)

(n +2)(n +1)

(5.275)

weendupwith

µν(1)

(direct) =

(4π)

( p ·q)

∞



n=0

(n +2)

4π

∞



n=0

n+1

(n +2)

. (5.276)

5.5 Calculation of the Wilson Coefﬁcients 335

The crossed diagram doubles even, and cancels odd, powers of ω so that we

ﬁnd

= 2C

4π



n=2,4,...

(n +1)

. (5.277)

The nth power of ω corresponds exactly to the nth moment of the structure

function F

as we saw in the introductory discussion. Indeed, comparing with

(5.256) to (5.259) leads us to the ﬁnal result

dxx

n−2

(x, Q

) = C

4π

(n +1)

dxx

n−2

(x, Q

). (5.278)

Now we want to express the above relation not only on the level of moments

of the structure function but also as a convolution in Bjorken-x space. With

dzz

n−1

z =

n +1

(5.279)

we can write

dxx

n−1

(x, Q

) = 4C

4π

dzz

n−1

dyy

n−1

( y, Q

)

=4C

4π

dz(zy)

n−1

( y, Q

)

=4C

4π

dxx

n−1





( y, Q

)

=4C

4π

dxx

n−1





( y, Q

) (5.280)

and therefore

(x, Q

) = 4C

4π





( y, Q

). (5.281)

So far we have only considered the O(α

) correction coming from photon–

quark scattering. However, to O(α

) also diagrams from photon–gluon scattering

containing a quark loop contribute (see Fig. 5.23).

336 5. Perturbative QCD I: Deep Inelastic Scattering

+ exchange terms

Fig. 5.23. O(α

) contribu-

tion to the Compton forward

scattering amplitude stem-

ming from photon–gluon

scattering

We will calculate those diagrams that contribute only to singlet structure

functions in Excercise 5.13. The ﬁnal result is

(x, Q

) = T



4π







1 −



( y), (5.282)

where T

is the color factor times a factor N

coming from the sum over

the quark ﬂavors running through the quark loop.

For F

we therefore have calculated the complete O(α

) corrections. As can

be seen from (5.280) and (5.282) F

is expressed in terms of the structure func-

tion F

(x, Q

) times a factor that is calculable in perturbation theory. F

(x, Q

)

is simply the quark distribution function F

(x, Q

) = xq(x, Q

) and the gluon

distribution function F

(x, Q

) = xG(x, Q

), respectively.

That F

is completely expressed through F

is due to the fact that only one

set of unpolarized operators V

(µ

) contributes to F

and F

– see (5.175) and

(5.176). (One has to keep in mind that the vector operators V

(µ

) contribute

to the unpolarized structure functions while the axialvector operators A

(µ

)

contribute to the polarized structure functions.)

We can therefore express F

and F

dxx

n−2

(x, Q

) = C

n,L





(µ

dxx

n−2

(x, Q

) = C

n,2





(µ

), (5.283)

and solving the equations for F

and F

by eliminating V

(µ

) we ﬁnd

dxx

n−1

(x, Q

) =

n,L





n,2





dxx

n−1

(x, Q

)

5.5 Calculation of the Wilson Coefﬁcients 337



m=1

(m)

n,L



4π



dxx

n−1

(x, Q

)



1 +



m=1

(m)

n,2



4π





dxx

n−1

(x, Q

)

n,L

4π



(2)

n,L

−C

(1)

n,L

(1)

n,2



4π







4π



&

dxx

n−1

(x, Q

). (5.284)

Here we have written the Wilson coefﬁcients as an expansion in α

/4π and

made use of the fact that F

is equal to zero at zeroth order and that usually

the corresponding coefﬁcient is normalized to 1 for F

. This means C

(0)

n,L

= 0

and C

(0)

n,2

= 1. With this we have shown that to all orders in α

, F

is determined

completely by F

up to higher-twist





corrections.

The expansion coefﬁcients C

(m)

n,2

corresponding to F

can be calculated in

a similar way as we did for F

. The calculations, however, are more lengthy

because now all diagrams of Fig. 5.21 contribute. An additional complication

arises due to the fact that the calculations have to be carried through in d dimen-

sions since for the projection onto F

the diagrams do not remain ﬁnite and have

to be renormalized.

The details of such calculations can be found in the very comprehensive pa-

per by Bardeen et al.

The coefﬁcient functions are available in the literature

for the ﬁrst 10 moments up to the third order.

The coefﬁcient functions for all

moments i.e. the full x dependence are available up to the second order.

Such

calculations cannot be done in the simple way presented here for the lowest order

but depend heavily on the use of algebraic computer codes. Also it seems not

to be feasible to push the calculations to even higher orders since at each order

the number of contributing diagrams increases considerably and with each ad-

ditional loop integration the necessary CPU time increases as well. Instead, the

study of the perturbative series to all orders in certain approximations will be per-

sued,e.g.forsmalln (n characterizes the nth moment of the structure function)

or for large N

W.A. Bardeen, A.J. Buras, D.W. Duke and T. Muta: Phys. Rev. D 18, 3998 (1978).

S.A. Larin, P. Nogueira, T. van Ritbergen and J.A.M. Vermaseren: Nucl. Phys. B

492,338 (1997).

E.B. Zijlstra and W.L. van Neerven: Nucl. Phys. B 383, 525 (1992).