Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

308 5. Perturbative QCD I: Deep Inelastic Scattering

EXERCISE

5.11 The Lowest-Order Terms of the β Function

Problem. Show that (5) in Example 4.3 or (4.156) indeed yields the lowest-

order contribution to the β function:

(−q

) =

(µ

)

1 +

11−2N

(−q

)/3

4π

(µ

) ln



−



. (1)

Here µ

denotes the renormalization point where α

(−q

) assumes the renor-

malized value α

(µ

). N

(−q

) is the number of light quarks with masses

smaller than −q

Solution. Equation (1) yields for g(−q

)

g(−q

) =

g(µ

)

1 +

11−2N

(−q

)/3

(4π)

(µ

) ln



−



(2)

with α

= g

/4π. We multiply (2) by the demominator on the right-hand side

and differentiate the resulting equation with respect to µ



(µ

) = g(−q

)

∂

∂µ

1 +

11 −

(−q

)

(4π)

(µ

) ln



−



= g(−q

)

11−2N

(−q

)/3

(4π)

1 +

11−2N

(−q

)/3

(4π)

(µ

) ln



−





2g(µ



(µ

) ln



−



−

(µ

)



. (3)

Once more we insert (2), into this expression and collect the terms containing g



(µ

)

1 +

11 −

(−q

)

(4π)

(µ

) ln



−



(

11 −

(−q

)

(4π)



(µ



(µ

) ln



−



−

(µ

)

2µ



, (4)



(µ

) =−

2µ

11 −

(−q

)

(4π)

(µ

). (5)

By means of (5) the β function now assumes the form

β = µ

∂g(µ)

∂µ

= 2µ

∂g(µ

)

∂µ

=−



11 −

(−q

)



(µ

)

(4π)

. (6)

5.4 Renormalization and the Expansion Into Local Operators 309

In fact this is identical with the ﬁrst term in (5.182). We can see immediately

where the higher terms come from. From Example 4.3, (1) is derived from vac-

uum polarization graphs. Consequently we obtain the higher-order contributions

to the β function if higher graphs are taken into account in this calculation.

Finally, we summarize the basic ideas of this last calculation. The renormal-

ization is carried out for a given value µ

of the momentum transfer, i.e., all

divergencies are subtracted in that renormalization scheme by relating to the

measured value of the coupling constant at the point, i.e. to α

(µ

).Thispro-

cedure yields a renormalized coupling constant α

(µ

) which has to be identiﬁed

with the physical coupling constant. However, we must decide on what we mean

by “physical QCD coupling” and then we must express the effective (running)

coupling α

) in terms of it. In QED the effective coupling is expressed in

terms of the ﬁne structure constant α ∼ 1/137 which is deﬁned as the effective

coupling in the limit −q

→0. In QCD α

(−q

) diverges as −q

→0. Hence

we cannot deﬁne α

(−q

) in terms of its value at −q

= 0. Instead we choose

some value of −q

,say−q

=µ

, and deﬁne the experimental QCD coupling

to be α

≡ α

(µ

).Therenormalization point µ

is, of course, arbitrary. Had we

instead chosen the point

then the two couplings would be related by

(µ

) =

(µ

)

1 +



11−2N

4π







Obviously (5.180) yields a restriction for

(n)

i,

, from which one can derive, using

(5.175) and (5.176), a constraint for the observable structure functions. In this

way our formal analysis leads to measurable predictions. Equations of the type

(5.180) are called renormalization group equations or Callan–Symanzik equa-

tions. They play an important role in formal considerations of ﬁeld theories,

because they yield nonperturbative results.

We now wish to explain the meaning of the β function in some more de-

tail. As shown in Exercise 5.11, the coupling constant g in fact depends on the

dimensionless quantity t =+

ln Q

/µ

. This enables us to write the deﬁning

equation of the dimensionless β function as

β = µ

∂g(µ)

∂µ

=µ

∂t

∂µ

∂g(t)

∂t

=−

∂g(t)

∂t

. (5.183)

The β function describes how the coupling depends on the momentum transfer,

given a ﬁxed renormalization point µ

. In fact there are two deﬁnitions known

in the literature. The ﬁrst one is expression (5.183) and the second one is

β(g) =t

∂g(t)

∂t

= Q

∂g(Q

)

∂Q

. (5.184)

A great advantage of the latter deﬁnition is that its features are not dependent

on the sign of t and they can be analyzed in a more general manner. Because of

Exercise 5.11

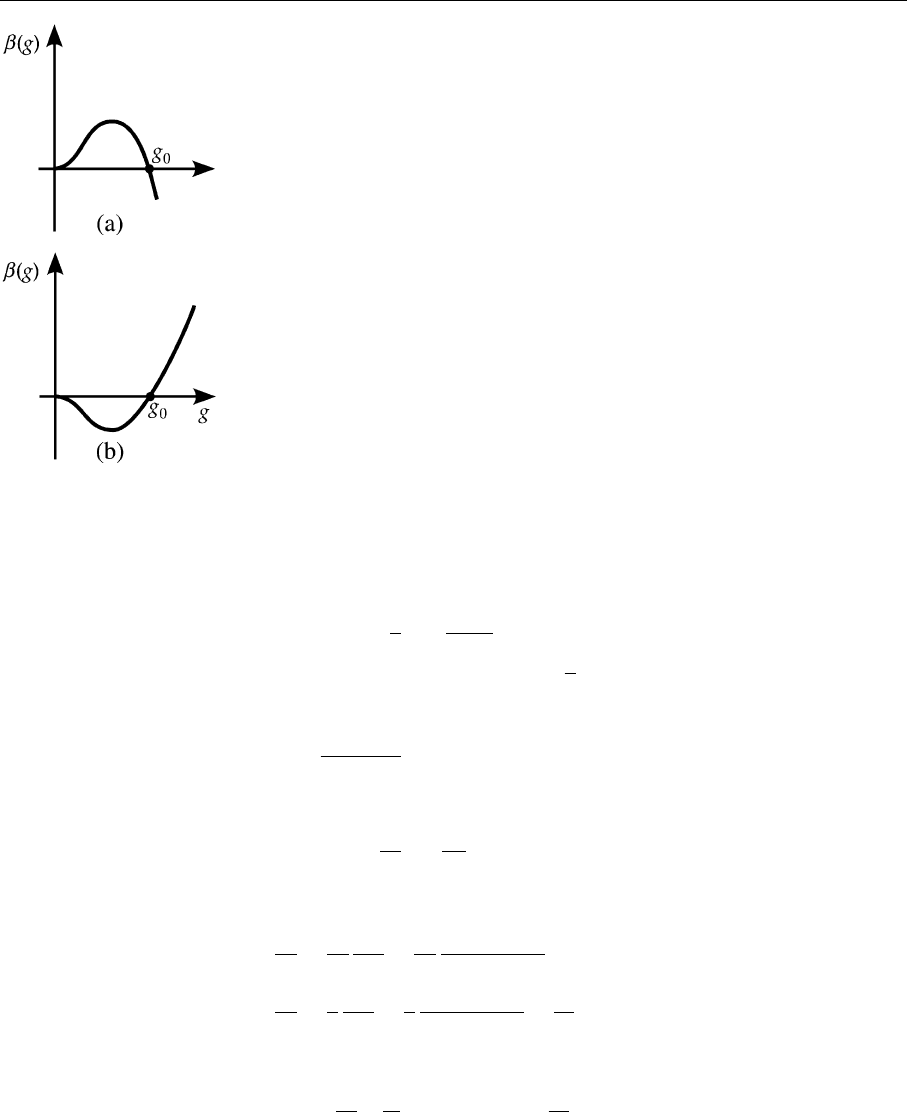
310 5. Perturbative QCD I: Deep Inelastic Scattering

Fig. 5.14a,b. The behaviour

of the β function as a func-

tion of the running coup-

ling constant g.The arrows

attached to the curve indi-

cate the direction of move-

ment along g(Q

) when

→∞

these two different deﬁnitions, the renormalization group equations found in the

literature sometimes differ by a factor t in front of the β function.

The zeros of the β function are crucial for the general behavior of the coupling

constant in the case of very large momentum transfers (the so-called ultravio-

let limit) and very small momentum transfers (the so-called infrared limit)and

thus for the most basic properties of the theory. This can be easily understood by

analyzing the two examples in Fig. 5.14.

Case (a) If β(g) is positive, then g becomes larger with increasing Q

.In

the region g < g

, g therefore approaches the value g

with increasing Q

.On

the other hand β(g) is negative for g > g

and here g becomes smaller with

increasing Q

. g

is therefore called a stable ultraviolet ﬁxpoint. This point,

however, is not stable in the infrared limit. As soon as g is different from g

and consequently

β(g) no longer vanishes, g moves away from the value g

for

decreasing Q

. Correspondingly the behavior at the point g = 0 is just the op-

posite. This is a stable infrared ﬁxpoint and it is unstable in the ultraviolet limit.

Hence Fig. 5.12a characterizes a theory whose coupling constant vanishes for

small momentum transfers and assumes a constant value for large momentum

transfers.

Case (b) In this case the points g = 0andg = g

have exchanged their mean-

ings compared to Case (a). The coupling constant vanishes for large momentum

transfers. This behavior is called asymptotic freedom. For small momentum

transfers g assumes the constant value g

.Ifg

is very large, which is known as

infrared slavery, such a theory exhibits similar features to QCD. For our problem

we want to evaluate (5.180) using perturbation theory. To this end we use

β =−



11 −



(4π)

=−bg

(5.185)

as an approximation for β(g). With

g we now denote the running coupling

constant as the solution of (5.185). Combining (5.183) with (5.185) we ﬁnd

1 +2bg

, (5.186)

and (5.180) becomes







−bg

∂

∂g

+µ

∂

∂µ



j

+γ

(n)

j



(n)

i,

, g,µ)= 0 . (5.187)

Furthermore it holds that

∂

∂t

∂

∂t

−g

2bg

(1 +2bg

=−b

, (5.188)

∂

∂g

∂

∂g

(1 +2bg

, (5.189)

and hence the derivatives in (5.187) acting on

g yield zero:



−bg

∂

∂g

−

∂

∂t



g(g, t) =−bg

= 0 . (5.190)

5.4 Renormalization and the Expansion Into Local Operators 311

The solution of (5.187) for γ

(n)

i, j

= 0 is therefore simply

(n)

i,

, g,µ)= f

i,

(

g(g, t)) , (5.191)

with an unknown function f

i,

(

g(g, t)). Thus the renormalization group equation

implies that, when γ

(n)

i, j

=0, the entire Q

dependence arises from the running

of the coupling constant g(g, t) which in turn is governed by (5.181). Therefore,

if we replace g by the running g(t) we ﬁnd with the help of (5.188) that (5.187)

can be transformed into a total derivative



−b

∂

∂g

+µ

∂

∂µ



∂

∂t

∂

∂g

∂

∂t

, (5.192)

so that the differential equation







j

+γ

(n)

j



(n)

i,

(g(g, t)) = 0 (5.193)

can be easily integrated to give

(n)

i,

, g,µ)=



i,k



g(g, t)



exp

⎡

⎣

−



(n)

k,



g(g, t



)



⎤

⎦

. (5.194)

Now we also expand the γ

(n)

k,

into a power series

(n)

k,

(n)

k,

(n)

k,

g +d

(n)

k,

+··· . (5.195)

A perturbative calculation shows that both the constant and linear terms are equal

to zero. The lowest-order contribution is proportional to

. Hence the t



integral

can be approximately evaluated:

−



(n)

k,

≈−d

(n)

k,

1 +2bg



=−

(n)

k,

ln(1 +2bg

t), (5.196)

(n)

i,

(t, g) =



i,k



g(g, t)



(1 +2bg

−d

(n)

k,

/2b



i,k



g(g, t)



(g, t)/g



(n)

k,

/2b

. (5.197)

In the last step we used the deﬁnition of the running coupling in (5.186). In the

limiting case t  1,

g →0 the function f

i,k



g(g, t)



assumes a constant value

(n)

i,k

t  1 , x constant ⇒

(n)

i,

(t, g) =



(n)

i,k



(g, t)/g



(n)

k,

/2b

(5.198)

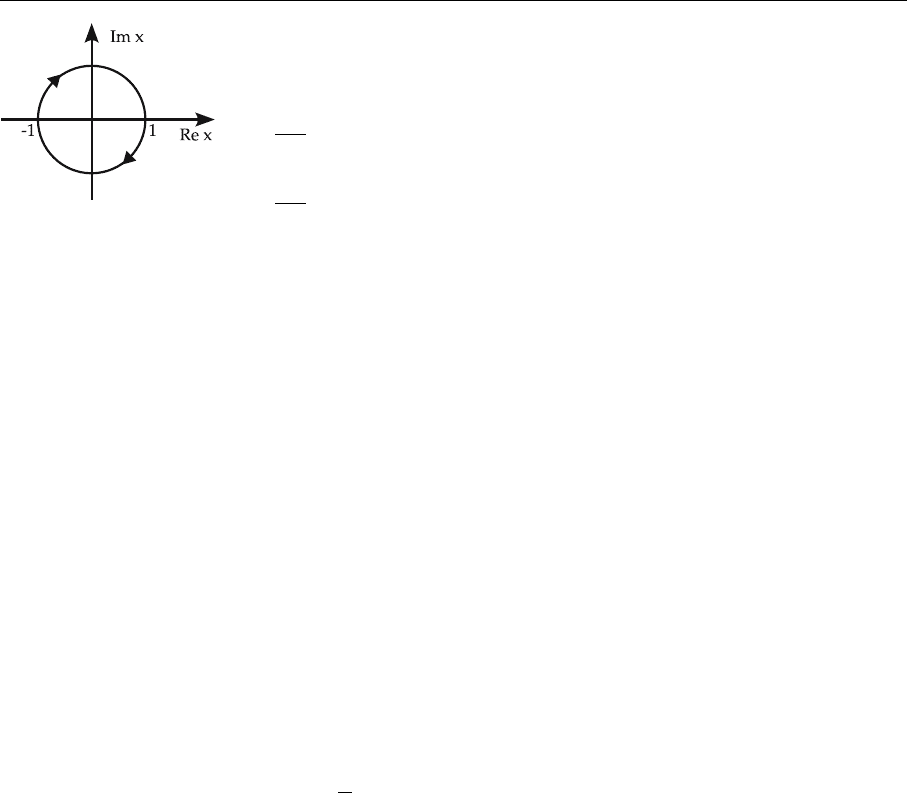
312 5. Perturbative QCD I: Deep Inelastic Scattering

Fig. 5.15. Integration con-

tour C in (5.199) and (5.200)

We insert this into (5.175) and (5.176), which we slightly modify for this

purpose. Let F

(z, Q

) be the complex continuation of F

(x, Q

).Thenwe

obviously have

2πi

(z, Q

n−1

dz = 2



(n)

1, j

(n), j

, (5.199)

2πi

(z, Q

n−2

dz = 4



(n)

2, j

(n), j

, (5.200)

with the integration contour C

depicted in Fig. 5.15. Since F

(z) and F

(z) can

become singular only in the case z → 0, C can be deformed and replaced by an

ε prescription:

(z, Q

n−1

dz =

−1

(x +iε, Q

n−1

−

−1

(x −iε, Q

n−1

−1



(x +iε, Q

) −F

∗

(x +iε, Q

)



n−1

dx .

(5.201)

Now we have to determine how the analytically continued structure function be-

haves under complex conjugation. Thus we have to take into account that W

µν

the imaginary part of the scattering amplitude in the forward direction T

µν

(this

is a special case of the so-called optical theorem):

µν



µν



. (5.202)

Correspondingly we have



x +iε, Q



−F

∗



x +iε, Q



= 2ImF



x, Q



, (5.203)



z, Q



n−1

dz = 4



x, Q



n−1

dx =: 4M

(n+1)





(5.204)



z, Q



n−2

dz = 4



x, Q



n−2

dx =: 4M

(n)





(5.205)

5.4 Renormalization and the Expansion Into Local Operators 313

This completes our derivation of (5.175) and (5.176) where the structure func-

tions were given as expansions in 1/x. Now we have suceeded in analytically

continuing them to the physical region 0 < x < 1. The quantities M

(n)

and M

(n)

are called moments of the structure functions. Owing to (5.198) they obey the

evolution equations

(n+1)

(t) =



(n)

1,k



(g, t)



(n)

/2b

(n), j

, (5.206)

(n)

(t) =



(n)

2,k



(g, t)



(n)

/2b

(n), j

. (5.207)

In fact these equations correspond to the GLAP equations. We shall prove this

for the nonsinglet contributions to the moments of the structure functions. Since

(n)

is diagonal for j = NS, the manipulations required are quite simple. The

moments of the NS-quark distribution functions are deﬁned as

(n+1)

1,ij

(t) =

n−1

∆

(x, t) dx . (5.208)

Equation (5.67) then yields (we substitute x = yz in the second step)

(n+1)

1,ij

(t) =

dxx

n−1

(t)

2π

∆

( y, t)P





(t)

2π

n−1

∆

( y, t)P





(t)

2π

dy∆

( y, t)y

n−1

dzP

n−1

(t)

2π

(n)

(n+1)

1,ij

, (5.209)

with

(n)

dzP

n−1

. (5.210)

From (5.206) it follows that

(n+1)

1,NS

(t) = M

(n+1)

1,NS



(g, t)



(n)

/2b

, (5.211)

314 5. Perturbative QCD I: Deep Inelastic Scattering

where M

(n+1)

1,NS

= M

(n+1)

1,NS

(t = 0) =



(n)

(n), j

is the moment of the struc-

ture function at the renormalization point µ

= Q

,i.e.t =

ln(Q

/µ

) = 0and

correspondingly g(t = 0) = g. We now differentiate this equation with respect

to t, so that we can compare it with (5.209), especially the coefﬁcients of both

equations, and ﬁnd a relation between the integral over the splitting function

(n)

(5.210) and the anomalous dimensions d

(n)

∂M

(n+1)

1,NS

(t)

∂t

(n)



−b



(n+1)

1,NS

(t)

=−

(n)

(n+1)

1,NS

(t) =

(t)

2π



−8π

(n)



(n+1)

1,NS

(t). (5.212)

Clearly (5.212) and (5.209) are the same relations, provided −8π

(n)

is iden-

tiﬁed with D

(n)

.Iftheγ

(n)

are evaluated by means of perturbation theory, we

obtain the expression (5.210) for d

(n)

with P

(z) given in Example 5.6.

Let us now reﬂect a little more on what we have learnt from the comparison

of the OPE approach to evolution of structure functions and the GLAP approach.

Equation (5.211) tells us how the QCD equations for the evolution of moments

look like. Dropping unnecessary labels we have for the nonsinglet case

(n)

(t) =

(t)

g(t = 0)

(

(n)

/2b

·M

(n)

(t = 0),

while for the singlet case one has

(n)

(t) =

(t)

g(t = 0)

(

(n)

/2b

·M

(n)

(t = 0),

where d

now is to be considered as a matrix





It only remains to calculate the anomalous dimensions d

(n)

and d

(n)

to predict the

moments of the structure functions at arbitrary t =

ln(Q

/µ

) from those given

at t = 0. In other words we obtain the moments at virtuality Q

if they are known

at the renormalization point Q

=µ

. While this approach is fairly rigorous and

not too difﬁcult to handle, it may lack physical interpretation and, in particular,

the connection to the simple parton model is not to fully apparent.

Taking the derivative on both sides of (5.211) with respect to t and comparing

with (5.209) we have immediatly found that (5.211) can be cast into the form of

the GLAP equations

∂∆

∂t

2π

∆

( y, t)P





, (5.213)

5.4 Renormalization and the Expansion Into Local Operators 315

whereweidentiﬁed

dzP

(z)z

n−1

=−8π

(n)

Thus the integral over the splitting function can be identiﬁed with the anomalous

dimension and (5.213) tells us how the structure function changes with t.Actu-

ally P

can be interpreted as governing the rate of change. However, this GLAP

equation is a complicated integrodifferential equation. Its transformation to mo-

mentum space reduces it to a set of ordinary differential equations that can be

easily solved.

EXAMPLE

5.12 The Moments of the Structure Functions

In this example we discuss the physical meaning of the moments of structure

functions. Looking at (5.175), (5.176), (5.203), (5.204), (5.208), and (5.209) one

could get the impression that knowing the structure function is equivalent to

knowledge of all its moments. But this is only true in the limit Q

→∞.For

every ﬁnite Q

, deviations occur owing to the corrections that were neglected on

the way from (5.142) to (5.143). One can prove that the corrections to

···µ

i.e., to C

(n)

and therefore to the nth moment of the structure function F

and to

the (n +1)th moment of F

, are suppressed by a factor

nµ

, (1)

where µ

is some mass scale. Equation (1) shows already that for every ﬁnite Q

the corrections become large at some value of n, i.e., each perturbative calcu-

lation of the moments is only valid up to a speciﬁc maximum number n.The

factor (1) can be understood quite easily. Equation (5.166) is inserted into the

expression for the scattering tensor and contracted with the leptonic scattering

tensor. Then we count how often terms of the kind

···q

···p

i−1

i+1

···p

j−1

j+1

···p

(2)

occur compared to the term

···q

···p

. (3)

This procedure yields the factor n.

Thus a perturbative QCD calculation is well

suited for the lower moments, for example, the integral over the structure func-

tions, but fails in the case of the higher moments. From (5.204) and (5.205) these

Since the explicit calculation is quite cumbersome, we refer to A. de Rujula,

H. Georgi, and H.D. Politzer: Ann. Phys. 103, 315 (1977)

316 5. Perturbative QCD I: Deep Inelastic Scattering

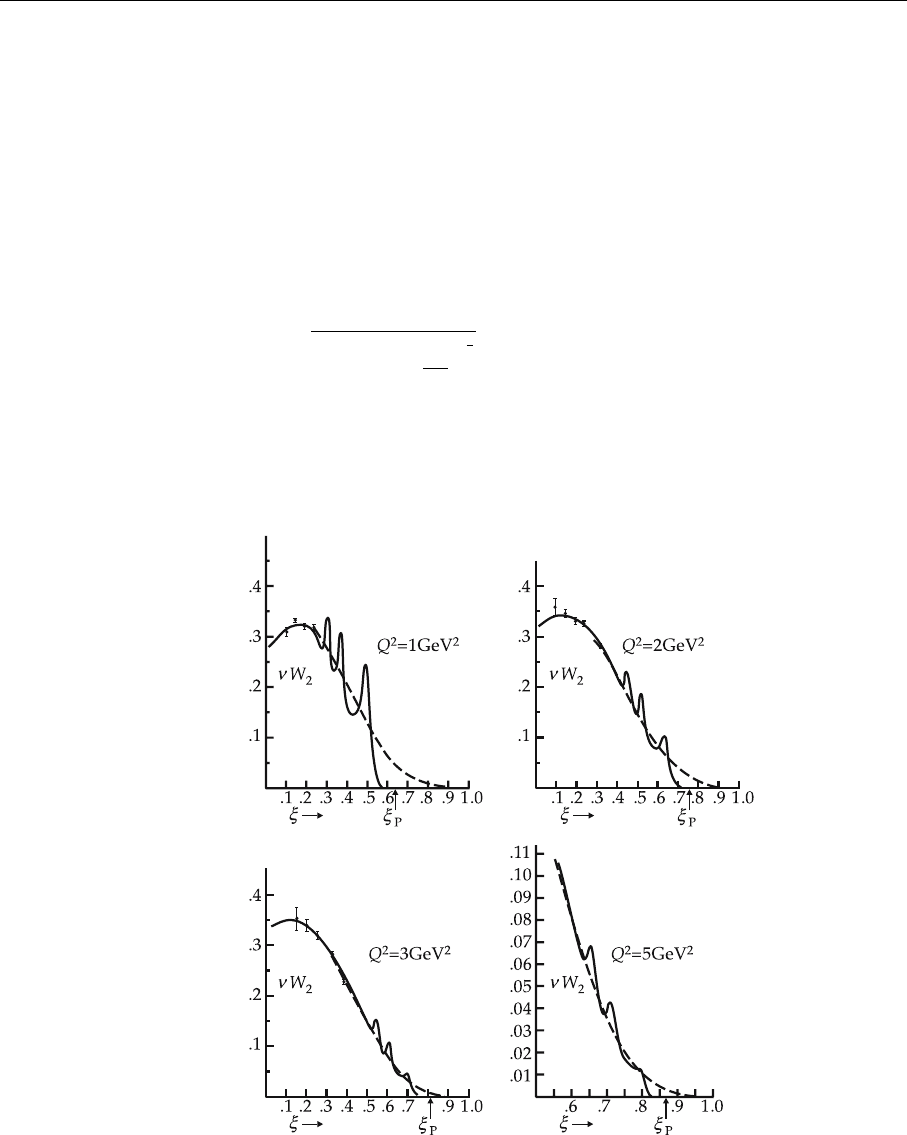
Example 5.12

Fig. 5.16. Comparison of

the experimental structure

function νW

for electron–

proton scattering with the

result of a perturbative QCD

calculation. ξ denotes the

Nachtmann variableand ξ

the position of the elastic

peak. From A. de Rujula,

H. Georgi, H.D. Politzer:

Ann. Phys. 103, 315 (1977)

higher moments are determined by the structure functions near x = 1. The value

x = 1, however, represents elastic scattering. Correspondingly here we ﬁnd the

elastic peak and for x slightly below 1 we ﬁnd peaks due to the different res-

onances. Since these resonance structures depend on the individual features of

the hadronic bound states, there is no way to describe this region by perturba-

tive QCD. On the other hand, this analysis clearly shows that the nonperturbative

effects must be included in higher-order terms of the operator product expansion.

The points just discussed (usually referred to as precocious scaling)are

explained again in Fig. 5.16. This ﬁgure depicts the experimentally observed

structure function νW

(x, Q

) (full line), which converges to F

(x) for large Q

The Nachtmann variable

ξ =

1 +



1 +4x



(4)

has been used instead of x. In the limit Q

→∞, ξ is equivalent to x. At ﬁnite Q

this variable takes the effects of the nucleon mass into account. The contributions

5.4 Renormalization and the Expansion Into Local Operators 317

of the various resonances can be clearly identiﬁed. The elastic peak at ξ

is not

plotted.

The dashed curve results from a perturbative QCD calculation. Clearly the

agreement becomes better for increasing Q

values, since here the effect of the

individual hadron resonances can be neglected. But also for small values of Q

the lowest moments

(1)

) =

(x, Q

) x

−1

dx (5)

and

(2)

) =

(x, Q

) dx (6)

are quite well described by the QCD calculation.

Before we continue our discussion of the OPE (operator product expansion)

we brieﬂy summarize the derivations carried out so far. Employing deep in-

elastic scattering as an example, we explained how scattering tensors can be

expanded into products of divergent coefﬁcient functions, which can be evalu-

ated by means of perturbation theory and ﬁnite matrix elements not dependent

on the momentum transfer, for example. In the case of F

(x, Q

) we had

dxx

n−2

(x, Q

) = 2πi



(n)

2, j



, g,µ



(n), j

. (5.214)

This so-called factorization into a Q

-dependent perturbative part and ﬁxed

numbers A

(n), j

that contain information about the distribution functions at

agivenvalueof Q

is of fundamental importance to most QCD applications.

We showed the possibility of factorization for deep inelastic scattering, but in

fact one must prove that this method is not destroyed by higher-order terms.

Since each soft (Q

is small of the order ∼ 1 GeV) gluon line couples strongly

(α

) is large), higher orders in QCD are in general as important as the lowest

order. Therefore the validity of the expansion (5.214), or of analogous expan-

sions for other processes, has to be investigated very carefully. Because of its

fundamental importance we shall discuss this question in the following section.

The nonperturbative matrix elements A

(n), j

can be treated as pure parameters or

can be calculated with help of nonperturbative models, e.g., the MIT bag model.

To clarify this statement we return to the starting point of our discussion, which

was the QCD analysis of the commutator of hadronic currents,



(x),

(0)



−

(5.215)

Example 5.12