Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


318 5. Perturbative QCD I: Deep Inelastic Scattering
which, taken between nucleon (spin
1
2
) particles, yields the hadronic scattering
tensor (see (5.1)):
1
2π
d
4
x e
iqx
PS|
ˆ
J
µ
(x),
ˆ
J
ν
(0)
−
|PS =W
µν
. (5.216)
Let us now formulate the basic ideas of the OPE by analysing the Compton
scattering amplitude
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
, (5.217)
which is related by virtue of the optical theorem (5.202) to the cross section:
1
π
Im
#
i
d
4
x e
iqx
PS|T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
|PS
&
=
1
2π
d
4
x e
iqx
PS|
ˆ
J
µ
(x),
ˆ
J
ν
(0)
−
|PS (5.218)
The basic idea of OPE now is to perform a separation of scales. Analysing deeply
inelastic scattering we have to deal with two separate scales. One is the limit of
high virtualities Q
2
→∞, pq →∞, the Bjorken limit, which can be identified
with physics on the light cone in coordinate space x
2
→0. According to the be-
havior of the running coupling, which vanishes at Q
2
→∞we may treat this
region of phase space using perturbative methods.
The other scale of typical hadronic size M
2
∼ 1GeV
2
comes about when we
analyze the current commutator between nucleon states.
The OPE separates these two scales:
i
d
4
x e
iqx
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
=i
d
4
x e
iqx
i
C
i
(x,µ
2
)
ˆ
O
i
(µ
2
)
µν
=
i
˜
C
i
(Q
2
,µ
2
)
ˆ
O
i
(µ
2
)
µν
. (5.219)
The coefficient functions
˜
C
i
(Q
2
,µ
2
) = i
+
d
4
x e
iqx
C
i
(x,µ
2
) (called Wilson co-
efficients) contain only virtualities that are larger than the separation scale µ
2
,
while the operators
ˆ
O
i
(µ
2
) contain only contributions from momenta smaller
than µ
2
(see Fig. 5.17).
Motivated by the behavior of the running coupling one now invokes the fol-
lowing assumption: The coefficient functions
˜
C
i
(Q
2
,µ
2
) are treated completely
perturbatively while the operators are assumed to be of nonperturbative nature.
That means that the coefficient functions obey usual renormalization group equa-
tions and can be systematically expanded in powers of α
s
(Q
2
,µ
2
), while the
matrix elements PS|
ˆ
O
i
(µ
2
)|PS in principle are unknown and parametrize our
ignorance of bound-state complexities. However, in some special cases, matrix
elements occuring in the analysis can be related to processes other than deep
inelastic scattering.
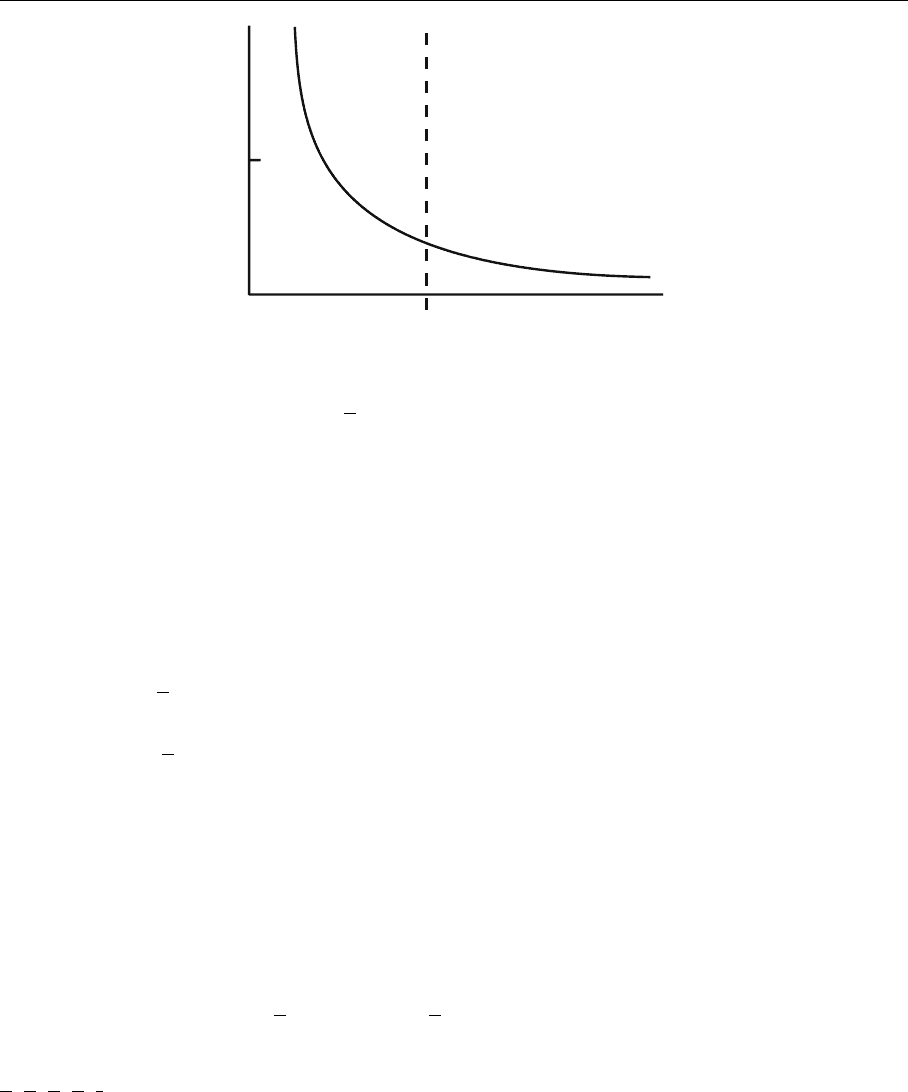
5.4 Renormalization and the Expansion Into Local Operators 319
α
s
(Q )
2
Q
2
1
m
2
Bjorken limit
quarks and gluons
hadronic
scale
bound states of
quarks and gluons
Fig. 5.17. Running QCD
couplingconstant as a func-
tion of the virtuality Q
2
.
High virtuality, Q
2
→∞,
corresponds to free quarks
and gluons. Q
2
< 1GeV is
the region where quarks and
gluons are bound to hadrons
For instance, the operator proton|
ˆ
Ψγ
µ
γ
5
ˆ
T
3
ˆ
Ψ |proton occurs in spin-
dependent deep inelastic scattering and can be related by isospin symmetry to
an operator occuring in weak β decay:
proton|
ˆ
Ψγ
µ
γ
5
ˆ
T
+
ˆ
Ψ |neutron . (5.220)
Let us now derive the separation of scales, i.e. the separation into perturbative
and nonperturbative contributions to the hadronic scattering tensor.
To be explicit we consider vector currents
ˆ
J
µ
(x) =
f
e
f
ˆ
Ψ
f
(x)γ
µ
ˆ
Ψ
f
(x),
ˆ
J
ν
(0) =
f
e
f
ˆ
Ψ
f
(0)γ
µ
ˆ
Ψ
f
(0), (5.221)
i.e. only purely electromagnetic interactions. The sum runs over the different
quark flavors: u, d, c, ... . Taking weak interactions into account imposes
no further difficulties, we only have to take care of additional axial vector
combinations.
13
These currents have to be inserted into (5.215) to (5.219). Equation (5.217)
then becomes
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
=
ff
T
e
f
ˆ
Ψ
f
(x)γ
µ
ˆ
Ψ
f
(x)e
f
ˆ
Ψ
f
(0)γ
µ
ˆ
Ψ
f
, (5.222)
13
See W. Greiner and B. Müller: Gauge Theory of Weak Interactions, 3rd ed. (Springer,
Berlin, Heidelberg 2000).

320 5. Perturbative QCD I: Deep Inelastic Scattering
which can further be simplified with Wick’s theorem
14
T
ˆ
Ψ
α
(x)
ˆ
Ψ
β
( y)
=−:
ˆ
Ψ
β
( y)
ˆ
Ψ
α
(x) :+0|T
ˆ
Ψ
α
(x)
ˆ
Ψ
β
( y)
|0 ,
(5.223)
where 0|T
ˆ
Ψ
α
(x)
ˆ
Ψ
β
( y)
|0 =iS
αβ
(x, y) is the usual Feynman propagator.
The free propagator can be written in the usual way:
iS(x, y) =
d
4
p
(2π)
4
e
iq(x−y)
i
p/ −m +iε
=
i
2π
2
(x/ −y/)
[(x −y)
2
−iε]
2
+O(m).
(5.224)
Applying (5.223) to (5.217) we thus obtain
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
=
ff
: e
f
ˆ
Ψ
f
(x)γ
µ
ˆ
Ψ
f
(x) ::e
f
ˆ
Ψ
f
(0)γ
ν
ˆ
Ψ
f
(0) :
+
f
e
2
f
ˆ
Ψ
f
(x)γ
µ
iS(x, 0)γ
ν
ˆ
Ψ
f
(0)
+
f
e
2
f
ˆ
Ψ
f
(0)γ
ν
iS(0, x)γ
µ
ˆ
Ψ
f
(x)
−
f
e
2
f
tr
$
γ
µ
iS(x, 0)γ
ν
iS(0, x)
%
. (5.225)
Inserting the free fermion propagator yields
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
=
f
e
2
f
tr
γ
µ
x/γ
ν
y/
·
1
4π
4
1
(x
2
−iε)
4
−
i
2π
2
e
2
f
ˆ
Ψ
f
(x)γ
µ
x/γ
ν
ˆ
Ψ
f
(0)
1
(x
2
−iε)
2
+
i
2π
2
e
2
f
ˆ
Ψ
f
(0)γ
ν
x/γ
µ
ˆ
Ψ
f
(x)
1
(x
2
−iε)
2
+
ff
: e
f
ˆ
Ψ
f
(x)γ
µ
ˆ
Ψ
f
(x) ::e
f
ˆ
Ψ
f
(0)γ
ν
ˆ
Ψ
f
(0) : .
(5.226)
If we sandwich the time-ordered product (5.222) between proton states
PS|T()|PS the process of deep inelastic scattering can be graphically
depicted (see Fig. 5.17).
OPE separates the free quark and gluon propagation from bound-state com-
plexities. While the upper part of the diagram may be treated with the tools of
14
See W. Greiner and J. Reinhardt: Field Quantization (Springer, Berlin, Heidelberg
1996).
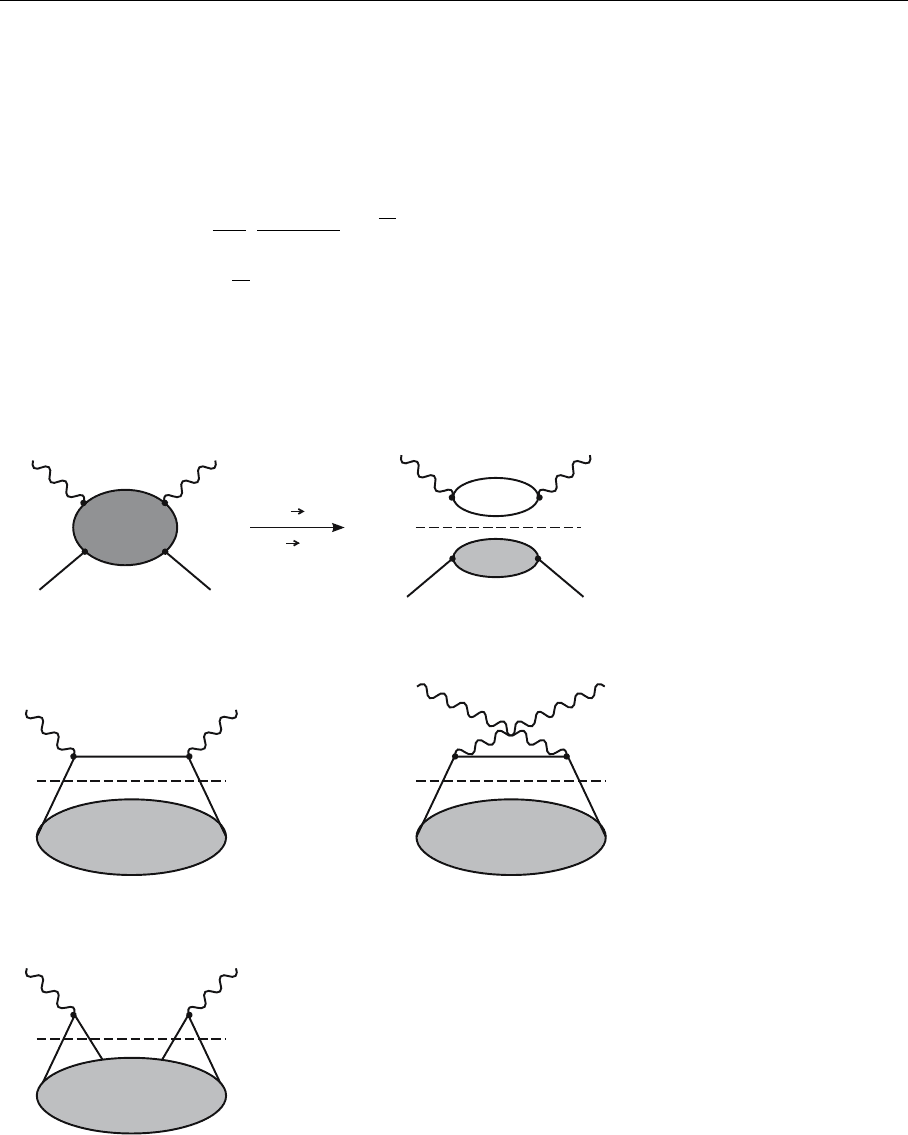
5.4 Renormalization and the Expansion Into Local Operators 321
perturbation theory, the lower part is subject to nonperturbative methods. More-
over, these nonperturbative methods can now be applied to well defined hadronic
matrix elements.
While the “hand bag” diagrams (b) and (c) contain one free quark propaga-
tor, i.e. they are singular as x
2
→0, the “cat ear” diagram (d) contains none and
therefore we can safely neglect it. It will not give a dominant contribution on the
light cone. Diagrams (b) and (c) can therefore be written as
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
x
2
→0
=
1
2π
2
i
x
α
(x
2
−iε)
2
f
ˆ
Ψ
f
(x)e
2
f
γ
µ
γ
α
γ
ν
ˆ
Ψ(0)
−
ˆ
Ψ
f
(0)e
2
f
γ
ν
γ
α
γ
µ
ˆ
Ψ(x). (5.227)
Using the identy
γ
µ
γ
α
γ
ν
=(s
µανβ
+iε
µανβ
γ
5
)γ
β
(5.228)
x
xx
x
0
00
0
d)
b) c)
a)
+
++
^
J(x)
µ
^
J(0)
ν
|PS
>
|PS
>
Q,
2
ν
8
x0
2
Fig. 5.18a–d. Diagrams oc-
curing in the analysis of
the time-ordered product
on the light cone x
2
→0.
Wavy lines denote the pho-
ton, straight lines the free
massless quark propagator
and the blob the proton state.
Diagramm (a) will only
contribute between vacuum
states and will not contribute
to lepton proton scattering
since it is disconnected. The
dashed line is a symbolic in-
dication of the separation in
perturbative and nonpertur-
bative contributions
322 5. Perturbative QCD I: Deep Inelastic Scattering
(see Excercise 5.9) we obtain
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
x
2
→0
=
ix
α
2π
2
(x
2
−iε)
2
s
µανβ
×
⎛
⎝
f
ˆ
Ψ
f
(x)e
2
f
γ
β
ˆ
Ψ(0) −
ˆ
Ψ
f
(0)e
2
f
γ
β
ˆ
Ψ(x)
⎞
⎠
−
x
α
2π
2
(x
2
−iε)
2
ε
µανβ
×
⎛
⎝
f
ˆ
Ψ
f
(x)e
2
f
γ
β
γ
5
ˆ
Ψ(0) +
ˆ
Ψ
f
(0)e
2
f
γ
β
γ
5
ˆ
Ψ(x)
⎞
⎠
.
(5.229)
We can now expand the bilocal operator
ˆ
Ψ(0)e
2
f
γ
α
ˆ
Ψ(x) =
∞
n=0
x
µ
1
···x
µ
n
n!
ˆ
Ψ(0)e
2
f
γ
α
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ(0),
ˆ
Ψ(x)e
2
f
γ
α
ˆ
Ψ(0) =
∞
n=0
x
µ
1
···x
µ
n
n!
(−1)
n
ˆ
Ψ(0)e
2
f
γ
α
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ(0),
(5.230)
where we have brought all derivatives to act on the right-hand side and have neg-
lected total derivative terms. Note that we have also included covariant derivative
terms to take interactions into account. Rearranging the equations we get
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
=
ix
α
π
2
(x
2
−iε)
2
s
µανβ
×
⎧
⎨
⎩
∞
n=1,3,5
x
µ
1
···x
µ
n
n!
f
ˆ
Ψ
f
(0)e
2
f
γ
β
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ(0)
⎫
⎬
⎭
−
ix
α
π
2
(x
2
−iε)
2
ε
µανβ
×
⎧
⎨
⎩
∞
n=0,2,
x
µ
1
···x
µ
n
n!
f
ˆ
Ψ
f
(0)e
2
f
γ
β
γ
5
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ(0)
⎫
⎬
⎭
. (5.231)
This can be compared with the general structure of the scattering tensor
(see (3.18)) (see also Sect. 5.6 where the spin-dependent structure functions are
discussed extensively)
5.4 Renormalization and the Expansion Into Local Operators 323
T
µν
=
−g
µν
+
q
µ
q
ν
q
2
˜
F
1
(x, Q
2
)
+
˜
F
2
(x, Q
2
)
p ·q
p
µ
−
p ·q
q
2
q
µ
p
ν
−
p ·q
q
2
q
ν
−iε
µνλσ
q
λ
p ·q
˜
g
1
(x, Q
2
)S
σ
+
˜
g
2
(x, Q
2
)
S
σ
− p
σ
S ·q
p ·q
, (5.232)
where
1
π
Im
˜
F
1
= F
1
, etc., according to the optical theorem. This can also be used
to identify the terms in the general representation of the time-ordered product.
Indeed, we can conclude that the spin-independent structure functions F
1
and
F
2
are somehow related to the vector operators
∼
f
e
2
f
ˆ
Ψ
f
(0)γ
α
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ
f
(0),
while the spin-dependent structure functions
˜
g
1
and
˜
g
2
are related to the anti-
symmetric part of (5.227) and therefore to the axial vector operator
∼
f
e
2
f
ˆ
Ψ
f
(0)γ
α
γ
5
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ
f
(0).
To proceed we restrict ourselves to the antisymmetric part of (5.227), which
contributes to the spin-dependent scattering.
T
ˆ
J
µ
(x)
ˆ
J
ν
(0)
A
=
−i
π
2
x
α
(x
2
−iε)
2
ε
µανβ
×
⎧
⎨
⎩
n=0,2,
x
µ
1
···x
µ
n
n!
f
ˆ
Ψ
f
(0)e
2
f
γ
β
γ
5
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ
f
(0)
⎫
⎬
⎭
. (5.233)
The time-ordered product is to be inserted between nucleon states and the
Fourier transformation has to be carried out. In doing so we have to define matrix
elements of local operators
i
n−1
PS|
ˆ
Ψ
f
(0)γ
β
γ
5
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ
f
(0)|PS
twist-2
=
S
β
p
µ
1
···p
µ
n
2A
f
n+1
, (5.234)
where we proceeded completely analogously to (5.140) and (5.166). Here is
defined as (µ
1
...µ
n
) = (1/n!)
a
permutations(µ
1
...µ
n
)
.
Again we have to take the completely symmetric part symbolized by .It
corresponds to the leading twist contribution. We will explain the notion of twist
in detail in Example 5.16. For the moment it is enough to know that leading twist
operators are those that are completely symmetric in all indices.
Unlike the case of the symmetric (in µ, ν) contribution to the scattering tensor
– due to the axial vector character of the operator – the spin vector S
β
appears in
the symmetrized product. This leads to additional complications.

324 5. Perturbative QCD I: Deep Inelastic Scattering
Let us split up the symmetrized part (writing S
β
= S
µ
1
for convenience)
S
µ
1
p
µ
2
···p
µ
n
= S
µ
1
p
µ
2
···p
µ
n
+R
µ
1
···µ
n
, (5.235)
where the residual tensor is
R
µ
1
···µ
n
=
S
µ
1
p
µ
2
···p
µ
n
−S
µ
1
···p
µ
n
=
1
n
S
µ
1
p
µ
2
···p
µ
n
+ p
µ
1
S
µ
2
···p
µ
n
+···+p
µ
1
p
µ
2
···S
µ
n
−S
µ
1
···p
µ
n
=−
n −1
n
S
µ
1
p
µ
2
···p
µ
n
+
1
n
p
µ
1
S
µ
2
···p
µ
n
+···
+
1
n
p
µ
1
p
µ
2
···S
µ
n
. (5.236)
The tensor R
µ
1
···µ
n
has no completely symmetric part, and so has one addi-
tional unit of twist. Thus the contribution of R to deep inelastic scattering is twist
three, rather than twist two, even though it comes from the matrix element of
a twist-two operator. This will contribute to the second spin-dependent structure
function
˜
g
2
. In this context we will omit R and refer the interested reader to the
literature.
15
Inserting (5.234) in (5.233) we arrive at
−i
π
2
x
α
(x
2
−iε)
2
ε
µανβ
×
⎧
⎨
⎩
n=0,2,
x
µ
1
···x
µ
n
n!
f
PS|
ˆ
Ψ
f
(0)e
2
f
γ
β
γ
5
ˆ
D
µ
1
···
ˆ
D
µ
n
ˆ
Ψ
f
(0)|PS
⎫
⎬
⎭
=
(−i)
n
π
2
x
α
(x
2
−iε)
2
ε
µανβ
n=0,2,
x
µ
1
···x
µ
n
n!
S
β
p
µ
1
···p
µ
n
2A
f
n+1
= i
d
4
x e
iqx
x
α
π
2
(x
2
−iε)
2
ε
µανβ
S
β
n=0,2,
(−i px)
n
n!
f
2A
f
n+1
e
2
f
.
(5.237)
The final formula we require is
∂
∂q
µ
1
···
∂
∂q
µ
n
=2
n
q
µ
1
···q
µ
n
∂
∂q
2
n
+trace terms , (5.238)
where we do not need the trace terms g
µ
i
µ
j
explicitely since they will be su-
pressedbypowersofQ
2
(see (5.143)). By replacing (ix
µ
) by ∂/∂q
µ
we can
write
ε
µανβ
q
α
S
β
n=0,2,
(−2p ·q)
n
n!
·2
f
e
2
f
2A
f
n+1
∂
∂q
2
n+1
d
4
x
π
2
e
iqx
(x
2
−iε)
2
.
(5.239)
15
See B. Ehrnsperger, et al.: OPE Analysis for Polarized Deep Inelastic Scattering,
Phys. Lett. B 323, 439 (1994) and references therein.
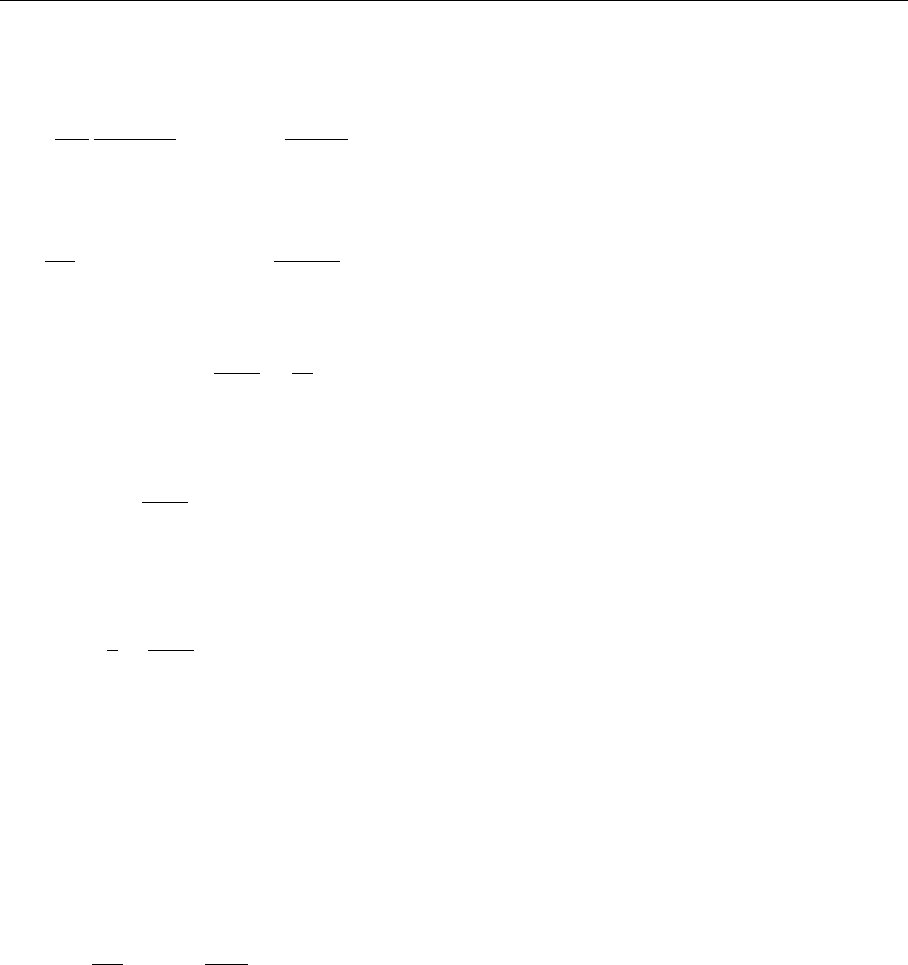
5.4 Renormalization and the Expansion Into Local Operators 325
The Fourier transformation is performed by confining the integral to d di-
mensions and making use of the formula derived in Exercise 4.6. We obtain
(d = 4 +2ε)
d
d
x
π
2
e
iqx
(x
2
−iε)
2
=−iΓ(ε)
−4πµ
2
q
2
ε
=−ilnq
2
+const. (5.240)
Performing the derivatives with respect to q
2
,
∂
∂q
2
n+1
ln(q
2
) = n!(−1)
n
1
(q
2
)
n+1
, (5.241)
we get
−iε
µανβ
q
α
S
β
n=0,2,
2p ·q
q
2
n
2
q
2
f
e
2
f
2A
f
n+1
, (5.242)
and by comparing with (5.232) we end up with
˜
g
1
=
n=0,2,
2p ·q
Q
2
n+1
f
e
2
f
2A
f
n+1
=
n=1,3,···
ω
n
⎛
⎝
f
e
2
f
2A
f
n
⎞
⎠
=
n=1,3,···
ω
n
2A
n
,
ω ≡
1
x
=
2p ·q
Q
2
, A
n
=
f
e
2
f
A
f
n
. (5.243)
This gives us again, as in (5.175) and (5.176), an expansion in ω =1/x. A
n
can be considered as a reduced matrix element. The nth term in this expansion
is due to an operator of twist two and containing n symmterized indices. The
radius of convergence of the series is |ω|=1 since this is the location of the first
singularity in the complex ω plane. This is precisely where the physical region
begins.
We can relate
˜
g
1
in the unphysical region to its value in the physical region
using contour integration. The coefficient A
n
can be extracted by the contour
integral
2A
n
=
1
2πi
C
C
˜
g
1
(ω)
dω
ω
n+1
, (5.244)
where the contour of integration is shown in Fig 5.19.
Now we have to assume that the contour at infinity does not contribute to the
integral and can be neglected. This assumption should be testable by experiment.
If the contour is important when ω →∞then this should be measurable as the
small-x behavior of the structure functions. Neglecting the contour at infinity we

326 5. Perturbative QCD I: Deep Inelastic Scattering
1-1
C
w
Fig. 5.19. Integration con-
tour in (5.244). The circle
around the origin is de-
formed to pick up the con-
tributions along the real axis
can write
2A
n
=
1
2πi
⎡
⎣
∞
1
dω
ω
n+1
[
˜
g
1
(ω +iε) −
˜
g
1
(ω −iε)
]
+
−1
−∞
dω
ω
n+1
[
˜
g
1
(ω +iε) −
˜
g
1
(ω −iε)
]
⎤
⎦
=
1
π
∞
1
dω
1
2i
˜
g
1
(ω +iε) −
˜
g
∗
1
(ω +iε)
·
1
ω
n+1
+
1
π
−1
−∞
dω
1
2i
˜
g
1
(ω +iε) −
˜
g
∗
1
(ω +iε)
·
1
ω
n+1
=
∞
1
dω
ω
n+1
˜
g
1
(ω) +
1
−∞
dω
ω
n+1
˜
g
1
(ω)
=
1
−1
dxg
1
(x)x
n−1
=2
1
0
dxg
1
(x)x
n−1
, n = odd , (5.245)
where g
1
(x) is now the physical measurable structure function. In deriving the
above relation we made use of the optical theorem W
µν
=
1
π
T
µν
and of g
1
(x) =
g
1
(−x), which follows from crossing symmetry W
µν
(q) =−W
νµ
(−q) and the
explicit decomposition of the scattering tensor (5.232). To be explicit we write

5.4 Renormalization and the Expansion Into Local Operators 327
W
µν
(q) =
1
2π
d
4
x e
iqx
PS |[
ˆ
J
µ
(x),
ˆ
J
ν
(0)]|PS
W
µν
(−q) =
1
2π
d
4
y e
−iqy
PS |[
ˆ
J
µ
( y),
ˆ
J
ν
(0)]|PS
=
1
2π
d
4
y e
iqy
PS |[
ˆ
J
µ
(−y),
ˆ
J
ν
(0)]|PS
=
1
2π
d
4
y e
iqy
PS |[
ˆ
J
µ
(0),
ˆ
J
ν
( y)]|PS
=−
1
2π
d
4
y e
iqy
PS |[
ˆ
J
ν
( y),
ˆ
J
µ
(0)]|PS
=−W
νµ
(q).
From the decomposition of the scattering tensor (5.232) it follows that g
1
(x) =
g
1
(−x) as well as F
1
(x) =−F
1
(−x).
Thus we arrive at the final equation
A
n
=
1
0
dxx
n−1
g
1
(x), (5.246)
which relates the measurable moments of the structure function g
1
(x) to the ma-
trix elements of operators defined in (5.234), which are calculable, at least in
principle.
This is a prototype of a so called moment sum rule, which relates a quantity
defined at high energy such as g
1
to a low-energy quantity, the zero momentum
transfer matrix element of a local operator. One can derive sum rules in QCD
only for even moments of F
1
and the odd moments of g
1
; there are no sum rules
for the other moments. This is due to the symmetry properties of the structure
functions under crossing, g
1
(x) = g
1
(−x) and F
1
(x) =−F
1
(−x).
The only questionable assumption in the derivation of the sum rule is that
the contour at infinity does not contribute to the integral. Indeed, the sum rules
(5.246) become more convergent for the higher moments. Therefore any prob-
lem with convergence will hopefully occur only for the lowest few moments.
Finally, we remember that we performed the calculation above with the
free quark propagator; O(α
s
) corrections are neglected as well as higher twist
operators. The full sum rule should read
1
0
dxx
n−1
g
1
(x, Q
2
) = C
n
α
s
(Q
2
),
Q
2
µ
2
A
n
(µ
2
) +O
1
Q
2
, (5.247)
where C
n
α
s
(Q
2
), Q
2
/µ
2
is the coefficient function which can be calculated
order by order in perturbation theory. In the following, we will demonstrate how
the coefficient functions are calculated.
