Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


298 5. Perturbative QCD I: Deep Inelastic Scattering
the polarizations of the nucleon the only Lorentz vectors available for this pur-
pose is P
µ
, the momentum vector of the nucleon, and the metric tensor g
µ
i
µ
j
.
Trace terms which contain one or more factors of g
µ
i
µ
j
will produce powers
of x
2
when contracted with x
µ
i
x
µ
j
in (5.138) and will therefore be less singu-
lar near the light cone x
2
∼0. Consequently, such terms are less important in
the Bjorken limit Q
2
→∞.
The x integration in (5.138) leads to a replacement of x
µ
1
x
µ
2
...x
µ
n
by the
corresponding q components. A Fourier transformation gives
x
µ
1
x
µ
2
...x
µ
n
→(...)·q
µ
1
q
µ
2
...q
µ
n
. (5.141)
Hence (5.140) is contracted with q
µ
1
q
µ
2
...q
µ
n
. It then follows that
q
µ
i
q
µ
j
P
µ
i
P
µ
j
q
µ
i
q
µ
j
M
2
g
µ
i
µ
j
=
ν
2
−Q
2
M
2
=−
ν
2M
2
1
x
→∞ (5.142)
for ν, Q
2
→∞,andx fixed. Thus all the remaining terms on the right-hand side
of (5.140) are suppressed by powers of 1/Q
2
(higher twist):
1
2
pol.
N(P)|
ˆ
O
n
µ
1
... µ
n
β
|N(P) →A
(n)
P
µ
1
P
µ
2
...P
µ
n
P
β
+... , (5.143)
W
µµ
=
1
2π
x
2
≥0
d
4
x exp
(
iq ·x
)
n odd
1
n!
x ·P
2
n
s
µαµ
β
P
β
A
(n)
×
1
π
∂
α
ε(x
0
)δ(x
2
)
+... (5.144)
=
1
2π
x
2
≥0
d
4
x exp
(
iq ·x
)
n odd
(finite term) ×(divergent term) +... .
We have succeeded in splitting up the contributions to W
µµ
into a finite and
a divergent factor
1
π
∂
α
ε(x
0
)δ(x
2
)
. The whole dependence on the specific
process under consideration is related to the finite factor whereas the divergent
factor always remains the same. This seperation of divergent current commuta-
tors into an operator with finite matrix elements specific for the hadron under
consideration and a constant divergent function is the basic idea of the expansion
into local operators.
One can ask what is the practical use of the formal expansion (5.141). As
a first simple answer we wish to show that the main statements of the parton
model can be immediately derived from this equation. The simple parton model
assumes noninteracting constituents, which correspond exactly to the use of the
free current commutator. Let us consider the relation
n odd
x ·P
2
n
A
(n)
n!
=−
dξ exp
(
ix ·ξP
)
f(ξ) , (5.145)

5.4 Renormalization and the Expansion Into Local Operators 299
with
f(η) =−
1
2π
d(x · P)
n odd
x · P
2
n
A
(n)
n!
exp
(
−ix ·Pη
)
. (5.146)
Indeed, substituting (5.146) into the right-hand side of (5.145) yields exactly the
verification of the identity (5.145). Inserting this into the hadron scattering tensor
(5.144), one obtains
W
µµ
=
−1
2π
d
4
x
dξ exp
(
ix ·(q +ξP)
)
s
µαµ
β
× P
β
f(ξ)
1
π
∂
α
ε(x
0
)δ(x
2
)
. (5.147)
Using (see Exercise 5.10)
d
4
x exp
(
ix ·(q +ξP)
)
δ(x
2
)ε(x
0
) = i4π
2
δ
(q +ξP)
2
ε(q
0
+ξ P
0
)
(5.148)
and partial integration yields
W
µµ
=−2
dξ s
µαµ
β
P
β
f(ξ)(q +ξP)
α
δ
(q +ξP)
2
ε(q
0
+ξ P
0
).
(5.149)
The argument of the δ function simplifies to
(q +ξP)
2
=q
2
+ξ
2
M
2
+2ξq · P ≈−Q
2
+ξ2ν =
Q
2
x
(ξ −x), (5.150)
W
µµ
=−2s
µαµ
β
P
β
f(x)
x
Q
2
(q +xP)
α
=−2(g
µα
g
µ
β
+g
µ
β
g
µ
α
−g
µµ
g
α
β
)P
β
(q +xP)
α
x
Q
2
f(x)
=−2
x
Q
2
f(x)
(q +xP)
µ
P
µ
+P
µ
(q +xP)
µ
−g
µµ
(xM
2
+ P ·q)
. (5.151)
Note that x = Q
2
/2ν denotes the Bjorken-variable. Since W
µµ
is multiplied by
the lepton scattering tensor L
µµ
, we can omit all terms proportional to q
µ
and
q
µ
, because of
q
µ
L
µµ
=q
µ
L
µµ
= 0 . (5.152)
With ν = P ·q this yields
W
µµ
→−2
x
Q
2
f(x)
−g
µµ
(xM
2
+ν) +2xP
µ
P
µ
≈−2
x
Q
2
f(x)
−g
µµ
ν +2xP
µ
P
µ
. (5.153)
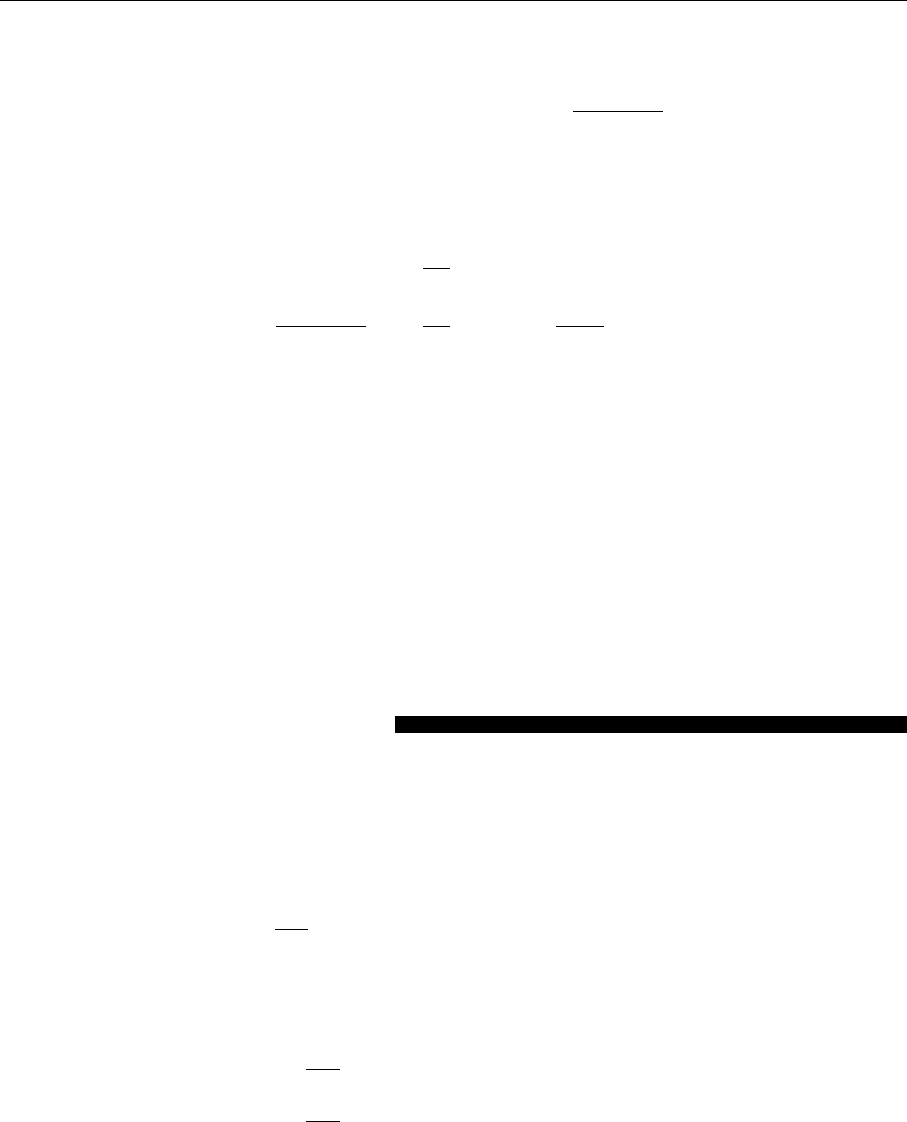
300 5. Perturbative QCD I: Deep Inelastic Scattering
In an analogous way, i.e., by neglecting all terms proportional to q
µ
or q
µ
,we
obtain from (3.18)
W
µµ
→−g
µµ
W
1
(Q
2
,ν)+ P
µ
P
µ
W
2
(Q
2
,ν)
M
2
N
. (5.154)
Comparison of (5.153) with (5.154) shows that W
1
(Q
2
, x) and W
2
(Q
2
, x) in
fact depend only on x. Furthermore we get the Callan–Gross relation . For that
purpose we also remember the definition (3.43) and identity
W
1
(Q
2
,ν)=−2
x
Q
2
f(x)ν =: F
1
(x), (5.155)
W
2
(Q
2
,ν)
M
2
N
=−2
x
Q
2
f(x) ·2x =:
F
2
(x)
ν
⇒ F
2
(x) = 2xF
1
(x). (5.156)
This was just a simple example. In general the operator product expansion (OPE)
provides two major results.
1. It gives a formal expression for all the terms that can occur. This allows
us to analyze in a systematic way the terms contributing to a given power of
1/Q
2
. Furthermore it generates relations between various phenomenological
expressions such as the structure functions.
2. For the individual terms appearing in the 1/Q
2
expansion the OPE gives
the corresponding correlators. This shows to what property of the (unknown)
exact wave function a given observable is sensitive and allows us to calculate
it in an appropriate model (i.e., a model which should describe the specific
correlation in question realistically).
EXERCISE
5.10 The Proof of (5.148)
Problem. Prove (5.148) by replacing (q +ξP)
µ
by k
µ
and evaluating the
Fourier transformation of (5.148), i.e., by proving that
i
4π
2
exp
(
−ik ·x
)
δ(k
2
)ε(k
0
)d
4
k = δ(x
2
)ε(x
0
). (1)
Solution. Performing the k
0
integration turns the left-hand side into
I =
i
4π
2
exp
(
−i(k
0
x
0
−k ·x)
)
δ(k
2
0
−k
2
)ε(k
0
)dk
0
d
3
k
=
i
4π
2
exp
(
−i(k
0
x
0
−k ·x)
)
δ
(
(k
0
−k)(k
0
+k)
)
ε(k
0
)dk
0
d
3
k

5.4 Renormalization and the Expansion Into Local Operators 301
=
i
4π
2
1
2k
exp
−ik(x
0
−r cos θ)
−exp
+ik(x
0
+r cos θ)
d
3
k (2)
with
k :=
"
k
2
,
r =
"
x
2
,
k·x = kr cos θ. (3)
We evaluate the angular integration
I =
i
2π
∞
0
dk
k
2
2k
1
ikr
exp
−ik(x
0
−r)
−exp
−ik(x
0
+r)
−
1
ikr
exp
ik(x
0
+r)
−exp
ik(x
0
−r)
=
1
4πr
∞
−∞
dk
exp
−ik(x
0
−r)
−exp
ik(x
0
+r)
(4)
and obtain a difference of δ functions, which yields the postulated result:
I =
2π
4πr
δ(x
0
−r) −δ(x
0
+r)
= δ(x
2
)
x
0
=r
− δ(x
2
)
x
0
=−r
=δ(x
2
)ε(x
0
). (5)
Let us discuss next how the expansion of W
µµ
changes if in (5.144) we replace
the free by the exact current commutator, i.e., if we take the quark interactions
into account. This corresponds in lowest order to the transition from the simple
parton model to the GLAP equations.
The bilocal operators
ˆ
Ψ
x
2
ˆ
Ψ
−
x
2
are not gauge invariant. In order to
achieve that, the derivatives in
ˆ
O
n
µ
1
µ
2
...µ
n
β
have to be replaced by covariant
derivatives
ˆ
D
µ
. For the sake of simplicity all derivatives that operate to the left
are partially integrated such that they act to the right:
∂
µ
−
←−
∂
µ
→2∂
µ
, (5.157)
ˆ
O
n
µ
1
µ
2
...µ
n
β
→2
n
ˆ
D
µ
1
ˆ
D
µ
2
...
ˆ
D
µ
n
γ
β
. (5.158)
Exercise 5.10
302 5. Perturbative QCD I: Deep Inelastic Scattering
In this way, i.e. by measuring gauge-invariant bilocal structures, the interactions
with the gauge field A
a
µ
are appearing. In the general interacting case, i.e. if
instead of the simple handbag diagrams
+
more complicated processes like
etc. are considered, some modified divergent function takes the place of
∂
α
[ε(x
0
)δ(x
2
)]. The leading divergence remains the same, but additional terms
occur. Also the appearance of s
µαµ
β
was due to the specific situation of the free
case (see (5.130)). Now the general form of (5.138) is
W
µµ
=
1
2π
d
4
x exp
(
iq ·x
)
j
n
−g
µµ
x
µ
1
x
µ
2
...x
µ
n
i
n
C
(n)
1, j
(x)
+
g
µµ
1
g
µ
µ
2
x
µ
3
x
µ
4
...x
µ
n
i
n−2
C
(n)
2, j
(x)
×
1
2
pol.
N|
ˆ
O
(n), j
µ
1
µ
2
...µ
n
|N . (5.159)
The general form again is determined by the requirements of Lorentz covari-
ance and current conservation which lead in the unpolarized case to one structure
function proportional to g
µµ
and another structure function proportional to
P
µ
P
µ
(see (5.154)). Instead of the tensor s
µαµ
β
in (5.133) there are now two
independent contributions which in coordinate space are proportional to g
µµ
and x
µ
x
µ
, respectively. The C
(n)
1 j
and C
(n)
2 j
are divergent functions. They are
independent Wilson coefficients corresponding to F
1
(x, Q
2
) and F
2
(x, Q
2
),
respectively.
5.4 Renormalization and the Expansion Into Local Operators 303
Again in leading order all terms containing g
ij
can be neglected, since the ma-
trix element of the operator
ˆ
O
(n) j
is proportional to P
µ
1
P
µ
2
...P
µ
n
. Therefore
all terms with g
µ
i
µ
j
yield much smaller contributions than those with x
µ
i
x
µ
j
:
x
2
g
µ
i
µ
j
P
µ
i
P
µ
j
x
µ
i
x
µ
j
P
µ
i
P
µ
j
Fourier transformation
−−−−−−−−−−−−−−−−−−→
q
2
P
2
(q · P)
2
=−
M
2
Q
2
ν
2
=−
2M
2
x
ν
→0 . (5.160)
Since we do not know the expansion analogous to (5.138), we have to regard
the divergent functions of the two terms C
(n)
1
and C
(n)
2
that occur as different.
Furthermore we must take into account that the operator
ˆ
O
(n)
can now change
the flavor of a quark and can in addition act on the gluons. Consequently we have
to distinguish between three operators:
j = q :
ˆ
O
(n),q
µ
1
µ
2
...µ
n
=
i
n−1
2n!
$
γ
µ
1
ˆ
D
µ
2
ˆ
D
µ
3
...
ˆ
D
µ
n
+permutations of vector indices
%
(5.161)
acts on quark states (SU(3) singlet);
j = NS :
ˆ
O
(n),NS
µ
1
µ
2
...µ
n
,a
=
i
n−1
2n!
)
ˆ
λ
a
2
γ
µ
1
ˆ
D
µ
2
ˆ
D
µ
3
...
ˆ
D
µ
n
+ permutations
*
(5.162)
acts on quark states and can change the flavor (SU(3) octet); and
j = G :
ˆ
O
(n),G
µ
1
µ
2
...µ
n
(5.163)
acts on the gluon states
¯
F
µν
|
ˆ
O
(n),G
µ
1
µ
2
...µ
n
|
¯
F
µν
=
i
n−2
n!
tr
$
¯
F
µµ
1
ˆ
D
µ
2
ˆ
D
µ
3
...
ˆ
D
µ
n−1
¯
F
µ
µ
n
+ permutations
%
. (5.164)
Here we have chosen the standard normalizations for C
1
and C
2
, which are called
coefficient functions. Since P
µ
is the only four-vector that occurs in
1
2
pol.
N(P)|
ˆ
O
(n), j
µ
1
µ
2
...µ
n
|N (P) , (5.165)
we can expand (5.165) into powers of P
µ
.Againg
µ
i
µ
j
P
2
is negligible compared
to P
µ
i
P
µ
j
and therefore the leading term is
1
2
pol.
N(P)|
ˆ
O
(n), j
µ
1
µ
2
...µ
n
|N (P) =A
(n), j
P
µ
1
P
µ
2
...P
µ
n
, (5.166)

304 5. Perturbative QCD I: Deep Inelastic Scattering
and
W
µµ
=
1
2π
d
4
x exp
(
iq ·x
)
j
n
−g
µµ
(x · P)
n
i
n
C
(n)
1, j
(x)
+ P
µ
P
µ
(x ·P)
n−2
i
n−2
C
(n)
2, j
(x)
A
(n), j
. (5.167)
Now we substitute for
x
µ
exp
(
iq ·x
)
=−i
∂
∂q
µ
exp
(
iq ·x
)
=−2iq
µ
∂
∂q
2
exp
(
q ·x
)
, (5.168)
and therefore
x
µ
1
...x
µ
n
→(−i)
n
∂
∂q
µ
1
...
∂
∂q
µ
n
=(−2i)
n
q
µ
1
...q
µ
n
∂
∂q
2
n
+ trace terms , (5.169)
giving
W
µµ
=
1
2π
j,n
⎡
⎣
−g
µµ
(2q · P)
n
∂
∂q
2
n
d
4
x exp
(
iq ·x
)
C
(n)
1, j
(x)
+ P
µ
P
µ
(2q · P)
n−2
∂
∂q
2
n−2
d
4
x exp
(
iq ·x
)
C
(n)
2, j
(x)
⎤
⎦
A
(n), j
=
1
2π
j,n
⎡
⎣
−g
µµ
2q · P
Q
2
n
(Q
2
)
n
∂
∂q
2
n
×
d
4
exp
(
iq ·x
)
C
(n)
i, j
(x) +
P
µ
P
µ
2q · P
2q · P
Q
2
n−1
×(Q
2
)
n−1
∂
∂q
2
n−2
d
4
x exp
(
iq ·x
)
C
(n)
2, j
(x)
⎤
⎦
. (5.170)
Just as in the free case we can read off the structure functions F
1
(x) and F
2
(x),
which in their most general form are now
F
1
(x) =
1
2π
j,n
2q · p
Q
2
n
(Q
2
)
n
∂
∂q
2
n
×
d
4
x exp
(
iq ·x
)
C
(n)
1, j
(x)A
(n), j
, (5.171)
F
2
(x) =
1
4π
j,n
'
2q · p
Q
2
n−1
(Q
2
)
n−1
∂
∂q
2
n−2
(
×
d
4
x exp
(
iq ·x
)
C
(n)
2, j
(x)A
(n), j
. (5.172)

5.4 Renormalization and the Expansion Into Local Operators 305
To simplify these expressions we define the nth moment of the coefficient
functions
˜
C
(n)
1, j
(Q
2
) =
1
4π
(Q
2
)
n
∂
∂q
2
n
d
4
x exp
(
iq ·x
)
C
(n)
1, j
(x) (5.173)
and
˜
C
(n)
2, j
(Q
2
) =
1
16π
(Q
2
)
n−1
∂
∂q
2
n−2
d
4
x exp
(
iq ·x
)
C
(n)
2, j
(x). (5.174)
Now the structure functions are
F
1
(x, Q
2
) = 2
j,n
x
−n
˜
C
(n)
1, j
A
(n), j
, (5.175)
F
2
(x, Q
2
) = 4
j,n
x
−n+1
˜
C
(n)
2, j
A
(n), j
. (5.176)
Note that (5.175) and (5.176) now have the form of a Taylor expansion in 1/x.
However, physically 0 < x < 1, so that a series in 1/x hardly makes sense. The
key observation is, however, that this expansion which is mathematically correct
in the unphysical region of the current commutator 1 < x < ∞ can be analyti-
cally continued with the help of a dispersion relation. This will be done below in
(5.199) to (5.205). What have we gained by this general formulation? We have
expressed the structure functions by sums over products of divergent functions
˜
C
1, j
,
˜
C
2, j
and unknown constants A
(n), j
. The only thing we know is that the
C
1, j
, C
2, j
are independent of the hadron considered. Therefore the
˜
C
1, j
,
˜
C
2, j
can only depend on Q
2
and the constants of the theory, which are the coupling
constant g and the renormalization point µ:
˜
C
(n)
1, j
=
˜
C
(n)
1, j
(Q
2
, g,µ) ,
˜
C
(n)
2, j
=
˜
C
(n)
2, j
(Q
2
, g,µ) . (5.177)
In addition, the constants A
(n), j
are matrix elements of certain operators sand-
wiched between nucleon states. Therefore all bound state complexities inherent
in the |N( p) state are buried in these matrix elements. Hence, we know that
the constants A
(n), j
are characteristic for the hadronic state under considera-
tion. Of course, all quantities can be approximately evaluated, the
˜
C
1, j
,
˜
C
2, j
reliably by means of perturbation theory from the free current commutator
ˆ
J
µ
(x),
ˆ
J
ν
(0)
(see (5.126)) and the QCD Feynman rules. The A
(n), j
,however,
are truely nonperturbative and can only be obtained from a phenomenological
model of the nucleon or from lattice QCD or from a sum-rule calculation, using
(5.166). The finite matrix elements A
(n), j
thus contain information about the in-
ner structure of the nucleons, for example. To obtain the perturbative expansion
of the
˜
C
(n)
1, j
,
˜
C
(n)
2, j
for the structure functions, we have to repeat the calculation in
306 5. Perturbative QCD I: Deep Inelastic Scattering
Sect. 5.1, which again leads to the GLAP equations. An advantage of this gen-
eral OPE formulation is that formal features of the
˜
C
1, j
,
˜
C
2, j
can be deduced and
relationships between different quantities can be established for the full nonper-
turbative expressions. The most important way to deduce information about the
coefficient functions is to consider their renormalization behavior.
Here we only need to know that QCD is renormalizable and that for a given
renormalization scheme carried out for a specific kinematic the bare coupling
constants, Green functions, and so on are replaced by the renormalized ones.
The renormalization schemes differ by the chosen kinematics, which can in
general be characterized by a momentum parameter µ
2
. Correspondingly the
renormalized functions
˜
C
1
,
˜
C
2
in (5.177) can also be written as
˜
C
(n)
i, j
(Q
2
, g,µ)=
k
Z
(n)
jk
(g
0
,µ)
˜
C
(n)
i,k
(Q
2
, g
0
)
unren.
, (5.178)
g = g(g
0
,µ,Q
2
).
Equation (5.178) takes care of the fact that renormalization in general mixes dif-
ferent
˜
C
(n)
j
, j =q,NS,G. This can be understood qualitatively by taking into
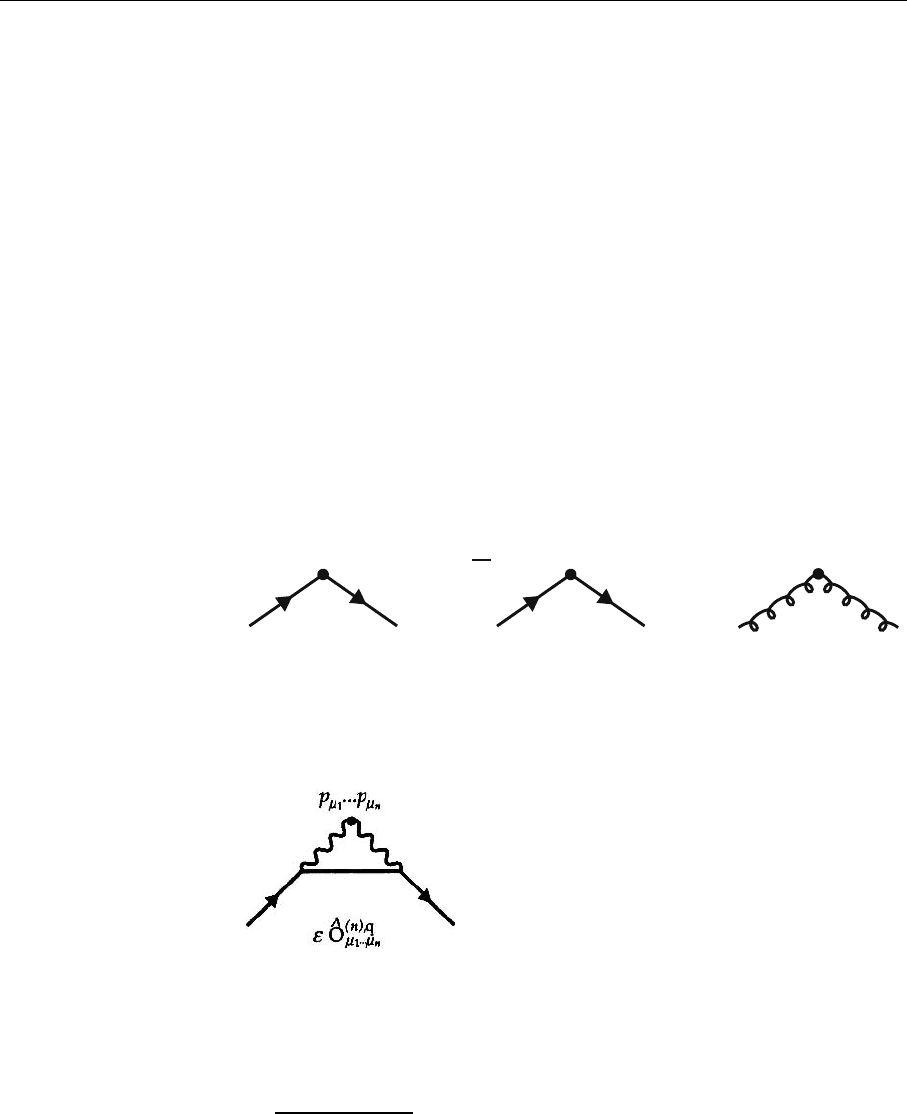
account that not only do the graphs
g
mm m
12
p ...p
n
g
mm m
12
p ...p
n
p ...p
mm
1 n
qq
e O
^
(n),q
e O
^
(n)NS
e O
^
(n)G
mm
1
...
n
mm
1
...
n
mm
1
...
n
l
a
2
G
occur, but also, for example, the graph
Hence the sum over k =q,NS,G occurs on the right-hand side of (5.178).
Since the physical theory must not depend on the renormalization point µ,we
can demand that
d
˜
C
(n)
ij
(Q
2
, g,µ)
dµ
= 0 .

5.4 Renormalization and the Expansion Into Local Operators 307
Now the total derivative is split up into partial derivatives.
d
dµ
˜
C
(n)
i, j
(Q
2
, g,µ)=
∂g
∂µ
∂
∂g
+
∂
∂µ
˜
C
(n)
i, j
(Q
2
, g,µ)
=
k
∂Z
(n)
jk
∂µ
˜
C
(n)
i,k
(Q
2
, g
0
)
unren.
=
klm
∂Z
(n)
jk
∂µ
Z
(n)
−1
kl
Z
(n)
lm
˜
C
(n)
i,m
(Q
2
, g
0
)
unren.
=
l
'
k
∂Z
(n)
jk
∂µ
Z
(n)
−1
kl
(
˜
C
(n)
i,l
(Q
2
, g,µ) .
Defining
γ
(n)
jl
:=−µ
k
∂Z
(n)
jk
∂µ
Z
(n)
−1
kl
= γ
(n)
jl
(g,µ) (5.179)
yields
l
µ
∂g
∂µ
∂
∂g
+µ
∂
∂µ
δ
jl
+γ
(n)
jl
˜
C
(n)
i,l
(Q
2
, g,µ)= 0 . (5.180)
The term ∂g/∂µ, i.e., the dependence of the coupling constant on the renormal-
ization point, is a fixed characteristic function for every field theory. It is referred
to as the β function:
β(g) = µ
∂g
∂µ
. (5.181)
In the case of QCD, perturbation theory yields (see Exercise 5.11)
β(g) =−
11 −
2
3
N
f
g
3
(4π)
2
−
102 −
38
3
N
f
g
5
(4π)
4
+O(g
7
),
(5.182)
where N
f
denotes the number of quark flavors.
