Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

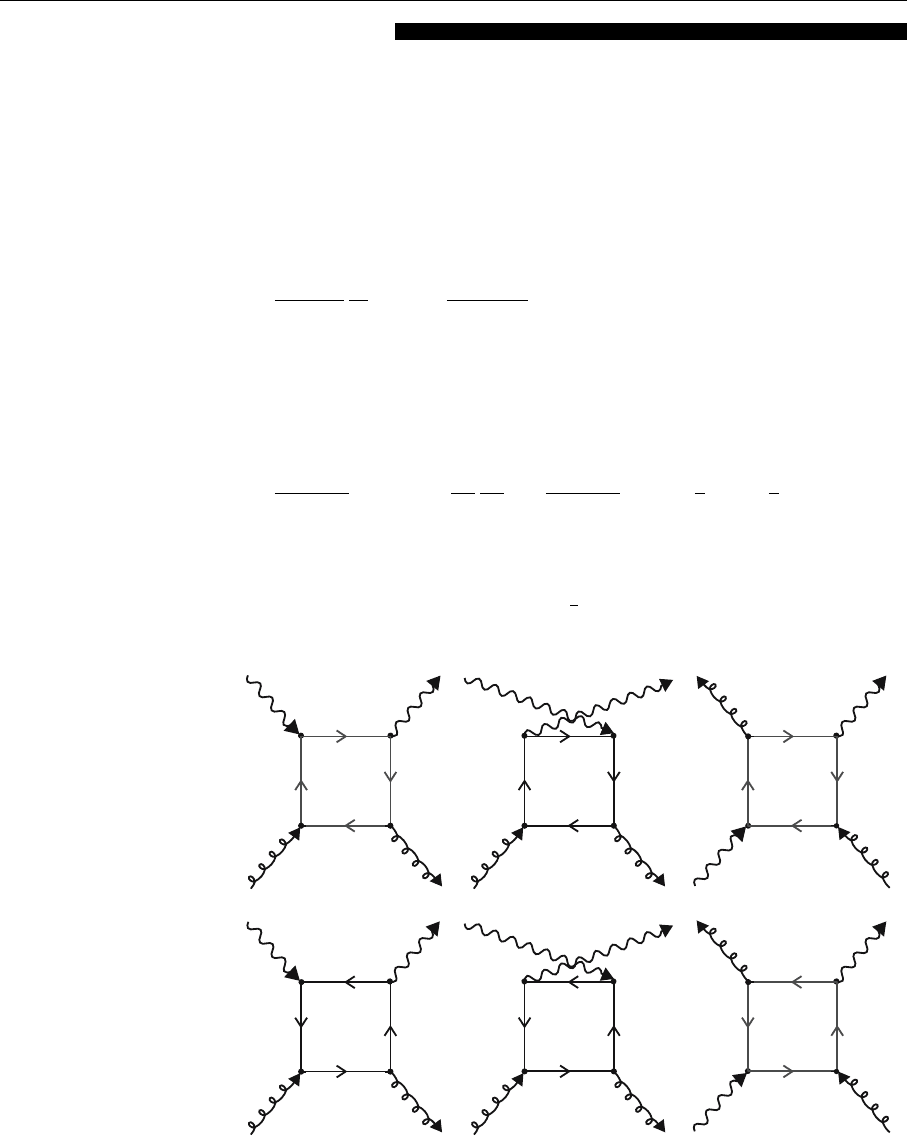
338 5. Perturbative QCD I: Deep Inelastic Scattering
qq
pp
Fig. 5.24. Diagrams con-
tributing in O(α
s
) to the
virtual photon–gluon scat-
tering.
EXERCISE
5.13 Calculation of the Gluonic Contribution to F
L
(x, Q
2
)
Problem. Calculate in the same way as done in the foregoing text the contribu-
tion to F
L
due to photon–gluon scattering via a quark loop. The corresponding
diagrams are shown in the figure. A usefull trick is to express the product of two
propagators involving an onshell momentum p
2
=0as
1
(k + p)
2
1
k
2
=
1
0
du
1
(k +up)
4
.
Prove this formula and find its generalization.
Solution. The color factor for the diagrams coming from the Gell-Mann matri-
ces at the quark–gluon vertices can be written as
1
(N
2
−1)
A
B
tr
λ
A
2
λ
B
2
=
1
(N
2
−1)
A
B
1
2
δ
AB
=
1
2
, (1)
where we summed over outgoing gluon colors and averaged over the incoming
ones. Together with a factor N
f
, which is due to the sum over flavors in the quark
loop, this yields an overall factor T
f
=
1
2
N
f
.
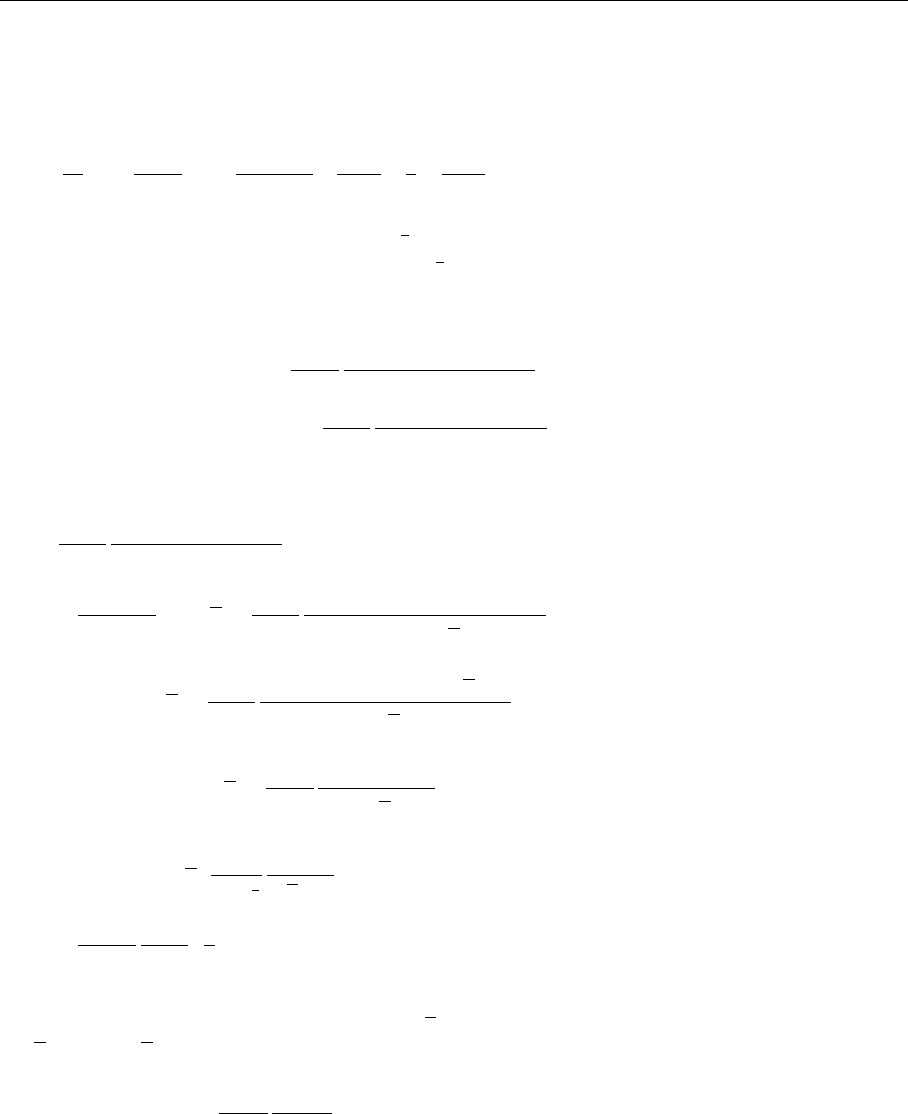
5.5 Calculation of the Wilson Coefficients 339
We start with the first diagram which we name T
(1)gg
µν
(direct). In the usual
way the exchange term can be found by substituting µ ↔ ν and q ↔−q.
According to the Feynman rules we write
T
(1)gg
µν
(direct)
=i
g
2
2
T
f
d
4
k
(2π)
4
tr
γ
µ
i
p/ +q/ +k/
γ
ν
i
p/ +k/
γ
α
i
k/
γ
β
i
p/ +k/
−g
αβ
, (2)
where we have inserted an additional factor of
1
2
due to the averaging over the
gluon spin and used
−g
αβ
for the polarization sum
1
2
ε
α
(k)ε
β
(k) =−g
αβ
/2.
Again we compute i times the time-ordered product. Projecting with p
µ
p
ν
we
find, with γ
α
k/γ
α
=−2k/,
p
µ
p
ν
T
(1)gg
µν
(direct) = ig
2
T
f
d
4
k
(2π)
4
tr
[
p/(q/ +k/) p/k/k/k/
]
( p +q +k)
2
( p +k)
4
k
2
= 8ig
2
T
f
d
4
k
(2π)
4
p ·(q +k)(kp)
( p +q +k)
2
( p +k)
4
. (3)
The integral can be evaluated in the usual way
d
4
k
(2π)
4
(k +q)
α
k
β
( p +k +q)
2
( p +k)
4
=
Γ(3)
Γ(1)Γ(2)
1
0
duu
d
4
k
(2π)
4
(k +q)
α
k
β
u(p +k +q)
2
+u( p +k)
2
3
=Γ(3)
1
0
duu
d
4
k
(2π)
4
[k −( p +uq)]
α
[k − p +uq)]
β
k
2
−uuQ
2
3
=−q
α
q
β
Γ(3)
1
0
duu
d
4
k
(2π)
4
1
k
2
−uuQ
2
3
+O
g
αβ
, p
α
p
β
=−q
α
q
β
1
0
duuu
i
(4π)
d
2
1
uuQ
2
+O
g
αβ
, p
α
p
β
=
−q
α
q
β
Q
2
i
(4π)
2
·
1
2
+O
g
αβ
, p
α
p
β
. (4)
We performed the usual Feynman parametrization (see Exercise 4.7)
and wrote the denominator as
u(p +k +q)
2
+u( p +k)
2
=
(k + p +uq)
2
+ uuq
2
,whereu = 1 −u. Inserting this into (3) yields
p
µ
p
ν
T
(1)gg
µν
(direct) =
4g
2
T
f
(4π)
2
( p ·q)
2
Q
2
. (5)
Exercise 5.13

340 5. Perturbative QCD I: Deep Inelastic Scattering
Exercise 5.13
q
q
p
p
q+k+p
q+kk+p
k
Fig. 5.25. Second type of di-
agrams that contribute to vir-
tual photon–gluonscattering.
Taking the other four diagrams of the same type into account, i.e. the ex-
change term and the opposite direction of the fermion loop, we get a contribution
to F
L
(5.251) of
˜
F
(1)g
L
2x
=
16g
2
T
f
(4π)
2
, (6)
which is, however, independent of ω, i.e. proportional to ω
0
.However,thesum
in (5.258) starts as ω
2
, i.e. after transformation to Bjorken x these four diagrams
do not contribute to the measurable structure function.
The remaining diagrams are sligthly more complicated to evaluate. They are
shown in the last row of the figure at the beginnning of this exercise. We write
according to the Feynman rules (see Fig. 5.25)
T
(1)gg
µν
(direct)
=
1
2
T
f
g
2
i
d
4
k
(2π)
4
tr
γ
µ
i
q/ +k/
γ
α
i
q/ +k/ + p/
γ
ν
i
k/ + p/
γ
β
i
k/
−g
αβ
. (7)
Projecting onto F
L
we write
p
µ
p
ν
T
(1)gg
µν
(direct) =−
1
2
T
f
g
2
i
×
d
4
k
(2π)
4
tr
[
p/(q/ +k/)γ
α
(q/ +k/ + p/) p/(k/ + p/)γ
α
k/
]
(q +k)
2
(q +k + p)
2
(k + p)
2
k
2
=+T
f
g
2
i
d
4
k
(2π)
4
tr
[
p/(q/ +k/)k/ p/(q/ +k/)k/
]
(q +k)
2
(q +k + p)
2
(k + p)
2
k
2
,
(8)
whereweusedp/
2
= p
2
= 0andγ
α
γ
µ
γ
ν
γ
γ
α
=−2γ
γ
ν
γ
µ
. The trace can be
further simplified as
tr
[
p/(q/ +k/)k/ p/(q/ +k/)k/
]
=2k · ptr
[
p/(q/ +k/)(q/ +k/)k/
]
−tr
[
p/(q/ +k/) p/k/(q/ +k/)k/
]
=8(k · p)
2
(q +k)
2
−2 p ·(q +k)tr
[
p/k/(q/ +k/)k/
]
=8(k · p)
2
(q +k)
2
−16 p ·(q +k)(k ·q)( p ·k)
−16 p(q +k) p ·kk
2
+8[p ·(q +k)]
2
k
2
, (9)
so that we get
p
µ
p
ν
T
(1)gg
µν
(direct) =8g
2
iT
f
[
I
1
(q, p) + I
1
(−q, p)
−2I
2
(q, p) −2I
3
(q, p)
]
, (10)
5.5 Calculation of the Wilson Coefficients 341
where
I
1
(q, p) =
d
4
k
(2π)
4
(k · p)
2
(q +k + p)
2
(k + p)
2
k
2
,
I
1
(−q, p) =
d
4
k
(2π)
4
( p ·(q +k))
2
(q +k)
2
(q +k + p)
2
(k + p)
2
=
d
4
k
(2π)
4
( p ·k)
2
(k + p)
2
(k + p −q)
2
k
2
,
I
2
(q, p) =
d
4
k
(2π)
4
p ·(q +k) p ·k
(q +k)
2
(q +k + p)
2
(k + p)
2
,
I
3
(q, p) =
d
4
k
(2π)
4
p ·(q +k)k ·qp·k
(q +k)
2
(q +k + p)
2
(k + p)
2
k
2
. (11)
The integrals I
1
(q, p) and I
2
(q, p) are of the same type as we had before (see
(5.265)). Using suitable substitutions we can therefore deduce the corresponding
results directly from the previous calculation of F
q
L
. Comparing I
1
(q, p) with
(5.265) we see that ( p +k)
2
in the denominator comes now with a power of 1
instead of 2. Therefore we copy from (5.269) with evident changes and get
I
1
(q, p) = ( p ·q)
2
Γ(3)
1
0
du
1
0
dvvv
2
d
4
k
(2π)
4
1
(k
2
−vvQ
2
(1 −ωu))
3
.
(12)
We changed Γ(4) →Γ(3) corresponding to the different power and we
omitted the Feynman parameter (u
v), which came from the parametrization of
( p +k)
4
in (5.265), which in our case now is (p +k)
2
. Also we have taken care
of the shift in the integration variable k
α
→k
α
−(uv +v) p
α
−vq
α
where due to
the contraction with p
α
p
β
only v
2
q
α
q
β
contributes.
For the
+
dk integral we get
d
4
k
(2π)
4
1
k
2
−vvQ
2
(1 −ωu)
3
=
−i
(4π)
2
1
Γ(3)
1
vvQ
2
(1 −ωu)
. (13)
The
+
dv integration gives
1
0
dvv
2
v(vv)
−1
=
1
2
, (14)
and therefore
I
1
(q, p) =
−i
(4π)
2
( p ·q)
2
Q
2
·
1
2
1
0
du
1
(1 −ωu)
. (15)
Exercise 5.13

342 5. Perturbative QCD I: Deep Inelastic Scattering
Exercise 5.13
Expanding
1
1 −ωu
=
∞
n=0
(ωu)
n
, (16)
we find, after trivial integration,
I
1
(q, p) =
−i
(4π)
2
( p ·q)
2
Q
2
1
2
∞
n=0
1
(n +1)
ω
n
. (17)
In the same way we can evaluate I
2
(q, p):
I
2
(q, p) =
d
4
k
(2π)
4
p ·(q +k) p ·k
(q +k)
2
(q +k + p)
2
(k + p)
2
=
d
4
k
(2π)
4
( p ·k) p ·(k −q)
k
2
(k + p)
2
(k + p −q)
2
=Γ(3)
1
0
du
1
0
dvv
d
4
k
(2π)
4
p ·(k −vq) p ·(k −(1 −v)q)
k
2
−vvQ
2
(1 +ωu)
3
, (18)
where we again copied from (5.269) and performed in addition to the changes
carried out in (12) the substitution q →−q,i.e.ω →−ω. Also the shift of the
integration variable now reads k → k −(u
v +v) p +vq.
I
2
therefore becomes
I
2
(q, p) =−Γ(3)( p ·q)
2
1
0
du
1
0
dvv
2
v
d
4
k
(2π)
4
1
k
2
−vvQ
2
(1 +ωu)
3
(19)
=
+i
(4π)
2
( p ·q)
2
Q
2
1
2
∞
n=0
1
(n +1)
(−ω)
n
, (20)
where we used (13) and obtained for the
+
dv integration
1
0
dvv
2
v(vv)
−1
=
1
2
. (21)
We also expanded
1
(1 +ωu)
=
∞
n=0
(−ωu)
n
. (22)
Let us now proceed to calculate I
3
(q, p), which is a little bit more tricky
since we deal with four propagators, two of which contain off-shell momenta

5.5 Calculation of the Wilson Coefficients 343
q
2
=−Q
2
= 0. To circumvent this problem we note the following relation:
1
(k + p)
2A
·
1
(k
2
)
B
=
Γ(A +B)
Γ(A)Γ(B)
1
0
du
u
A−1
u
B −1
(k +up)
2(A+B)
, (23)
which holds for arbitrary k
2
= 0and p
2
=0. It can be proven using Feynman
parameters:
1
(k + p)
2A
·
1
(k
2
)
B
=
Γ(A +B)
Γ(A)Γ(B)
1
0
du
u
A−1
u
B −1
u(k + p)
2
+uk
2
A+B
, (24)
where
u(k + p)
2
+uk
2
=k
2
+2ku p = (k +up)
2
completes the proof. Using
this twice, the integral I
3
(q, p) can be written as
I
3
(q, p) =
d
4
k
(2π)
4
p ·(q +k) k ·qp·k
(q +k)
2
(q +k + p)
2
(k + p)
2
k
2
=
1
0
du
1
0
dv
d
4
k
(2π)
4
p ·(q +k) k ·qp·k
(k +up)
4
(q +k +v p)
4
=Γ(4)
1
0
du
1
0
dv
1
0
dyy y
×
d
4
k
(2π)
4
p ·(q +k) p ·k (k −up) ·q
yk
2
+y(k +q +(v −u) p)
2
4
, (25)
where in the last step k → k −up is shifted and a third Feynman parameter is
introduced. The denominator can now be simplified in the usual way
yk
2
+y(k +q +(v −u) p)
2
=k
2
+2k ·( yq +(v −u)yp)
+y(q +(v −u) p)
2
=
k +yq +(v −u)yp)
2
+yy(q +(v −u) p
2
=k
2
+yy
q
2
+2q · p(v −u)
=k
2
−yyQ
2
[1 −ω(v −u)] (26)
The shift of the integration momenta k = k
−yp−(v −u)yp has to be
performed in a similar way in the numerator:
(q +k)
α
(k −up)
β
k
σ
p
α
q
β
p
σ
=(k
+yq)
α
(k
−yq −vyp−u yp)
β
(k
−yq)
σ
p
α
q
β
p
σ
=k
α
k
β
(−yq)
σ
+k
β
k
σ
(yq)
α
+yq
α
( yq +vyp+u yp)
β
yq
σ
p
α
q
β
p
σ
=
k
2
4
( p ·q)
2
[1 −2y]+yy( p ·q)
3
(vy +u y) +yy
2
( p ·q)
2
q
2
. (27)
Exercise 5.13

344 5. Perturbative QCD I: Deep Inelastic Scattering
Exercise 5.13
Here we used the fact that under integration, contributions like ∼ k
α
or
k
α
k
β
k
σ
vanish and that k
α
k
β
=
1
4
k
2
g
αβ
. (See our discussion on dimensional
regularization before.)
With that we are left with two k
integrations:
1
4
d
4
k
(2π)
4
k
2
k
2
−yyQ
2
(1 −ω(v −u))
4
=
−i
4(4π)
2
Γ(3)
Γ(2)Γ(4)
1
yyQ
2
(1 −ω(v −u))
=
−i
2(4π)
2
1
Γ(4)
1
yyQ
2
(1 −ω(v −u))
(28a)
and
d
4
k
(2π)
4
1
k
2
−yyQ
2
(1 −ω(v −u))
4
=
i
(4π)
2
Γ(2)
Γ(4)
yyQ
2
(1 −ω)(v −u)
2
. (28b)
Inserting everything in (25) and performing the trivial
+
dy integration we
get
I
3
(q, p) =
i
2(4π)
2
1
0
du
1
0
dv
#
( p ·q)
3
Q
4
(v +u)
[1 −ω(v −u)]
2
+
( p ·q)
2
Q
4
q
2
1
[1 −ω(v −u)]
2
&
=
i
4(4π)
2
1
0
du
1
0
dv
(v +u)ω −2
[1 −ω(v −u)]
2
( p ·q)
2
Q
2
. (29)
Expanding again in ω yields
1
[
1 −ω(v −u)
]
2
=
∞
n=0
Γ(n +2)
Γ(2)Γ(n +1)
(v −u)
n
ω
n
=
∞
n=0
(1 +n)(v −u)
n
ω
n
(30)
and the remaining integrations can be performed:
1
0
du
1
0
dv(v −u)
n
=
1
(1 +n)
1
0
du
(1 −u)
1+n
+(−)
n
u
1+n
=
1
(1 +n)(2 +n)
1 +(−)
n
, (31)

5.5 Calculation of the Wilson Coefficients 345
1
0
du
1
0
dv(v +u)(v −u)
n
=
1
0
du
'
u
n+2
n +2
−(−)
n
u
n+2
n +2
+2
u
u
n+1
(n +1)
−(−)
n+1
2u
n+2
n +1
(
=
1
(n +2)(n +3)
−
(−)
n
(n +2)(n +3)
+
2
(n +2)(n +3)(n +1)
−(−)
n+1
2
(n +1)(n +3)
. (32)
Inserting (30), (31), and (32) into (29) yields
I
3
(q, p)
=
)
i
4(4π)
2
∞
n=0
#
1 +n
(n +2)(n +3)
1 −(−)
n
+
2
(n +2)(n +3)
+
2(−)
n
(n +3)
&
ω
n+1
−
i
2(4π)
2
∞
n=0
1
(2 +n)
1 +(−)
n
ω
n
*
( p ·q)
2
Q
2
=
)
i
4(4π)
2
∞
n=0
#
2
(3 +n)
−
1
(2 +n)
1 −(−)
n
+2
1
(2 +n)
−
1
(3 +n)
+
2(−)
n
(n +3)
&
ω
n+1
−
i
2(4π)
2
∞
n=0
1
(2 +n)
1 +(−)
n
ω
n
*
( p ·q)
2
Q
2
=
)
i
4(4π)
2
∞
n=0
1
(2 +n)
ω
n+1
1 +(−)
n
−
i
2(4π)
2
∞
n=0
1
(2 +n)
1 +(−)
n
ω
n
*
( p ·q)
2
Q
2
=
⎧
⎨
⎩
i
2(4π)
2
∞
n=0,2,4,
1
(2 +n)
ω
n+1
−
i
(4π)
2
∞
n=0,2,4,
1
(2 +n)
ω
n
⎫
⎬
⎭
( p ·q)
2
Q
2
.
(33)
Taking into account the contribution coming from the exchange term
(q →−q), which in this case cancels odd powers of ω and doubles even powers,
we find
I
3
(q, p) + I
3
(−q, p) =
⎛
⎝
−2i
(4π)
2
∞
n=0,2,4,
1
(2 +n)
ω
n
⎞
⎠
( p ·q)
2
Q
2
. (34)
Exercise 5.13

346 5. Perturbative QCD I: Deep Inelastic Scattering
Exercise 5.13
To get the final answer we have to insert (34), (17), and (20), into (10), which
yields
p
µ
p
ν
T
(2)gg
µν
(direct) + p
µ
p
ν
T
(2)gg
µν
(exchange)
= 8g
2
iT
f
[
2I
1
(q, p) +2I
1
(−q, p) −2(I
2
(q, p)
+I
2
(−q, p) +I
3
(q, p) + I
3
(−q, p))
]
=
8
(4π)
2
g
2
T
f
n=0,2,4,
#
2
(n +1)
+
2
(n +1)
−
4
(n +2)
&
ω
n
( p ·q)
2
Q
2
=
32
(4π)
2
g
2
T
f
n=0,2,4,
1
(1 +n)(2 +n)
ω
n
( p ·q)
2
Q
2
. (35)
Finally we therefore get
˜
F
2
2x
=32
α
s
4π
T
f
·
∞
n=0,2,4,
1
(1 +n)(2 +n)
ω
n
. (36)
Repeating the steps we did after (5.277), and observing that
1
(1 +n)(2 +n)
=
1
(1 +n)
−
1
(2 +n)
=
1
0
dxx
n−1
x −
1
0
dxx
n−1
x
2
=
1
0
dxx
n−1
x(1 −x), (37)
the desired result emerges as
F
g
L
(x, Q
2
) = T
f
α
s
4π
16
1
x
dy
y
x
y
1 −
x
y
F
g
2
( y), (38)
which has been quoted in (5.282).
EXAMPLE
5.14 Calculation of Perturbative Corrections to Structure Functions
with the Cross-Section Method
We have calculated in the previous sections the Wilson coefficients in O(α
s
)
using operator product expansion and a dispersion relation (the optical theorem),
which relates the imaginary part of the forward scattering amplitude to the cross
section. Instead of looking at the imaginary part it is sometimes convenient to
calculate the cross section directly. This procedure is more general and has an

5.5 Calculation of the Wilson Coefficients 347
wider applicablity. We would like to demonstrate this method, which we call the
cross-section method, by essentially reproducing the results from the sections
before, i.e. the perturbative corrections to F
q
L
and F
g
L
.
Following (5.281) and (5.282), we can denote the structure function
F
L
(x, Q
2
) and F
2
(x, Q
2
) as
F
k
L
(x, Q
2
) =
1
x
dz
z
F
L,k
(z, Q
2
)F
k
2
x
z
, Q
2
, (1a)
F
k
2
(x, Q
2
) =
1
x
dz
z
F
2,k
(z, Q
2
)F
k
2
x
z
, Q
2
, (1b)
where the index k refers either to quarks q or gluons g.Asusual,Q
2
=−q
2
de-
scribes the momentum of the virtual photon. x = Q
2
/2Pq refers to the Bjorken
variable with respect to the nucleon state |P .Thevariablez = Q
2
/2pq,on
the other hand, corresponds to the Bjorken variable with respect to the parton
momentum p.
At leading order, F
(0)k
2
is the structure function related to the pure parton
density F
(0)q
2
= xq(x). F
L,k
and F
2,k
describe the radiative corrections to the
parton subprocess
k +γ
∗
→ X ,
which are illustrated in the Fig. 5.26.
In the language of operator product expansion, the distribution functions
xq(x) and xG(x) can be considered as the nonperturbative input parameters,
while F
L,k
and F
2,k
are the coefficient functions, calculable order by order in
perturbation theory. Then F
L,k
is related to scattering of a longitudially po-
larized virtual photon off parton k and F
2,k
to the scattering of a transversely
polarized photon. Since the variable z corresponds to the Bjorken variable with
respect to the parton momentum, the calligraphic structures F
2,k
and F
L,k
can
be interpreted as parton structure functions.
In the following calculation, all problems related to renormalization will be
neglected. Indeed, as we have seen before, in the special case we are interested
in, the quantity F
L,k
(x) is finite at O(α
s
). In general this function is diver-
gent and we have to use a renormalization prescription to remove poles like 1/ε
that arise when using dimensional regularization. However, for the projection
onto F
L
, poles do not arise. Therefore, we can carry out the calculation in d = 4
dimensions.
The parton structure functions can be obtained from the parton tensor, which
we can define as
W
µν
=
1
2
1
2π
l
dPS
(l)
M
µ
(l)M
∗
ν
(l) (2)
Example 5.14
