Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.


348 5. Perturbative QCD I: Deep Inelastic Scattering
Example 5.14
X = +
+++
+
γ *
k=q,g
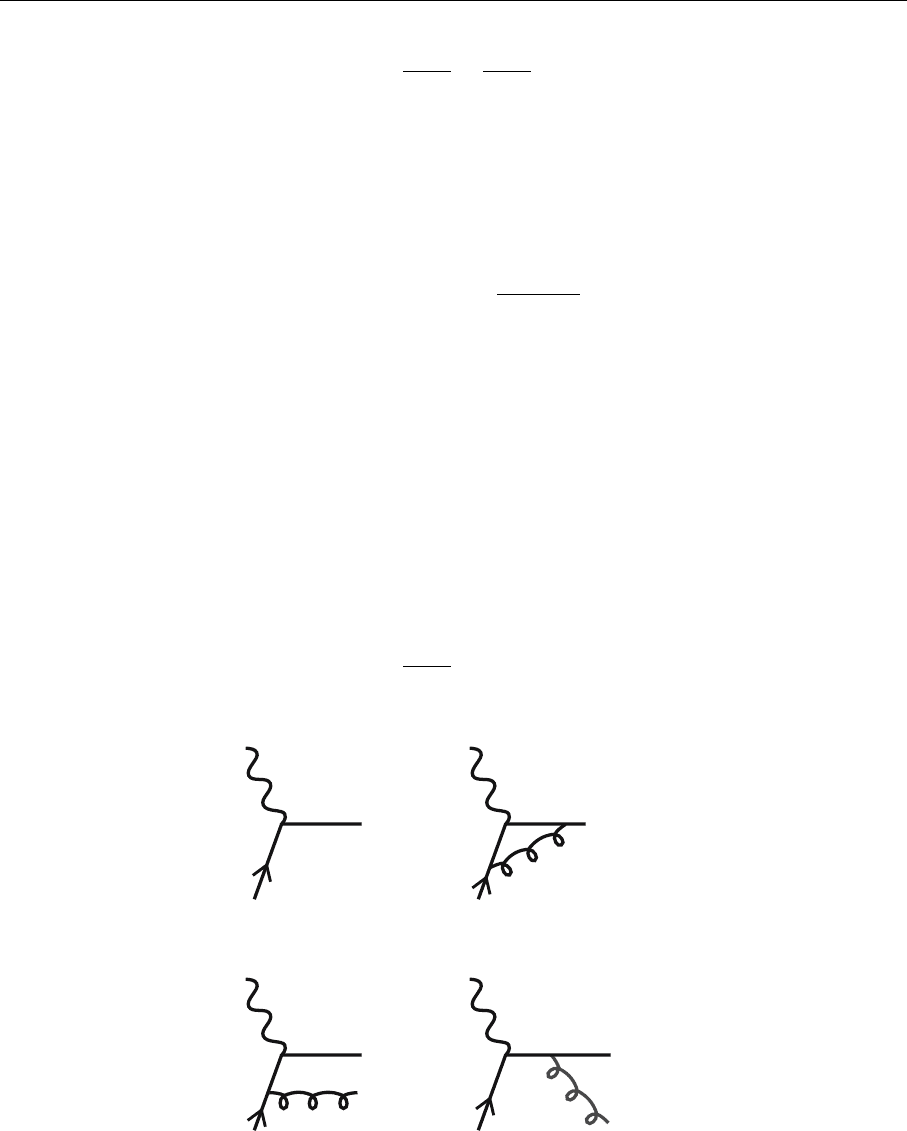
Fig. 5.26. Examples of deep
inelastic lepton–parton (k +
γ
∗
→ X) subprocesses
with
dPS
(l)
=
⎛
⎝
l
;
j=1
d
3
p
j
(2π)
3
2p
0
⎞
⎠
(2π)
4
δ
⎛
⎝
p +q −
l
j=1
p
j
⎞
⎠
=
⎛
⎝
l
;
j=1
d
4
p
j
(2π)
3
δ( p
2
j
)Θ( p
0
)
⎞
⎠
(2π)
4
δ
⎛
⎝
p +q −
l
j=1
p
j
⎞
⎠
, (3)
and M
µ
(l) denotes the amplitude for the photon–parton reaction
γ
∗
+ p −→ p
1
+ p
2
+···+p
l
. (4)
Here p stands for the incoming parton and p
1
···p
l
for the partons produced
in the scattering reaction. The integral
+
dPS
(l)
is just the Lorentz invariant
phase space for on-shell particles p
2
j
=0. Remember that d
3
p/(2π)
3
2p
0
is the
Lorentz-invariant measure. Note that we have averaged over all spins in the ini-
tial state. The parton structure tensor can again be decomposed as in the general
case in (5.249) in terms of F
L
and F
2
W
µν
=
g
µν
−
q
µ
q
ν
q
2
F
L
+
p
µ
p
ν
−
p ·q
q
2
p
µ
q
ν
+ p
ν
q
µ
+g
µν
( p ·q)
2
q
2
F
2
p ·q
, (5)

5.5 Calculation of the Wilson Coefficients 349
with the corresponding projection onto F
L
F
L
=
Q
2
( p ·q)
2
p
µ
p
ν
W
µν
. (6)
To check wether our normalization is correct we first calculate the zeroth
order, i.e. the tree-level contribution which is the first diagram on the right-hand
side of the pictorial equation in Fig. 5.26, i.e. the contribution without additional
gluons.
Inserting the tree-level amplitude
M
µ
(1) = u( p, s)γ
µ
u(p
1
, s
1
) (7)
into (2) yields
W
µν
=
1
4π
d
4
p
1
(2π)
3
δ( p
2
1
)Θ( p
0
)(2π)
4
δ( p +q − p
1
)tr
γ
µ
p/γ
ν
p/
1
.
When projecting onto F
2
with −g
µν
/2 (see (5.252); the p
µ
p
ν
term of the
projector does not contribute!) we get
−g
µν
2
W
µν
=
1
2
δ
( p +q)
2
Θ( p
0
)4p ·q
= δ
Q
2
z
(1 −z)
Q
2
z
=δ(1 −z) = F
2
(z), (8)
wherewehaveusedp
2
= 0and2p ·q/Q
2
=1/z. This result has an obvious in-
terpretation and – if inserted into (1) – shows that at zeroth order the structure
function is equal to the bare parton density
F
q
2
(x) = F
(0)q
2
(x) = xq(x), (9)
as it must be. To obtain the corresponding first-order corrections to F
L
we have
to analyze the diagrams shown in Fig. 5.27.
This requires the evaluation of the real-gluon emission graphs (c) and (d)
and also the interference of the lowest-order graph (a) with the virtual gluon
exchange graph (b). Due to the equations of motion
p/u( p) =
u(p) p/ =0 , (10)
only diagram (c) contributes to F
L
. All other diagrams vanish under the projec-
tion (6). The real gluon emission graphs describe the reaction
γ
∗
(q) +q( p) −→ q( p
) +G(k),
where the symbols in brackets are the momenta carried by the corresponding
particles.
Note that the letter q in γ
∗
(q) denotes the four-momentum of the pho-
ton while q( p) denotes a quark with four-momentum p. To calculate the cross
section we must evaluate the two-particle phase space
Example 5.14
350 5. Perturbative QCD I: Deep Inelastic Scattering
Example 5.14
+
+
a)
b)
c) d)
Fig. 5.27. Diagrams giv-
ing the correction of order
O(α
s
) to the pointlike quark–
photon cross section. The
interference term of |a +b|
2
give rise to a contribution of
order O(α
s
).ForF
L
with the
projection p
µ
p
ν
and p
2
=0
only diagram (c) gives a
nonzero contribution
dPS
(2)
=
d
4
p
(2π)
3
d
4
k
(2π)
3
(2π)
4
δ( p +q − p
−k)δ
+
( p
2
)δ
+
(k
2
),
(11)
where we introduced the shorthand notation δ
+
( p
2
) = δ( p
2
)Θ( p
0
).
We will work in the centre-of-mass system (CMS) of the parton and vir-
tual photon. The incoming momenta are directed along the z direction. Thus the
kinematics is given by
p = (|p|, 0, 0, |p|),
q = (q
0
, 0, 0, −|p|) =
|p|
2
−Q
2
, 0, 0, −|p|
. (12)
The momenta of the produced particles are denoted as
k =
(
|k|, 0, |k|sinΘ, |k|cosΘ
)
,
p
=
(
|k|, 0, −|k|sinΘ, −|k|cosΘ
)
, (13)
so that k+ p
= 0andk
2
= p
2
=0. For later use we will also introduce the
Mandelstam variables
s = ( p +q)
2
, t = ( p −k)
2
, u = ( p − p
)
2
. (14)
The phase space then can be written as
dPS
(2)
=
d
4
k
(2π)
2
δ
+
(k
2
)δ
+
( p +q −k)
2
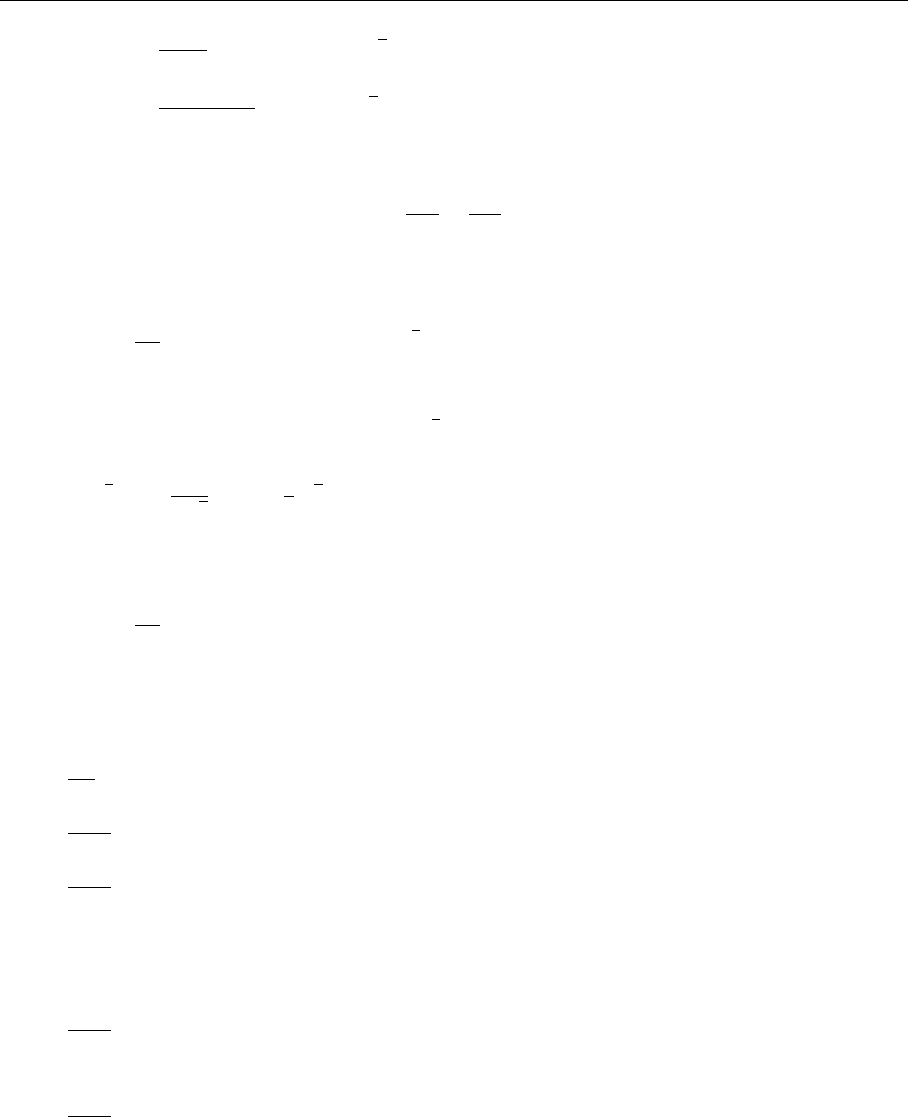
5.5 Calculation of the Wilson Coefficients 351
=
d
4
k
(2π)
2
δ
+
(k
2
)δ
+
(s −2|k|
√
s)
=
d
3
k
(2π)
2
(2|k|)
δ
+
(s −2|k|
√
s), (15)
where
dk
0
δ
+
(k
2
) =
dk
0
δ(k
02
−|k|
2
)Θ(k
0
) =
1
2|k|
=
1
2|k |
. (16)
has been used. Performing the trivial φ integration yields
dPS
(2)
=
1
4π
∞
0
d|k ||k|
1
−1
dcosΘδ(s −2
√
s|k|). (17)
To proceed, let us introduce the variable y =
1
2
(1 +cos Θ) and write the
δ function as
δ(s −2
√
s|k|) =
1
2
√
s
δ
|k|−
1
2
√
s
(18)
so that the simple expression
dPS
(2)
=
1
8π
1
0
dy (19)
is obtained. Now we write the Mandelstam variables s, t, u (14) in terms of the
variables Q
2
, y,andz = Q
2
/2p ·q and find
s =
Q
2
z
(1 −z),
t =
−Q
2
z
(1 − y),
u =
−Q
2
z
y . (20)
The last two equations are obtained by recognizing that in the CMS
t = ( p −k)
2
=−2p ·k =−2|p||k|(1 −cosΘ) =−p ·q(1 −cosΘ)
=
−Q
2
z
(1 − y),
u = ( p − p
)
2
=−2p · p
=−2|p||k|(1 +cosΘ) =−p ·q(1 +cosΘ)
=
−Q
2
z
y , (21)
Example 5.14
352 5. Perturbative QCD I: Deep Inelastic Scattering
Example 5.14
with z = Q
2
/2p ·q. Twice we have used here that in the CMS
p ·q = p
0
q
0
− pq =|p|q
0
+|p||p|=|p|
q
0
+ p
0
=|p|(2|k|). (22)
With these preliminaries we have everything at hand to calculate the real
gluon emission process. For the amplitude in (c) of the last figure we write
M
µ
= gu
a
( p
, s
)γ
µ
i
p/ −k/
γ
α
λ
A
ab
2
u
b
( p, s)ε
∗α
, (23)
so that we get for the spin-summed matrix element
s
,s,ε
M
µ
(2)M
∗
ν
(2)
= g
2
C
F
s
,s,ε
u(p
, s
)γ
µ
1
p/ −k/
γ
α
u(p, s)u( p, s)γ
β
1
p/ −k/
γ
ν
u(p
, s
)ε
∗α
ε
β
= g
2
C
F
tr
p/
γ
µ
( p/ −k/)γ
α
p/γ
β
( p/ −k/)γ
ν
−g
αβ
( p −k)
4
(24)
where the color factor is
1
N
a,b
A,B
λ
A
ab
2
λ
B
ba
2
δ
AB
=
N
2
−1
2N
=C
F
=
4
3
(25)
and the sum over gluon polarisation in the Feynman gauge
ε
ε
∗α
ε
β
=−g
αβ
. (26)
Projecting onto F
L
with p
µ
p
ν
we find
p
µ
p
ν
spins
M
µ
(2)M
∗
ν
(2) =
g
2
C
F
( p −k)
4
·2tr
p/
p/k/ p/k/ p/
=
g
2
C
F
( p −k)
4
·8(p ·k)
2
tr
p/
p/
=
−4g
2
C
F
( p −k)
4
(−2p ·k)
2
(−2p
· p)
=
−4g
2
C
F
z
2
z
2
u =−4g
2
C
F
u =+4g
2
C
F
Q
2
z
y .
(27)
In the last step we inserted the Mandelstam variables according to (20).
Inserting (27) and (19) into (2) yields
p
µ
p
ν
W
µν
=
1
8π
2
g
2
C
F
Q
2
z
1
0
dyy
=
1
16π
2
g
2
C
F
Q
2
z
. (28)

5.5 Calculation of the Wilson Coefficients 353
Using (6)
F
L
=
Q
2
( pq)
2
p
µ
p
ν
W
µν
=
4z
2
Q
2
p
µ
p
ν
W
µν
(29)
gives
F
L
=
g
2
4π
2
C
F
·z = 4C
F
α
s
4π
·z , (30)
and inserting that into (1) brings us finally to
F
q
L
(x, Q
2
) = 4C
F
α
s
4π
1
x
dz
z
zF
q0
2
x
z
, Q
2
=4C
F
α
s
4π
1
x
dy
y
x
y
F
q0
2
y, Q
2
. (31)
This confirms by use of a completely different method our former result of
(5.281). The confirmation of the gluon contribution F
g
L
will be left to Excer-
cise 5.14.
Here we have presented a calculation of the α
s
correction to F
L
which ap-
parently is much simpler than the more formal calculation we did before. Also it
might appeal to the physical intuition to calculate directly the cross section and
stay as close as possible to the parton model in each step of the calculation.
The calculations of the corrections to F
2
may be found in the work of
G. Altarelli at al.
19
The complete 2-loop corrections were calculated by Zijlstra
and van Neerven.
20
However, the cross-section method becomes increasingly
difficult with 3-particle phase space integrals and, at least in the near future,
calculations of 3-loop corrections do not seem to be feasible.
Finally, it is worthwhile to mention that 3-loop corrections are already avail-
able for the first 10 moments of F
L
and F
2
with the operator product expansion
method.
21
19
G. Altarelli, R.K. Ellis, G. Martinelli: Nucl. Phys. B 157, 461 (1979).
20
E.B. Zijlstra and W.L. van Neerven: Nucl. Phys. B 383, 525 (1992) 525.
21
S.A. Larin, P. Nogueira, T. van Ritbergen and J.A.M. Vermaseren:
Nucl. Phys. B 492, 338 (1997).
Example 5.14
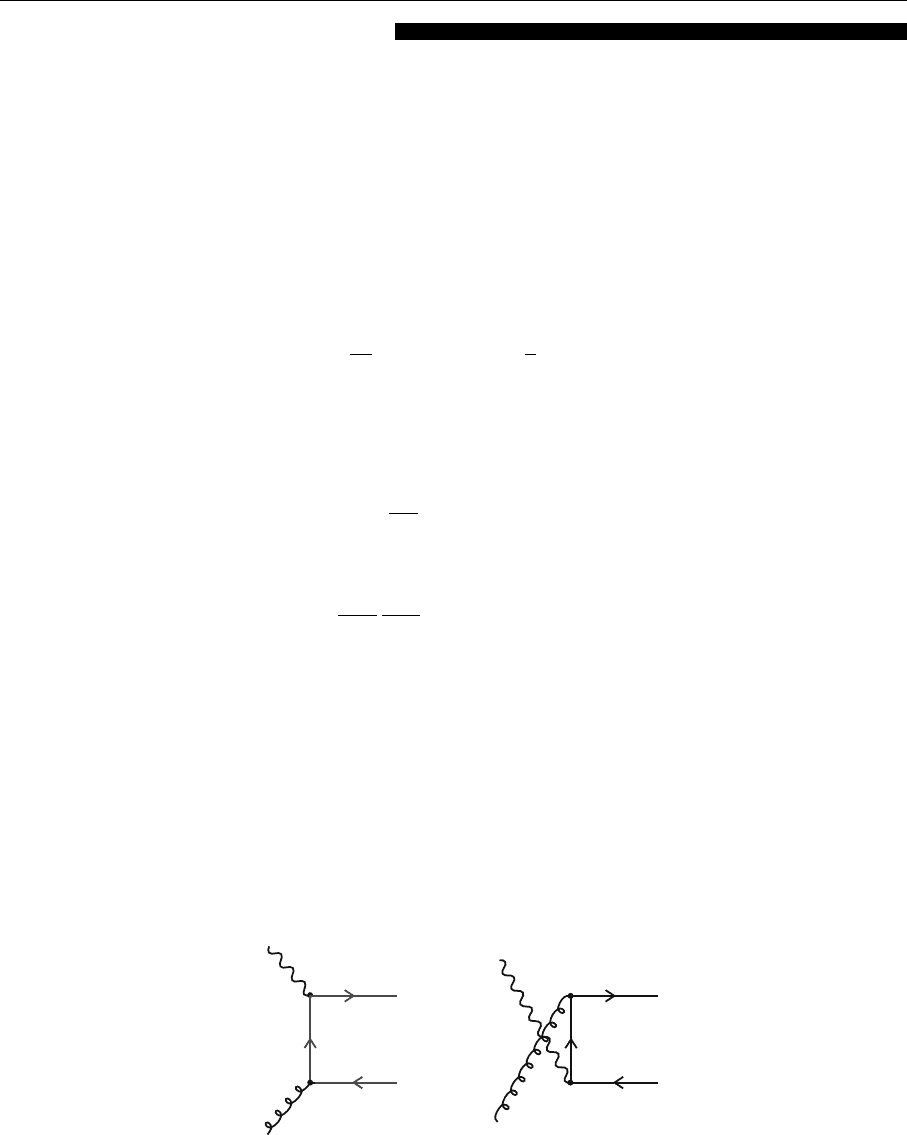
354 5. Perturbative QCD I: Deep Inelastic Scattering
q
q
p
p
kk
p' p'
+
Fig. 5.28. Diagrams con-
tributing to order α
s
to
photon–gluon scattering. The
wavy line represents the vir-
tual photon, the curled line
the gluon
EXERCISE
5.15 Calculation of the Gluonic Contribution to F
L
with the Cross-Section Method
Problem. Calculate the contribution of photon–gluon scattering to the lon-
gitudinal structure function. Use the cross-section method as in the previous
example 5.14.
Solution. The necessary diagrams we encounter are shown in the Fig. 5.28.
Let us first collect the necessary definitions from Examples 5.13 and 5.14.
The gluonic structure function is given by a convolution
F
g
L
=
1
x
dz
z
F
L
(z, Q
2
)F
(0)g
2
x
z
, Q
2
(1)
with a function F
L
(z, Q
2
) calculable in perturbation theory and the gluon dens-
ity F
(0)g
2
(x, Q
2
) = xG(x, Q
2
). We calculate F
L
by projecting onto the partonic
scattering tensor W
µν
(see (6) and (29) of Example 5.14):
F
L
(z, Q
2
) =
4z
2
Q
2
p
µ
p
ν
W
µν
, (2)
where the partonic scattering tensor to the order we are working is given by
W
µν
=
1
(4π)
1
(8π)
1
0
dyM
µ
(2)M
∗
ν
(2), (3)
where we have used the representation (2) and (19) from Example 5.14 for the
two-particle phase space (l = 2). The kinematics are the same as previously; i.e.
for the reaction
g(p) +γ
∗
( p) →
¯
q(k) +q( p
) (4)
we choose
p = (|p|, 0, 0, |p|),
k = (|k|, 0, |k |sin θ, |k|cos Θ) ,
p
=(|k|, 0, −|k|sin θ, −|k|cos Θ) , (5)

5.5 Calculation of the Wilson Coefficients 355
and define the Mandelstam variables as
s = ( p +q)
2
=
Q
2
z
(1 −z),
t = ( p −k)
2
=
−Q
2
z
(1 − y),
u = ( p − p
)
2
=
−Q
2
z
y , (6)
with y =
1
2
(1 +cos Θ). Remember also that p
2
= p
2
= 0 =k
2
, q
2
=−Q
2
and
that the Bjorken variable with respect to the parton momentum p is defined
as z = Q
2
/2p ·q. With these definitions the calculation is straightforward. The
amplitude of the process reads
M
µ
(2) = g
'
¯
u
a
( p
)γ
µ
i
p/ −k/
λ
A
ab
2
γ
α
u
b
(k)
+
¯
u
α
( p
)γ
α
λ
A
ab
2
i
q/ −k/
γ
µ
u
b
(k)
(
·ε
α
. (7)
When squaring we find for the color sum
1
N
2
−1
A,B,a,b
λ
A
ab
2
λ
A
ba
2
=
1
N
2
−1
A,B
tr
λ
A
2
λ
A
2
=
1
N
2
−1
A,B
1
2
δ
AB
=
1
2
.
(8)
Together with the sum over quark flavors this gives a factor T
f
=
1
2
N
f
. With
p
− p = q −k the squared amplitude becomes
p
µ
p
ν
spins
M
µ
(2)M
∗
ν
(2)
=T
f
g
2
#
tr
p/( p/ −k/)γ
α
k/γ
β
( p/ −k/) p/ p/
·
1
( p −k)
4
+tr
γ
α
( p/
− p/) p/k/ p/( p/
− p/)γ
β
p/
·
1
( p − p
)
4
(9)
+tr
p/( p/ −k/)γ
α
k/ p/(p/
− p/)γ
β
p/
1
( p − p
)
2
( p −k)
2
+tr
γ
α
( p/
− p/) p/k/γ
β
( p/ −k/) p/ p/
1
( p − p
)
2
( p −k)
2
&
−g
αβ
= T
f
g
2
2
#
tr
p/k/k/k/ p/ p/
·
1
t
2
tr
p/
k/ p/p/
p/
·
1
u
2
−tr
p/k/ p/
p/k/ p/
·
1
ut
−tr
k/ p/p/
k/ p/p/
·
1
ut
&
. (10)
Exercise 5.15

356 5. Perturbative QCD I: Deep Inelastic Scattering
Exercise 5.15
The first two traces vanish due to k
2
= p
2
=0 and the second two are identical
because tr
γ
α
γ
β
...γ
γ
σ
= tr
γ
σ
γ
...γ
β
γ
α
. The remaining two traces give
−tr
p/k/ p/
p/k/ p/
=tr
p/k/ p/
k/ p/p/
=(2p · p
)(2p
·k) ·tr
[
p/k/
]
=2u ·t(2 p
·k) = 2u ·t ·s . (11)
What remains is therefore
p
µ
p
ν
spins
M
µ
(2)M
∗
ν
(2) = T
f
g
2
·8s = 8
Q
2
z
(1 −z)T
f
g
2
. (12)
Inserting this into (2) we finally find
F
L
(x, Q
2
) =
g
2
π
T
f
z(1 −z)
=16
α
s
4π
T
f
z(1 −z), (13)
which inserted into (1) gives the final answer
F
g
L
(x, Q
2
) = 16
α
s
4π
T
f
1
x
dz
z
[
z(1 −z)
]
F
(0)g
2
x
z
, Q
2
=16
α
s
4π
T
f
1
x
dy
y
x
y
1 −
x
y
F
(0)g
2
( y, Q
2
), (14)
which is completely in agreement with our previous result in (5.282).
5.6 The Spin-Dependent Structure Functions
In recent years it has become possible to measure, in addition to the struc-
ture functions F
1
(x, Q
2
) and F
2
(x, Q
2
), the so-called spin-dependent structure
functions g
1
(x, Q
2
) and g
2
(x, Q
2
). The spin-dependent structure functions play
a role only when the scattered leptons and hadrons are polarized. The origin of
these additional structure functions is quite obvious. For a polarized hadron, e.g.,
a proton, there is an additional Lorentz vector available, namely the spin vec-
tor s
µ
. Accordingly (3.6) has to be extended by some additional terms. Repeating
the analysis of Chap. 3 with the additional spin vector, we are led to the following
5.6 The Spin-Dependent Structure Functions 357
form of the scattering tensor:
W
µν
=
−g
µν
+
q
µ
q
ν
q
2
W
1
(x, Q
2
)
+
P
µ
−q
µ
q · P
q
2
P
ν
−q
ν
q · P
q
2
W
2
(x, Q
2
)
M
2
+iε
µνλσ
q
λ
s
σ
MG
1
(x, Q
2
)
+iε
µνλσ
q
λ
(s
σ
q · P −P
σ
q ·s)
G
2
(x, Q
2
)
M
. (5.285)
This equation is obviously an extension of (3.18). The factor i guarantees that
the transition current is real (the relation Γ
∗
µ
( p ↔ p
) = Γ
µ
must hold; see Ex-
ercise 3.3), while the ε tensor ensures that q
µ
W
µν
=q
ν
W
µν
=0 holds. Since
the additional contributions change their sign when the hadron spin direction is
reversed, they cancel upon spin-averaging. Thus only spin-independent struc-
ture functions can be measured with an unpolarized target. Analogously to the
unpolarized case, dimensionless functions are introduced according to
MG
1
(x, Q
2
) =
g
1
(x, Q
2
)
P ·q
,
G
2
(x, Q
2
)
M
=
g
2
(x, Q
2
)
(P ·q)
2
. (5.286)
This choice is motivated by the fact that g
1
has a simple interpretation in terms
of parton distributions and g
2
(x) thus occurs on the same footing as g
1
(x).The
additional spin-dependent contributions to the hadron scattering tensor are an-
tisymmetric; thus they cannot contribute when contracted with the symmetric,
unpolarized lepton tensor of (3.20). In order to measure polarized structure func-
tions in deep inelastic scattering, the lepton must also be polarized. The resulting
leptonic scattering tensor is
L
µν
=
1
4
tr[( p/ +m)(1 −s/
e
γ
5
)γ
µ
( p/
+m)γ
ν
]
=
1
4
[p
µ
p
ν
+ p
ν
p
µ
−g
µν
( p · p
−m
2
)]
−
m
4
tr( p/s/
e
γ
5
γ
µ
γ
ν
) −
m
4
tr(s/
e
γ
5
γ
µ
p/
γ
ν
)
=
1
4
[p
µ
p
ν
+ p
ν
p
µ
−g
µν
( p · p
−m
2
)]+imε
µναβ
q
α
s
β
e
, (5.287)
where
1
2
(1 −s/γ
5
) is the standard spin projection operator, and s
β
e
the spin vector
of the electron. Thus the polarized lepton tensor also contains an antisymmetric
part. Contracting both, we obtain the additional term
L
µν
W
µν
=···−2mM(g
λα
g
σβ
−g
λβ
g
σα
)q
λ
s
σ
p
q
α
s
β
e
G
1
−
m
M
(g
λα
g
σβ
−g
λβ
g
σα
)q
λ
(q · Ps
σ
p
−q ·s
p
P
σ
)q
α
s
β
e
G
2
. (5.288)
This poses the question of what choice of the polarization of electron and hadron,
i.e., nucleon, is most suitable. The relevant vectors in the centre-of-momentum
