Greiner W., Schrammm S., Stein E. Quantum Chromodynamics

Подождите немного. Документ загружается.

480 7. Nonperturbative QCD

where R is the distance between quark and antiquark. For simplicity, we do

not consider the color matrix structure of the ﬁelds in the following argument.

This does not change any results discussed here. We determine the quark–gluon

interaction term

= A

(7.163)

since the quarks are static.  is just the color charge density, which reads

(x) = δ

(3)

(x) −δ

(3)

(x −R), (7.164)

where the positive charge sits at site x = 0 and the antiquark is put on a lattice

site with distance R =|R|. The action per time generated by this interaction is

=−i

x(x)A

(x) =−i

x(x)A

(x)

=−i

(

(0) − A

(R)

)

. (7.165)

As this result is time-independent, we can write

=−i

⎡

⎣

dτ



(0,τ)− A

(R,τ)



⎤

⎦

. (7.166)

If we assume that the time interval T is much larger than the distance |R|between

the quarks we can approximate S

by a closed-loop integration on the lattice:

T 

≈−i

⎡

⎣

dτA

(0,τ)+

x=R

x=0

dsA( s, T )

dτA

(R,τ)+

x=0

x=R

dsA( s, 0)

⎤

⎦

=−i

(x)

=T ·V(R). (7.167)

Now, looking back to our discussion of Wilson loops, a rectangular loop with

sides R and T (see Fig. 7.8)

w(R, T ) =tr

[

...U

]

(7.168)

is just the product of the link variables around the contour l. That is, in the

continuum limit we have

w(R, T )=

−ig

(x)

= e

−T ·V(R)

, (7.169)

7.1 Lattice QCD Calculations 481

Fig. 7.8. The Wilson loop

to calculate the quark poten-

tial. A quark–antiquark pair

or their color ﬁelds, propa-

gate along the time links

where we have averaged over all possible gluonic conﬁgurations. As we dis-

cussed in the beginning, the assumption is that for large distances the potential

between quark and antiquark behaves like V

=σr.Fromthatweget

R large,T Ra

=−

lnw(R, T ) . (7.170)

In general the potential is similarly given by

V(R ) =−

lnw(R, T ) . (7.171)

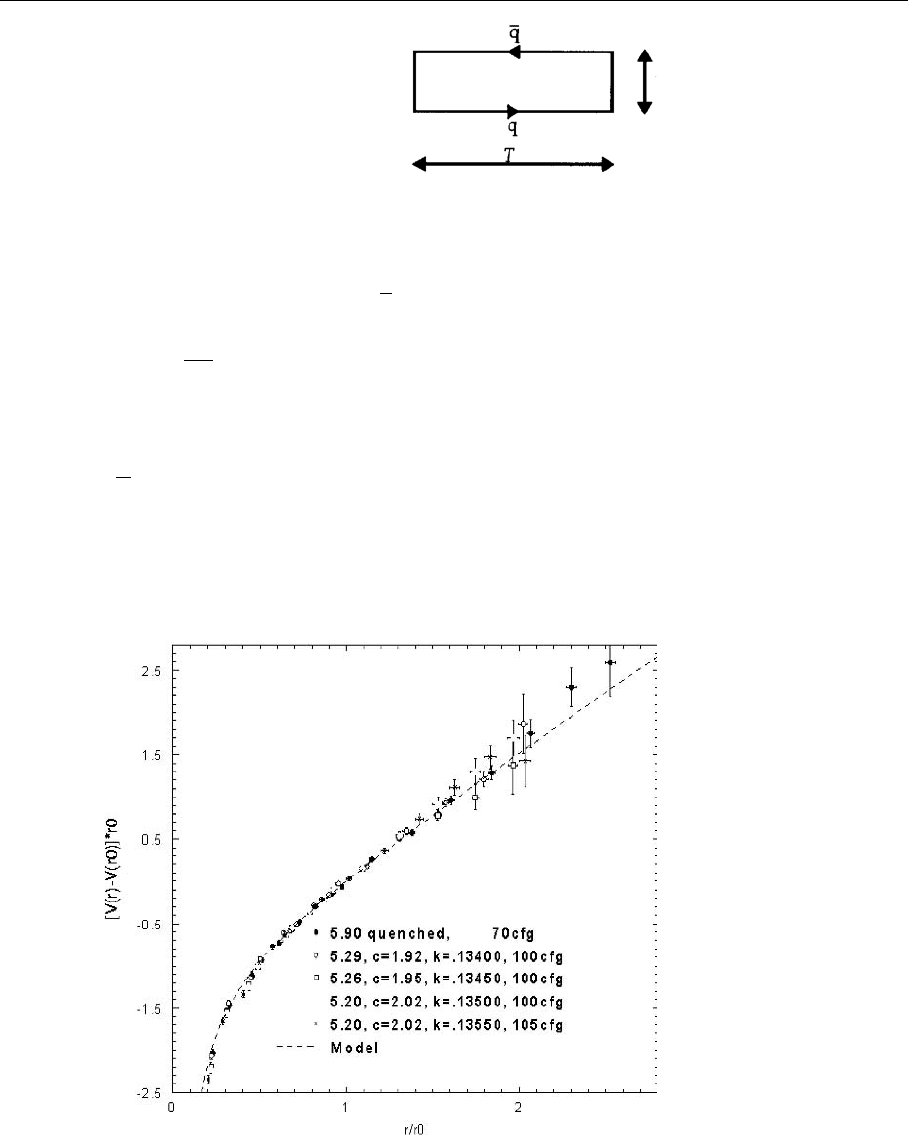
Figure 7.9 shows the results of a lattice calculation of the potential. One

clearly recognizes the linear slope of the potential at large R. In fact, the total

Fig. 7.9. Lattice calcula-

tion of the quark–antiquark

potential. One can clearly

see the linearly rising po-

tential indicating conﬁne-

ment (from: J. Garden et

al. (UKQCD collaboration):

Nucl. Phys. Proc. Suppl. 83,

165 (2000))

482 7. Nonperturbative QCD

potential can be ﬁtted by the expression

V(R ) =−

+σr . (7.172)

Another related method to determine the string tension from the value of the

Wilson loops is to determine the so-called Creutz ratio Cr of loops:

Cr ∼ σ =−ln



w(R, T )w(R −1, T −1)

w(R, T −1)w(R −1, T )



. (7.173)

One can easily check that (7.173) will reduce to the value of the string tension

in the limit of large R and T :

Cr ∼−ln

−σRT−σ(R−1)(T −1)

−σR(T −1)−σ(R−1)T

(

=−ln

−σ(2RT−R−T +1)

−σ(2RT−R−T )

(

=−ln



−σ



= σ. (7.174)

The advantage of this expression is that ﬁnite-size effects due to the usually

rather small values of R , T in a realistic calculation can be suppressed by taking

ratios of observables.

7.1.16 The Lattice at Finite Temperature

One of the major research topics for lattice calculations, especially of QCD, is to

study strong interactions at ﬁnite temperatures (“ﬁnite” means larger than zero

here).

As we have discussed in the introduction to the path-integral formalism

(Sect. 7.1.1), a transition from real to imaginary time, i.e. an analytical contin-

uation into the complex t-plane, led us directly to the partition function of the

theory

Z(T, V ) = N

[dφ

]φ

−βH

|φ

 , (7.175)

where the initial and ﬁnal states are identical.

In order to study vacuum properties one adopts the limit β →∞(or at least

very large in actual numerical calculations). It is now straightforward to study

ﬁnite temperatures within the same formalism. We just take a ﬁnite value of β =

1/T .

For imaginary times τ = it the time evolution operator and the Boltzmann

factor look alike

−iH(−iτ)

= e

−Hτ

←→ e

−βH

. (7.176)

M. Creutz: Phys. Rev. D 21, 2308 (1980).

7.1 Lattice QCD Calculations 483

This means that (7.175) can be seen as a transition amplitude for some ﬁnite time

interval T = 1/β. A ﬁnite extension in time together with periodic boundary

conditions has the consequence that the possible energy values ω

are discrete:

iω

= e

iω

−→ ω

2π

n , n = 0, 1,... . (7.177)

The ω

are the Matsubara frequencies, which are commonly used in ﬁnite-

temperature quantum ﬁeld theory. Note that so far our discussion has not relied

on any lattice discretization and is also valid for the continuum theory.

For fermions there is the difference that one must assume antiperiodic

boundary conditions due to their anticommutation properties:

iω

=−e

iω

−→ ω

2π

n +

n = 0, 1,... (7.178)

N.B. As we have just discussed, the temperature of the system is equal to the

inverse length of the system in time direction. When one performs a lattice calcu-

lation the lattice necessarily has a ﬁnite size in the time direction due to the lack

of inﬁnite computer power. This means there is always a temperature larger than

zero in every lattice calculation. So one has to ensure the temperature is kept low

enough by taking a big lattice so that the energy is much lower than the energy

of excited modes in the system.

In studies of ﬁnite-temperature properties of QCD matter, the values of the

energy density " and the pressure density P are of central importance. Let us

therefore outline how to determine " and P on the lattice.

Using the partition function Z we have

" =

∂

∂T

(

lnZ

)

V =const

P = T

∂

∂V

(

lnZ

)

T =const

. (7.179)

We see from these equations that we have to treat space and time separately in

order to keep V constant and vary T and vice versa.

There are actually two possibilities to vary T , for instance, as we discussed,

the temperature is given by the temporal extent L

of the lattice:

T =

, (7.180)

where N

is the number of points of the lattice in time direction. One can either

vary T by changing the lattice spacing a, or one could keep a but change the

number of points in the time direction. The latter method has the advantage that

it would change T without altering the volume of the system V = (N

,which

is just what one needs in (7.179). There is a major disadvantage, however. N

W. Greiner, H. Stöcker, L. Neise: Thermodynamics and Statistical Mechanics

(Springer Berlin, Heidelberg 1995).

484 7. Nonperturbative QCD

an integer (in addition many lattice gauge codes require even values of N

), so

that the variation possibilities of temperature

−

+1)a

≈

)

(7.181)

is rather coarse. Therefore it is customary to stick with the former approach,

varying a. This one has its own problem since the volume would change too with

changing scale parameter. So we formally have to introduce two scales a

, a

for

the space and time directions (this is only needed to perform the derivatives; af-

terwards one can set a

=a again). In this case one has to rewrite the Wilson

action (7.48) (including only gluons here):





1 −

Re trP



+rβ





1 −

Re trP



, (7.182)

where P

are plaquettes which lie in a plane with constant time, i.e. the (xy),

(xz),or(yz ) planes, whereas P

contains links in the time direction ((xt), (yt),

(zt) planes).

and β

are the inverse coupling strength deﬁned via

, r )

, (7.183)

where the anisotropy factor is given by r =a

The spatial and temporal coupling constants g

, g

generally depend on the

coupling g

, assuming an isotropic lattice r = 1, and the anisotropy in some com-

plicated fashion. In the isotropic limit r =1wehaveg

, 1) = g

The factors r and 1/r can be intuitively explained by considering the follow-

ing argument. The volume element of the action a

becomes a

−1

.The

spacelike part of the action is not further modiﬁed. The space–time plaquettes

contain two links in the time direction U

∼ e

i A

. For small lattice spacing

1 −U is proportional to a

compared to a

for spacelike links, altogether there is

an additional factor of r

for the contributions from P

. Neglecting corrections

arising from g

= g

for r = 1, we now have the following expression for the

action:

S ∼rS

+corrections , (7.184)

where S

and S

contain space–time plaquettes P

or space–space plaquettes P

respectively.

Using this result, we can return to calculate the energy and pressure of the

system. For the energy we get, using (7.179) and T = 1/(N

) =r/(N

" =

∂

∂r

ln Z(r)



r=1

. (7.185)

7.1 Lattice QCD Calculations 485

Fig. 7.10. Energy dens-

ity and pressure in a lat-

tice calculation including

the fermion determinant (for

2 flavors). The graph is

taken from C. Bernard et al.

(MILC collaboration): Nucl.

Phys. Proc. Suppl. 53, 442

(1997)

Using the deﬁnition of Z and the expression for the action (7.184) we get the

result

" =

−

∂S

∂r



r=1

S

−S

+"

(7.186)

with



∂β

∂r

∂β

∂r





r=1

, (7.187)

where "

is the contribution to the energy arising from the dependence of the

coupling on a scale change, i.e. quantum corrections.

In Fig. 7.10 the results of a calculation of the energy and pressure on the lat-

tice as a function of temperature are shown. One can see a clear dramatic rise

in the energy density at a temperature of about 150 MeV, signaling a transition

from hadronic QCD states to a gaslike state, the experimentally much sought-

after quark–gluon plasma (QGP).

7.1.17 The Quark Condensate

Another order parameter which signals the phase transition is the quark conden-

sate 

qq.Nowqq = q

, where we have introduced the left-handed

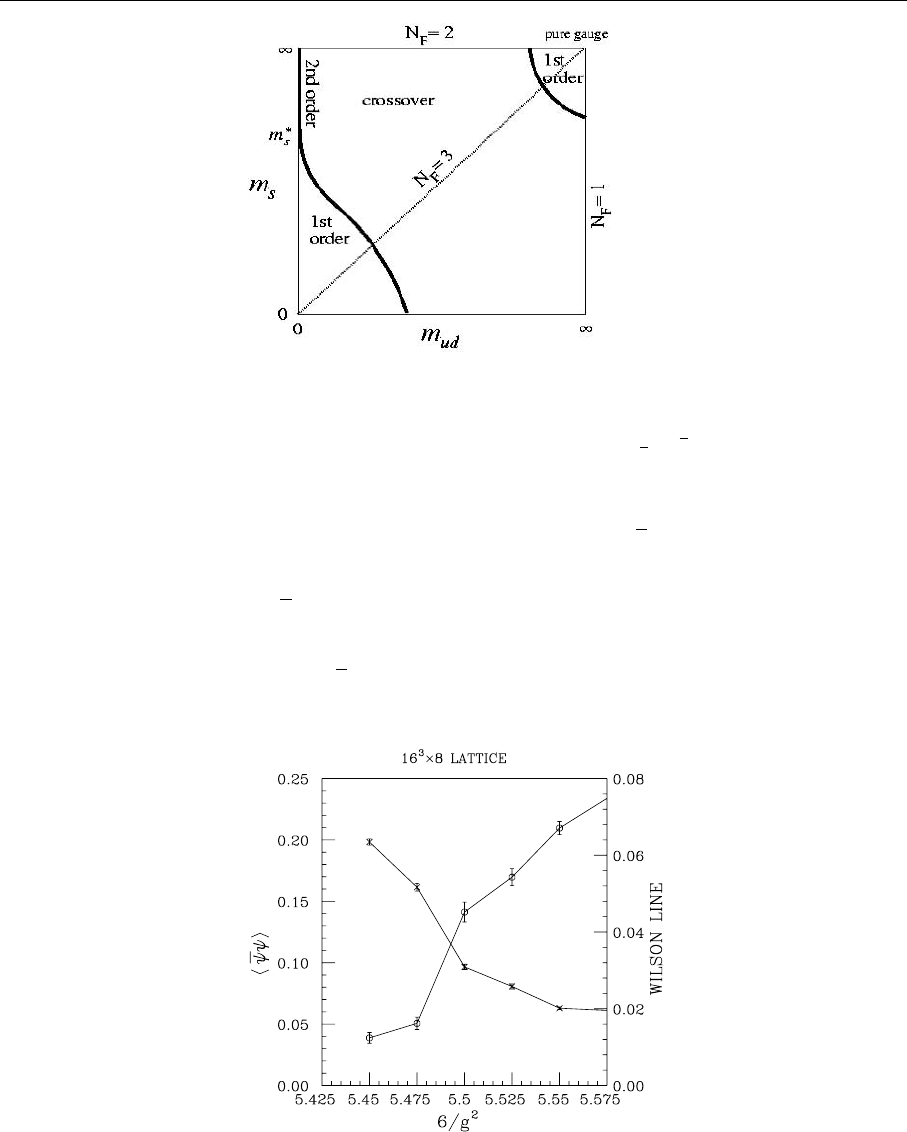
486 7. Nonperturbative QCD

Fig. 7.11. A still much de-

bated problem is the order

of the phase transition to

the plasma phase. The ﬁg-

ure shows a rough sketch

of the situation. For very

heavy or very light up,

down (m

, horizontal axis)

and strange (m

, vertical

axis) quarks the transition

is presumably ﬁrst-order.

The ﬁrst-order regions and

the smooth cross-over re-

gion are separated by a 2nd-

order phase transition line.

In the range of the physi-

cal masses the result could

be ﬁrst or second-order or

even a smooth transition be-

tween hadronic and quark

phase (from: K. Kanaya:

Nucl. Phys. Proc. Suppl. 47,

144 (1996))

Fig. 7.12. Lattice calcula-

tion of the Polyakov loop (or

Wilson line, which will be

explained in the following

section) and the chiral con-

densate as function of tem-

perature around the critical

temperature T

. The results

are taken from S. Gottlieb

et al. (MILC collabora-

tion): Phys. Rev. D 55, 6852

(1997)

) and right-handed (q

) quark states, which are obtained by acting with the

projectors on states with deﬁnite handedness q

−

)ψ. The condensate

measures the amount of coupling between left- and right-handed particles in the

vacuum. Therefore it is also called the “chiral” condensate. Beyond a critical

temperature its value vanishes, signaling the transition to a state with (nearly)

massless quarks and gluons. On the lattice, 

qq can be calculated as a path

integral of the trace of the propagator

qq=trG(x, x ) , (7.188)

using the master equation (7.23). Figure 7.12 shows the values of the Polyakov

loop and qq in a small temperature range around T

. One can observe the

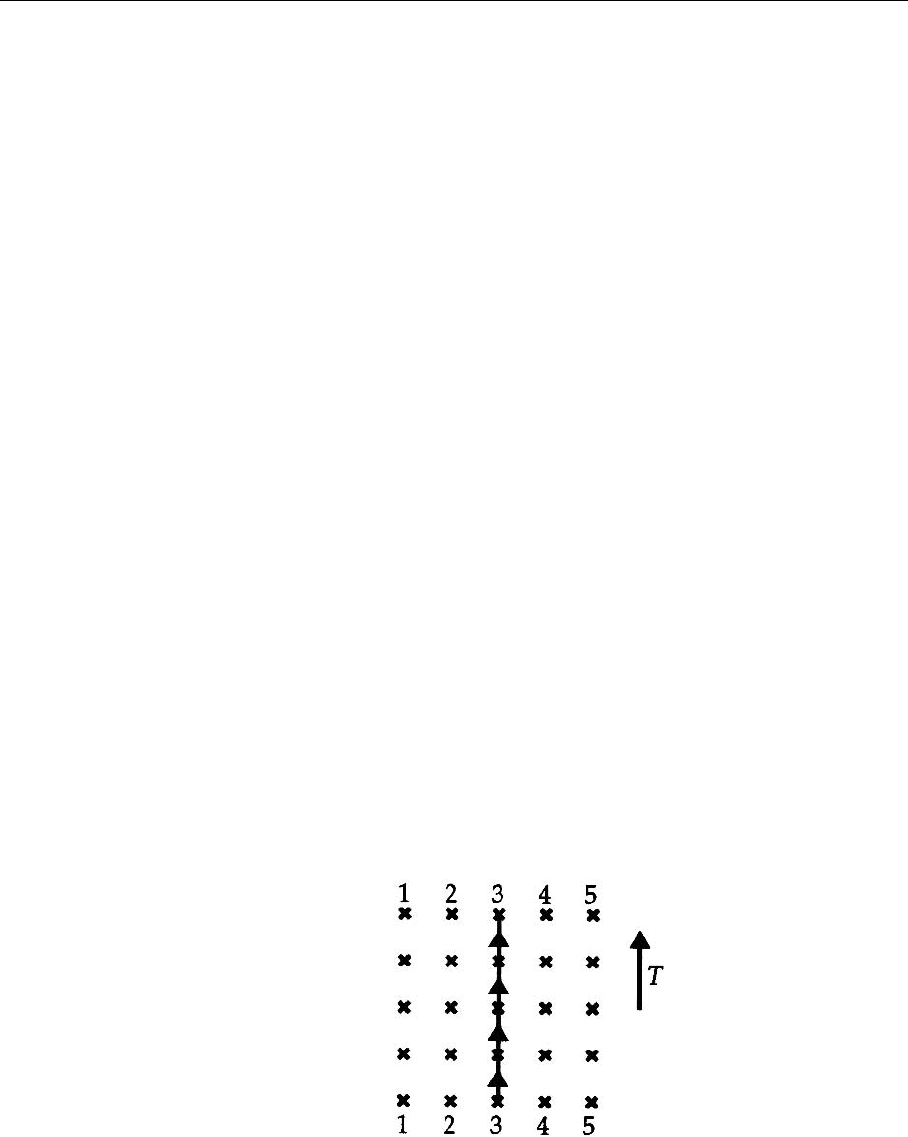
7.1 Lattice QCD Calculations 487

interesting behavior (also seen in many other calculations) that the critical tem-

peratures for the deconﬁnement phase transition and the chiral transition seem

to be identical. This is a nontrivial result as both phenomena relate to differ-

ent physical effects. The theoretical explanation of this behavior is still under

discussion.

7.1.18 The Polyakov Loop

In Sect. 7.1.15 on the string tension we have shown how to extract the static

potential between quarks from the expectation of Wilson loops. There is an

alternative method to do this. As mentioned, it is crucial to construct gauge-

invariant quantities (if we do not want to ﬁx the gauge on the lattice). Any

quantity with some unsaturated color indices like the untraced plaquette P

will exactly vanish if we average it over all gauge rotations P

=0. There is

a particularly useful type of gauge-invariant object we can specify on the lattice,

the so-called “Polyakov loop” (sometimes also called the “Wilson line”), given

by the following expression:

P(n) = tr

;

(n, n

). (7.189)

P(n) is deﬁned at every space point and is the product of timelike links in the time

direction (see Fig. 7.13). Since we have periodic boundary conditions in the time

direction it forms a “loop” on the lattice. The trace guarantees gauge invariance:

P(n) =tr G(n, 1)U

(n, 1)G

†

(n, 2)G(n, 2)U

(n, 2)G

†

(n, 3)...

G(n, N

(n, N

†

(n, Nτ +1)

=tr G(n, 1)

⎛

⎝

;

(n, nτ)

⎞

⎠

†

(n, N

+1)

= P(n) (7.190)

because of the periodicity G(n, 1) = G(n, N

+1).

Fig. 7.13. Graphical repre-

sentation of the Polyakov

loop. The links along the

time direction are multi-

plied, which yields a loop

structure because of the peri-

odic boundary conditions in

time

488 7. Nonperturbative QCD

The Polyakov loop has a rather simple physical meaning. If one considers an

inﬁnitely heavy quark sitting at a given point x in space and only propagating in

the time direction, the Euclidean Schrödinger equation, ϕ

(x,τ),isgivenby

∂

(x,τ)= i A

(x, τ)ϕ

(x,τ) . (7.191)

Thus we get a time-evolution operator S(τ) for the quark:

S(τ) = P exp

⎡

⎣

dτ



(x,τ



)

⎤

⎦

. (7.192)

Expression (7.192) is just the continuum version of the Polyakov loop. It de-

scribes the propagation of a static color charge on the lattice. Thus calculating

the expectation value of the Polyakov loop at ﬁnite temperature T , one calculates

the partition function of the system Z

including an open charge:

P(n)=Z

=exp

−F

(7.193)

with the free energy of the system F

. P serves as a signal for the deconﬁne-

ment phase transition. In the conﬁnement phase, color charges cannot propagate.

Therefore, adding a color charge to the system by hand generates an inﬁnite (or

very large, in the case of a ﬁnite-size lattice calculation) energy. Thus, according

to (7.193) the expectation value vanishes: P=0. However, beyond a critical

temperature one can observe a clear phase transition to ﬁnite values of P,sig-

nalling the possibility that open color charges can propagate. Figure 7.12 shows

the result of a lattice calculation. One can see that the Polyakov loop becomes

ﬁnite for temperatures T

∼250 MeV in a sharp transition that has been clearly

identiﬁed as a ﬁrst-order transition. This is the result if one neglects the fermionic

determinant as discussed in Sect. 7.1.7. If the effects of quarks are included,

the temperature drops to T

∼140 MeV. Here the order of the transition is still

subject to debate.

7.1.19 The Center Symmetry

There exists an interesting symmetry of lattice QCD in connection with the

Polyakov loop. Take the link variables in a hyperplane for some ﬁxed time, e.g.

= 1. One might transform all timelike links in this hyperplane by a unitary

3 ×3matrix

(n, n

=1) = CU

(n, n

= 1). (7.194)

Z belongs to the center of the gauge group, here SU(3). The center of a group is

deﬁned as the class of elements C which leave all group elements invariant under

transformation, i.e. which commute with all group elements: [C, U]=0.

7.1 Lattice QCD Calculations 489

It is clear that C has to be proportional to the unit matrix in order to fulﬁl this

requirement

C = e

iα11

with α ∈[0, 2π] . (7.195)

In addition, SU(N) requires the determinant of the group element to be 1.

Therefore we get

det C = 1 ⇒tr α

11 =0mod2π, (7.196)

which yields

2πn

, n = 0, 1, 2 . (7.197)

The three elements C

to C

form an own group, the Z(3). In general, the Z(N)

group (replace 3 by N in (7.197)) is the group of discrete rotations around the

unit circle in the complex plane.

In the limit N →∞we get continuous rotations, which is just the usual U(1)

of electrodynamics, for instance.

From the deﬁnition of the action for the gluons, (7.48), we see that under

a transformation (7.195) the action does not change. Factors C only enter in the

the part of the interaction containing space–time plaquettes. A plaquette in

the 41 plane, for example, is

(n, 1)U

(n, 2)U

†

(n +ae

, 1)U

†

(n, 1). (7.198)

Transforming the links by using (7.194), we get

=CU

†

. (7.199)

Since C commutes with all group elements one can shift C to the right and use

†

= 1. Thus P

Although the action is invariant under the center transformation, the

Polyakov loop is not, since it contains only one link belonging to the hyperplane

with n

=1. There we have the transformation property

P(n) =CP(n). (7.200)

As we have seen in the conﬁned phase, P=0 because an isolated color ﬁeld

is inﬁnitely heavy. In the deconﬁned phase one can have P = 0. This is also

a signal of spontaneous breaking of the center symmetry: the system clusters

around one of the three values of C

,i.e.P attains the corresponding phase

factor e

i2πn/3

. Otherwise, an averaging over the values of C

C=0 would

again generate a vanishing Polyakov loop. This intimate relation between the

Z(3) structure of the Polyakov loops and the conﬁnement/deconﬁnement phase

transition led to the idea that the critical behavior of the whole SU(3) theory can

be reduced to the one of a Z(3) spin model in three dimensions (as the Polyakov

loops P(n) are deﬁned in three dimensions).

The fact that both systems exhibit

a ﬁrst-order phase transition supports this idea.

See B. Svetitsky, L.G. Yaffe: Nucl. Phys. B 210, 423 (1982).