Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

500 7. Nonperturbative QCD
Exercise 7.3
=q
†
α
(0)q
δ
(0)
m
u
+m
d
2
γ
0
1
2
$
τ
b
,τ
a
%
αδ
+
m
u
−m
d
2
γ
0
τ
b
δ
a3
αδ
=
m
u
+m
d
2
¯
q(0) q(0)δ
ab
+
m
u
−m
d
2
¯
q(0)τ
b
q(0)δ
a3
. (10)
Finally we take the vacuum expectation value of this expression. As the vac-
uum cannot carry any quantum number, such as isospin, the second term does
not contribute:
d
3
x d
3
y
×
-
0
A
b
0
(0, x),
A
a
0
(0, O), m
u
¯
u(0, y)u(0, y) +m
d
¯
d(0, y)d(0, y)
0
.
=
m
u
+m
d
2
,
0
¯
u(0)u(0) +
¯
d(0)d(0)
0
δ
ab
. (11)
Let us now return to the QCD sum-rule calculation. We illustrate this method by
presenting all the detailed steps for one specific example: the calculation of the
mass. We wish to evaluate the left-hand side of (7.201) at the quark level, using
the condensates (7.202). The result will be compared with (7.206) and from this
comparison we shall extract an estimate for the mass.
The simplest contribution to (7.201) is just the perturbative graph. The flavor
structure of is simply
+
=
1
√
2
u
1
¯
d
2
−
¯
d
1
u
2
,
−
=−
1
√
2
d
1
¯
u
2
−
¯
u
1
d
2
,
0
=
1
2
d
1
¯
d
2
−u
1
¯
u
2
−
¯
d
1
d
2
−
¯
u
1
u
2
, (7.241)
implying that
,
j
µ
(x) j
ν
(0)
+
=−
1
2
,
u
1
(x)γ
µ
¯
d
2
(x)
d
1
γ
ν
¯
u
2
−
¯
u
1
γ
ν
d
2
(0)
·2
=
,
u
1
(x)γ
µ
¯
d
2
(x)
¯
u
1
(0)γ
ν
d
2
(0)
=
,
u(x)γ
µ
¯
d(x)
¯
u(0)γ
ν
d(0)
,
,
j
µ
(x) j
ν
(0)
0
=
,
¯
q(x)γ
µ
q(x)
¯
q(0)γ
ν
q(0)
. (7.242)
Thus we do not have to distinguish between up and down quarks, at least not
in the usual limit m
u
, m
d
→0. In the following we discuss the
0
case. For the
perturbative part (without any additive interactions or vacuum insertions) we get
Π
µν
(q) = i
d
4
x e
iqx
,
0
T
$
¯
q(x)γ
µ
q(x)
¯
q(0)γ
ν
q(0)
%
0
. (7.243)
7.2 QCD Sum Rules 501
Wick’s theorem simply gives
,
0
T {
¯
q(x)γ
µ
q(x)
¯
q(0)γ
ν
q(0)}
0
= (γ
µ
)
i
1
i
2
(γ
ν
)
i
3
i
4
,
0
T
$
¯
q
i
1
(x)q
i
2
(x)
¯
q
i
3
(0)q
i
4
(0)
%
0
= (γ
µ
)
i
1
i
2
(γ
ν
)
i
3
i
4
,
0
T
$
¯
q
i
1
(x)q
i
4
(0)
%
0
,
0
T
$
q
i
2
(x)
¯
q
i
3
(0)
%
0
= (γ
µ
)
i
1
i
2
(γ
ν
)
i
3
i
4
iS
F,i
4
,i
1
(−x) iS
F,i
2
,i
3
(x)
= tr
γ
µ
x/
2π
2
(x
2
)
2
γ
ν
−x/
2π
2
(x
2
)
2
=
1
π
4
x
2
g
µν
−2x
µ
x
ν
(x
2
)
4
. (7.244)
Using (1) from Exercise 4.6,
d
d
x
e
i p·x
(−x
2
)
ν
=−iπ
2
Γ(2 −ν +ε)
Γ(ν)
−4π
2
µ
2
p
2
ε
−p
2
4
ν−2
, (7.245)
it is easy to calculate the Fourier transformation of (7.244):
i
d
4
x e
i p·x
,
0
T {
¯
q(x)γ
µ
q(x)
¯
q(0)γ
ν
q(0)}
0
=i
d
4
x
E
e
−i p
E
·x
E
−1
π
4
x
2
E
g
µν
+2x
Eµ
x
Eν
x
2
E
4
=
−i
π
4
g
µν
+iπ
2
Γ(ε −1)
Γ(3)
−4π
2
µ
2
p
2
E
ε
p
2
E
4
−
i
π
4
2
−
∂
∂ p
Eµ
∂
∂ p
Eν
d
d
x
E
e
−i p
E
·x
E
1
x
2
E
4
=
1
8π
2
Γ(ε −1) p
2
E
−4π
2
µ
2
p
2
E
ε
g
µν
+
2i
π
4
(−iπ
2
)
Γ(ε −2)
Γ(4)
−4π
2
µ
2
ε
1
16
∂
∂ p
Eµ
∂
∂ p
Eν
p
2
E
2−ε
=
1
8π
2
Γ(ε −1) p
2
E
g
µν
−4π
2
µ
2
p
2
E
ε
+
1
8π
2
Γ(ε −2)
6
−4π
2
µ
2
p
2
E
ε
×
(2 −ε)(2 −ε)4 p
Eµ
p
Eν
+(2 −ε) 2 g
µν
p
2
E
=
1
8π
2
Γ(ε −1)
−4π
2
µ
2
p
2
E
ε
2
3
p
2
E
g
µν
+(1 −ε)
2
3
p
Eµ
p
Eν
=
1
8π
2
1
ε
+Γ
(1)
4π
2
µ
2
p
2
ε
2
3
p
2
g
µν
− p
µ
p
ν
+...
502 7. Nonperturbative QCD
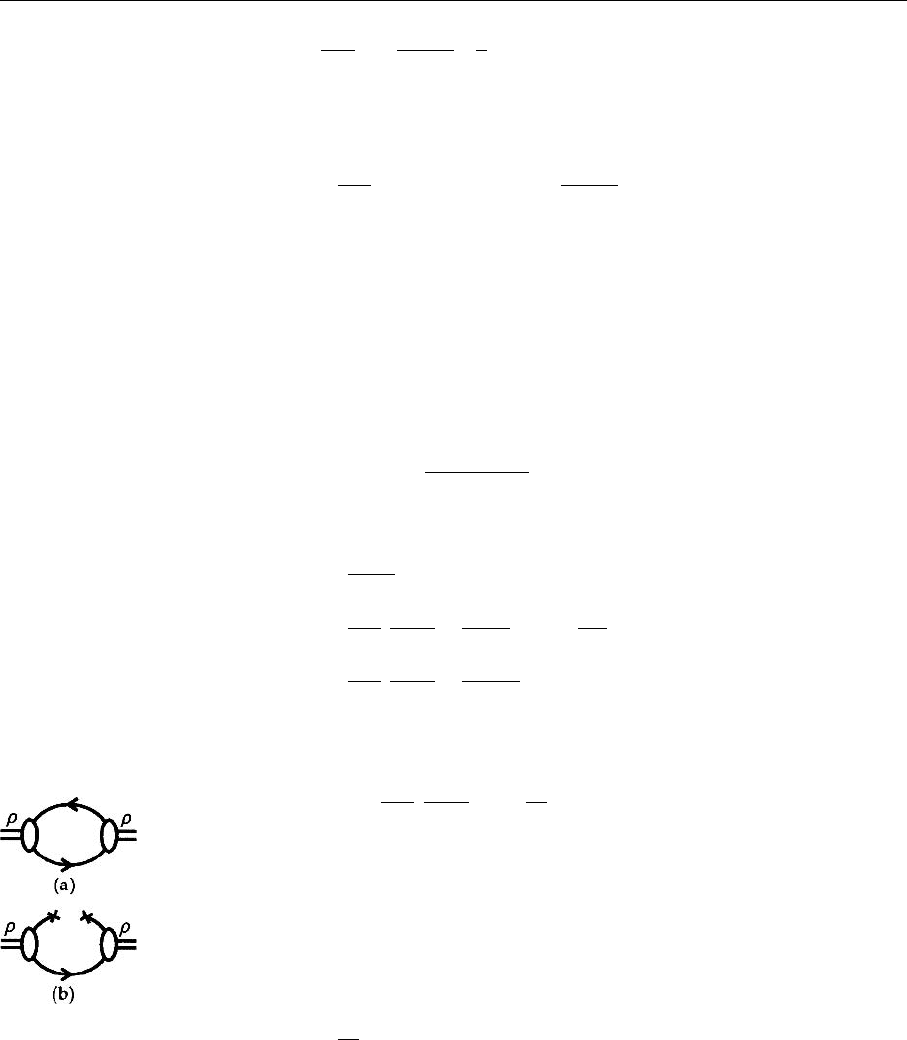
Fig. 7.16a,b. A graphical
representation of (a)the
lowest-order, purely pertur-
bative contribution, and (b)
the lowest quark condensate
contribution
=
1
8π
2
ln
4π
2
µ
2
p
2
2
3
p
2
g
µν
− p
µ
p
ν
+terms without an imaginary part . (7.246)
Every quark color gives the same contribution such that we get finally
Π
µν
=
1
4π
2
p
2
g
µν
− p
µ
p
ν
ln
4π
2
µ
2
p
2
+... . (7.247)
Thus we have calculated the perturbative contribution to lowest order of α
s
.
Clearly these perturbative contributions alone cannot be sufficient to completely
obtain nonperturbative quantities such as hadron masses. The fundamental as-
sumption of the QCD sum-rule approach is that these nonperturbative effects
can, to a good approximation, be described by vacuum properties. As the vac-
uum is supposed to be homogeneous, those fields coupling to it must have zero
momentum.
In the presence of background particles, the propagator of, for example,
a Dirac field is
S
F
(k) = (k/ +m)
1
k
2
−m
2
+iε
+2πi δ(k
2
−m
2
)Θ(k
0
) n(k)
. (7.248)
Assuming that n(k) = cmδ
3
(k), in coordinate space for m → 0 this becomes
S
F
(x) =
1
(2π)
4
d
4
k e
ik·x
S(k)
=
−i
2π
2
x/
(x
2
)
2
+
1
(2π)
3
d
4
k
cm
2m
δ
4
(k) e
ik·x
=
−i
2π
2
x/
(x
2
)
2
+
c
2(2π)
3
. (7.249)
Thus it would seem natural to describe the complex vacuum structure by adding
constant real numbers to the field propagators:
S
F
(x)
ab
ij
=
−i
2π
2
(x/)
ij
(x
2
)
2
δ
ab
−
1
12
,
¯
qq
δ
ab
δ
ij
. (7.250)
This form is also suggested by Wick’s theorem if the expectation values of
normal ordered products are interpreted as condensates.
T
ψ
a
i
(x)
¯
ψ
b
j
(x
)
=:ψ
a
i
(x)
¯
ψ
b
j
(x
) :+
,
0
T
ψ
a
i
(x)
¯
ψ
b
j
(x
)
0
, (7.251)
,
vac
T
$
ψ
a
i
(x)
¯
ψ
b
j
(x
)
%
vac
=
,
vac
: ψ
a
i
(x)
¯
ψ
b
j
(x
) :
vac
+
,
0
T
$
ψ
a
i
(x)
¯
ψ
b
j
(x
)
%
0
=−
1
12
δ
ab
δ
ij
¯
qq+iS
Fij
(x −x
)δ
ab
. (7.252)
Using (7.250) we shall next calculate the quark-condensate contribution to the
sum rule. It is represented by Fig. 7.16; Fig. 7.17 shows the lowest-order
perturbative contribution.

7.2 QCD Sum Rules 503
With (7.252) we simply get
Π
µν
=
a,b
i
d
4
x e
iqx
(γ
µ
)
i
1
i
2
(γ
ν
)
i
3
i
4
iS
Fi
4
i
1
(−x)
−
1
12
¯
qq
δ
ab
δ
i
2
i
3
=
−3i
12
¯
qq
d
4
x e
iqx
tr
γ
µ
γ
ν
S
F
(−x)
. (7.253)
For massless quarks the trace vanishes and we get strictly zero. Therefore we
expand S
F
in m and also keep the term linear in m:
−iS
F
(−x) =
1
(2π)
4
d
4
k e
ikx
k/ +m
k
2
−m
2
+iε
=
−i
2π
2
x/
(x
2
)
2
+
m
4π
2
1
x
2
+... . (7.254)
We thus get
Π
µν
=−
i
4
¯
qqm
d
4
x e
iqx
1
4π
2
4g
µν
1
x
2
=
π
2
4π
2
Γ(1)
Γ(1)
q
2
4
−1
−4π
2
µ
2
q
2
ε
m
¯
qqg
µν
=
1
q
2
m
¯
qqg
µν
=
1
q
2
+iη
m
¯
qqg
µν
. (7.255)
In the last step we have reintroduced the usual iη prescription, which we did not
write out explicitly during the calculation. As two graphs contribute, we have to
multiply this by a factor of 2. Also we know that Π
µν
is transverse, and we can
make this explicit by adding the q
µ
q
ν
term:
Π
µν
=
q
2
g
µν
−q
µ
q
ν
2
m
¯
qq
q
2
+iη
. (7.256)
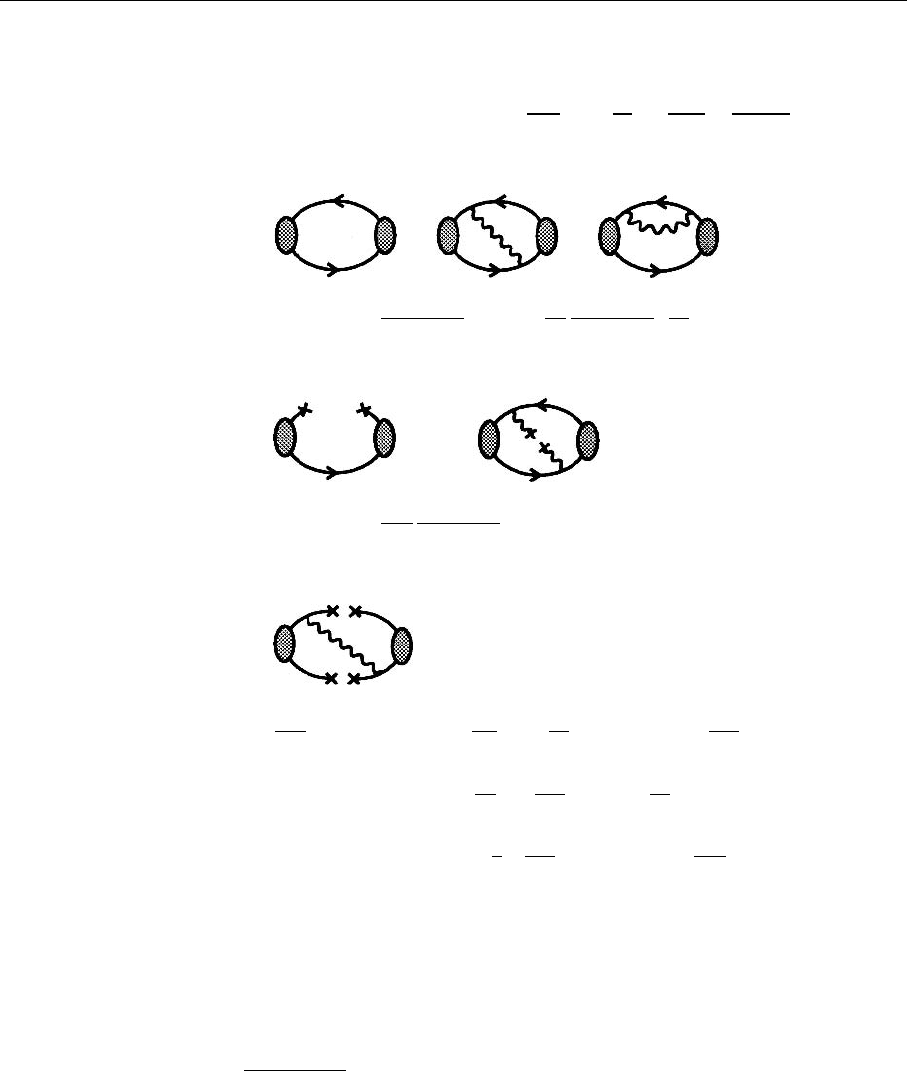
Next we calculate the lowest-order gluon condensate contributions, correspond-
ing to the graphs in Fig. 7.17.
The fields coupling to condensates all have zero momentum, since the vac-
uum condensates are time and space independent. Thus the gluon field can be
easily expressed in terms of the constant gluon field strengths G
a
µν
,
A
a
µ
(z) =
1
2
z
G
a
µ
(0) (7.257)
⇒ ∂
ν
A
a
µ
(z) −∂
µ
A
a
ν
(z) +gf
abc
A
b
µ
(z)A
c
ν
(z)
=
1
2
G
a
νµ
(0) −
1
2
G
a
µν
(0) +g
1
4
z
α
z
β
f
abc
G
b
αµ
(0) G
c
βν
(0)
= G
a
νµ
(0), (7.258)
Fig. 7.17. Lowest-order
couplings to the gluon con-
densate
504 7. Nonperturbative QCD
where we have used the fact that G
a
νµ
(0) is the same for all colors, since the
vacuum does not distinguish any color state G
b
αµ
(0) = G
c
βν
(0).
The quark propagator in coordinate space in the gluon background fields of
the vacuum condensates is then
−iS(x, y; A) =
1
2π
2
(x −y) ·γ
(x −y)
4
−
gG
µ
(0)
4π
4
×
1
2
d
4
z
x/ −z/
(x −z)
4
z
γ
µ
z/ −y/
(z −y)
4
+
g
2
G
µ
(0)G
µ
(0)
8π
6
×
1
4
d
4
z
1
d
4
z
2
x/ −z/
1
(x −z
1
)
4
(z
1
)
γ
µ
z/
1
−z/
2
(z
1
−z
2
)
4
×(z
2
)
γ
µ
z/
2
−y/
(z
2
−y)
4
+... . (7.259)
We have to perform these integrals using dimensional regularization. In Exer-
cise 7.4 we do this for the first integral on the right-hand side. The double integral
and all higher ones vanish. The result is then
S(x, y; A) =i
1
2π
2
r/
(r
2
)
2
+
ig
32π
2
r
2
r/γ
µ
γ
−γ
γ
µ
r/
G
µ
(0)
+
ig
4π
2
r
4
r/y
x
µ
G
µ
(0)
(7.260)
with
r
µ
= x
µ
−y
µ
. (7.261)
EXERCISE
7.4 Calculation of QCD Sum-Rule Graphs
with Dimensional Regularization
Problem. Calculate the first integral in (7.259) using the techniques of dimen-
sional regularization introduced in Sect. 4.3.
Solution. We first introduce the usual Feynman parameters:
I =
d
4
z
(x/ −z/)γ
µ
(z/ −y/)z
(x −z)
4
(z −y)
4
= Γ(4)
duu(1 −u)
d
4
z
(x/ −z/)γ
µ
(z/ −y/)z
u(x −z)
2
+(1 −u)(z −y)
2
4
. (1)
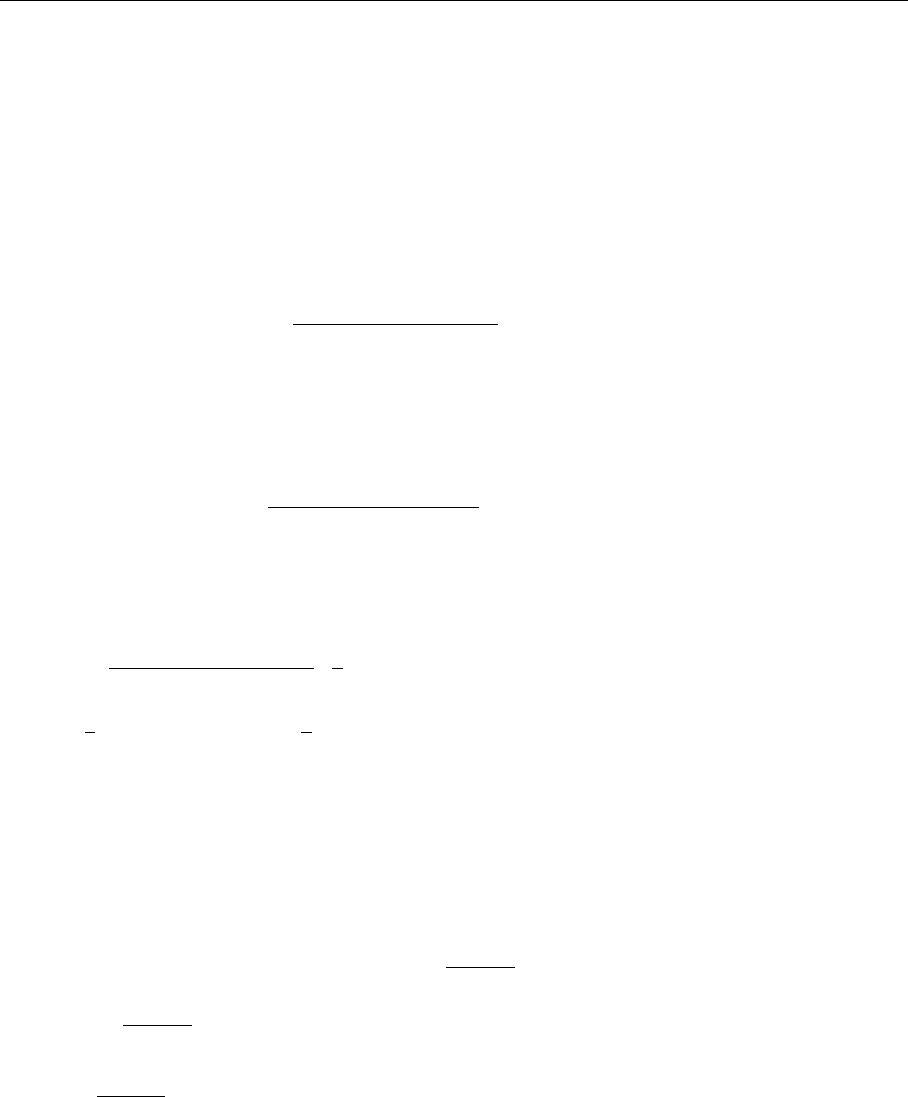
7.2 QCD Sum Rules 505
Then, as usual, we bring the denominator into the quadratic normal form:
u(x −z)
2
+(1 −u)(z −y)
2
= z
2
−2z
ux +(1 −u)y
+ux
2
+(1 −u)y
2
=
z −
ux +(1 −u)y
2
+u(1 −u)x
2
+u(1 −u)y
2
−2u(1 −u)x · y
=
z −
ux +(1 −u)y
2
+u(1 −u)(x −y)
2
. (2)
Substituting z → z +ux +(1 −u)y gives
I = Γ(4)
duu(1 −u)
d
4
z
(1 −u)(x/ −y/) −z/
γ
µ
z
2
+u(1 −u)(x −y)
2
4
×
z/ +u(x/ −y/)
z
+ux
+(1 −u)y
. (3)
Only the terms even in z contribute to the integral, and z
z
α
contribute z
2
g
α
/4:
I = 6
1
0
duu(1 −u)
d
4
z
(1 −u)u(x/ −y/)γ
µ
(x/ −y/)
z
2
+u(1 −u)(x −y)
2
4
×
ux
+(1 −u)y
+6
1
0
duu(1 −u)
×
d
4
z
z
2
+u(1 −u)(x −y)
2
4
#
1
2
z
2
γ
µ
ux
+(1 −u)y
+
1
4
z
2
(1 −u)(x/ −y/)γ
µ
γ
−
1
4
z
2
γ
γ
µ
u(x/ −y/)
&
. (4)
The nominator of the second integral is abbreviated by writing z
2
· f(u).Wenow
integrate using (4.97) and (4.99):
I = 6
1
0
duu(1 −u)
#
u(1−u)(x −y)
2
−2
×u(1 −u)(x/ −y/)γ
µ
(x/ −y/)
ux
+(1 −u)y
iπ
2
Γ(2)
Γ(4)
+ f(u)
iπ
2
Γ(1)
Γ(4)
2
u(1−u)(x −y)
2
−1
&
=iπ
2
1
(x −y)
4
1
0
du (x/ −y/)γ
µ
(x/ −y/)
ux
+(1 −u)y
Exercise 7.4
506 7. Nonperturbative QCD
Exercise 7.4
+2
1
0
du
1
2
γ
µ
ux
+(1 −u)y
+
1
4
(1 −u)(x/ −y/)γ
µ
γ
−
1
4
γ
γ
µ
u(x/ −y/)
(x −y)
2
. (5)
Both the integral
+
u du and
+
(1 −u) du give 1/2
I =
iπ
2
2
1
(x −y)
4
(x/ −y/)γ
µ
(x/ −y/)(x +y)
+γ
µ
(x
+y
)(x −y)
2
+
1
2
(x/ −y/)γ
µ
γ
−γ
γ
µ
(x/ −y/)
(x −y)
2
=
iπ
2
4
1
(x −y)
2
(x/ −y/)γ
µ
γ
−γ
γ
µ
(x/ −y/)
+
iπ
2
2
1
(x −y)
4
2(x −y)
µ
(x/ −y/)(x +y)
=
iπ
2
4
1
(x −y)
2
(x/ −y/)γ
µ
γ
−γ
γ
µ
(x/ −y/)
+iπ
2
1
(x −y)
4
x
µ
x
+x
µ
y
−y
µ
x
−y
µ
y
(x/ −y/) . (6)
This still has to be multiplied by G
µ
(0), which is antisymmetric in and µ,
leading to
∆S(x, y ; A) =−
ig
32π
2
1
(x −y)
2
(x/ −y/)γ
µ
γ
−γ
γ
µ
(x/ −y/)
G
µ
(0)
−
ig
8π
2
1
(x −y)
2
2x
µ
y
(x/ −y/)G
µ
(0). (7)
Only the first graphs in Fig. 7.17 have to be calculated:
0|T {
¯
q(x)γ
µ
q(x)
¯
q(0)γ
ν
q(0)}|0
⇒(γ
µ
)
i
1
i
2
(γ
ν
)
i
3
i
4
i
−
i
32π
2
[x/γ
µ
γ
−γ
γ
µ
x/]
i
4
i
1
G
µ
(0)
(x −y)
2
×i
+
i
32π
2
[x/γ
µ
γ
−γ
γ
µ
x/]
i
2
i
3
G
µ
(0)
(x −y)
2
=−G
µ
(0)G
µ
(0)
g
2
32 ·32π
4
1
(x −y)
4
×tr{[x/γ
µ
γ
−γ
γ
µ
x/]γ
µ
[x/γ
µ
γ
−γ
γ
µ
x/]γ
ν
}=:T
µν
. (7.262)

7.2 QCD Sum Rules 507
Now we also have to insert the SU(3) matrices to express G
µ
G
µ
by the
vacuum condensate:
α
s
π
G
µ
G
µ
→tr
#
λ
a
2
λ
b
2
&
α
s
π
G
a
µ
G
b
µ
=
1
2
α
s
π
G
a
µ
G
b
µ
=const ·
-
0
α
s
π
G
a
αβ
G
aαβ
0
.
g
g
µ
µ
−g
µ
g
µ
. (7.263)
To determine the constant we contract with g
g
µ
µ
:
1
2
α
s
π
G
a
µ
G
a
µ
= const ·
-
0
α
s
π
G
a
αβ
G
aαβ
0
.
(16 −4)
⇒const =
1
24
. (7.264)
Inserting this into (7.262) yields
−
-
0
α
π
G
a
αβ
G
aαβ
0
.
1
32 ·8π
2
·
1
24
·
1
x
2
7
×
tr
x/γ
µ
γ
−γ
γ
µ
x/
γ
µ
x/γ
µ
γ
−γ
γ
µ
x/
γ
ν
−tr
x/γ
γ
µ
−γ
µ
γ
x/
γ
µ
x/γ
µ
γ
−γ
γ
µ
x/
γ
ν
. (7.265)
The traces give
tr
$
−2x/γ
µ
γ
µ
x/γ
µ
γ
ν
+2x/γ
µ
γ
µ
γ
µ
x/γ
ν
+2γ
µ
x/γ
µ
x/γ
µ
γ
ν
−2γ
µ
x/γ
µ
γ
µ
x/γ
ν
−4x
ν
γ
µ
γ
µ
x/γ
µ
+4g
µ
ν
x/γ
µ
x/γ
µ
+4g
µµ
γ
µ
x/γ
ν
x/ −4x
µ
γ
µ
γ
µ
x/γ
ν
%
=tr
$
−8x
2
γ
µ
γ
ν
−8x/γ
µ
x/γ
ν
−8γ
µ
γ
ν
x
2
−16x
ν
x
µ
+8γ
µ
x/γ
ν
x/ −16x
µ
x/γ
ν
%
=−16x
2
·4g
µν
−32 ·4x
ν
x
µ
=−64
x
2
g
µν
+2x
µ
x
ν
,
T
µν
=
1
96π
2
-
0
α
π
G
a
αβ
G
aαβ
0
.
x
2
g
µν
+2x
µ
x
ν
x
2
2
. (7.266)
This leads to the same integral we encountered in (7.255) repeating the same
calculations therefore gives
Π
µν
=
1
96π
2
-
0
α
π
G
a
αβ
G
aαβ
0
.
4π
2
q
2
2
q
2
g
µν
−q
µ
q
ν
·2
=
1
2
(q
2
g
µν
−q
µ
q
ν
)
1
(q
2
+iε)
2
-
α
s
π
G
a
αβ
G
aαβ
.
. (7.267)
508 7. Nonperturbative QCD
It should now be obvious how to proceed further. Taking into account the
following graphs we get
17
Π
µν
(q) = (q
2
g
µν
−q
µ
q
ν
)
#
−
1
4π
2
1 +
α
s
π
ln
−q
2
µ
2
−
6m
2
q
2
+iε
+
2
(q
2
+iε)
2
m
¯
qq+
1
12
1
(q
2
+iε)
2
-
α
s
π
G
a
αβ
G
aαβ
.
+
112
91
πα
s
(q
2
+iε)
3
¯
qq
2
&
. (7.268)
1
3q
2
Im Π
µν
(q)g
µν
=
)
1
4π
1 +
α
s
π
−m
¯
qqπ
−
∂
∂q
2
δ
q
2
−
π
12
−
∂
∂q
2
δ
q
2
-
α
s
π
G
a
αβ
G
aαβ
.
−
'
1
2
∂
∂q
2
2
δ
q
2
(
2π ·
112
91
¯
qq
2
πα
s
*
.
(7.269)
We have so far calculated the partonic Π
µν
(q
2
) tensor. Next we have to relate our
result to the hadron description of Π
µν
(q
2
). The quark description used a current
with the quantum numbers of the rho. However, several resonances exist with
such quantum numbers as well as continuum states. The unique property of the
rho is that it is the lightest state and this property can be used to project it out
17
L.J. Reinders, H. Rubinstein and S. Yazaki: Phys. Rep. 127, 1 (1985).
V.A. Novikov, M.A. Shifman, A.I. Vainshtein and V.I. Zakharov: Fortsch. Phys. 32,
585 (1985).
7.2 QCD Sum Rules 509
from both the hadron and the parton descriptions. There are various methods to
do this; we wish to discuss here only one, the Borel transformation, defined by
I =
1
πM
2
∞
0
e
−s/M
2
Im [Π(s)] ds . (7.270)
Inserting (7.206) into this expression and replacing the upper integration bound
by s
0
gives
I =
1
πM
2
s
0
0
e
−s/M
2
Im (Π(s)) ds
=
1
πM
2
f
3π
e
2
f
R
m
2
R
g
2
R
e
−m
2
R
/M
2
. (7.271)
Obviously for small enough M
2
only the lowest-mass state survives. Here, how-
ever, we run into problems, since M
2
cannot be arbitrarily small, or otherwise
the highest-twist contributions to the partonic description would become arbi-
trarily large. To understand this one has to know that the Borel transformation is
equivalent to the following mathematical operation:
1
πM
2
s
0
0
e
−s/M
2
Im [Π(s)] ds
= lim
Q
2
,n→∞, Q
2
/n=M
2
=const
1
(n −1)!
Q
2n
−
d
dQ
2
n
Π(Q
2
)
= lim
Q
2
,n→∞, Q
2
/n=M
2
nQ
2n
π
s
0
0
Im Π(s)
s +Q
2
n+1
ds
= lim
Q
2
,n→∞, Q
2
/n=M
2
n
πQ
2
s
0
0
Im Π(s)
1 +
s
Q
2
n+1
ds
= lim
Q
2
,n→∞, Q
2
/n=M
2
1
πM
2
s
0
0
e
−(n+1) ln(1+s/Q
2
)
Im Π(s) ds
=
1
πM
2
s
0
0
e
−s/M
2
Im Π(s) ds , (7.272)
where we have started from the well-known dispersion relation
Π
q
2
=
1
π
s
0
0
Im Π(s)
s +Q
2
ds . (7.273)
