Greiner W., Schrammm S., Stein E. Quantum Chromodynamics
Подождите немного. Документ загружается.

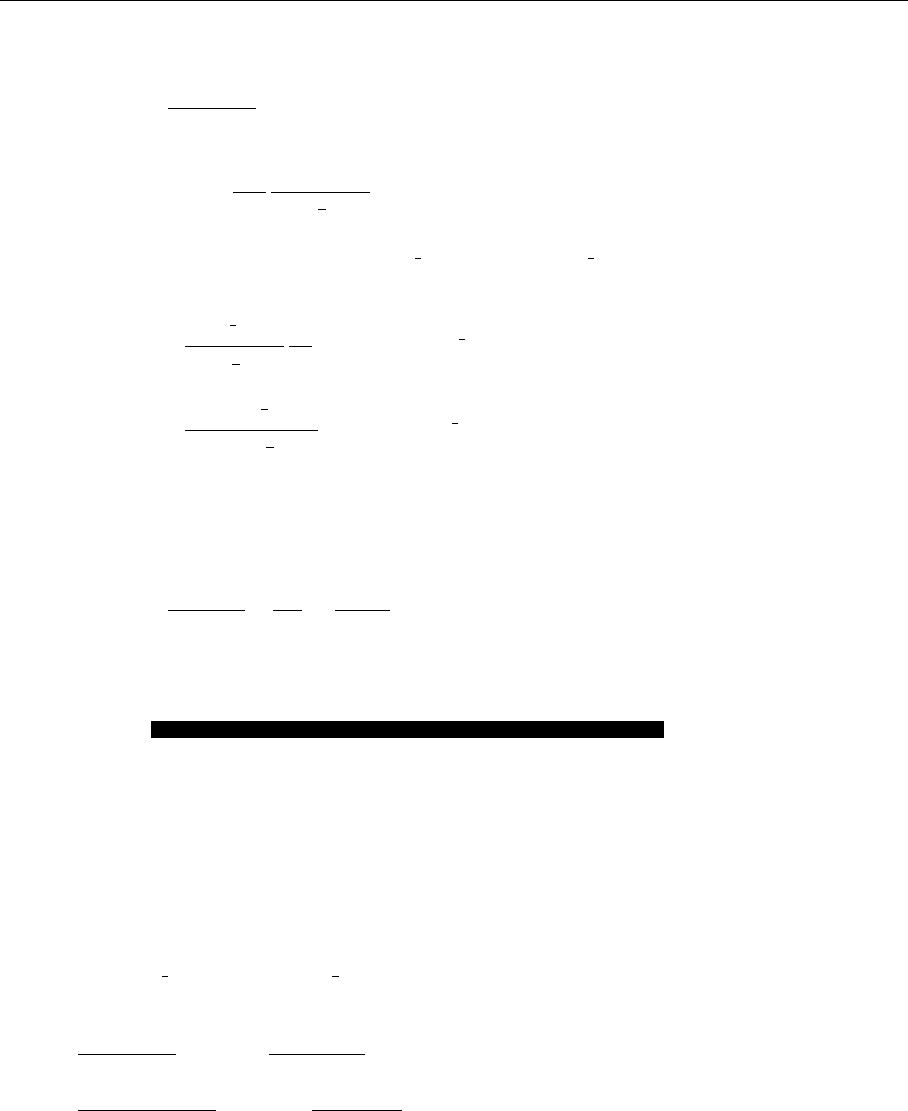
8.1 The Ground State of QCD 521
and use
(ω
2
−iδ)
ν−µ
=
i
−ν+η
Γ(−ν +η)
∞
0
dττ
−ν+η−1
e
−iτ(ω
2
−iδ)
(8.29)
ε −ε(H = 0) = lim
η,δ→0
⎡
⎣
gH
2π
2
i
−1/2+η
Γ
−
1
2
+η
∞
0
dk
∞
0
dττ
−3/2+η
×e
−iτ(k
2
−iδ)
)
∞
n=1
e
−iτ2gH
n−
1
2
+
∞
n=0
e
−iτ2gH
n+
3
2
*
−
i
−
1
2
+η
Γ
−
1
2
+η
1
π
2
∞
0
dk
∞
0
dτk
2
τ
−
3
2
+η
e
−iτ(k
2
−iδ)
+
gHi
−
1
2
+η
2π
2
Γ
−
1
2
+η
∞
0
dk
∞
0
dττ
−
3
2
+η
e
−iτ(k
2
−iδ−gH )
⎤
⎦
.
(8.30)
The calculation of the integrals is demonstrated in Exercise 8.1. The result is
ε −ε(H = 0) =
11(gH )
2
48π
2
ln
gH
µ
2
−i
(gH )
2
8π
. (8.31)
EXERCISE
8.1 The QCD Vacuum Energy Density
Problem. Derive (8.31) from (8.30).
Solution. The sums in (8.30) can be directly evaluated:
∞
n=1
e
−iτ2gH
n−
1
2
+
∞
n=0
e
−iτ2gH
n+
3
2
=
e
iτgH
1 −e
−iτ2gH
−e
iτgH
+
e
−3iτgH
1 −e
−2iτgH
=
e
2iτgH
+e
−2iτgH
e
iτgH
−e
−iτgH
−e
iτgH
=
cos(2gHτ)
isin(gHτ)
−e
iτgH
. (1)
522 8. Phenomenological Models for Nonperturbative QCD Problems
Exercise 8.1
Also the k integrations can be directly performed:
∞
0
dk e
−iτk
2
=
1
2
!
π
τ
e
−i
π
4
,
∞
0
dkk
2
e
−iτk
2
= i
∂
∂τ
∞
0
dk e
−iτk
2
=−
i
4
√
π
τ
3
2
e
−i
π
4
. (2)
Therefore we get
ε −ε(H = 0)
= lim
η,δ→0
⎡
⎣
gH
4π
3
2
e
−i
π
2
+i
π
2
η
Γ
−
1
2
+η
∞
0
dττ
−2+η
e
−δτ
cos(2gHτ)
isin(gHτ)
−e
iτgH
+
i
4
e
−i
π
2
+i
π
2
η
π
3
2
Γ
−
1
2
+η
∞
0
dττ
−3+η
e
−δτ
+
gH
4
e
−i
π
2
+i
π
2
η
π
3
2
Γ
−
1
2
+η
∞
0
dττ
−2+η
e
iτgH−δτ
⎤
⎦
. (3)
Now we employ the relation
cos(2gHτ) = 1 −2sin
2
(gHτ) , (4)
which yields
cos(2gHτ)
isin(gHτ)
−e
iτgH
=
1
isin(gHτ)
−
2
i
1
2i
e
iτgH
−e
−iτgH
−e
iτgH
=
1
isin(gHτ)
−e
−iτgH
→
1
isin(gHτ −i
˜
η)
−e
−iτgH
. (5)
Here we have defined the singularities by inserting i
˜
η(
˜
η>0). The integral ex-
ists provided η>2. We calculate it in this region and determine its value for
η → 0 by analytic continuation. This very procedure has already been used in
dimensional regularization. Identity (5) ensures that the integrand vanishes for
τ = R e
iφ
, −
π
2
<φ<0,R →∞. Therefore the integral surrounding the fourth
quadrant vanishes:
dτ ···=
∞
0
dτ ···+
0
−i∞
dτ ···=0 , (6)

8.1 The Ground State of QCD 523
Since the integrand has no singularities, we substitute τ =−is and evaluate the
last integral with the help of (8.29):
ε −ε(H = 0)
= lim
η,δ→0
⎡
⎣
gH
4π
3
2
−ie
i
π
2
η
Γ
−
1
2
+η
(−i)
−1+η
×
∞
0
dss
−2+η
e
−δr
1
sinh(gHs)
−e
−sg H
+
e
i
π
2
η
(−i)
−2+η
4π
3
2
Γ
−
1
2
+η
∞
0
dss
−3+η
gH
4
e
−i
π
2
+i
π
2
η
π
3
2
Γ
−
1
2
+η
×
(−1+η)
e
i
π
2
(−1+η)
(−gH +iδ)
1−η
⎤
⎦
. (7)
Finally we substitute s = v/gH:
ε −ε(H = 0) = lim
η→0
(gH )
2−η
4π
3
2
1
Γ
−
1
2
+η
×
⎡
⎣
∞
0
dvv
−2+η
1
sinh(v)
− e
−v
−
1
v
−(−1 +η)(−)
n
⎤
⎦
. (8)
The integral of e
−v
leads to a gamma function:
∞
0
dvv
−2+η
e
−v
= Γ(−1 +η) , (9)
while the integral over 1/ sinh v −1/v can be split into a finite part and one that
diverges in the limit η → 0:
∞
0
dvv
−2+η
1
sinh(v)
−
1
v
=
∞
0
dvv
−2+η
1
sinh(v)
−
1
v
+
1
6
v
−
1
6
∞
0
dvv
−1+η
=C −
1
6
1
η
, (10)
Exercise 8.1

524 8. Phenomenological Models for Nonperturbative QCD Problems
Exercise 8.1
ε −ε(H = 0) = lim
η→0
(gH )
2−η
4π
3
2
Γ
−
1
2
+η
×
#
C −
1
6
1
η
−Γ
(
−1+η
)
1 +(−)
η
&
. (11)
With
Γ(−1 +η) =
1
−1+η
Γ(η) =
Γ(1 +η)
(−1+η)η
(12)
we are now able to calculate the limiting case η → 0:
(gH )
2−η
=(gH)
2
(1 −η ln(gH) +···),
Γ
−
1
2
+η
=Γ
−
1
2
1 +ηΨ
−
1
2
+···
=−2
√
π
1 +ηΨ
−
1
2
+··· , (13)
Γ(−1 +η) =
−1−η
η
[1 +ηΨ(1)]+··· ,
(−)
η
=1 +ηiπ,
⇒ε −ε(H = 0) = lim
η→0
#
(gH )
2
8π
2
η
+
(gH )
2
8π
2
11
6
ln(gH) +C
−iπ
&
.
(14)
Here all constants have been absorbed into C
, which does not depend on H.
The divergent first part can be renormalized. The renormalized, i.e., the physical,
energy density is then
ε −ε(H = 0) =
11
6
(gH )
2
8π
2
ln(gH ) +C
−i
(gH )
2
8π
. (15)
In the transition to (8.28), however, we should have introduced a factor m
2η
in
order to conserve the dimension (m is supposed to be an energy). Then we obtain
11(gH )
2
48π
2
ln
gH
m
2
+
6
π
C
=
11(gH )
2
48π
2
ln
gH
µ
2
, (16)
where C
has been absorbed by the definition of µ
µ
2
=m
2
e
−6C
/11
, (17)
ε −ε(H = 0) =
11(gH )
2
48π
2
ln
gH
µ
2
−i
(gH )
2
8π
. (18)
It should be noticed that the techniques used in this exercise to calculate (8.31)
are practically the same as those introduced systematically in Sect. 4.3 in the
context of dimensional regularization.

8.1 The Ground State of QCD 525
The presence of the imaginary part is again an indication of the instability. If we
minimize the real part of the vacuum energy H
2
/2 (see the last term in (8.9)),
we obtain a minimum at H =0:
∂
∂H
1
2
H
2
+
11(gH )
2
48π
2
ln
gH
µ
2
= H +
11g
2
H
24π
2
ln
gH
µ
2
+
1
2
=0
⇒ gH = µ
2
exp
−
24π
2
11g
2
+
1
2
, (8.32)
which does not fix the value of gH since µ
2
wasarbitraryuptonow.Aswe
have effectively performed a dimensional regularization, µ
2
is proportional to
the renormalization scale. Indeed, the real part of ε −ε(H = 0) can be deduced
from renormalization group properties in a very elegant fashion. The prefactor
then comes from the β function:
1
2g
β ←→
g
2
32π
2
11 ×2
3
=
11g
2
48π
2
for SU(2). (8.33)
We demonstrate this in Example 8.2 to show the strength of renormalization
group arguments. However, this example will also show the weakness of these
techniques, since one tacitly uses a number of assumptions without being able to
check their validity. So the renormalization group treatment gives no indication
of the existence of unstable states and predicts a constant color magnetic field;
but the presence of unstable modes shows that this is not a physical solution.
In order to have any hope of obtaining a realistic ground state a consistent
treatment of the unstable modes has to be developed. We shall not perform
these calculations explicitly but only illustrate the ideas. There is a well-known
method of treating unstable modes from the problem of spontaneous symmetry
breaking. Here, too, the usual vacuum modes are not stable, and the field drifts
into a finite vacuum expectation value. If the Higgs field is expanded instead
around this vacuum expectation value, only stable modes are seen. By analogy
to this, one is led to the following procedure for treating unstable modes.
1. Isolate the unstable modes and rewrite the Lagrange density to have them
appear in the same way as Higgs fields.
2. Insert nonvanishing vacuum expectation values and determine the energeti-
cally optimal gauge field configuration.
The first step can indeed be performed. The second step is very difficult and
only possible in the framework of certain ansätze. We therefore show just one
of the results (see Fig. 8.3).
1
Other ansätze yield slightly different results but
a domain structure at a length scale
√
gH
0
in the xy plane is always found, and
compensating positive and negative fields in H in large spatial regions. One can
immediately imagine why no unstable modes appear in these solutions.
1
See J. Ambjørn and P. Olesen: Nucl. Phys. B 170, 60 (1980).
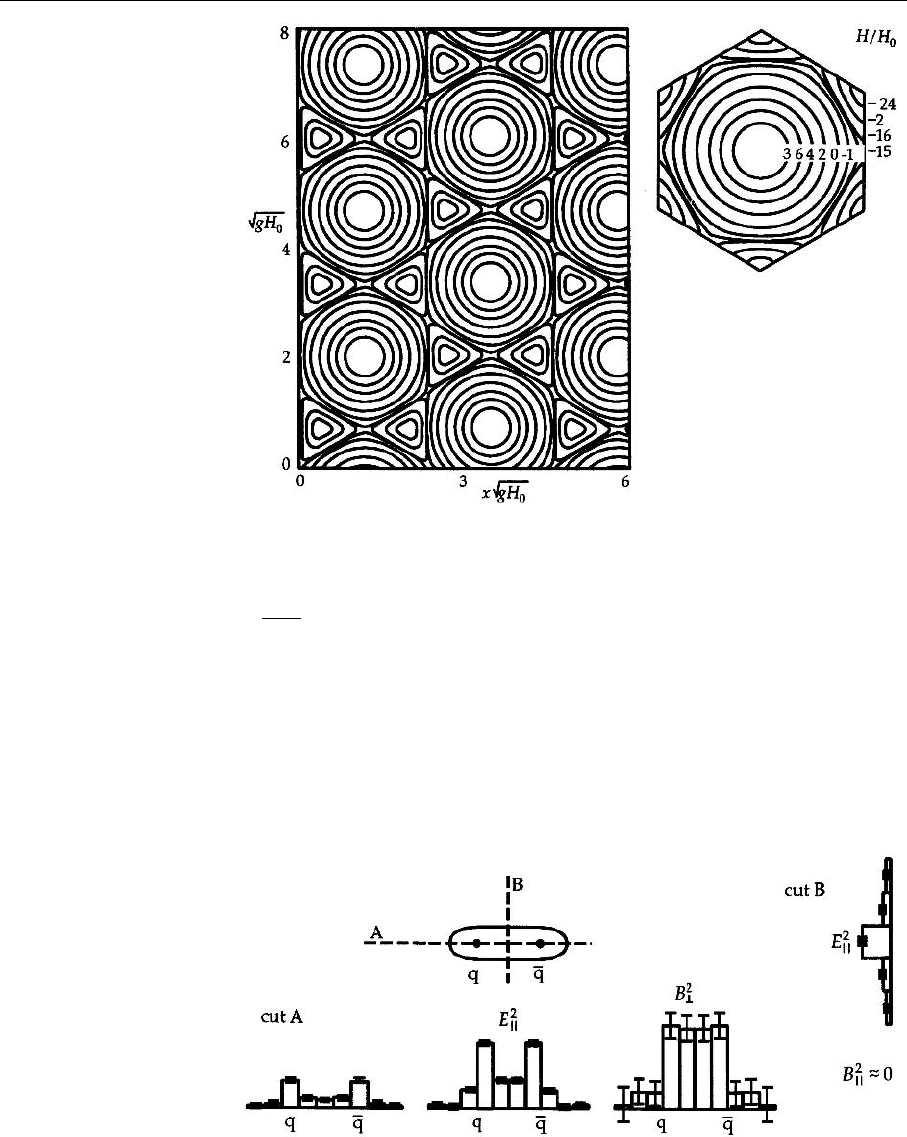
526 8. Phenomenological Models for Nonperturbative QCD Problems
Fig. 8.3. The Ambjørn–Ole-
sen solution for the QCD
ground state. The H field
is parallel to the z axis.
Contour lines are at 0.8H
0
,
0.6H
0
,0.4H
0
,0.2H
0
,0.0H
0
,
−0.1H
0
, −0.15H
0
, −0.16H
0
,
−0.2H
0
, −0.24H
0
(J. Amb-
jørn and P. Olesen: Nucl.
Phys. B 170, 60 (1980))
Fig. 8.4. The result of
a Monte Carlo calcula-
tion for color electric and
color magnetic fields around
a static quark–antiquark
pair. || denotes the direc-
tion parallel to the A axis.
(From J.W. Flower and S.W.
Otto: Phys. Lett. B 160,
128 (1985).) The color mag-
netic fields are enlarged
by a factor of 10
The lowest Landau state (n = 0) extends over large spatial domains. There-
fore the H fields average out and the term ±2gH≈0 no longer leads to
instabilities. The higher Landau states are localized in the xy plane up to
√
gM
0
/n and thus experience a more or less constant H field,which,ashasjust
been calculated, leads to a lowering of the energy. Figure 8.3 shows a system of
parallel tubes made of color magnetic fields that are completely analogous to vor-
tices in type II superconductors. This parallel supports the picture of the QCD
vacuum as a dual superconductor. Figure 8.3 has been calculated as a solution of
the classical field equations. In quantum mechanics, fields will oscillate around
this configuration. In particular, the magnetic flux tubes will no longer be strictly
parallel but change their orientation over large spatial regions. This property
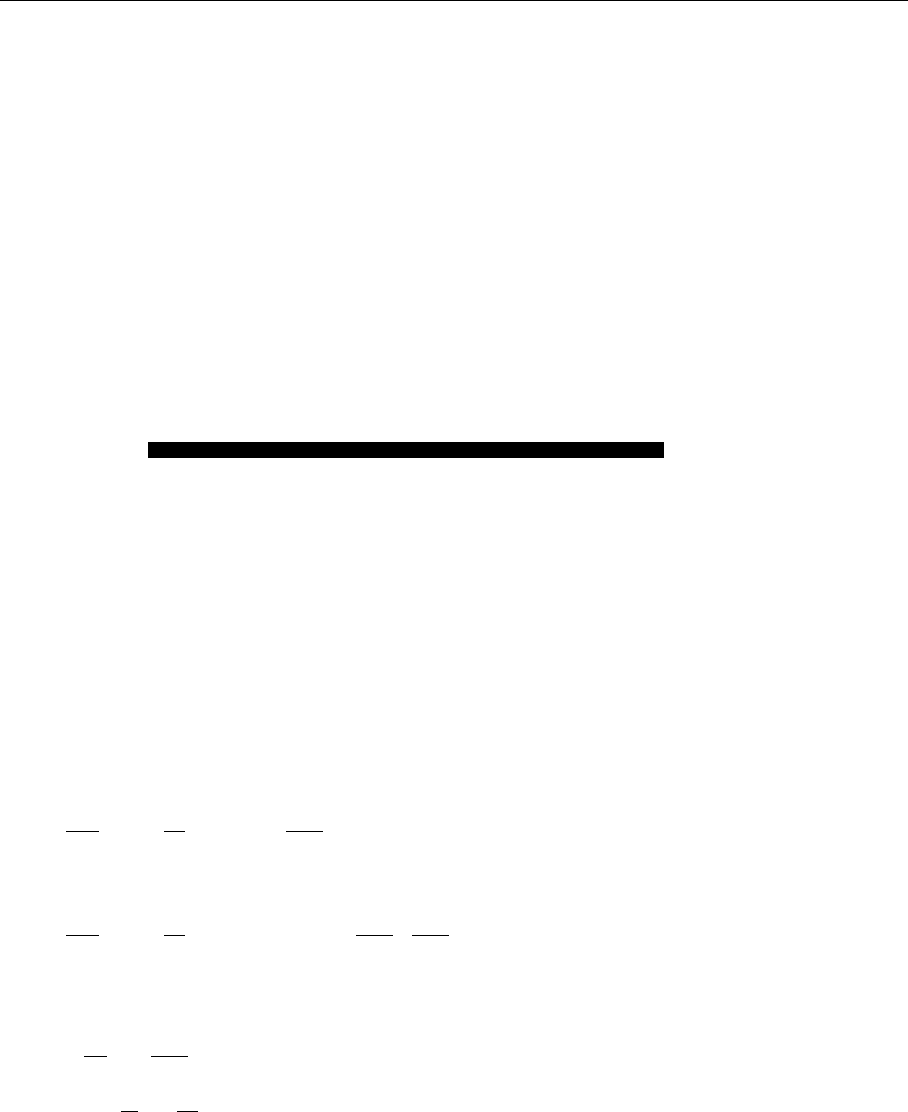
8.1 The Ground State of QCD 527
caused the model to be baptized the “Spaghetti vacuum” and guarantees Lorentz
invariance after averaging over sufficiently large spatial domains.
The picture of a dual superconductor is further supported by lattice cal-
culations for some simple systems. One can, for example, calculate the field
distribution around a static quark–antiquark pair. If the dual-superconductor pic-
ture is correct, the color electric field cannot extend into the QCD vacuum,
so that a string is created outside of which E vanishes. Figure 8.4 shows this
schematically as well as the results of a Monte Carlo calculation.
In conclusion there are detailed and quasiphenomenological models for the
QCD ground state. The “Spaghetti vacuum” is just one of them. All have in com-
mon that they lead to highly complicated nonperturbative field configurations
and that these have a constant negative energy density compared to the pertur-
bative vacuum. This energy density cannot simply be identified with the bag
constant. The fine structure of the QCD ground state should exhibit a length scale
of 1/λ
QCD
≈1 fm. Thus the average energy density is not relevant for a hadron;
and the precise microscopic structure must be known.
EXAMPLE
8.2 The QCD Ground State and the Renormalization Group
In this example we wish to show how (8.31) (or more accurately the real part of
(8.31)) can be derived from renormalization arguments in a very elegant man-
ner. We want to investigate the effective Lagrangian of an SU(2) gauge theory
for a constant color magnetic field. In lowest order this is simply −1/2H
2
.
Consequently the next order can be written as
L
eff
= F(H,µ,g), (1)
where µ denotes the renormalization in such a way that L
eff
becomes the free
Lagrangian for H = µ
2
. Since the effective Lagrangian must not depend on µ,
the renormalization group equation
µ
2
∂
∂µ
2
+β(g)
∂
∂g
+2γ(g)H
2
∂
∂H
2
F(H,µ,γ)=0(2)
must be fulfilled. The derivative of (2) with respect to H
2
is
µ
2
∂
∂µ
2
+β(g)
∂
∂g
+2γ(g) +2γ(g)H
2
∂
∂H
2
∂
∂H
2
F(H,µ,g) = 0 . (3)
Since ∂F/∂H
2
is a dimensionless quantity, it can only depend on H/µ
2
.There-
fore we define
t = ln
H
µ
2
,
∂
∂H
2
F(H,µ,g) = G(t, g), (4)
−(1−γ)
∂
∂t
+β
∂
∂g
+2γ
G(t, g) = 0 . (5)
528 8. Phenomenological Models for Nonperturbative QCD Problems
Example 8.2
This is the typical form of a renormalization group equation. Taking into account
the boundary condition
G
H=µ
2
= G
t=0
=−
1
2
(6)
yields
G(g, t) = exp
⎛
⎝
2
t
0
¯
γ(g, x) dx
⎞
⎠
G
(g, t), (7)
G
(g, 0) =−
1
2
, (8)
and
−(1−γ)
∂
∂t
+β
∂
∂g
G
(g, t) = 0 . (9)
We assign the new name g
0
to the constant g, because we want to introduce
a function g(t, g
0
) in the following:
G(g
0
, t) = exp
⎛
⎝
2
t
0
¯
γ(g
0
)dx
⎞
⎠
G
(g
0
, t), (10)
G
(G
0
, 0) =−
1
2
, (11)
and
−(1−γ)
∂
∂t
+β
∂
∂g
0
G
(g
0
, t) = 0 . (12)
Clearly (12) is solved by every function G
g(g
0
, t)
if
∂
∂t
g(g
0
, t) =
β
1 −γ
∂
∂g
0
g(g
0
, t). (13)
It is always possible to define G
g(g
0
, t)
and g(g
0
, t) in such a way that
∂g(g
0
, t)/∂g
0
=1 holds, such that (13) simplifies to
∂
∂t
g(g
0
, t) =
β
1 −γ
. (14)
Now (7) is evaluated by perturbative methods. In the case of small t we have
G
(g) ≈−1/2, and only the result for the anomalous dimension γ in the limit
of t → 0 is needed. Since we have not discussed the renormalization of gauge
theories in this volume, we can only cite the result. It turns out for a pure SU(2)
gauge theory that
γ and β are in lowest order proportional to each other:
γ =
β
2g
0
=
µ
2
g
0
∂g
∂µ
2
µ
2
=H
=−
1
g
0
∂g
∂t
t→0
=−
∂ ln g
∂t
t→0
. (15)
8.1 The Ground State of QCD 529
This relation allows us to evaluate (7):
G ≈
1
2
exp
(
−2{ln[g(g
0
, t)]−ln(g
0
)}
)
=−
1
2
g(g
0
, t)
g
0
−2
≈−
1
2
1 +
β
g
0
t
=−
1
2
−
1
2
g
2
0
(4π)
2
11 ×2
3
t , (16)
G ≈−
1
2
−
11g
2
0
48π
2
ln
H
µ
2
+O(g
4
). (17)
Therefore F assumes the form
F =−
11g
2
H
2
48π
2
ln
H
µ
2
−
1
2
=−
11g
2
H
2
48π
2
ln
H
H
0
. (18)
This derivation was first found by Savvidy.
2
Later Nielsen and Olesen discov-
ered in a lengthier calculation the nonstable states, which are overlooked by the
renormalization group method. This indicates that one has to be very cautious
when employing such abstract principles.
Without color electric fields, the energy density is
ε −ε(H = 0) =−F =
11g
2
H
2
48π
2
ln
H
H
0
.
EXAMPLE
8.3 The QGP as a Free Gas
In order to allow for simple calculations the QGP is usually described as
a free gas consisting of quarks and gluons. As we have already discussed, this
is theoretically not well founded at T ≈ T
c
. However, those calculations fre-
quently yield results which are qualitatively correct. Thus we simply add the gas
pressures of a free gluon gas
p
G
=16 ×
π
2
90
T
4
(1)
and of a free quark gas
p
Q
=12 ×
T
4
12
7π
2
30
+
µ
T
2
+
1
2π
2
µ
T
4
(2)
2
See S.G. Matinyan and G.K. Savvidy: Yad. Fiz. 25, 218 (1977).
Example 8.2

530 8. Phenomenological Models for Nonperturbative QCD Problems
Example 8.3
and identify the result with the bag pressure B. In the case p
G
+ p
Q
> B the
QGP region is supposed to expand and one should be able to derive the critical
temperature from
B = p
G
+ p
Q
= T
4
cr
'
37π
2
90
+
µ
T
cr
2
+
1
2π
2
µ
T
cr
4
(
(3)
for every value of µ. Assuming B = (145 MeV)
4
yields the result shown in
Fig. 8.9. This now has to be compared with Fig. 8.5. Apparenty there is a rough
qualitative but no quantitative agreement for the phase boundaries. One has
T(µ = 0)
T
µ =
4
3
T
max
=
)
155
113
= 1.4 for lattice calculations
102 MeV
91 MeV
=1.1 for the free gas .
(4)
Since the position of the phase boundaries is quite insensitive to theoretical
subtleties, one can expect that the free gas treatment of QCD leads for more sen-
sitive quantities, to results which are wrong by much more than 30%. Examples
of such quantities are the total number of kaons or lambda particles created.
8.2 The Quark–Gluon Plasma
In Sect. 7.1.16 we discussed that lattice calculations show a phase transition at
a critical temperature T
c
∼100 −200 MeV (Figs. 7.10 and 7.12). Such a phase
transition is typical for non-Abelian gauge theories. It has been studied exten-
sively for SU(2) and SU(3) but should exist for all SU(N) groups. If it could
be experimentally investigated in detail, such studies would definitely improve
our understanding of some of the basic properties of QCD. The hope is that in
high-energy collisions of heavy ions this new high-temperature phase can in-
deed be produced for sufficiently long times and in a sufficiently large volume
to allow experimental studies. While it is generally agreed that at high enough
energies the new phase will be reached in the center of the collision system, the
interpretation of possible experimental signals is still very much debated.
The interest in the quark–gluon plasma (QGP) phase transition is further in-
creased by the fact that it is assumed to have played a crucial role in the early
universe. As the universe cooled it was the last phase transition to occur and
might therefore have left recognizable traces in the present day structure of the
universe.
Another interesting point is that the QCD vacuum is a highly nontrivial state,
as is the vacuum of the standard model in general. In fact, the existence of
