Горский Н.М. Практикум по математической статистике

Подождите немного. Документ загружается.

Задача 6.

Рассматривается уровень результатов сдачи вступительных

экзаменов по математике в академию за несколько лет. Средний

процент сдавших экзамены за этот промежуток времени оказал-

ся равным 55%. В 2000 г. из экзаменовавшихся 100 абитуриен-

тов экзамены по математике выдержали 62 человека. Проверьте

гипотезу о том, что это довольно высокий процент, т. е. 2000 г.

был «удачным годом» в

области математики для этой академии.

Возьмите α = 0,01.

Ответ: Нулевая гипотеза H

: Р = 0,55;

: Р>0,55. Критиче-

ская область (0,666; +∞).

Статистическое решение: При 1%-ном уровне значимости

мы не можем сделать вывод о том, что абитуриенты 2000 г.

имеют лучшую по сравнению с предыдущими годами подготов-

ку по математике.

Задача 7.

Игральная кость подброшена 900 раз. Выпадение шестерки

наблюдалось 140 раз. Проверьте правильность игральной кости.

Воспользуйтесь двусторонним тестом для уровней значимостей

α = 0,05 и α = 0,01.

Ответ: Нулевая гипотеза

: Р = 1/6. Допустимая область

выпадений шестерок: 150 ±21,9; 150 ±28,8.

Задача 8.

В случайной выборке, состоящей из 900 человек с темными

волосами, 150 имеют голубые глаза. Предположим, что доля

голубоглазых людей среди всего населения известна и равна

0,25. Проверьте гипотезу о том, что доля темноволосых среди

людей с голубыми глазами меньше, чем доля голубоглазых сре-

ди всего населения. Возьмите α = 0,05.

Ответ: Нулевая гипотеза H

: р = 0,25; H

: р<0,25. Критиче-

ская область (−∞; 0,226).

Статистическое решение: Голубоглазых людей среди тем-

новолосых меньше, чем во всем населении.

Задача 9.

Известно, что 5% всех застраховавших свою жизнь умирает

по достижении 60 лет. В группе из 1000 человек этого возраста,

работающих в строительстве, умерло 68. Проверьте гипотезу

о том, что застрахованные люди, работающие в строительстве,

чаще умирают в 60 лет, чем все остальные застрахованные.

Ответ: Нулевая гипотеза Н

: р = 0,05; Н

: р > 0,05. При

α = 0,05 критическая область — (0,0614;+∞). При α = 0,01 кри-

тическая область — (0,066;+∞).

Статистическое решение: Люди, работающие в области

строительства, в 60 лет более склонны к смерти, чем остальное

население.

Задача 10.

Считается, что завод, производящий за неделю 1000 единиц

некоторого вида продукции, работает удовлетворительно, если

в среднем доля бракованных изделий при контроле качества не

превышает 3%.

Допустим, в течение некоторой недели контролером было

забраковано 38 изделий. Стоит ли директору завода провести

более полную проверку качества изделий производственной ли-

нии или же следует отнести высокий процент

дефектной про-

дукции этой недели на счет случайных изменений в условиях

производства? Воспользуйтесь односторонней проверкой гипо-

тезы с 5%-ным уровнем значимости.

Ответ: Наблюдаемое значение р

= 0,038, критическое зна-

чение р

кр

= 0,0389.

Статистическое решение: Число бракованных изделий 38

недостаточно при 5%-ном уровне ошибки для того, чтобы оста-

новить выпуск продукции. Директору завода следует продол-

жить выпуск товаров, однако в следующую неделю ему необхо-

димо провести второе наблюдение за качеством товаров. Если

и тогда окажется, что число бракованных изделий близко к 38,

то производственная линия

должна быть тщательно проверена.

Задача 11.

Фирма, производящая новый вид лекарства, объявила, что

оно излечивает от гриппа менее чем за 4 дня и его эффективность

равна 95%. В случайной выборке из 300 человек, заболевших

гриппом и принимавших это лекарство, 272 поправились менее

чем за 4 дня. Было ли заявление фирмы состоятельным? Приме-

ните односторонний критерий с 1%-ным уровнем значимости.

Ответ: Нулевая гипотеза

: Р = 0,95; альтернативная

: Р < 0,05. Критическое значение 0,9067 < 0,921.

Статистическое решение: Гипотеза Н

отклоняется, т. е.

заявление фирмы не подтверждено.

Задача 12.

Было произведено 10 измерений диаметра оси пропеллера.

При этом оказалось, что среднее

= 6,20 мм, исправленное

стандартное отклонение s = 0,05 мм. Найдите границы 95%-ного

и 99%-ного доверительных интервалов истинной величины

диаметра.

Ответ: а) 6,20 ±0,00967; б) 6,20 ±0,0139.

Задача 13.

Пропеллер из задачи 12 поместили в условия с высокой

температурой и провели еще 7 измерений диаметра его оси.

Среднее на этот раз оказалось равным 6,25 мм, а стандартное

отклонение — 0,05 мм. Можно ли из этого сделать вывод при

5%-ом уровне значимости, что диаметр оси пропеллера сущест-

венно увеличивается в пространстве с высокой температурой?

Ответ: Выборочное значение t

= 2,036, правосторонняя

критическая область, критическое значение t

кр

= 1,943. Нулевая

гипотеза отклоняется, так как t

кр

Статистическое решение: Диаметр оси пропеллера увели-

чивается при нагреве.

Задача 14.

Проведено шесть измерений времени реакции насекомого

на некоторый возбудитель: 0,20; 0,22; 0,19; 0,21; 0,20; 0,21с.

Найдите границы 95%-ного и 99%-ного доверительных интер-

валов среднего времени реакции для всей совокупности измерений.

Ответ: а) 0,205±0,011; б) 0,205±0,0172.

Задача 15.

Торговый контролер, в задачу которого входит контроль за

правильной массой отдельных товаров, отобрал десять стограм-

мовых пакетов с кофе и взвесил содержимое каждого из них. Он

получил следующие результаты (в граммах): 94; 95; 92; 102;

97;95; 102; 96; 92; 97.

Вычислите

и s.

Контролер хочет проверить, будет ли средний вес µ су-

щественно меньше, чем µ

= 100. Сформулируйте соответст-

вующие нулевую и альтернативную гипотезы.

3) Приняв α = 0,025, найдите критические значения Z и T

статистик. Какое из них нужно использовать для проверки на-

шей гипотезы?

Найдите выборочные значения z

или t

и, сравнив полу-

ченное значение с z

кр

или t

кр

, сделайте вывод о том, примет ли

контролер гипотезу или отвергнет ее.

Постройте доверительный интервал и объясните смысл

результата.

6) Если окажется, что 95 < µ <100, то магазину будет сде-

лано замечание. Однако если µ < 95, то магазин будет оштрафо-

ван. Какова вероятность того, что наше значение х происходит

из генеральной совокупности с µ = 95? Должен ли контролер,

располагая указанной выше информацией, оштрафовать магазин

или только сделать ему замечание?

Контролер хочет отобрать такую выборку, для которой

вероятность ошибки второго рода относительно альтернативной

гипотезы Н

: µ = 95 была бы равна β = 0,005. Чему должен быть

равен объем этой выборки?

Задача 16.

Считается, что новое антикоррозийное покрытие имеет эф-

фективность 99%, если среди 20 испытанных образцов нет ни

одного с признаками коррозии. В противном случае эффектив-

ность покрытия принимается равной 90%. Пусть р — вероят-

ность появления признаков коррозии у одного образца. Предпо-

ложим, что образцы обрабатываются и испытываются незави-

симо друг от друга. Рассмотрим нулевую гипотезу Н

: Р = 0,10;

альтернативная Н

: Р = 0,01. Какая статистика критерия должна

использоваться для проверки нулевой гипотезы? Найдите кри-

тическую область и область принятия гипотезы. В чем состоят

и чему равны ошибки первого и второго рода?

Ответ: Число образцов с признаками коррозии имеет би-

номиальное распределение В (20, Р). Критическая область —

,,,20}.

кр

{0};V =

кр

\{12VV

Ошибка первого рода: принима-

ется решение, что антикоррозийное покрытие имеет эффектив-

ность 99%, в то время как его эффективность составляет 90%.

Ошибка рода: принимается решение, что антикоррозий-

ное покрытие имеет эффективность 90%, в то время как его эф-

фективность составляет 99%. Вероятность ошибки первого рода

α = 0,122, вероятность ошибки второго рода β = 0,182.

второго

тическая область

{2, 3, , 10}.V

Задача 17.

Большая партия изделий может содержать некоторую до-

лю дефектных. Поставщик утверждает, что эта доля составляет

5%; покупатель предполагает, что доля дефектных изделий

равна 10%. Условия поставки: из партии случайным образом

отбирается и проверяется 10 изделий; партия принимается на

условиях поставщика, если при проверке обнаружено не более

одного дефектного изделия; в противном случае партия

при-

нимается на условиях покупателя. Сформулируйте эту задачу

в терминах теории проверки статистических гипотез. Каковы

статистика критерия, область ее значений, критическая об-

ласть? Какое распределение имеет статистика критерия? В чем

состоят проверяемая и альтернативная гипотезы? В чем состо-

ят ошибки первого и второго рода и каковы их вероятности?

Кому более выгодны

условия проверки и почему?

Ответ: Число дефектных изделий. Область значени

{0, 1, , 10};V = K кри

кр

Биномиальное

(

)

10,

. Н

: р = 0,05 верно утверждение по-

ставщика, Н

: Р = 0,10 верно утверждение покупателя.

Ошибка первого рода: партия принята на условиях покупа-

теля, в то время как верно утверждение поставщика.

Ошибка второго рода: партия принята на условиях постав-

щика, в то время как верно утверждение покупателя.

Вероятность ошибки первого рода α = 0,086, вероятность

ошибки второго рода β = 0,736.

Поставщику.

Задача 18.

Технология производства некоторого вещества дает в сред-

нем 1000 кг вещества в сутки со среднеквадратичным отклоне-

нием среднего, равным 80 кг. Новая технология производства

в среднем дает 1100 кг вещества в сутки с тем же среднеквадра-

тичным отклонением среднего. Можно ли считать, что новая

технология обеспечивает повышение производительности, если

α = 0,05 и α = 0,10? Вычислите вероятность

ошибки второго ро-

да при альтернативной гипотезе, утверждающей, что произво-

дительность при новой технологии возросла и составляет

1200 кг вещества в сутки.

Ответ: Нет. Нет. β = 0,198 и β = 0,112.

Задача 19.

В 10000 сеансов игры с автоматом выигрыш появился

4000 раз. Найти 95%-ный доверительный интервал для вероят-

ности выигрыша. Сколько сеансов игры следует провести, что-

бы с вероятностью 0,99 вероятность выигрыша отличалась от

частоты не более, чем на 1%?

Ответ: (0,39; 0,41); п ≥ 16231.

Задача 20.

Из большой партии резисторов одного типа и номинала

случайным образом отобраны 36 штук. Выборочное среднее

величины сопротивления при этом оказалось равным 9,3 кОм.

Используя двусторонний критерий при α = 0,05, проверить ги-

потезу о том, что выборка взята из партии с номиналом

10 кОм, если:

а) дисперсия величины сопротивления известна и равна

4 кОм

;

б) дисперсия величины сопротивления неизвестна, а ис-

правленная выборочная дисперсия равна 6,25 кОм

Решите задачу, используя доверительные интервалы для

среднего значения величины сопротивления.

Ответ: Нулевая гипотеза отклоняется. Нулевая гипотеза не

отклоняется. (8,647; 9,953); (8,454; 10,146).

Задача 21.

В соответствии с техническими условиями среднее время

безотказной работы для приборов из большой партии должно

составлять не менее 1000 часов со среднеквадратичным откло-

нением 100 часов. Выборочное среднее времени безотказной

работы для случайно отобранных 25 приборов оказалось рав-

ным 970 часам. Предположим, что среднеквадратичное откло-

нение времени безотказной работы для приборов в выборке сов-

падает

со среднеквадратичным отклонением во всей партии.

Можно ли считать, что вся партия приборов не удовлетво-

ряет техническим условиям, если а) α = 0,10; б) α = 0,01?

Решите задачу при условии, что оценка среднеквадратично-

го отклонения времени безотказной работы, вычисленная по

выборке, равна s = 115 часам.

Определить объем выборки, если альтернативная гипотеза

предполагает среднее время

безотказной работы 950 часов, а

вероятность ошибки второго рода не должна превышать 0,10.

Ответ: а) Да; б) нет. а) Нет; б) нет. а) п≥27; б) п≥53.

Задача 22.

С производственной линии, производящей сигареты, было

отобрано 900 сигарет, 45 из них оказались бракованными. Оце-

ните долю р дефектных сигарет во всей совокупности и найдите

90%-ный доверительный интервал для этой величины. Какой

объем выборки с производственной линии надо взять для того,

чтобы с вероятностью 95% можно было утверждать, что р не

отличается от выборочной доли р

более чем на 5%?

Ответ: р

= 0,05; 0,05±0,0119; п = 73.

Задача 23.

Выборка лампочек некоторого сорта А исследовалась на

продолжительность свечения. Время непрерывного свечения

выбранных лампочек (в условных единицах): 21; 32; 28; 14; 30;

27; 30.

Исследование выборки лампочек другого сорта В дало сле-

дующие результаты: 27; 35; 29; 16; 25; 28; 29; 34: 18; 30.

а) Найдите границы 99%-ного доверительного интервала

для средней продолжительности безотказной работы лампочек

каждого сорта µ

б) Найдите границы 95%-ного доверительного интервала

для разности µ

− µ

средней продолжительности безотказной

работы лампочек двух сортов.

Ответ: а) 99%-ный доверительный интервал для µ

26±3,71 2,401 = 26±8,91;

99%-ный доверительный интервал для µ

: 27,1±3,25 1,935 =

27,1±6,29;

б) 95%-ный доверительный интервал для разности средних

− µ

: −1,1±2,13 0,486 = −1,1±1,035.

Задача 24.

Химик делает шесть измерений концентрации серной кисло-

ты и обнаруживает, что средняя концентрация равна 9,234 со

стандартным отклонением 0,12. Проводя опыты с кислотой из

другой бутылки, он делает одиннадцать измерений, для которых

средняя концентрация равна 8,86, а стандартное отклонение рав-

но 0,21. Найдите границы: а) 90%-ных, б) 95%-ных, в) 99%-ных

доверительных интервалов разности средних величин

концентра-

ции серной кислоты в двух бутылках. Были ли наполнены бутыл-

ки одной и той же кислотой?

Ответ: а) 90%-ный доверительный интервал для разности

средних величин концентрации: −0,374±0,164;

б) 95%-ный доверительный интервал для разности средних

величин концентрации: −0,374±0,2;

в) 99%-ный доверительный интервал для разности средних

величин концентрации: −0,374±0,277. Бутылки наполнены раз-

ной смесью.

Задача 25.

Покрышки, произведенные на заводе А, исследовались на

износ (в км пройденного пути). При этом оказалось, что средний

пробег равен 25000 км, s = 1200 км. При тех же условиях испы-

тывались покрышки, изготовленные на заводе В. Средний про-

бег равен 23500 км, а s = 1000 км. Найдите 99%-ный довери-

тельный интервал разности средних для продолжительности

безотказной работы покрышек, изготовленных на двух заводах.

Сделайте вывод о разнице в износе шин.

Ответ: 99%-ный доверительный интервал для разности

средних величин износа шин: 1500±2998. При заданном уровне

значимости разница в износе шин незначима.

1.10. Задачи для самостоятельного решения

(без ответов)

Задача 26.

Вычислить вероятность получить не менее 20 хороших изде-

лий при заказе 23 изделий, если брак составляет примерно 10%.

Задача 27.

Для случайной выборки, включающей 549 человек, занятых

в строительстве, средний еженедельный доход равен 22,25 фунта

стерлингов, а стандартное отклонение — 6,60 фунта стерлингов.

Постройте 95%-ный и 99%-ный доверительные интервалы для

среднего еженедельного дохода для всех занятых в строительстве.

Задача 28.

Вычислите среднее число работающих в семье и стандарт-

ное отклонение. Постройте 95%-ный доверительный интервал

для среднего числа работающих в семье.

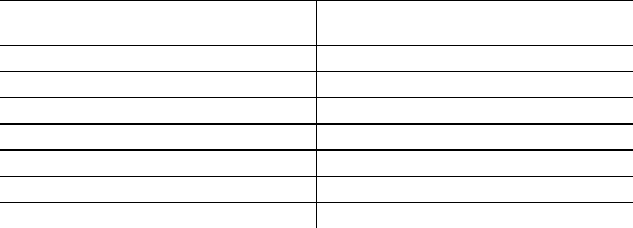
Число работающих Число семей

0 1356

1 2724

2 2250

3 613

4 186

5 42

6 и более 13

Задача 29.

Сотруднику некоторого университета поручено каждые три

года давать оценку средних расходов студентов на питание. Эта

оценка публикуется в университетской газете и используется

для определения размера стипендий и дотаций нуждающимся

студентам. Сотрудник решил взять некоторую выборку из об-

щего числа студентов и попросить студентов, попавших в вы-

борку, отмечать свои расходы

на питание в течение двух недель

осеннего семестра. Затем он решил собрать данные об общих

расходах от каждого из студентов и вычислить

и довери-

тельный интервал для µ.

а) Выборку какого объема следует взять для получения до-

верительного интервала шириной 0,4 долл. с уровнем значимо-

сти 0,05? Из предыдущего опыта известно, что s = 2 долл.

б) Оказалось, что выборочное среднее равно 28 долл. Вы-

числите доверительный интервал.

в) Сколько в среднем расходует студент на питание в

тече-

ние академического года (35 недель)?

г) Сведения о расходах на питание должны быть опублико-

ваны в виде точечной оценки. Считаете ли вы, что полученный

доверительный интервал достаточно мал для того, чтобы можно

было считать

точечной оценкой

Задача 30.

Средний возраст глав семей для случайной выборки из 3704

семейств равен 51,07 года, а стандартное отклонение — 16,98