Горский Н.М. Практикум по математической статистике
Подождите немного. Документ загружается.


Среднеквадратичным (стандартным) отклонением называ-
ется корень квадратный из исправленной выборочной дисперсии:
2
.SS=
Стандартной ошибкой средней называется стандартное от-
клонение выборочной средней
.
x
S
S
n
=
Значения этой статистики иногда используются в отечест-
венной и очень час то в зарубежной литературе по математиче-
ской и при
и по
нормальн
иями
кладной статистике.
При обработке статистической информации широко исполь-
зуют распределение статистик, выч сляемых выборке из
о распределенной генеральной совокупности. Эти рас-
пределения связаны с распределен
2
χ
, Стьюдента и Фи-
шера. Для них мы будем использовать следующие обозначения:
Z — случайная величина, имеющая стандартное нормальное
распределение
(
)
0, 1N
,
()
2
k
χ
2
χ
— случайная величина, имеющая распределение
с k степенями свободы,
(
)
Tk
— случайная величина, имеющая распределение
Стьюдента с k степенями свободы,
()
12
,
F
kk
— случайная величина, имеющая распределение
Фишера с k
1
и k
2
степенями свободы.
Квантилью порядка р распределения случайной величины Х на-
зывается действительное число
p
x
, удовлетворяющее уравнению
(
)
.
p
PX x p
<
=
Квантили порядка р основных распределений обозначаются
соответственно
(
)
2
.,,ztfkk
χ
12
,,
pppp
При выборках небольшого объема т оценки могут
цениваемых параметров, поэтому
очечные
существенно отличаться от о
11

их х
ра
я параметра
θ называется
инт
обычно дополняют интервальными оценками, которые а-
ктеризуют точность.
Доверительным интервалом дл
ервал
(
)
**
12
θ ,θ
со случайными границами
*
1
θ и
*
2
θ , который с
заданной доверительной вероятностью
(надежностью) γ = 1−α
накрывает неизвестное и значение етра
θ
: стинное парам
(
)
**
12
θ <θ < θ =1 - α,P
где
α — уровень значимости.
Нижняя и верхняя границы доверительного интервала
*
и
*
1
θ
определяются по результатам аблюдений и, следовательно,
явля
2
θ н
ются случайными величинами.
Часто применяются односторонние доверительные интерва-
лы, границы которых определяются из условий
(
)
*
и
(
)
*
θP
2
< θ =1 α
−
1
θ <θ =1 α.P
−
интервалами.
лее
Эти интервалы называются, соответственно, левосторонни-
ми и правосторонними доверительными
Симметричный доверительный интервал определяется бо-
простым соотношением
(
)
(
)
** *
θεθ < θε θθ ε1 α.PP
−
<+=−<=−
Величина
ε
называется точностью. Точность
ε
— это поло-
вин
центах.
ти
-
ному доверительному интервалу (точности ε) и объему выборки п;
а длины доверительного интервала.
Уровень значимости α и надежность γ = 1 − α иногда зада-
ются в про
Выбор доверительной вероятности определяется конкрет-
ными условиями. Обычно используемые значения γ = 1 − α рав-
ны 0,90; 0,95; 0,99 или 90%; 95%; 99%.
С интервальной оценкой связано решение трех пов задач:
1)
определение доверительного интервала (точности ε) по за-
данной доверительной вероятности γ = 1 − α и объему выборки п;
2)
определение доверительной вероятности
γ
= 1 −
α
по задан
12
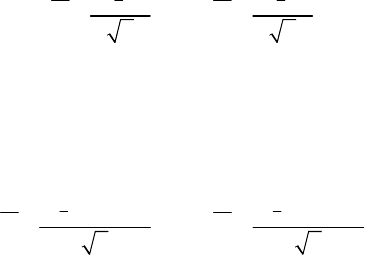
3)
опреде ому довери-
тельном тности
γ = 1 −
Распреде = 20,
можно полагать
оцен
будет при-
ближенным и существенно зависящим от объема выборки n.
и
1.2.1. Двусторонний доверительный интервал для оценки
параметра µ (генеральной средней) нормально распределенной
генеральной совокупности при известной дисперсии
ление объема выборки п по заданн
у интервалу (точности ε) и доверительной вероя
α.
ление выборочной средней, уже начиная с n
практически нормальным. Это позволяет при
ке генеральной средней использовать те же самые довери-
тельные интервалы, что и для параметров µ и
2
σ нормально
распределенного признака. Однако в этом случае он
1.2. Доверительные интервалы
для оценки параметров µ и σ
2
нормально
распределенной генеральной совокупност
αα
11
22
σσ
µ.
zz
XX
nn
−−
⋅
⋅
−<<+
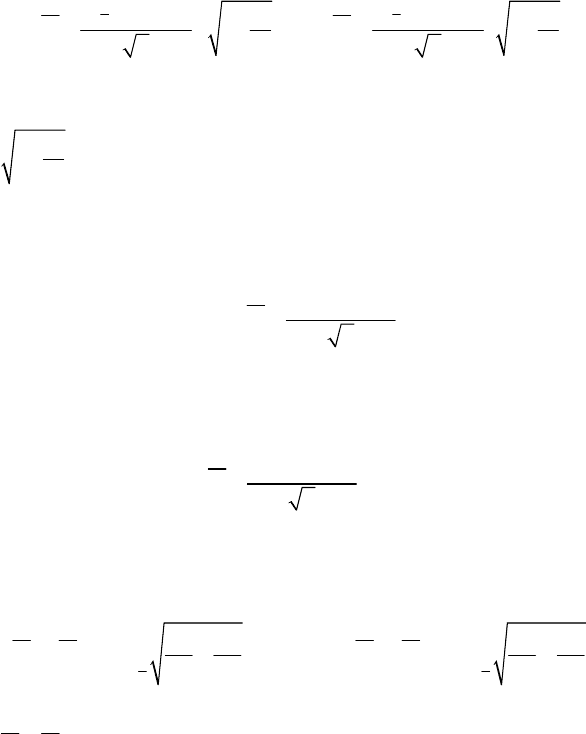
1.2.2. Двусторонний доверительный интервал для оценки
параметра µ (генеральной средней) нормально распределенной
генеральной совокупности при неизвестной дисперсии
α
1
2
µX
−
α
1
2
(1) (1)
.
tn S tn S
X
nn
−
−
⋅−⋅
<+
я оценки
параметра µ (генеральной средней) нормально распределенной
−<
1.2.3. Двусторонний доверительный интервал дл
13
генеральной конечной совокупности объема N по безвозвратной
выборке объема п при неизвестной дисперсии
αα
11
22
(1) (1)tn S tn S
1µ 1.
nn
XX
N
N
nn
−−
−⋅
−⋅−<<+⋅−
−⋅
Если объем безвозвратной выборки п много меньше, чем
объем генеральной совокупности N (n < 0,05N), то множитель
1
n
N
−
можно не использовать.
1.2.4. Левосторонний дове
параме µ
рительный интервал для оценки
генерал
тра (генеральной средней) нормально распределенной
ьной совокупности при неизвестной дисперсии
1 α
(1)
µ.
tn S
X
−
n
−
⋅
<+
1.2.5. Правосторонний доверительный интервал для оценки
параметра µ (генеральной средней) нормально распределенной
генеральной совокупности при неизвестной дисперсии
1 α
(1)
µ.
tn S
X
n
−
−
⋅
−
<
1.2.6. Двусторонний доверительный интервал для оценки
средних µ
−
µ двух нормально распределенных гене-
известных дисперсиях
разности
1 2
ральных совокупностей при
() ()
22 22
12
XX z−−
12 12
µµ ,XX z
σσ σσ
+<−<−+ +
2
рок;
12
α 12 α
11
12 12
22
nn nn
−−
где n , n — объемы выбо
1
12
,
X
X
— выборочные средние исследуемых генеральных со-
вокупностей;
22
,
12
σ
σ
— известные дисперсии генеральных совокупностей.
14
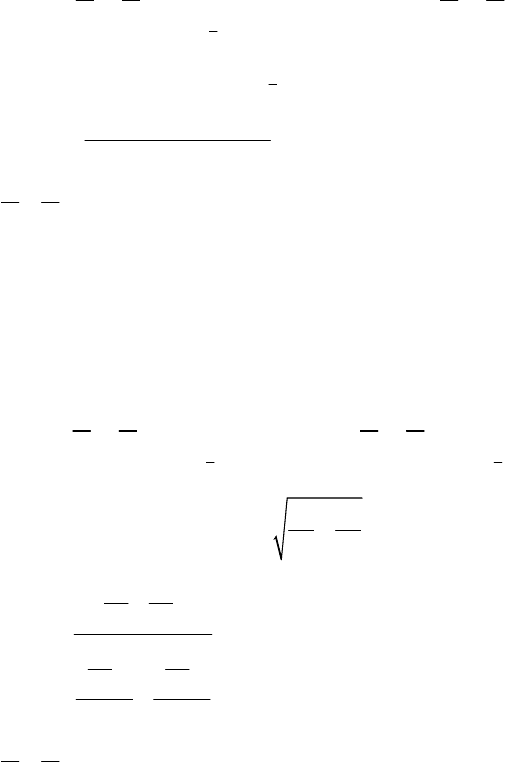
1.2.7. Двусторонний доверительный интервал для ценки
разности средних µ
1
−
µ
2
двух нормально распределенных гене-
ральных совокупностей при равных, но неизвестных дисперсиях
о
()
()
(
)
()
12 12
α 12 12
1
2
α 12
1
2
2µµ
2,
XX Stnn XX
St n n
−
−
− − +−<−< − +
+⋅ + −
(
)
(
)
22
112 2
2
12
11
;
2
где
nSnS
S
nn
−+−
=
+−
n
1
, n
2
— объемы выборок;
12
,
X
X
— выборочные средние сследуемых генеральных со-
вокупностей;
и
2
,SS
й при неравных и неизвестных дисперсиях
2
12
— исправленные выборочные дисперсии исследуемых
генеральных совокупностей.
1.2.8. Двусторонний доверительный интервал для оценки
разности средних µ
1
– µ
2
двух нормально распределенных гене-
ральных совокупносте
()
()
()
()
12 12
α 12 α
11
22
ν
µµ ν ,
−−
−− <−<−+XX St XX St
22
12
12
,=+S
nn
SS
2
22
12
12
22
22
12
12
12
ν
;где
SS
nn
SS
nn
⎛⎞
+
⎜⎟
⎝⎠
=
⎛⎞⎛⎞
⎜⎟⎜
11
nn
⎟
⎝⎠⎝⎠
+
−−
n , n
1 2
— объемы выборок;
12
,
X
X
— выборочные средние исследуемых генеральных со-
вокупностей;
15
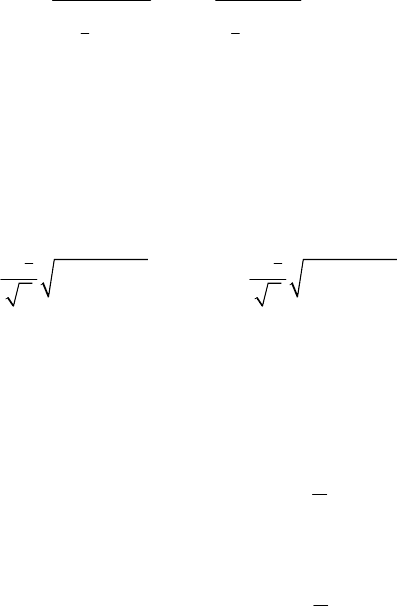
22
12
,SS — исправленные выборочные дисперсии исследуемых
генеральных совокупностей.
сии
2
нормально распределенной генеральной совокупности
при неизвестной средней
1.2.9. Двусторонний доверительный интервал для диспер-
σ
(
)
()
(
)
()
22
2
22
αα
1
22
11
σ .
11
nS nS
nn
χχ
−
−−
<<
−
−
1.2.10. Доверительные интервалы для оценки параметра Р
(доли признака) биномиального распределения
.
Если п>50, а выборочное значение относительной частоты р
*
удовлетворяет условиям пр
*
> 5 и п(
1
−
р
*
) > 5, то двусторонний
доверительный интервал для параметра Р биномиального распре-
деления имеет вид
() ()
αα
11
*****
22
11
zz
PPPPPP
nn
−−
−−<<+−
*
.P
Если n<50 или хотя бы одно из чисел пр
*
и п(1
−
р
*
) меньше
пяти, то для нахождения доверительных границ p
1
и
p
2
исполь-
зуют таблицы функции распределения для биномиального зако-
на: p
1
определяется как наибольшее значение Р, удовлетворяю-
щее неравенству
() ()
α
1,
2
n
nk
kk
n
kx
PX x Cp p
−
=
≥= − ≤
∑
а p
2
— как наименьшее значение Р, удовлетворяющее неравенству
() ()
0
α
1.
2
x
nk
kk
n
k
PX x Cp p
−
=
≤
=−
∑
≤
16
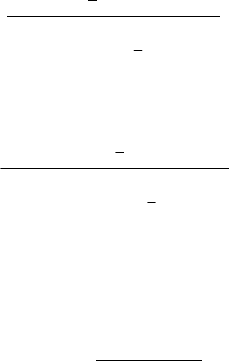
Точные доверительные границы могут быть также опреде-
лены при помощи формул:
(
)
()
α 12
2
1
α 12
2
,
,
1,
xf mm
p
nx xfmm
⋅
=
−++⋅
где
(
)
12
2, 2 1;mxm nx==−+
(
)
(
)
()()
α 12
1
2
2
α 12
1
2
1,
,
1,
xfkk
p
nx x f kk
−
−
+
=
−+ +
где
()
(
)
12
21, 2kxknx=+ =−
.
квантилями распределения Фишера
При вычислениях удобно использовать соотношение между
()
()
α 12
1 α 21
1
, .
,
fnn
f
nn
−
=
1.3. Построение точечных и интервальных оценок
для модельных задач
1.3.1. ЗАДАЧА ОБ ОЦЕНКЕ МАССЫ ИНДЕЕК
Построение двустороннего доверительного интервала
при неизвестном стандартном отклдля среднего онении.
ния масс (в фунтах): 12; 7; 9; 5; 4; 8; 17; 2; 11; 14; 13; 9.
Определение объема выборки
Среди студентов, изучавших в некотором колледже курс ста-
тистики, был сын фермера. На занятиях преподаватели говорили
ему, что в задачах, связанных с промышленным производством,
различные оценки делаются на основании очень небольших вы-
борок. Он решил оценить общую массу 5000 индеек на ферме
своего отца с помощью небольшой случайной выборки. Взвесив
вошедших в
эту выборку индеек, он получил следующие значе-
17
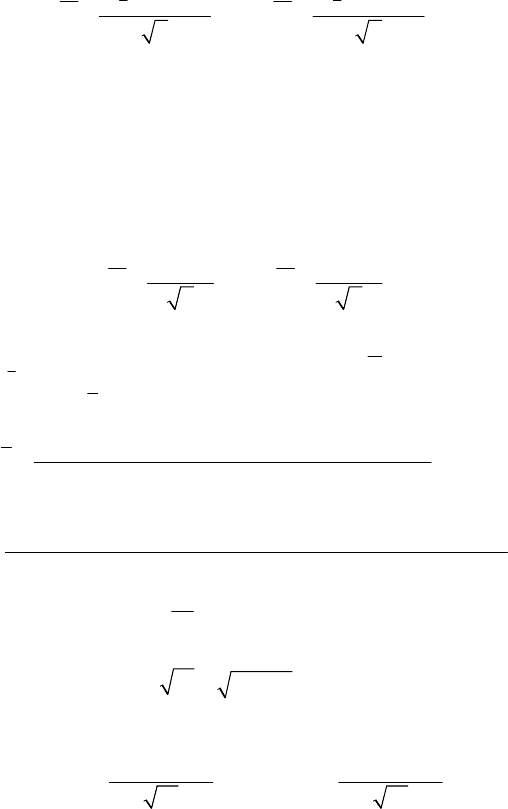
После этого он воспользовался следующей формулой для
вычисления двустороннего доверительного интервала:
αα
11
22
µ.XX
nn
(1) (1)tn S tn S
−−
−
⋅−⋅
е объема генеральной сово-
куп ,05N.
Действительно, n = 12 < 0,05·5000.
Приняв α = 0,05, он получил доверительны интервал
−<<+
Эту формулу он взял потому, что распределение индеек по
массе было близко, по его мнению, к нормальному распределе-
нию, величина стандартного отклонения
σ
неизвестна, а объем
выборки n = 12 был много меньш
ности N = 5000, т. е. было выполнено условие n < 0
й
2,201 2,201
µ,
−<<+
SS
XX
nn
α
1
2
α
( ) 2,201 1 11 γ 1 0,975.
2
где для иtk kn
−
==−==−=
Вычислив
x
и s
12 7 9 5 4 8 17 2 11 14 13 9
9,25;
12
x
++++++ ++ + + +
==
2
222222 22 2 2 2
2
2
12 7 9 5 4 8 17 2 11 14 13 9
11
12
9,25 19,295;
11
s
++++++ ++ + + +
=−
−⋅ =
2
19,295 4,39 ;ss== =
он получил
2,201 4,39 2,201 4,39⋅⋅
9,25 µ ;
12 12
−<−
9,25<
18
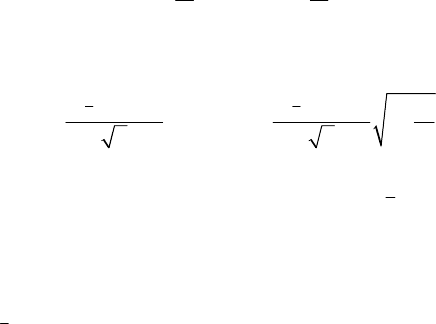
9,25−2,79<µ<9,25+2,79.
То есть 95%
-ный доверительный интервал имеет вид
6,46<
µ
<12,07.
Разумеется, отец только посмеялся, посмотрев на такой ре-
зультат, и сказал, что он может без всяких выборок гораздо точ-
нее оценить средний вес индейки µ, для чего ему достаточно
просто взглянуть на своих птиц. Сын фермера, если бы он более
внимательно изучал математическую статистику, мог догадать-
ся, что при таком
большом разбросе веса птицы от 2 до 17 фун-
тов и при среднеквадратическом отклонении 4,3 фунта объем
выборки должен быть значительно большим. Тем не менее отцу
очень хотелось получить доверительный интервал шириной
один фунт, поскольку т л бы стоянии более точно
это
до-
верительный интервал
огда он бы в со
оценить свой доход.
Сын догадался, что интервал шириной один фунт —
X
−
0,5 < µ <
X
+ 0,5
и состави уравнение для получения объема выборки
,
л
αα
11
22
(1) (1)
0,5
или
tnS tnS
−−
1 0,5.
n
N
nn
−
−
=
Он решил, что не стоит полагать
−=
1
2
(1)2,201,tn
α
−
−
=
по-
скольку
12n ≠ . Даже при своем ограниченном опыте статисти-
ческих исследований он понимал, что объем выборки будет
больше 30. Поэтому он подставил в уравнение
α 0,975
1
2
( 1) ( ) 1,960.tn t
−
−= ∞=
После этого он стал думать над
тем, по какой формуле определять объем выборки n. Второй
формулой сл дуе ет воспользоваться в том сл е, когда
n > 0,05 5000, т. е. n > 250. Сын фермера решил, что в сомни-
тельном случае лучше потратить
уча
больше времени на вычисле-
ния, чем получить неправильный ответ. Неправильный ответ
19
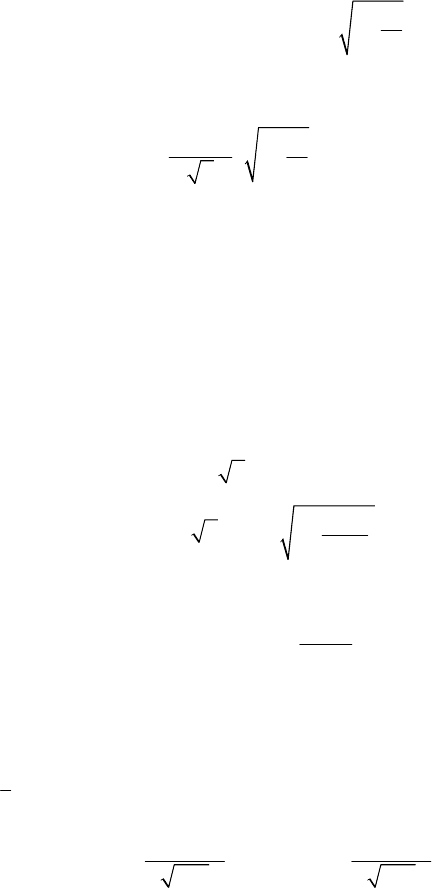
будет означать, что ему придется обследов ь большую выбор-
ку, на что понадобится гораздо больше времени, чем на решение
урав
ат
нения, включающего коэффициент
1
n
N
−
.
Таким образом, окончательно уравнение для определения
объема выборки n приобрело вид
1, 96
10,5.
Sn
N
n
⋅
⋅− =
Тогда ему стало ясно, что придется использовать значение
s = 4,39, вычисленное по уже отобранной им выборке из 12 ин-
деек. Он понял, что именно это обстоятельство имеет более об-
щее и n, не зная σ или, по
крайней мере, оценки S. Во всех последующих выборочных ис-
следованиях, в
которых ему придется искат n, он должен будет
сначала отобрать некоторую небольшую выборку, но не для то-
го, ч того,
чтоб
выборки.
части на
значение. Нельзя найти объем выборк
ь
тобы вычислить по ней доверительные пределы, а для
ы найти s, без чего он вообще не сможет определить объем
,n
он получил
Умножив обе
0,5 8,6 1 .
5000
n
n⋅=⋅−
После озведения в квадра в т уравнение приобрело вид
73,96
0,25 73,96 ;
5000
nn
⋅
=−⋅
n = 279 или 280.
К счастью, студент ещ л 12 индеек, которых он
взве
е не выпусти
шивал, обследуя свою первую выборку, так что ему при-
шлось взвесить еще «только» 268 индеек. В результате он полу-
чил
10,6x =
и s = 4,2, откуда
1, 96 4, 2 1, 96 4, 2
10,6 10,6 ,
µ
⋅⋅
−<<+
280 280
20
