Горский Н.М. Практикум по математической статистике

Подождите немного. Документ загружается.

1.8.11. ЗАДАЧА О ЦЕЛЕСООБРАЗНОСТИ ПРОВЕДЕНИЯ РЕКЛАМЫ

Проверка гипотезы о равенстве средних при неизвестных дисперсиях

Компания, в ведении которой находится большое число ма-

газинов, разбросанных по всей стране, решила рассмотреть во-

прос о целесообразности кампании по рекламе некоторого про-

дукта. Выполнение предварительных исследований было поруче-

но отделу сбыта готовой продукции. Чтобы добиться макси-

мальной сравнимости результатов, проверка должна была произ-

водиться в одно и то же

время в двух сопоставимых регионах

(а не в одном и том же регионе, но в разное время). Это устранило

бы возможные эффекты, обусловленные теми или иными сезон-

ными или циклическими факторами.

В регионе А проводили соответствующую рекламную кам-

панию, тогда как в регионе В работа шла обычно. Через некото-

рое

время в регионе А случайно были выбраны 22 магазина

и собраны данные о количестве проданного товара.

Соответствующие суммы оказались следующими (в долларах):

391, 367, 360, 429, 389, 420, 375, 344, 421, 385, 443, 379, 379, 356,

405, 369, 425, 345, 372, 395, 406, 382.

Сведения по 25 магазинам, взятым из региона В, оказались

следующими (в долларах): 319, 302, 311, 279, 317, 344, 333, 326,

290, 348, 245, 323, 332, 302, 300, 286, 309, 338, 334, 293, 285, 310,

312, 325, 291.

Результаты дальнейших вычислений следующие:

для региона А

388x=

1 1

15887

; 757 ; 27,5 ;

s s= =

для региона В

13424

310 ; 559 ; 23,6 .xs s====

22 2

Прежде всего проверим гипотезу о равенстве дисперсий:

левая альтернативная гипо-

теза

Этап 1. Ну гипотеза

01 2

:σσ;H =

:σσ.H ≠

11 2

Этап 2. α 0,05.

Этап 3. Объемы выборок п

= 22 и п

= 25.

Этап 4. Статистика критерия

()

12 1

~1,1,где

Fn n S S

=−− >

оннего

кри

Этап 5. Область принятия гипотезы

H для двустор

терия

()

1, 1 .

fn n

α 12

−

−−

(

)

(

)

кр 0,975 0,975

22 1, 25 1 21, 24 2,34.ff f=−−= =

Этап 6. Сформулируем правила проверки гипотезы.

а) Гипотеза Н

должна быть отвергнута на уровне значимо-

сти

, если вычисленное значени f

попадет в критическую об-

ласт

тие ся, если вычисленное з

ь, т. е. f

≥2,34.

не отвергается (прини

б) Гипотеза

мается) или ее приня-

откладывает начение f

принадлежит

области принятия гипотезы, т. е. f

<2,34.

Этап 7. Вычисляем выборочное значение статистики Фишера:

757

1, 35f == ≈

559

решение. Этап 8. Принимаем статистич се кое

Поскольку

вкр

1,35 2,34, . ,т. е

то нулевая гипотеза о

равенстве дисперсий не отклоняется (принимается).

Проверяем гипотезу о равенстве средних при неизвестных,

но равных дисперсиях.

Этап 1. Нулевая гипотеза альтернативная ги-

потеза

Этап 2. Уровень значимости

01 2

:µ µ ;H =

11 2

:µ µ .H >

α 0,05.

Этап 3. Объемы выборок п

= 22 и п

= 25.

Этап 4. Статистика критерия

()

TTn

−

⋅+

−

()()

112 2

где

nSnS−+−

принятия гипотезы для правосторонне-

го критерия

+−

Этап 5. Область

(

)

1 α 12

2tt n n

−

+−

(

)

(

)

кр ,95 0,95

Этап 6. Сформулируем правила проверки гипотезы.

а) Гипотеза Н

22 25 2 45 2,01.tt t=+−= =

должна быть отвергнута на уровне значимо-

сти

имается) или ее приня-

тие

принятия гипотезы, т. е. t

<2,01.

Этап 7. Вычисляем выборочное значение статистики Стью-

дента:

, если вычисленное значение t

попадет в критическую об-

ласть, т. е. t

≥2,01.

б) Гипотеза Н

не отвергается (прин

откладывается, если вычисленное значение t

принадлежит

области

25,52

⋅+ ⋅ +

388 310

7,51,

11 11

−

== ≈

()()

() ()

112 2

1 1 22 1 757 25 1 559

где

nsns

−+− −⋅+−⋅

25,52.

222252nn

≈

+− +−

Принимаем статистическое решени .

Посколь у

то нулевую ги

потезу о

том, что

вкр

7,51 2,01, . ,т. е tt

несущественно отличается от

, следует отвергнуть.

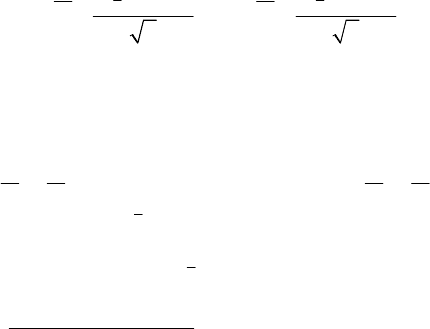
Для оценки дохода от продаж после проведения рекламной

кампании можно вычислить двусторонний доверительный ин-

тервал для

При уровне значимости

µ . α 0,05

он вид имеет

αα

(1) (1)

µ.

tnS tnS

−−

−<<+

Если еобходимо оценить доп ьный доход (н олнител при-

быль) для сравнения с расходам на проведение кампании, то

можно вычислить двусторонний доверительный интервал для

разности

При уровне

µµ− . значимости α 0,05

он имеет вид

()

(

)

()

12 12

α 12 12

α 12

2µµ

XX Stnn XX

St n n

−

− − +−<−< − +

++−

(

)

(

)

112 2

nSnS

−+−

С помощью этой информации руководство компании может

принять обоснованное решение о том, следует ли проводить ре-

кламную кампанию в общенацион

где

+−

ри-

мере задачи о булочке с изюмом.

Пусть некий хлебозавод выпускает сладкие булочки с изю-

мом, причем по государственному стандарту на 1000 булочек

полагается 10000 изюмин. Подозреваем, что часть изюма могут

украсть, и хотим это проверить. Для контроля мы можем купить

одну или несколько булочек и сосчитать, сколько там изюмин.

В данном случае речь идет о контроле по готовому изделию.

альном масштабе.

1.8.12. ЗАДАЧА О БУЛОЧКЕ С ИЗЮМОМ

Проверка гипотезы о параметре λ распределения Пуассона

Рассмотрим проблему проверки качества продукции и пла-

нирования деятельности правоохранительных органов на п

1. Формулировка статистических гипотез

Есть разные способы перемешивать тесто. Например, мож-

но засыпать изюм в одном месте, а помешать в другом. Когда же

начальство отвернется — выгрести обратно весь неразмешан-

ный изюм. Мы не будем рассматривать такие ситуации и пред-

положим, что перемешивание изюма в тесте происходит равно-

мерно. Выделим в тесте

объем, отвечающий купленной нами

булочке. Он будет составлять 0,001 от всего объема теста. Орга-

низуем схему испытаний: каждое испытание будет состоять

в том, что мы будем каждую изюминку бросать (мысленно)

в тесто и смотреть, попала ли данная изюминка в нашу булочку

(успех) или не попала (неудача). При равномерном перемеши-

вании теста

вероятность успеха равна 0,001, а всего испыта-

ний — n = 10000 (по числу изюмин). Конечно, испытания не

вполне независимы: если вся первая тысяча испытаний закон-

чится успехом, то в булочке не останется места для новых изю-

мин, и все остальные испытания закончатся неудачами. Однако

при равномерном перемешивании такая ситуация практически

невозможна. Предположим приближенную

независимость и

принимаем приближение Пуассона, причем

λ 10000 0,001 10np

⋅= ⋅ =

−

(среднее число изюмин на одну булочку).

Если предположить, что доля

всего изюма укра-

дена, то

(0 1)aa≤≤

λ λ() 10(1 ).aa

Пусть нулевая гипотеза состоит в том, что ничего не укра-

дено

. Эту гипотезу естественно объявить основной.

Альтернативные гипотезы имеют вид

H . Число изюмин в куп-

ленной нами булочке при верной альтернативной гипотезе

подчиняется закону Пуассона с параметром

:Ha=

λ( ) 10(1 ).

−

2. Возможные стратегии проверок

Предположим, что хлебозаводов много, то есть правоохра-

нительные органы сталкиваются со статистической ситуацией.

И задача состоит в том, чтобы выявить и изъять нарушителей

закона, ни в коем случае не тронув честных людей и не остано-

вив производство булочек с изюмом. Первичным материалом

являются жалобы покупателей на то, что в булочках нет или

очень мало изюма. Можно встать на крайнюю позицию: как

только поступает достоверная жалоба на отсутствие изюма —

саж

ачу

выбранной булочке не окажется изюма (Х = 0), дается формулой

ать пекаря. Посмотрим, что из

этого получится.

Если никакого воровства нет, то вероятность того, что в науд

(0) 10 4

λ(0) 10

(0|) 0,510.

0! 0!

PX H e e

−

−−

== = ≈⋅

Вероятность того, что хотя бы в одной из 1000 булочек не

окажется изюма, нужно подсчитывать как вероятность суммы

событий, т. е. суммировать вероятности событий, вычитать ве-

роятности их пересечений и т. д. Оценки показывают, что веро-

ятностями пересечения событий, т. е. таких, что в продаже ока-

залось две и более булочек

пренебреч

без изюма, можно ь и за

вероятность

овится. При массо-

вом производ збежно и не

обяз

суммы приближенно принять сумму вероятностей,

хотя события и совместны:

1000 0,5 10 0,05.

−

⋅⋅ =

Таким образом, если предположить, что каждый из

1000 покупателей, купив булочку без изюма, тут же пишет жа-

лобу, то вероятность того, что в правоохранительные органы

будет хоть одна жалоба, равна 0,05. Следовательно, вероят-

ность, что честный пекарь останется на свободе, равна 0,95. Бу-

лочки пекутся каждый день, так что вероятность остаться на

свободе

в течение года равна (0,95)

365

≈ e

– 0,05⋅365

≈ e

– 18

, что очень

близко к нулю. Через год ни одного пекаря не останется на сво-

боде и производство булочек с изюмом остан

стве какое-то количество брака неи

ательно говорит о недобросовестности.

3. Проверка статистических гипотез

Построим критическое множество для гипотезы H

. Против

гипотезы H

может свидетельствовать лишь малое количество

изюмин x в купленной для исследования булочке, но никак не

большое. Следовательно, критическая область должна быть од-

носторонней, точнее, левосторонней, и иметь вид S = {x: x≤k},

где k предстоит выбрать из соображений уровня значимости

(или функции мощности). Уровень значимости в данном слу-

чае — гарантия честного работника от ложного подозрения —

надо брать малым. Попробуем

= 0,01. Из статистических таб-

лиц

a = 0,1

(укр

о украл одну

деся

зн

распределения случайных величин по закону Пуассона по-

лучаем для α = 0,01 значение k = 3 (P {x ≤ 3 ⎢H

} ≈ 0,01).

Приведем отдельные значения функции мощности. Для

адена одна десятая всего изюма) P {x≤ 3⎟H

0,1

}≈0,02, а для

a = 0,5 (украдена половина изюма) P {x≤ 3⎟H

0,5

}≈0,26.

Моральная шкала и шкала качества готового изделия резко

не совпадают. По моральной шкале они резко различны: чест-

ный и вор. Но при a = 0,1 среднее число изюмин в булочке сни-

жается лишь на 10%. Соответственно, если честному человеку

предоставить гарантию не выше 0,01, то того, кт

тую всего изюма, мы

обвиняем с вероятностью 0,02, а ук-

равшего половину изюма — с вероятностью 0,26.

Таким образом, проверка статистических гипотез не позво-

ляет создать достаточно резкое различие между ситуацией H

при a ≠ 0, что связано с неэффективностью контроля по

единичному готовому изделию. Для отличия гипотез H

0,1

нужно отличить значения пуассоновского параметра λ = 9 и

λ = 10. Отклонение ачения случайной величины от ее матема-

тического ожидания λ для распределения Пуассона составляет

величину порядка

λ . Понятно, что значения λ = 9 и λ = 10

разли удно. Можно, конечно, взять для исследования не

одну, а 100 булочек. Тогда нужно отличить λ = 1000 от λ = 900

при

чить тр

λ 30,=

что гораздо легче. Но подсчет изюмин в ста бу-

лоч

ого раз больше

вероятности обвинения честного человека. На этом можно сыг-

рать, если использовать статистические методы.

ках выглядит очень непривлекательно с точки зрения трудо-

вых затрат на такой подсчет.

Гипотезы H

0 и

0,5

отличаются более заметно: вероятность

обвинения, если украдена половина изюма, во мн

4. Какую пользу можно извлечь

из статистических методов?

Вышеприведенные расчеты ясно показывают, что для окон-

чательного решения вопроса о наличии правонарушения стати-

стические методы непригодны (они могут составлять лишь

часть доказательств). Должны применятся более прямые мето-

ды, но их применение трудоемко. Если предположить, что, ска-

жем, 80% всех работников честны и лишь

20% воруют, то в 80%

случаев усилия будут потрачены впустую.

Рассмотрим применение статистических методов проверки

лишь для предварительного отбора объектов (по-английски это

называется screening, т. е. просеивание). Будем проверять гипотезу

не на малом, а на большом уровне значимости, например, α = 0,15,

делая при этом вывод не о наличии или отсутствии правонаруше-

ния

, но только о желательности или нежелательности непосредст-

венной проверки. В этом случае из статистических таблиц для

слу-

чайных величин, распределенных по закону Пуассона, получаем

для α = 0,15 значение k = 6, причем P {x≤ 6 ⎢H

}≈0,13. Это означа-

ет, что если вместо чисто случайного выбора объекта для непо-

средственной проверки принять более сложную процедуру (снача-

ла случайно выбирается хлебозавод, потом из его продукции бе-

рется одна булочка и проверка производится лишь в том случае,

когда число изюмин в ней х ≤ 6), то проверка будет напрасной

лишь с вероятностью 0,8⋅0,13 ≈ 0,104. Иначе говоря, лишь 10%

усилий будут потрачены впустую.

Этот оптимистический вывод нужно правильно понять.

Речь идет о сравнении двух следующих ситуаций: 1) в начале

рабочего дня случайно выбирается хлебозавод, на который со-

трудники едут с проверкой; 80% рабочих дней в этом случае

будет потеряно впустую; 2) в начале рабочего дня

случайно вы-

бирается хлебозавод, берется булочка из его продукции, и если

число изюмин в ней х≤6, то сотрудники едут с проверкой на

этот завод, а если x>6, то занимаются другим полезным делом

(в этом случае день не потерян).

1.9. Задачи для самостоятельного решения

(с ответами)

Задача 1.

Фирма провела полевые испытания шести образцов одина-

кового оборудования и не обнаружила среди них неисправных.

Как часто можно ожидать, что в выборке объема будут отсутст-

вовать неисправные образцы, если:

а) ожидаемая доля неисправных образцов равна 5%?

Ответ: 0,7351.

б) ожидаемая доля неисправных образцов равна 10%?

Ответ: 0,5314.

Задача 2.

Лабораторные образцы эмалированных пластин были под-

готовлены для испытаний на скручивание. Все они находятся

в одинаковых условиях контроля. Предыдущие опыты подска-

зывают нам, что в этом конкретном эксперименте не выдержат

испытания около 5% образцов.

Какова вероятность того, что в выборке объема 10 ока-

жется:

а) нуль дефектов?

Ответ:

( 0) 0,5987.PX

≈

б) один дефект?

Ответ:

( 1) 0,3151.PX

≈

в) менее трех дефектов?

Ответ:

(0 3) 0,9884.PX

≤

<≈

2) Как много образцов надо включить в выборку, чтобы

в ней с вероятностью 95% оказалось не менее пяти бездефект-

ных образцов?

Ответ: Найдем n из неравенства

( 5) 0,95.PX n

≤

−≥

При n = 6 получаем

(1)0.97PX .

≤

≈

Задача 3.

По заявлению некоторой фирмы вероятность того, что дан-

ное покрытие устойчиво против коррозии (что определяется пу-

тем стандартных испытаний), равна 0,95. Было отобрано 20 не-

зависимых образцов.

а) Если эти покрытия столь хороши, как утверждает фирма,

то как много брака можно ожидать?

Ответ: Одно.

б) Какова вероятность того, что будет обнаружен более

чем

один случай брака?

Ответ: 0,2642.

Задача 4.

Пусть вероятность получения качественного листа при на-

несении на него покрытия равна 0,90.

а) Сколько бракованных листов следует ожидать в выборке

объема 50?

Ответ: 5.

б) Какова вероятность того, что в выборке объема 50 ока-

жется не более пяти плохих листов?

Ответ: 0,3839.

в) Какова вероятность того, что окажется менее трех плохих

листов?

Ответ: 0,1117.

Задача 5.

В партии объема 100 пять плохих образцов и пять образцов

на грани возможного использования, которые после доработки

можно использовать. Какова вероятность того, что в выборке

объема 30 окажется самое большее один образец на грани воз-

можного использования и не будет плохих?

Ответ:

30 29 1

90 90 5

100

CCC

⋅

Объясните ответ. Попробуйте вычислить.