Горский Н.М. Практикум по математической статистике
Подождите немного. Документ загружается.


а) отношения семей, состоящих из одного человека, б) отноше-
ния семей, состоящих из 6 и более человек.
Число членов семьи
Число семей
в 1966 г., %
Число семей
в 1968 г., %
1 14,0 16,2
2 30,8 30,2
3 21,1 20,6
4 18,7 18,3
5 8,7 8,8
6 и более 6,7 5,9
Всего: 100 100
Общее число опрошенных семей 3274 7184
Задача 63.
На каждом из двух имеющихся на заводе станков произво-
дят новые изделия одного типа. При пробном пуске из 350 изде-
лий, изготовленных на станке А, при проверке по принципу го-
ден — не годен 15 оказались дефектными. Среди 320 изделий,
изготовленных на станке В, оказалось всего 8 дефектных. Мож-
но ли, приняв уровень значимости равным
α
= 0,05, ожидать,
что в продукции, производимой на сравниваемых станках, ока-
жется одинаковая доля дефектных изделий?
91
Список рекомендуемой литературы
1. Калинина В. Н., Панкин В. Ф. Математическая статистика.— М.:
Высшая школа, 1998.— 336 с.
2. Общий курс высшей математики для экономистов. Учебник/ Под
ред. В. И. Ермакова.— М.: ИНФРА-М, 2003.— 656 с.
3. Сборник задач по высшей математике для экономистов. Учебное
пособие / Под ред. В. И. Ермакова.— М.: ИНФРА-М, 2003.—
575 с.
4.
Шикин Е. В., Чхартишвили А. Г. Математические методы и моде-
ли в управлении.— М.: Дело, 2000.— 440 с.— (Серия «Наука
управления»).
Список использованной литературы
1. Вайнберг Дж., Шумекер Дж. Статистика.— М.: Статистика,
1979.— 389 с.
2. Джонсон Н., Лион Ф. Статистика и планирование эксперимента
в технике и науке. Методы обработки данных.— М.: Мир, 1980.—
510 с.
3. Колкот Э. Проверка значимости.— М., Статистика, 1978.— 128 с.
4. Мелник М. Основы прикладной статистики.— М.: Энергоатомиз-
дат, 1983.— 416 с.
5. Теннант-
Смит Дж. Бейсик для статистиков.— М.: Мир, 1988.—
208 с.
6. Тернер Д. Вероятность, статистика и исследование операций.—
М.: Статистика, 1976.— 431 с.
7. Тутубалин В. Н. Теория вероятностей и случайных процессов.—
М.: Изд-во МГУ, 1992.— 400 с.
92
Раздел II
ВЫЧИСЛИТЕЛЬНЫЙ ПРАКТИКУМ
ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
2.1. Образец задания по математической статистике
Вариант № 777
Выборка 1
1 1 2 4 3 1 6 1 2 2
2 0 0 3 0 2 4 1 2 1
1 1 2 1 2 0 3 2 1 0
1 2 1 1 4 2 1 3 1 1
3 1 4 0 3 1 3 6 8 5
Выборка 2
1,92 3,83 3,27 4,59 4,00 1,32 3,79 2,54 3,24 3,51
3,67 2,15 3,76 2,96 3,67 2,21 3,98 1,11 3,99 2,17
4,98 3,36 2,74 4,29 3,03 4,36 3,31 1,66 3,59 5,19
2,90 1,94 2,95 1,75 2,48 3,59 2,99 3,22 1,87 1,96
1,44 2,99 3,19 4,81 3,20 1,96 2,97 4,05 2,83 2,23
Для выполнения задания необходимо;
1. Определить тип исследуемого признака (дискретный или
непрерывный).
2. В зависимости от типа признака построить полигон отно-
сительных частот для дискретного случая или гистограмму для
непрерывного случая.
3. Построить эмпирическую функцию распределения (функ-
цию накопленных относительных частот).
4. Для выборки вычислить:
а) выборочное среднее,
93
б) исправленную выборочную дисперсию,
в) среднеквадратическое (стандартное) отклонение.
5. Для дискретного признака проверить гипотезу о соответ-
ствии выборочных данных распределению Пуассона с парамет-
ром λ = 2 с помощью критерия
2
χ
(хи-квадрат) на уровне зна-
чимости α = 0,05.
6. На основе анализа гистограммы и эмпирической функции
распределения непрерывного признака выбрать гипотезу о зако-
не распределения: нормальный или равномерный.
7. Для генеральной средней (математического ожидания)
и дисперсии непрерывно распределенного признака построить
двусторонние доверительные интервалы, соответствующие на-
дежности (доверительной вероятности) γ = 0,95.
8. Предположив,
что исследуемый непрерывно распределен-
ный признак имеет нормальное распределение, проверить гипоте-
зу о равенстве генеральной средней (математического ожидания)
значению µ = 3,00 на уровне значимости α = 0,01 при альтерна-
тивной гипотезе о том, что генеральная средняя µ > 3,00.
9. Предположив, что исследуемый непрерывно распреде-
ленный признак имеет нормальное распределение, проверить
гипотезу о равенстве
генеральной дисперсии значению σ
2
= 1,00
на уровне значимости α = 0,05 при альтернативной гипотезе о
том, что генеральная дисперсия σ
2
<1,00.
2.2. Образец выполнения задания
по математической статистике
Выполнение задания следует начинать с обработки дис-
кретного признака.
1. Определить тип исследуемого признака.
Значения, наблюдаемые в выборке 1, являются целыми чис-
лами, причем некоторые значения повторяются по несколько раз.
Вывод: экспериментальная выборка 1 является результатом
наблюдений над дискретной случайной величиной Х. Объем
выборки п = 50.
94

2. Упорядочив элементы выборки 1 по величине, построим
вариационный ряд: 0; 0; 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1;
1; 1
признака
та встр
; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 3; 4; 4; 4; 4;
5; 6; 6; 8.
Подсчитаем, сколько раз каждая из вариант встречается в
данной последовательности. Результаты подсчета запишем в
виде таблицы 1, первая строка которой содержит значения вари-
ант x
i
(различных значений исследуемого ), вторая —
их частоты n
i
(сколько раз данная вариан ечается в выбор-
ке) и третья — относительные частоты
*
i
i
n
p
n
=
(для их вычис-
ления каждый элемент второй строки нужно раздел ъем
выборки п, в нашем сл ае 50)
1
x
i
0 1 2 3 4 5 6 8
ить на об
уч на .
Таблица
n
i
6 18 11 7 4 1 2 1
*
i
i
n
p
n
=
0,12 0,36 0,22 0,14 0,08 0,02 0,04 0,02
Для контроля правильности записи находим сумму частот
n
i
— сумму элементов второй строки. Эта сумма должна быть
равна объему выборки n = 50:
(0; 0,12),
8
1
618117412150.
i
i
nn
=
==+++++++=
∑
При вычислении относительных частот округление резуль-
татов должно быть проведено так, чтобы их сумма была равна 1.
Полученную табл. 1 иногда называют статистическим ря-
дом.
На основании данных таблицы 1 строим полигон относи-
тельных частот. Для его построения на оси абсцисс находим
точки, соответствующие различным значениям вариант. В каж-
дой из этих точек
по оси ординат отложим соответствующие
значения относительных частот. Отмеченные точки соединим
отрезками прямой линии. Или, другими словами, в прямоуголь-
ной системе координат находим точки с координатами
95
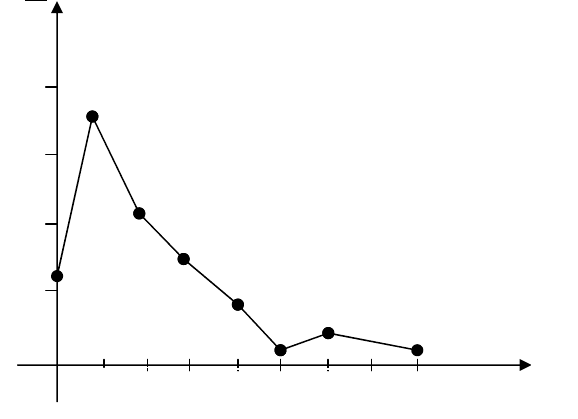
(1; 0,36), (2; 0,22), (3; 0,14), (4; 0,08), (5; 0,02), (6; 0,04),
(8; 0,02) и соединяем их отрезками прямой (рис. 1).
Рис. 1
0,4
0,3
0,2
0,1
0
n
i
n
i
p =
*
1 3
4
5
7
8
x
6
2
3. Построим эмпирическую функцию распределения для
дискретной случайной величины.
Наименьшее значение варианты равно 0, поэтому при х ≤ 0
случайная величина Х не может принять значение, меньшее х.
Следовательно, значения эмпирической функции распределения
F
*
(x) равны 0 при всех х ≤ 0. Если 0 < х ≤1, то неравенство Х < x
выполняется только для варианты х
1
= 0, которая встречается в
выборке с относительной частотой p
1
*
= 0,12, т. е. F
*
(x) = 0,12 при
0 < х ≤1. Если 1 < х ≤ 2, то неравенство Х < x выполняется уже для
двух вариант х
1
= 0 и х
2
= 1, которые встречаются в выборке с от-
носительными частотами p
1
*
= 0,12 и p
2
*
= 0,36. Для получения
значения эмпирической функции распределения F
*
(x) эти относи-
тельные частоты нужно сложить, т. е. F
*
(x) = 0,12 + 0,36 = 0,48
96
при 1 < х ≤2. Если 2 < х ≤3, то неравенство Х <x выполняется для
трех вариант х
1
= 0, х
2
= 1 и х
3
= 2, которые встречаются в выборке
с относительными частотами p
1
*
= 0,12, p
2
*
= 0,36 и p
3
*
= 0,22. Для
получения значения эмпирической функции распределения F
*
(x)
эти относительные частоты нужно сложить, т. е. F
*
(x) = 0,12 +
+ 0,36 + 0,22 = 0,70 при 2 < х ≤3 и т. д. В результате получаем, что
эмпирическая функция распределения (функция накопленных
относительных частот) для дискретной случайной величины име-
ет вид
()
*
0; 0;
0,12; 0 1;
0,48; 1 2;
0,70; 2 3;
0,84; 3 4;
0,92; 4 5;
0,94; 5 6;
0,98; 6 8;
1; 8 .
x
x
x
x
Fx x
x
x
x
x
≤
⎧
⎪
<≤
⎪
⎪
<≤
⎪
<≤
⎪
⎪
=
<≤
⎨
⎪
<≤
⎪
<≤
⎪
⎪
<≤
⎪
⎪
<
⎩
Построим график эмпирической функции распределения.
Для его построения на оси абсцисс находим точки, соответст-
вующие вариантам. В каждой из этих точек по оси ординат от-
кладываем соответствующие значения эмпирической функции
распределения. Левее точки х = 0 функция F
*
(x) принимает
только нулевые значения. Между точками х = 0 и х = 1 на высо-
те 0,12 проводим стрелку, направленную от 1 к 0. Конец стрелки
означает, что F
*
(0) = 0, а начало, что F
*
(1) = 0,12. Между точка-
ми х = 1 и х = 2 на высоте 0,48 проводим стрелку, направленную
от 2 к 1. Конец стрелки означает, что F
*
(1) = 0,12, а начало, что
F
*
(2) = 0,48 и т. д. Правее точки х = 8 проводим стрелку на высо-
те, соответствующей 1. Конец стрелки означает, что F
*
(8) = 0,98,
а во всех точках правее ее F
*
(x) принимает значение, равное 1
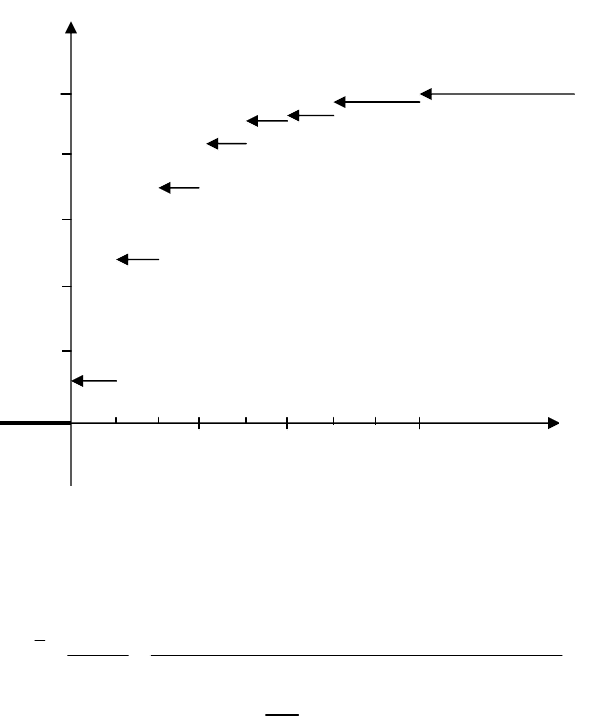
(рис. 2).
97
0
F
*
(x)
2 3 4 5
6
8
0,2
0,4
0,6
0,8
1,0
x
1
7
Рис. 2
4. Вычислим выборочные характеристики:
а) выборочная средняя
1
06 118 211 37 44 51 62 81
50
102
2,04;
50
n
ii
i
xn
x
n
=
⋅
+⋅ +⋅ +⋅+⋅+⋅+⋅+⋅
==
==
∑
=
98

б) исправленная выборочная дисперсия
22
2
2
11
iiii
ii
n
sx
==
==−⋅=
22 2 2 2 22 2
2
()
111
06118211374451628150
2,04
49 49
nn
xxn xn
nnn
⋅⋅ ⋅ ⋅ ⋅ ⋅⋅ ⋅
−
−−−
⋅+ ⋅ + ⋅ + ⋅+ ⋅+ ⋅ ⋅+ ⋅+
350
4,25 2,89;
49
−
⋅=
∑∑
в) выборочное среднеквадратичное (стандартное) отклоне-
ние равно
=− ≈
2
1, 70.ss==
5. Проверим гипотезу о соответствии выборочных данных
распределению Пу λ=ассона с параметром 2 с помощью крите-
рия
2
χ
(хи-квадрат) на уровне значимости α = 0,05.
Распределение Пуассона в общем случае имеет вид
()
λ
λ
!
.
k
PX k
k
e
−
==⋅
По статистическим таблицам или, вычисляя по соответст-
вующим формулам, как это сдел ниже, находим теоретиче-
ские вероятности:
ано
()
() ()
()
()
()
()
1! 1 0! 1
2
320,180;
3! 3 2! 3
e
PX e e PX
=
== =⋅ = =≈
0
2
2
10
22
21
0 0,135;
0!
2222
100,270;
PX e
e
PX e PX
−
−−
== = ≈
== =⋅ = ≈
21
22
32
22
22 2
210,270;
2! 2 1! 2
2222
PX e e PX
−−
−−
== =⋅ = =≈
99
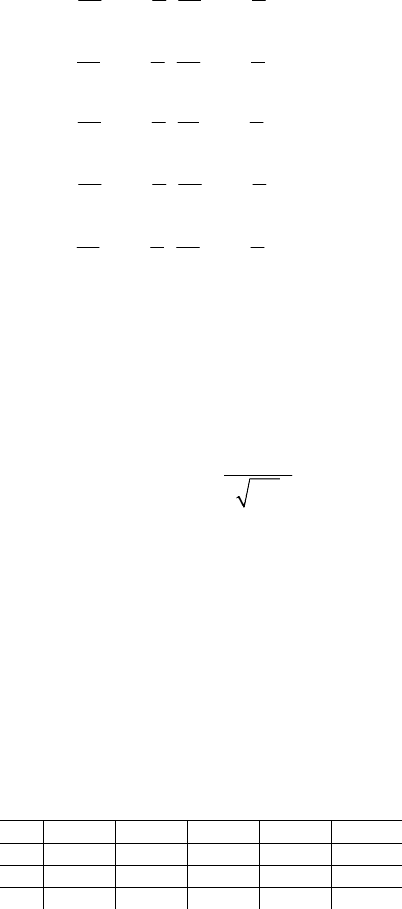
() ()
()
()
43
22
54
22
2222
4 3 0,090;
4! 4 3! 4
2222
540,036;
5! 5 4! 5
PX e e PX
PX e e PX
−−
−−
== =⋅ = =≈
== =⋅ = =≈
() ()
()
()
()
61
22
76
2222
6 5 0,012;
6! 6 5! 6
2222
7
PX e e PX
PX e
−−
== =⋅ = =≈
==
()
≈
22
87
22
6 0,003;
7! 7 6! 7
222
8 7 0,001.
!
e PX
PX e PX
−−
−−
=⋅ = =≈
⋅ = =
-
лени о
умножить на объем выборки и округлить до ближайшего цело-
го. Для исследуемой выборки найденные вероятности нужно
умножить на 50.
Использование критерия
2
8! 8 7 8
e
== =
Для нахождения ожидаемых (теоретических) частот появ
я исследуемого признака найденные вероятности нужн
2
χ
(хи-квадрат) основано на том
факте
, 1, 2, , ,
ii
, что случайная величина
i
ik
np
=
K
имеет
распределение, близкое к стандартному нормальному распреде-
лению
(
nnp−
)
0,1N
.
Для обеспечения необходимой точности нужно, чтобы час-
тота каждой группы была не менее пяти, поэтому значения для
к = 4, 5, 6 и 8 нужно объединить. Результаты запишем в виде
табл е
а р
ца 2
ицы, в первой строке которой выписаны наблюдаемы зна-
чения, объединенные в группы, во второй — наблюдаемые зна-
чения (сколько раз значение наблюдаемого признака приняло
данное значение).
В третьей строке запишем соответствующие
теоретические вероятности, в четвертой — тео етические зна-
чения частот (табл. 2).
Табли
2 3
≥4
x
i
0 1
n
i
6 18 11 7 8
p
i
0,135 0,270 0,270 0,180 0,145
np
i
7 14 14 9 7
100
