Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§ 2.8. Конечнозначные логики

141

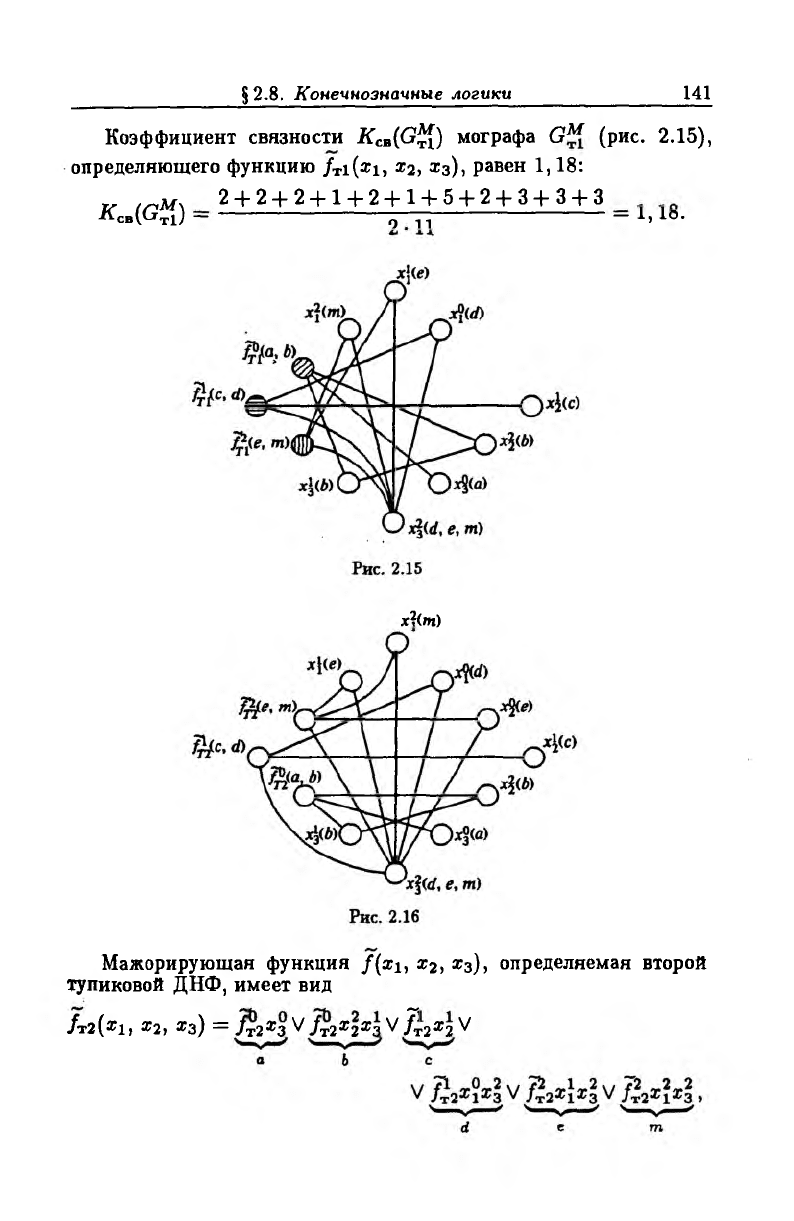
Коэффициент связности K CB(G£{) мографа G™ (рис. 2.15),

определяющего функцию / Ti(*i, х2, z3), равен 1,18:

К (ГЩ 2 + 2 + 2 + 1 + 2 + 1 + 5 + 2 + 3 + 3 + 3

Л св(Сгт1) — о 11 — 1,1о.

х?(т)

Мажорирующая функция f(x i, х2, хз), определяемая второй

тупиковой ДНФ, имеет вид

Ы х и х2, *з) = 7rf*3 V /*2*2*3 V 7т2*2 V

142 Гл. 2. Математическая логика

и соответствующий ей мограф G™ (рис. 2.16) имеет коэффициент

связности, равный 1,18:

K CB(G%) = 2 + 2 + 2 + 1 + 2 + 2 + 5 + 1 + 3 + 3 + 3 = ^ ^

Полученные тупиковые ДНФ функции f(x i, 13) имеют рав

ные сложности.

§ 2.9. Исчисление предикатов

Исчисления высказываний недостаточно для задания более

сложных логических рассуждений. По существу А;-значная ло

гика позволяет определить наличие того или иного свойства на

конечном множестве элементов; в случае бесконечных множеств

для установления определенного свойства у рассматриваемого аб

страктного понятия необходимо введение функций, аргументы ко

торых пробегают бесконечное число значений во множестве М.

Функция Р, принимающая одно из значений, 0 или 1, аргументы

которой пробегают значение из произвольного множества М, на

зывается предикатом Р в предметной области М. Число аргу

ментов предиката Р(х 1, х2, ..., *п) называется его порядком.

Предикат Р(х 1, х2) ■ ■., хп) определяет n-арное отношение R

в М: если P(xJ, х2, ..., х*) = 1, то (xj, х2, ..., х*) находятся в

отношении R, определяемом этим предикатом, и если P(*J, х2, ...

..., х*) = 0, то эти элементы не находятся в отношении R, т. е.

(*;, *5, . . g Д.

Для упрощения структуры сложных логических рассуждений

введем специальные обозначения для некоторых часто встречаю

щихся выражений. Условимся обозначать выражение “для вся

кого элемента х G М свойство R выполнено” как (Vz € M) (R(x) =

= 1), а выражение “существует по крайней мере один элемент

х € М, обладающий свойством R” — как (Эх € M)(R(x) = 1). В

выражениях (Va; € M)(i?(x) = 1) и (Зх € M)(R(x) = 1) обозначе

ния Ух и Зх будем соответственно называть квантором всеобщ

ности и квантором существования.

Определим индуктивно формулу исчисления предикатов ана

логично определению формулы исчисления высказываний. Будем

использовать запятые, скобки, символы исчисления высказыва

ний, предметные переменные хх, х2, ... (переменные, принимаю

щие значения из предметной области), предметные константы ai,

а2, ..., предикатные буквы Pi, Р2, ... и функциональные буквы

Л,/а,...

Определим понятие терма и элементарной формулы.

Определение терма:

1) всякая предметная переменная или предметная констан

та — терм;

§2.9. Исчисление предикатов 143

2) если / — функциональная буква и щ, rfe, ..., г}п — термы,

то /(гц, т?2, . . Vn) — терм;

3) любое выражение, полученное многократным повторением

правил 1), 2), является термом.

Если Р — предикатная буква, а щ, ..., rjn — термы, то

Р{Чи V2, Цп) — элементарная формула.

Определение формулы:

1) всякая элементарная формула является формулой;

2) если Л и В — формулы и х — предметная переменная, то

каждое из выражений Л о В (о — связка исчисления высказыва

ний) и (Ух € М)(А(х)) является формулой;

3) любое выражение, полученное многократным использова

нием правил 1), 2), является формулой.

В выражении (Va: € М)(А(х)) формула А(х) называется об

ластью действия квантора Vs.

Предметная переменная, входящая в формулу, называется

свободной, если она не следует непосредственно за квантором и не

входит в область действия квантора по этой переменной; все дру

гие переменные, входящие в формулу, называются связанными.

В пределе всякая формула без свободных переменных (замкнутая

формула) является высказыванием, которое истинно или ложно,

а всякая формула со свободными переменными задает некоторое

отношение в предметной области, которую иногда называют об

ластью интерпретации. Это отношение может быть истинно или

ложно в зависимости от значений свободных переменных.

В определении формулы в числе основных символов запись Зх

можно заменить на Vx(A(x)).

Квантор всеобщности можно рассматривать как обобщение

конъюнкции. Если предметная область конечна и с о сто и т и з эле

ментов n»i, т2, ..., тп„, то формула (Vx)(F(x)) равносильна конъ

юнкции F(m i) & F(m2) & .. .& F(m n), а квантор существования

можно рассматривать как обобщение дизъюнкции, при этом за

писи (3a:)(F(x)) и F(mi) V F(m 2) V ... V F(m n) равносильны.

Для бесконечных предметных областей кванторы играют роль

бесконечных дизъюнкций и конъюнкций.

Каждая формула F(Pi, Р2, ..., Рт, ®i, х2, • • •> хп) в исчисле

нии предикатов задает оператор, перерабатывающий систему пре

дикатов Pi, Р2, ..., Рт в предикат Ра от аргументов xi, х2,

• . хп, где все эти переменные в формуле являются свободными.

Две формулы, Fa(Pi, Р2, ..., Pm, *i, х2, ..., хп) и Fb(Pi, Р2, ...

• . Рт,х 1, х2, ..., хп), которые задают один и тот же оператор,

перерабатывающий систему предикатов Pi, Р2, ..., Рт в предикат

Pa(x 1, х2, ..., хп), будем называть эквивалентными и обозначать

Fa = Fb.

144

Гл. 2. Математическая логика

Переход ох формулы F к ее эквивалентной форме будем назы

вать, как и в исчислении высказываний, тождественным пре

образованием.

Основываясь на введенных понятиях, можно доказать следукъ

щие четыре тождества:

тождества двойственности

(Эх) (Р(*)) = (V !)(PW ), (Vx) (Р(х)) = (Э * )(Щ );

тождества для ж-операций (т. е. для конъюнкции и кван

тора всеобщности)

(Vx)(Fe(x) A Fb(x)) = (Vx)(F.(x) A (Vx)F6(*)),

(Vz)(Vy)(F(x, у)) = (Vy)(Vx) (F(x, y));

тождества для а-операций (т. е. для дизъюнкции и квантора

существования)

(3*)(Ftt(a?) V Fj(x)) = (3x)(Fa(x) V (3x)F6(*)),

(3*)(3y)(F(x, y)) = (3y)(3x)(F(x, y));

тождество вынесения константы

(Ex)(Fe о F6(x)) = Fa о (Ex)(F6(x)),

где (Ex) = (3x), (Vx); о = A, V; Fa — подформула, не содержащая

связанную предметную переменную х, которая в дальнейшем будет

называться константой относительно квантора (£х).

При вынесении константы из области определения квантора

существования подкванторное выражение предварительно приво

дят к виду дизъюнкции конъюнкцией; при вынесении константы

из области определения квантора всеобщности выражение приво

дят к виду конъюнкции.

Рассмотрим, например, вынесение константы G(y):

(Vx)((F(x) G(y)) V (H(x)oG(y))) =

= (Vx) (F(x) А Щу) V H(z)VG(y)) = (Vx) (F(x) A % ) V

V {Щх) А Щу))) = (Vx) (Щу) А НЩ V F(x)) =

= (V»)(Gfo) А (Я(х) -4 F(x))) = ( Щ ) A (Vx)(tf(x) -4 F(x)).

В рассматриваемом исчислении кванторы применены только

по предметным переменным. Формулы будут более выразитель

ными, если наряду с кванторами по предметным переменным ис

пользовать и кванторы по предикатным переменным.

Исчисление, в котором применяются только кванторы по пред

метным переменным, называется узким исчислением предика

тов; последнее можно преобразовать в расширенное исчисление

предикатов, добавив кванторы по предикатным переменным.

S2.10. Теория трасс

145

Определение формулы в расширенном исчислении предикатов

аналогично ее определению в узком исчислении; разница состоит

в том, что в п. 2) определения формулы переменная х может быть

как предметной, так и предикатной. Тождества двойственности

я--, сг-операций и вынесение константы в расширенном исчислении

предикатов тоже справедливы.

Рассмотрим вопрос выводимости в исчислении предикатов.

Расширим систему аксиом некоторого исчисления высказываний,

включенного в узкое исчисление предикатов, следующими аксио

мами:

(Vz)(G(x)-4 G(y))\ Н(у) -> (3*)Я(*).

Смысл этих аксиом следующий: если предикат G(x) истинен

для любого х, то он истинен и для любого у, и если предикат

Н (у) истинен для какого-нибудь у, то существует такой х, что

Н(х) истинен.

В узком исчислении предикатов два правила вывода (подста

новки и заключения) исчисления высказываний дополняют еще

тремя правилами.

Правило для V: если tpi -4 <£>2 выводима и в ip\ нет х в качестве

свободной переменной, а в ^ переменная х содержится в виде

свободной переменной, то формула ipi -4 V(z)<^2 также выводима.

Правило для 3: если ipi -4 щ выводима и х содержится в

качестве свободной переменной в щ и не содержится в качестве

свободной переменной <^2, то формула 3(x)ip\ -4 ip2 также выво

дима.

Правило переименования связанных переменных: если <pi —

выводимая формула и в i/>i имеется квантор всеобщности или

квантор существования, то одна связанная переменная в щ мо

жет быть заменена другой связанной переменной одновременно во

всех областях действия квантора и в самом кванторе; полученная

формула также выводима.

§ 2.10. Теория трасс

Выше было рассмотрено применение математической логики в

экспертных системах при геологоразведке полезных ископаемых.

Рассмотрим ее использование при оценке переходных процессов

в электронных системах, реализующих субмикронную техноло

гию, т. е. в системах, рабочая частота которых — сотни мегагерц

И выше. В этом случае ложная информация порождается неод

новременными переключениями входных каналов из-за задержек

сигналов в каналах связи.

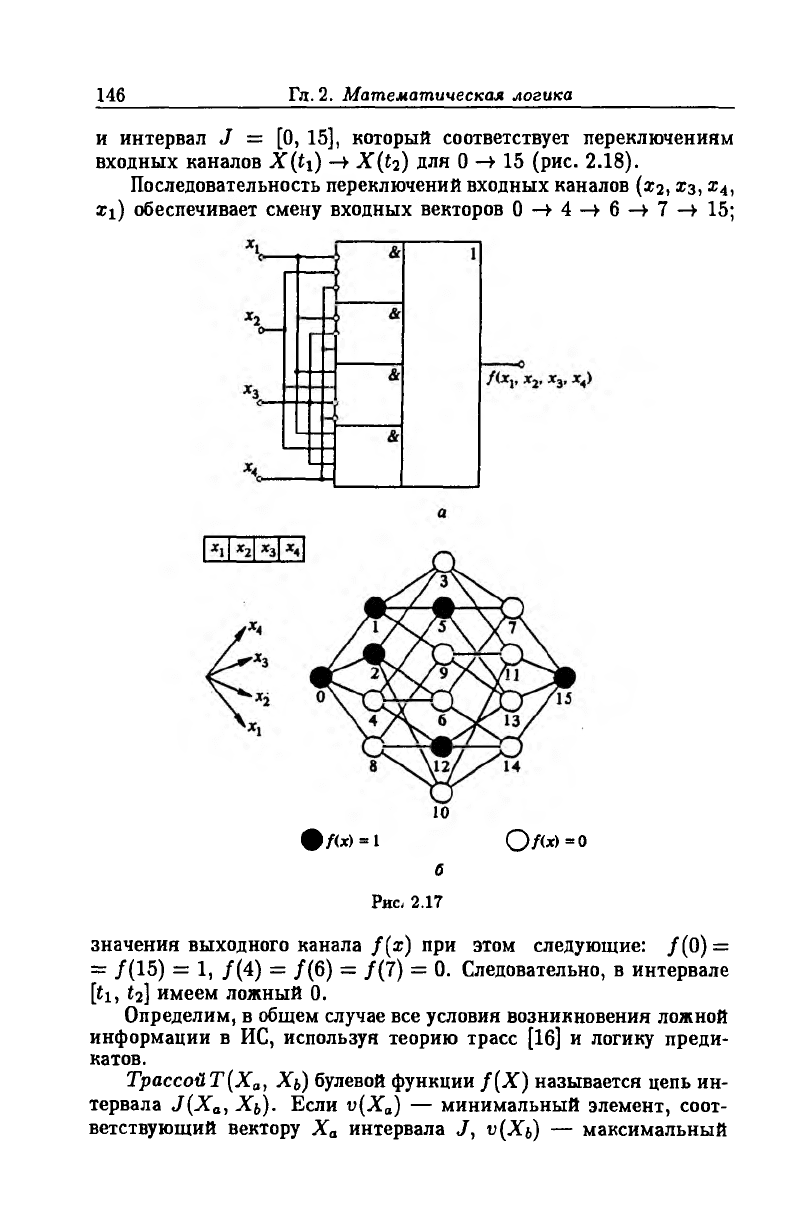
Рассмотрим интегральную схему (ИС) (рис. 2.17, а), реали

зующую булеву функцию (рис. 2.17,6)

/(* 1, *2, *з. xA)\i = V(0, 1, 2, 5, 12, 15),

146

Гл. 2. Математическая логика

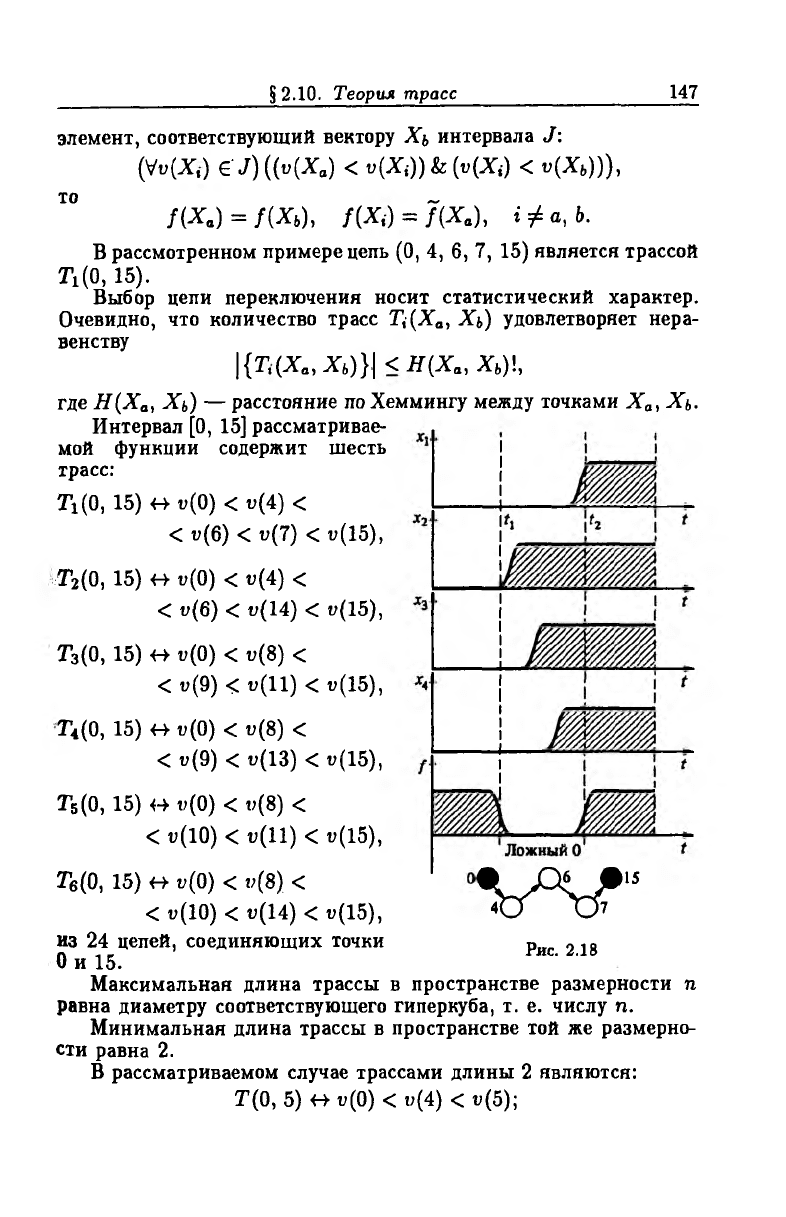
и интервал J = [0, 15], который соответствует переключениям

входных каналов X (tj) -4 X(t2) для 0 -4 15 (рис. 2.18).

Последовательность переключений входных каналов (х2, хз, xAi

*i) обеспечивает смену входных векторов 0-44-4 6-4 7-4 15;

#/(*) = ! О/<*)=0

Рис, 2.17

значения выходного канала f(x) при этом следующие: /(0) =

= /(15) = 1, /(4) = /(6) = /(7) = 0. Следовательно, в интервале

[ti, t2] имеем ложный 0.

Определим, в общем случае все условия возникновения ложной

информации в ИС, используя теорию трасс [16] и логику преди

катов.

ТрассойТ(Ха, Хь) булевой функции f{X) называется цепь ин

тервала J(Xa, Хь). Если v(Xa) — минимальный элемент, соот

ветствующий вектору Ха интервала «7, v(Xb) — максимальный

§2.10. Теория трасс

147

элемент, соответствующий вектору Хь интервала J:

(Vu(X,) €J){(v(Xa) < v(Xi))k(v(Xi) < v(Xb))),

то ~

f(Xa) = f(Xb), /(* ,) = /(X e), i^a,b.

В рассмотренном примере цепь (0, 4, 6, 7, 15) является трассой

2\(0, 15).

Выбор цепи переключения носит статистический характер.

Очевидно, что количество трасс Т{(Ха, Хь) удовлетворяет нера

венству

|{Г,(Хв,Х ь)}| <Н(Ха,Хь)\,

где Н(Ха, Хь) — расстояние по Хеммингу между точками Х а, Хь.

Интервал [0, 15] рассматривае

мой функции содержит шесть

трасс:

Г^О, 15) <4 и(0) < и(4) <

< и(6) < и(7) < и(15),

Щ 0, 15) <4 и(0) < и(4) <

< v(6) < v(14) < v(15),

Т3(0, 15) О и(0) < и(8) <

< и(9) < и(11) < и(15),

Т4(0, 15) <4 и(0) < и(8) <

< и(9) < и(13) < и(15),

Г5(0, 15) <4 t7(0) < 17(8) <

< и(10) < и(11) < и(15),

Гв(0, 15) <4 и(0) < 17(8) <

< и(10) < и(14) < и(15),

из 24 цепей, соединяющих точки

0 и 15.

Максимальная длина трассы в пространстве размерности п

равна диаметру соответствующего гиперкуба, т. е. числу п.

Минимальная длина трассы в пространстве той же размерно

сти равна 2.

В рассматриваемом случае трассами длины 2 являются:

Т(0, 5) <4 и(0) < 17(4) < «(5);

W ' 5

Рис. 2.18

148

Гл. 2. Математическая логика

770 Ш ' U(0) < U(4) < U(12)’

1 ’ ; % «(0) < «(8) < «(12);

Т(4 13) S U(4) < U(5) U(13)’

' ’ ** «(4) < «(12) < и(13)

Т(8, 13) <-> «(8) < «(12) < и(13)

Т(8, 14) <-> и(8) < «(12) < «(14)

m is) ' и(5) < и(7) < и(15)’

^ } % «(5) < «(13) < «(15);

ТП 9 i i\ ^ U(12> < U(13> < U(15)’

** «(12) < «(14) < «(15).

Распределение трасс в булевом пространстве определяет качество

переходного процесса: чем больше трасс, тем больше возможность

порождения ложной информации (количественная оценка будет

рассмотрена в гл. 5); чем больше расстояние по Хеммингу между

концами трассы, тем больше длительность сигнала ложной ин

формации.

Введем функцию R(xai, xaj, . . xak) риска сбоя (т. е. ложной

информации):

' 1, если возможна ложная

п/ \ _ информация хотя бы на одной

Л(Ха1, Ха2, . • ., Хак) — ИЗ if! цепей Ca(*6i 1*63, M*6fc)i

„ 0 в противном случае,

где xai, xaj, ..., Xak — переменные интервала [Ха , Хр], изменяю

щие свое значение на противоположное:

ХакХ/з=Ху, xai $ Ху, * = 1,2,..., Л.

Условие порождения трассы определяет формула

R(xaj , Xaj )

) =

dkf

@(Х(ц t Xa2, . . ., Xak)

^3ca (ij1, i j j , ..., sjfc) £ ^c,'(i,'j, ®i2, ..., xik)J

s ( df „ d2f

.............

........

...

• • - e‘ >- i « K ) fe W ^ T )

d*f

&(Xbii Xfe, Xf,3)

-------

V - l l

---------

-) = l} Y (2.24)

@\xbx i Xb3 ) • • m Xf>k_l )/ J J

§2.10. Теория трасс 149

где:

dkf/d(xaj, ха2, . • хак) — производная ох булевой функции

/ по переменным ха1, х„2, .. x0fc, единичное значение которой

указывает на изменение значения функции / при одновременном

изменении значений переменных ха1, ха2, • • хак;

perm (01, яг, ..., ah) — результат перестановки (permutation)

индексов ai, а2, ..., а*;

переменные xbl ,хь2,..., хьк попарно не равны друг другу (<8>(хЬ1,

хь2, • ■ хьк)) и являются элементами множества переменных

{*®1> *аг> • • •) *a*}•

Вычислим функцию риска сбоя при переключении каналов xi,

Xi для ИС (см. рис. 2.17, а):

д2/ df d2f df

- е п t ф

d(x i, х 2) d x i dx\dx2 dx г’

f ( x i, X2, X3, X4) = X!X2X4 V ЩХ3Х4 V ЦХ2Х3Х4 V X1X2X3X4;

= f ( x 1 = 1) ф f ( x 1 = 0),

/(x i = 1) = *2*3*4 V X2*3*4i /(*1 = 0) = 12*4 V X3X4 .

После тождественных преобразований получаем

Q / О/

— = х 2х 4 V х2х4 V х 3, — = /(х 2 = 1) ф /(х 2 = 0),

Имеем

З2/

/( * 2 = 1) = * 1 *3*4 V Х1 Х3Х4 V Х1 Х3Х4 ,

/(Х2 = 0) ='*1*4 V Х1Х3Х4.

d f _ _ _ _

■5— = Х1 Х4 V Х3 Х4 V Х1 Х3Х4 ,

ОХ 2

\d x 2 J

(Х3Х4 V Х3Х4) ф х4 = х3.

5xi d x2

Отсюда

02/

___

______

—

--------

т = (х2*4 V х2х4 V х3) ф х3 ф (xix4 V Х3 Х4 V Х1 Х3Х4).

о(х1, х2)

В результате тождественных преобразований получаем

d2f

d(x 1, х2)

9(хь х2)

= V(1, 2, 3, 5, 9, 13, 14, 15),

= V(0, 4, 6, 7, 8, 10, 11, 12).

150

Гл. 2. Математическая логика

Согласно формуле (2.24)

d2f

d(xlt х2) dxi

ft f

k - — = X1X2X3X4 V XlX2X3X4 V XiX2X3X4V

V X\X2X3X4 V xix2x3i4 V xix2®3*4) (2.25)

d2f c df

k -г— = xix2x3x4 V * 1X2^ 32:4 V X1X2X3X4V

d(xi, x2) dx2

V XXX2X3X4 V X1X2X3X4 V XiX2^3X4.

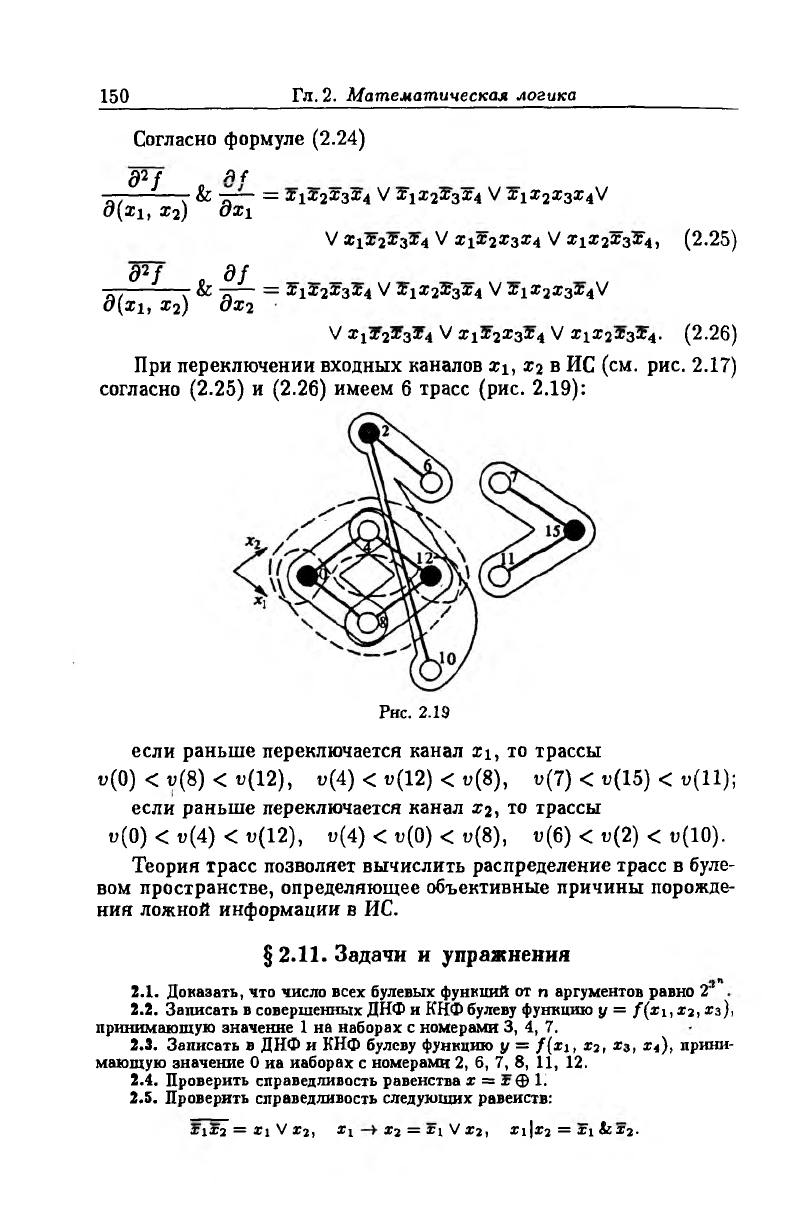
При переключении входных каналов xi, х2 в ИС (см. рис. 2.17)

согласно (2.25) и (2.26) имеем 6 трасс (рис. 2.19):

(2.26)

Рнс. 2.19

если раньше переключается канал xi, то трассы

и(0) < и(8) < и(12), и(4) < и(12) < и(8), v(7) < v(15) < v(ll);

если раньше переключается канал х2, то трассы

и(0) < и(4) < и(12), и(4) < и(0) < и(8), и(6) < и(2) < и(10).

Теория трасс позволяет вычислить распределение трасс в буле

вом пространстве, определяющее объективные причины порожде

ния ложной информации в ИС.

§2.11. Задачи и упражнения

2.1. Доказать, что число всех булевых функций от п аргументов равно 2

2.2. Записать в совершенных ДНФ и КНФ булеву функцию у = f(xi, хг, хз),

принимающую значение 1 на наборах с номерами 3, 4, 7.

2.3. Записать в ДНФ и КНФ булеву функцию у = f(x\, хг, хз, х*), прини

мающую значение 0 иа наборах с номерами 2, 6, 7, 8, 11, 12.

2.4. Проверить справедливость равенства х = х ф 1.

2.5. Проверить справедливость следующих равенств:

X l X 2 = X l V X 2 , X! Хг = Xl V Х2, Xl |Х2 = Xl & Х2.