Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§2.11. Задачи и упражнения

151

2.6. Показать, что число булевых функций, существенно зависящих от п

аргументов, определяется рекуррентным соотношением

1=0

где А, — число булевых функций, зависящих от i аргументов.

2.7. Булева функция /, зависящая от трех аргументов, называется мажори

тарной, если имеет место равенство / = xixj V Х1Х3 V Х2Х3. Будем обозначать

Sty операцию знаком # и записывать х1#хг#хз.

Доказать, что имеют место следующие соотношения:

1) x i # x i# x 2 = x i ; 2) X i# x i# x 2 = хг; 3) х 1 # х г # х з = 5 i #X 2 # X 3.

2.8. Найти минимальную ДНФ функции у = f(xlt 12, хз, 14), принимаю

щей значение 1 на наборах 0, 1, 2, 5, 6, 7, 8, 12, 13.

2.9. Найти минимальную ДНФ функции у = /(х 1, Х2, хз, ц , Х5), при-

нимающей значение 1 иа наборах с номерами от 0 до 7, от 11 до 21 и от 26

до 31.

2.10. Функция у = fix 1, Х2, хз) равна 1 на наборах 1, 3, 4 и не определена

ва наборе с номером 5. Найти ее минимальную ДНФ.

2.11. Разработать тест распознавания противоречивого задания неопреде

ленной булевой функции fixi, хг, ..., х„) (функция задана противоречиво,

если (ЗЛГ)(/(ЛГ) = 0, 1)).

2.12. Найти минимальную ДНФ булевой функции

,, , / 1 на 01- 0 -, 001- 0, —010—,

ДХ1, х2, ..., хь) - иа ц о - 1, 000- 1, 1001- .

2.13. Определить скобочную форму булевой функции

,, \_/1 на - 0- 100,100 - 0 1 ,- 0 1

-------

/(x i, х2, . . хв) — ^ о на 110—О-, 011

----

0, 00- 1- 1.

2.14. Найти мощность единичной области неопределенной булевой функции

/(х 1, хз, ..., Х5) после ее доопределения:

,, \ Г 1 на 001- 1, 01- 01, -4011-,

/(x i. х2, ..., х5) - иа 0001—, 100—1, 11—011.

2.15. Проверить линейность булевой функции

/(* 1, xi, x3)|i = V(0, 1, 5, 6).

2.1С. Установить, является ли самодвойственной функция эквивалентности.

2.17. Проверить монотонность конъюнкции от п аргументов.

2.18. Привести пример монотонной функции, которая одновременно была бы

линейной.

2.19. Привести пример самодвойственной функции, которая одновременно

была бы линейной.

2.20. Привести пример линейной и монотонной функций.

2.21. Убедиться, что функции Шеффера и Бебба ие являются ни линейными,

Ни монотонными, ни самодвойственными.

2.22. Установить, образует ли булева функция/(x i, хг, хз, X4)|i = V(0,3,7,

И, 13) базис в Рг-

2.23. Верно ли утверждение: если булева функция существенно зависит

более чем от одного аргумента и оиа монотонна, то она несамодвойственна?

2.24. Верно ли утверждение: если булева функция существенно зависит

более чем от одного аргумента и оиа линейна, то она немонотонна?

2.25. Найти все булевы функции, удовлетворяющие системе уравнений

V>(x) -¥= <fi(x)<fi(x) = 0.

2.26. Доказать следующую теорему: при суперпозиции линейных функций

(подстановке функций в функцию вместо ее аргументов) получаются линейные

Функции.

152

Гл. 2. Математическая логика

2.27. Доказать теорему: при суперпозиции самодвойственных функций

вновь получаются самодвойственные функции.

2.28. Доказать теорему: при суперпозиции монотонных функций вновь по

лучаются монотонные функции.

2.29. Функция называется сохраняющей константу г (г = 0, 1), если на

наборе аргументов вида (г, г, ..., г) она принимает значение г. Доказать, что

суперпозиция функций, сохраняющих константу г, вновь является функцией,

сохраняющей эту константу.

2.30. Если функции <pi и ipi самодвойственны, то самодвойственны ли функ

ции Ifil V Ifi3, Ifil¥>2? _

2.31. Если функции <pi и у>2 линейны, то линейны ли ifii Vtf3, Vi и V>i -* V>2?

2.32. Булева функция называется симметричной, если она не изменяется

при любом переименовании аргументов. Фундаментальной симметричной бу

левой функцией индекса т называется такая симметричная булева функция, у

которой все конъюнкции, входящие в совершенную ДНФ этой функции, имеют

ровно т букв без отрицания.

Доказать следующую теорему: любая симметричная булева функция есть

дизъюнкция фундаментальных булевых функций, индексы которых однозначно

определяются представляемой симметричной функцией.

2.33. Определить число самодвойственных функций, зависящих от п аргу

ментов.

2.34. Доказать полноту системы булевой функции, состоящей из дизъюнк

ции, константы

и эквивалентности. Образует ли эта система базнс?

2.35. Образует ли базис система булевых функций, состоящая из имплика

ции и константы О?

2.36. Установить, является ли полной система, состоящая из дизъюнкции,

импликации и конъюнкции.

2.37. Образуют ли полную систему функция i\Xi VХ1Х3 Vхзхз и отрицание?

2.38. Доказать, что если некоторая булева функция не сохраняет константы

и несамодвойствениа, то она немонотонна и нелинейна.

2.39. Сравнить связности мографов, определяющих конъюнкцию и дизъ

юнкцию в 3-значной логике до и после минимизации.

2.40. Выяснить, возможна лн реализация любой булевой функции на эле

ментах УСЭППА (универсальной системы промышленной пневмо-автоматики),

являющихся пневмореле, описываемым функцией а(Ь V с) V bed.

2.41. Синтезировать логическую схему, реализующую булеву функцию

/(* 1, *2, хз, х\, xs, *e)|i = v(0, 1, 2, 5, 7, 11, 13, 15, 19, 20, 32, 57, 61, 62)

в базисе Вебба.

2.42. Синтезировать логическую схему, реализующую булеву функцию

/(* 1, х2, ..., r*)|i = V(0, 3, 5, 8, 10, 12, 14, 15, 17, 25, 27, 31)

в базисе {-*, 0}.

2.43. Определить сложность одноразрядного сумматора в базисе Шеффера.

2.44. Показать, что

Э/(х 1, xj, ..., ц, ..., Хп) df(x 1, хз, ..., xt, ..., х„)

дц дц

2.45. Установить, справедливо ли равенство

df(x 1, хз, ■■., хп) df(x 1, хз, ..., х„)

Эх, Эх;

2.46. Синтезировать логическую схему, реализующую булеву функцию

f(x 1, Х2, хз, Х4, x5)|i = v(0, 3, 5, 8, 10, 12, 14, 15, 17, 25, 27, 31)

в базисе Вебба.

2.47. Определить сложность одноразрядного сумматора в базисе {-«, 1}.

§2.11. Задачи и упражнения 153

2.48. Синтезировать логическую схему, реализующую булеву функцию

/(* 1, х2, хз, *4, *e, *e)|i = v(0, 1, 2, 5, 7, 11, 13, 15, 19, 20, 32, 57, 61, 62)

в базисе {->, }.

2.49. Синтезировать логическую схему, реалиаующую булеву функцию

/(* ,, ха, хз, х4, *s)|i = V(0, 1, 2, 5, 6, 7, 11, 12, 15, 16, 18, 25, 30)

в базисе {ai V a2 V аз}-

2.50. Синтеаировать логическую схему, реализующую булеву функцию

/(х 1, х2

.......

xT)|i = V(0, 2, 4, 5, 6, 7, 11, 12, ..., 81, 101)

в базисе {—f, 0}.

2.51. Определить порядок исключения переменных при реализации булевой

.функции

/(x i, ха, хз, x«)|i = V(0, 1, 2, 4, 7, 8, 11, 15),

если имеется каталог реализации всех функций от двух переменных.

2.52. Установить, что больше: вес производной df/дх2 или вес производной

d f /дхз от булевой функции

/(х 1, Х2, хз, X4)|i = V(l, 3, 7, 8, 12, 14, 15).

2.53. Предложить алгоритм подсчета веса производной от булевой функции

С использованием двоичных матриц.

2.54. Установить, что выгоднее с точки зрения уменьшения аппаратурных

затрат в базисе импликации и константы 0: исключение по одной переменной

Или исключение по двум переменным.

2.55. Найти все остаточные функции при оптимальном порядке исключения

переменных булевой функции

/(х 1, Х2, хз, Х4)11 = V(0, 4, 6, 8, 10, 13, 14, 15).

2.56. Сколько входов имеет блок исключения к переменных?

2.57. Найти реализацию блока исключения одной переменной в базисе Вебба.

2.58. Какова сложность блока исключения одной переменной в базисе Шеф

фера?

2.59. Найти вес производной df /дц от булевой функции f(x\, х2, хз)|1 =

« V(0, 1, 5, 6, 7).

2.60. Показать, что

df(x 1, Х2, ..., Xi, ..., Хп) _ df(l 1, Хд, ..., Xi, ..., хп)

дх, дх,

2.61. Найти производную первого порядка для функции цепи переноса в

Яолном одноразрядном сумматоре.

2.62. Определить производную второго порядка от функции суммы в пол

ном одноразрядном сумматоре, определяющую условия переключения функции

суммы при переключении каналов, соответствующих слагаемым.

2.63. Доказать, что любая булева функция однозначно определяется значе

нием функции и всех производных в точке 00.. .0.

2.64. Спроектировать счетчик нечетности в коимпликативном базисе.

2.65. Спроектировать одноразрядный сумматор в нмпликагивном базисе.

2.66. Синтезировать схему, реализующую функцию, принимающую значе

ние 1 на тех наборах своих пяти аргументов, в которых есть не менее четырех

единиц. При синтезе использовать элементы эквивалентности, дизъюнкции и

отрицания.

2.67. Синтезировать дешифратор иа три входа и восемь выходов, используя

ввементы V, &,

2.68. Реализовать функцию импликации иа элементах, реализующих отри-

Дание и функцию у = Х1Х2 V Х1Х3 V Х2Х3.

2.69. Реализовать импликацию иа элементах, реализующих функцию Вебба.

154

Гл. 2. Математическая логика

2.70. Реализовать сумму по модулю 2 на элементах Шеффера.

2.71. Реализовать одноразрядную суммирующую схему на элементах

V' ~ „

2.72. Реализовать одноразрядную суммирующую схему с учетом совместной

минимизации функции суммы и переноса на элементах V, &,

2.73. Доказать, что полный дешифратор на п входов может быть построен

из двух полных дешифраторов н а т и п - т входов и 2" элементов типа И.

2.74. Реализовать иа мажоритарных элементах и элементах НЕ функцию

У = *1X2 V Х1Х2Х3.

2.75. Реализовать функцию у = xi -» (хг -¥ хз) иа элементах у = x i#

# х 2#хз и НЕ.

2.76. Реализовать на мажоритарных элементах и элементах НЕ схему про

верки кода на четность, т. е. схему, на выходе которой при четном числе единиц

на входе схемы возникает единичный сигнал. Число входов равно 3.

2.77. Доказать, что

т т . т ) = в « х )° т

dxi dxi dxi дх* dxi

2.78. Доказать, что

дх, дх i дц дц dxi

2.79. Разложить булеву функцию

/(х 1, Х2, хз, Х«) = XlXjXl VX2X3X4 VX1X2X3

в ряд, аналогичный ряду Тейлора, в точках 2, 11. Сравнить количество первич

ных термов в полученных разложениях.

2.80. Записать основные законы алгебры Буля при арифметической интер-

претапии следующих логических операций:

x k y = x-y, xV y = x-fy — Х'у, х = 1 —х,

где •, + ,

------

арифметические операции умножение, сложение и вычитание со

ответственно.

2.81. 1) Список термов исчисления: {/, +, =}.

Правила образования формул следующие: I — формула; если ip — формула,

то ifil — также формула; если (риф — формулы, то ip + <j>Hifi = <j> — также

формулы.

Заданы единственная аксиома 1 + 1 = 11 и два правила вывода: если <pi +

+ / = ifi2 — выводимая формула, то (fiil+1 = ifijl — также выводимая формула;

если V>i+V>2 = V>3 — выводимая формула, то ifii+<pil = <fisl — также выводимая

формула.

Доказать, что:

а) формула II + III = / / / / / выводима в данном исчислении;

б) формула 1 + 1 = 1 невыводима в данном исчислении.

Множество термов состоит из бесконечного числа букв и знаков V и -К

завила образования формул следующие: любая буква есть формула; если

а и 0 — формулы, то а\/0иа-*{3 — также формулы.

Система аксиом такова: AV А -¥ А-, А —У AV В\ А V В -¥ В V А; (А

- + 8 ) 4 ((С -4 А) (С В)).

Правила вывода таковы.

Правило подстановки: если а — выводимая формула и вместо любой пере

менной в этой формуле всюду произвести подстановку лообой формулы, то новая

формула также выводимая.

Правило заключения, если а -¥ (3 я а — выводимые формулы, то /3 также

выводимая формула.

§ 2.11. Задачи и упражнения

155

В данном исчислении (исчислении Гильберта) доказать, что:

1) выводима формула А -¥ А;

2) если А -» (В -¥ С), Ап В выводимы, то выводима и формула С.

2.82. Используя результаты предыдущей задачи, доказать, что в исчислении

Гильберта имеет место следующее утверждение: если « -» (/? -» 7 ) выводимо,

$о /3 -¥ (а у) — также выводимая формула.

2.83. Введено следующее исчисление (исчисление Лукасевича): множество

Термов состоит из бесконечного числа букв и знаков —,

Правила образования формул: все буквы есть суть формулы; если tp — фор

мула, то Тр — также формула; если и ф — формулы: то <р -» ф — также

формула.

Система аксиом следующая: (А -¥ В) -¥ ((В -4 С) -*• (А -¥ С)); (А —У

А) —^ А; А —^ (А —^ В).

Справедливы правило подстановки и правило заключения.

Доказать, что в исчислении Лукасевича выводима формула А -* А.

2.84. Исчисление задано следующим образом (исчисление

Новикова): мно

жество термов состоит из бесконечного числа букв и знаков V, Л,

Правила образования формул:

а) все буквы суть формулы;

б) если а — формула, то а — также формула;

в) если а и (3 — формулы, то а V/З, аЛ/3, а -» /3 — также формулы. Система

аксиом состоит из следующих одиннадцати аксиом:

1) А —f (В —^ А); 2) (А —> (В —> С)) —^ ((-^ —^ В) —> (А —¥ С?));

3) А Л В -* А; 4) А Л В В; 5) (А -* В) -* ((А -* С ) А -¥ (В Л С));

6) А —f А V В; 7) В —> А V В; 8) (А —> С) —> ((В —> С) —> (А V В) —> G);

9) (А -4 В) -4 (А -4 В); 10) А -» А; 11) А -4 А.

В качестве правила вывода используются правило подстановки и правило

«включения.

Доказать, что система аксиом является непротиворечивой.

2.85. Доказать, что аксиома 9) в исчислении Новикова является независимой

ко отношению ко всем остальным этого исчисления.

2.86. Пусть предикаты N(x), С(х), Р(х), П(х), Ч(х), Д(х, у) имеют со

ответственно смысл: х — натуральное число, х — целое число, х — простое

Число, х — положительное число, х — четное число, х делит у. Сформулировать

Смысл следующих формул узкого исчисления предикатов (и указать, какие из

№ являются тождественно истинными):

1) (Ух)(ЛГ(х) -4 С(*));

2 )(V x)(C (x)-»(x)V (x));

3) (Vx)(3y)(C(x) Л С(у) -4 Д(х, у));

4)(Эх)(Р(х)Л (х));

5) (Vx)(C(x) Л Я(х) -4 Щх)).

2.87. Описать множество истинности следующих двуместных предикатов,

определенных на множестве действительных чисел:

х2 - у2 = 0; (х > 0) Л (у < 0); (х > О) -4 (у < О).

2.88. На множестве М определены одноместные предикаты F(x) и G(x).

Каким условиям удовлетворяют области их истинности, если истинны:

1) (Vx)(F(x) -4 G(x)) Л (3x)(F(x) Л G(x));

2) (3x)(F(x) Л G(x)j Л (3x)(F(x)

-4

G(x))?

2.89. Доказать эквивалентность следующих формул:

a) 3(x)F(x) и V(x)F(x);

156

Гл. 2. Математическая логика

б) V(x)(F(x) -* Л) и 3(x)(F(x) -» Л);

в) У(х)(Л -» F(x)) и А -> V(x)F(x).

2.90. Доказать эквивалентность формул:

а) 3(х) (А Л F(x)) и А Л 3(x)F(x);

б) 3(x)(F(x) V G(x)) и 3(x)(F(x) -> Л);

в) Л V V(x)F(x) и V(x)(A V F(x)).

2.91. Установить, как можно построить теорию нормальных форм в исчи

слении предикатов.

§ 2.12. Комментарии

Математическая логика — это анализ методом рассуждений, при этом в

первую очередь исследуются формы рассуждений, а не их содержание. Форма-

лизапия рассуждений восходит к Аристотелю. Современный вид аристотелева

(формальная) логика приобрела в середине XIX века в работах профессора Ка

занского университета Платона Порецкого (1844 г.), Джорджа Буля и Августа де

Моргана (1847 г.). Математическую логику иногда называют логистикой (школа

Рассела). Б становление логики внесли большой вклад и другие ученые того вре

мени: Эрнст Шрёдер, Джузеппе Пеано, Джон Венн, Александр Макфарлейн.

Интенсивно математическая логика развивалась в 50-годы нашего столе

тня в связи с бурным развитием цифровой техники. В 1910 г. русский фнзик

П. Эренфест указал иа возможность применения логики высказываний для опи

сания переключательных цепей в телефонной связи. В 1938-1940 гг. почти

одновременно появились работы советского ученого В.И. Шестакова, американ

ского ученого Шеннона и японских ученых Нахашимы и Ханзавы о примене

нии математической логики в цифровой технике. В 1951 г. в СССР была при

нята в эксплуатацию первая в Европе вычислительная машина — МЭСМ (малая

электронная счетная машина), разработанная под руководством С.А. Лебедева.

Первая монография, посвященная использованию математической логики при

проектировании цифровой аппаратуры, была опубликована в СССР советским

ученым М.А. Гавриловым в 1950 г.

Для углубления знаний по математической логике рекомендуем [8, 11,

24, 30].

Природа говорит языком математики: бук

вы этого языка — круги, треугольники и

иные математические фигуры.

Г. Галилей

Глава 3

ТЕОРИЯ ГРАФОВ И МОГРАФОВ

§ 3.1. Взвешенный граф и его матричное задание

Выше понятие графа было определено как совокупность множе

ства вершин V и дуг Ui С V 2. Дуга и, соединенная с вершиной

V, называется инцидентной вершине и, а вершина и — коин-

цидентной дуге и. В дуге (и,, vj) вершины и,- и Vj называются

граничными, причем и,- — начало, Vj — конец дуги., Для учета

изолированных вершин, т. е. вершин, не коинцидентных ни одной

дуге, расширим понятие грэфа G до совокупности вида

G = (V,lh,U2), IhcV, U2 CV2,

Где унарное отношение U\ определяет изолированные вершины,

U2 — дуги.

При удалении дуг из графа G = (V, U\, U2) получаем частич

ный граф G' С G, G' = (V, Ui, Щ), Щ С U2, графа G; при уда

лении вершин и инцидентных им дуг получаем подграф G" =

ЙВ {V", £/", UH), V" С V, U" С Ui, Щ С U2, графа G; при даль

нейшем удалении дуг из подграфа G" графа G получаем частич

ный подграф G = (V, U\ , J72) графа G.

Две дуги, иа и up, называются смежными, если они инци-

деитны одной и той же вершине.

Две вершины, va и uj, называются смежными, если они сое

динены дугой.

Множество вершин, смежных с вершиной va, называются ее

окрестностью и обозначается 0(va) или Г(иа). Используя по

нятие окрестности, граф определяют как совокупность множества

вершин и множества их окрестностей: G = (V, Г).

Определим понятие взвешенного графа. Сопоставим каждой

вершине vi £ V (V = {и,/ j = 1,2,..., п}) графа G = (V, U\, U2)

вес Wi из множества весов W = {w,/ i = 1,2,...}. В результате

получим множество взвешенных вершин {(и,-, -ш,)/* = 1,2,..., п};

При этом не обязательно, чтобы все веса были различными.

Сопоставим каждому элементу множества £72 = {щ / * = 1, ■ • ■

..., тп} вес pi из множества весов Р = {р,/ г = 1, 2, ...}. В резуль

тате получим множество взвешенных дуг {(u,-, p i)/ * = 1,2,...

158

Гл. 3. Теория графов и мографов

..., тп}; при эхом не обязательно, чтобы все веса были различ

ными.

Множества взвешенных вершин и дуг определяют в совокуп

ности взвешенный граф G = ((F, W ), (U, Р)), V = V U U\, кото

рый, строго говоря, является уже не графом, а функцией, опреде

ленной на вершинах и дугах графа.

Для задания графов существует несколько классов матриц, ос

новные из которых — класс матриц инциденций и класс матриц

смежности. Рассмотрим эти классы матриц.

Класс матриц инциденций. Если граф G содержит п вершин

и т дуг, то матрица инциденций A(G) = [а„]тХп определяется

как

а,-

если вершина vj — начало дуги и<,

если вершина vj — конец дуги щ,

если вершина vj не коинцидентна дуге щ.

Иногда граф содержит петли, т. е. дуги вида (и,-, и,). В этом

случае некоторые элементы матрицы А одновременно равны и 1,

и —1, что приводит к неоднозначности элементов матрицы А.

Для задания графа с петлями “расщепим” матрицу А на две

матрицы, А+ и А~ (А+ — начальная, А~ — конечная матрица

инциденций):

{о

если верщина vj является началом дуги щ,

в противном случае;

= [%]

mXft)

где

■ и . 1.

если вершина Vj является концом дуги щ,

О в противном случае.

Если граф без петель, то

А+ — А~.

Матрицы

А+

А~

опи

сывают граф без учета весов вершин и дуг. Зададим веса вершин

графа G в виде столбцовой матрицы

W(G) =

а веса дуг — в виде диагональной матрицы порядка тп

0 0 . .. 0

P(G ) =

Р2

0 .

.. 0

0 0 .

• • Рт

Матрицы Л+, А , W , Р полностью описывают взвешенный граф.

§3.1. Взвешенный граф и его матричное задание

________

159

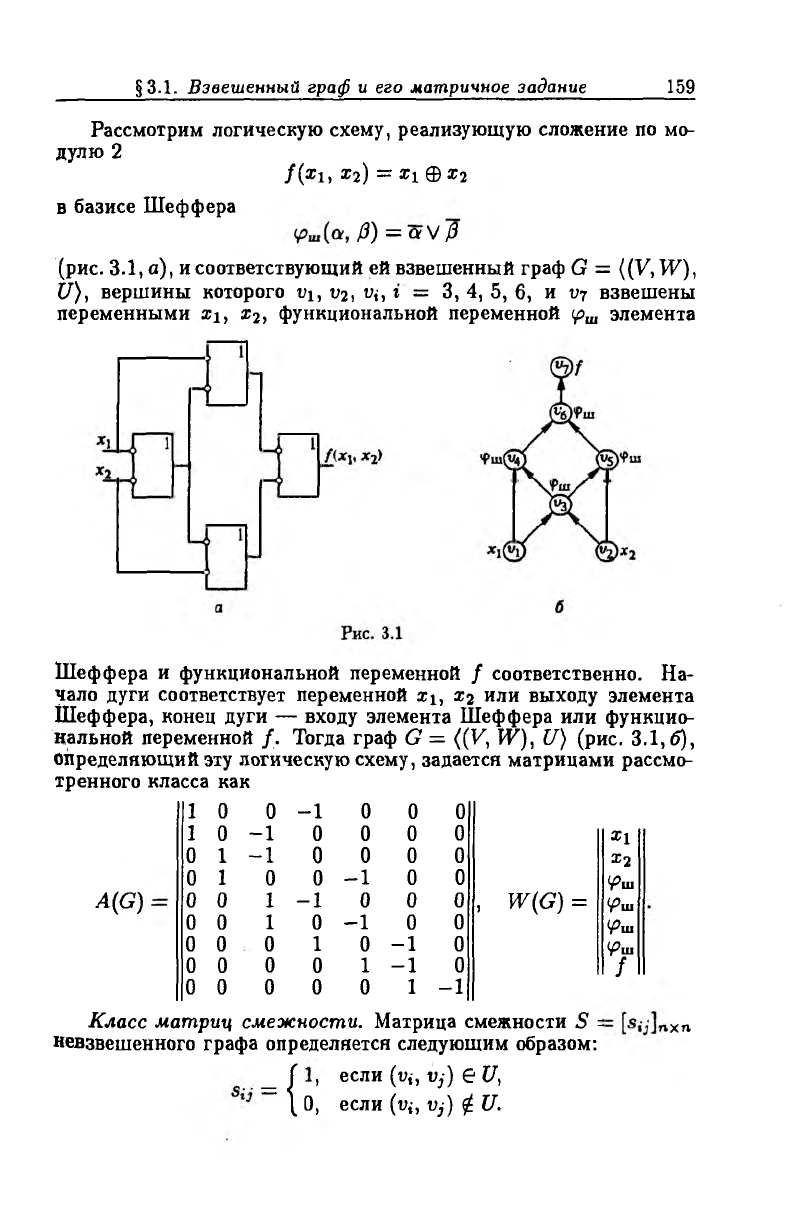
Рассмотрим логическую схему, реализующую сложение по мо

дулю 2

f(x 1, х2) = xi фх2

в базисе Шеффера

/3) = а V /3

(рис. 3.1, а), и соответствующий ей взвешенный граф G = ((V, W),

U), вершины которого t^, v2, щ, t = 3, 4, 5, 6, и vy взвешены

переменными х\, х2, функциональной переменной (рш элемента

Шеффера и функциональной переменной / соответственно. На

чало дуги соответствует переменной х\, х2 или выходу элемента

Шеффера, конец дуги — входу элемента Шеффера или функцио

нальной переменной /. Тогда граф G = ((V, W), U) (рис. 3.1,6),

определяющий эту логическую схему, задается матрицами рассмо

тренного класса как

A(G)

1 0

-1 0

0 0

-1

0 0 0

0 1 -1

0 0 0

0 0

-1

0 0

0 0 1 -1 0 0 0

0 0

-1

0 0 0

-1

0 0

1 -1 0

0 0 0 0 0

1 -1

, W(G) =

х2

<Рш

Класс матриц смежности. Матрица смежности S =

невзвешенного графа определяется следующим образом:

если (и,-, vj) € U,

если (и^, vj) ^ U.

ХП

= {о!

160

Гл. 3. Теория графов и мографов

Для взвешенного графа

_ j pij, если дуга (и^, и;) € U имеет вес р^,

S'3 \ 0, если (и^, vj) $ U.

Матрицы S, W, Р полностью описывают взвешенный граф.

Например, граф G (рис. 3.1, б) задается матрицами этого класса

как

1 1

0 0 0

1 0 1

0 0

1 0 0

<Рш

0 0 0 0 0 1 0

, W(G) = <Рш

0 0

0 0 1

<Рш

0 0

4>ш

0 0

При задании графа G (рис. 3.1,6) отсутствует матрица P(G),

так как дуги этого графа не взвешены.

Два графа, G = (V, U) и G1 = (V', U’), называются изоморф

ными, если существует такое взаимно однозначное соответствие

между вершинами множеств V = {t^} и V' = {и,-}, что вершины

иа, и;, соединены дугой (va, vb) в одном из графов в том и только

том случае, когда соответствующие им вершины и ', v'b соединены

дугой (v'a, v'b) в другом графе.

Матрицы рассмотренных классов задают графы с точностью

до изоморфизма.

Обозначим через (А+)т транспонированную матрицу инциден-

ций А+. Матрица смежности, начальная А+ и конечная А~ ма

трицы инциденций и диагональная матрица весов дуг связаны

следующим равенством:

S ~ (Л+)т • Р • (А- ). (3.1)

Степенью s(v) вершины v называется число дуг (ребер), ин

цидентных этой вершине.

Используя понятие мографа, можно задавать более эффективно

в смысле затраченного объема информации большие графы G,,

матрицы смежности которых слабо заполнены единицами. Графы

этого класса имеют большое практическое значение.

Будем задавать связанный неориентированный граф G = (V,

U) без петель моделью Ф = (М, Si, 5г, . . S„), в которой М = V\

слово, определяемое 5,, представляет собой окрестность 0(иа) еди

ничного радиуса вершины va £ V, содержащую г — 1 вершину

va. Для иллюстрации этого задания рассмотрим тот же граф G

(рис. 3.1,6), не учитывая ориентацию его ребер. Матрица инци

дентности <2(Ф) в этом случае представляет собой матрицу смеж-