Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§3.3. Цикломатика и коцикломатика

171

пространства единственным образом представим в виде линейной

комбинации векторов множества. Если пространство имеет базис

из п векторов, то оно называется п-мерным пространством.

Базис циклов графа G — это базис пространства циклов графа

G , состоящий из простых циклов.

Вектор R зависит от простых циклов R i, R2, ..., Rn, если он

представим в виде линейной комбинации векторов

Д =

а ь

0 0

0 0 0

1 1 1

Яз

0 1 1 1 1

1 1

1 1 1

0 0

1 1

0 1

0 0

1 1

1 0

1 1 1

1 1

0 0

Любой вектор цикла графа G может быть представлен в виде

линейной комбинации векторов базиса циклов. Рассмотрим, на

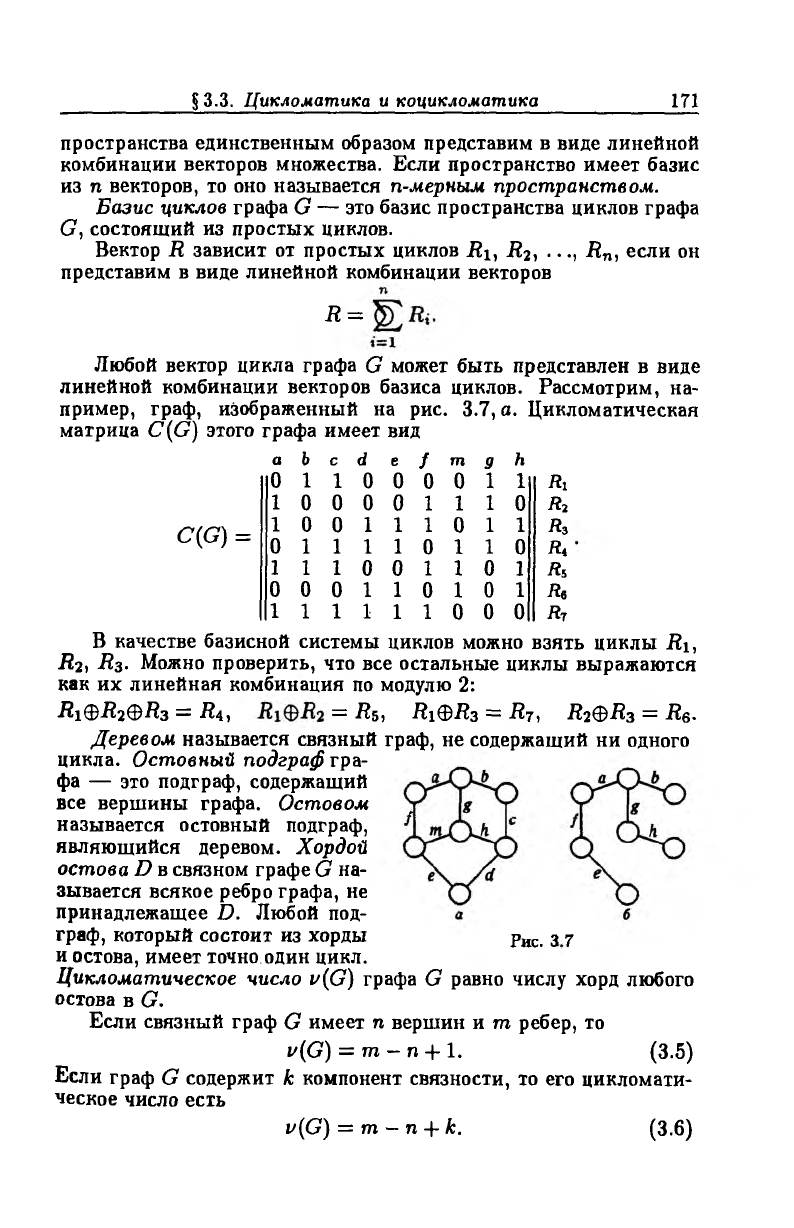
пример, граф, изображенный на рис. 3.7, а. Цикломатическая

матрица C(G) этого графа имеет вид

C(G) =

В качестве базисной системы циклов можно взять циклы Ri,

R 2, i?3- Можно проверить, что все остальные циклы выражаются

как их линейная комбинация по модулю 2:

Ri® R2®R3 = R i, = Rb, Ri®R3 = -^7) R2®R3 = Re-

Деревом называется связный граф, не содержащий ни одного

цикла. Остовный подграф гра

фа — это подграф, содержащий

все вершины графа. Остовом

называется остовный подграф,

являющийся деревом. Хордой

остова D в связном графе G на

зывается всякое ребро графа, не

принадлежащее D. Любой под

граф, КОТОрЫЙ СОСТОИТ ИЗ ХОрДЫ рис_ 3 7

и остова, имеет точно один цикл.

Цикломатическое число v(G) графа G равно числу хорд любого

остова в G.

Если связный граф G имеет п вершин и т ребер, то

i/(G) = т - п + 1. (3.5)

Если граф G содержит к компонент связности, то его цикломати

ческое число есть

v(G) = т — п + к. (3.6)

172

Гл.З. Теория графов ц мографов

Цикломатическое число несвязного графа может быть опреде

лено как сумма цикломатических чисел его компонент связности:

- ( о = £ ■ кед- (з-7)

i=l

Цикломатическое число определяет меру связности графа. От

метим, что свойства циклов графа и его разрезов похожи. Лесом

называется граф, не содержащий циклов. Иными словами, если

граф состоит из нескольких компонент связности, каждая из ко

торых является деревом, то данный граф является лесом. Если

лес G имеет п вершин и к компонент связности, то он содержит

п — к ребер.

Остовным лесом называется граф, каждая компонента кото

рого является остовным деревом.

Коциклический ранг x(G) (ранг разреза) — это число ребер

в его остовном лесе:

X(G) = п — к.

Количество базисных циклов в графе G определяется цикло-

матическим числом (циклическим рангом) графа v{G).

Теорема 3.11 (Эйлер). Число базисных циклов графа пос

тоянно и равно его цикломатическому числу.

Базисной системой циклов для данного остовного леса D гра

фа G называется множество всех циклов графа G, каждый из ко

торых содержит только одну хорду D . Эта система образует базис

пространства циклов. В рассматриваемом примере циклы R i, R2,

R3 являются базисом

c m d a b e f 9 h

C6(G) =

Полученная матрица является базисной цикломатической ма

трицей относительно остова D.

Выполняя 2" — v - 1 раз операцию сложения по модулю 2 над

базисными циклами, получаем все множество циклов этого про

странства.

Часто матрицу инциденций А и цикломатическую матрицу С

называют первой матрицей инциденций и второй матрицей ин

циденций соответственно.

Теорема 3.12. Вторая и первая матрица инциденций ли

нейного графа G связаны операцией матричного умножения:

C(G) х A(G) = 0(mod 2).

0 1

0 0 1

0 0

Хорды Остов D

§ 3.3. Цикломатика и коцикломатика

173

Доказательство теоремы основано на том факте, что если вер

шина Vj входит в t-й цикл Ci, то точно два ребра, Uki и и^, ин

цидентные этой вершине, включены в г-й цикл.

Запишем базисную систему разрезов для графа G и остовного

дерева D, изображенного на рис. 3.7, б:

{а, тп, </}, {Ь, с}, {е, d}, {jf, тп, с, d}, {d, h, с}, {/, тп, d}.

Эта система получена следующим образом. Удаляется ребро остова

D. Множество вершин при этом распадается на два непересекаю-

щихся подмножества, Vi и Множество всех ребер в G, каждое

из которых соединяет вершину из V\ с вершиной из V2, является

разрезом графа G. Множество всех разрезов для каждого ребра

остова D является базисной системой разрезов для данного осто

ва D.

Базисная система разрезов образует базис в пространстве раз

резов, или пространстве коциклов. Эта система может быть за

писана в виде соответствующей базисной матрицы разрезов, или

базисной коцикломатической матрицы:

tfe(G) =

Выполняя 2х — х ~ 1 Раз операцию сложения по модулю 2 над

коциклами, порождаем все множество коциклов (разрезов) графа.

Задавая в графе свойства циклов, можно определить класс гра

фов. Рассмотрим, например, двудольные графы. Двудольным гра

фом G(V\ , V2) называется граф, множество вершин которого раз

бивается на два непересекающихся подмножества, V\ и У2) так, что

каждое ребро в G соединяет две вершины из разных подмножеств.

Для того чтобы убедиться в том, что граф является двудольным,

достаточно проверить его циклы.

Теорема 3.13. Граф является двудольным тогда и только

тогда, когда все его циклы имеют четную длину (четны).

Доказательство. Пусть G — двудольный граф. Тогда мно

жество его вершин распадается на подмножества Vi и V2. Рассмо

трим любую вершину из V\. Для того чтобы получить цикл, про

ходящий через эту вершину, надо пройти по одному из ребер из

К в У2 и по другому из V2 в Vi по к раз. Таким образом, любой

цикл в G имеет 2к ребер, т. е. является четным.

abeghfmcd

1 0

0 0 0

0 1

0 0

0 0 0

0 0

0 1 1

0 0 0 0 0 1

0 1

Остов D Хорды

174

Гл. 3. Теория графов и мографов

Пусть теперь все простые циклы четные; докажем обратное

утверждение, что G — двудольный граф. Предположим, что G —

связный граф. Для любой вершины у,- 6 G обозначим через Vj

множество вершин, состоящее из и всех вершин, находящихся

на расстоянии четной длины от и,-; через Vi обозначим множество

остальных вершин, находящихся на расстоянии нечетной длины

от Vi. Пусть теперь имеются две вершины, Vj, Vk € V2, которые

соединены ребром. Поскольку между и,- и Vj, а также между v, и

vjt — четное число ребер, то цикл, проходящий через ребро (vj, Vk)

и вершину Vi, нечетный, но это противоречит условию, согласно

которому все циклы четные. Следовательно, вершины V2 не соеди

нены между собой. Аналогичное доказательство можно провести,

если G имеет несколько компонент связности.

В двудольном графе не обязательно каждая вершина из Vi

соединена с каждой вершиной из V2, но если это так, то граф

называется полным двудольным графом и обозначается К т,„, где

т — число вершин Vj, а га — число вершин V2. Граф К т<п имеет

т + п вершин и тп ребер. Полный двудольный граф Кit„ назы

вается звездным графом (звездой) и является деревом. Заметим,

что любое дерево является двудольным графом. Часто двудольный

граф называют графом Кёнига.

§ 3.4. Дифференцирование графов и мографов

Понятие производной в математическом анализе характеризует

степень изменения функции при малом изменении ее аргумента;

в основу понятия производной положено понятие предела. В дис

кретной математике отсутствует понятие предела, поэтому невоз

можно механически перенести понятие производной из непрерыв

ной математики в дискретную. Для решения оптимизационных

задач дискретной математики введем понятие производной, осно

ванное на использовании понятия частоты букв в словах некоторой

модели Ф.

Перед формальным определением производной рассмотрим сле

дующий пример. Пусть задан граф G (рис. 3.8, а), и нас интере

сует частота участия ребер в образовании остовов графа G. Граф G

содержит 8 остовов (рис. 3.8, о), и искомую частоту можно харак

теризовать, например, числом вхождений каждого из ребер в эти

остовы. Например, ребро а участвует 5 раз в образовании осто

вов, ребро с — 4 раза и т. д. Частота ребер будет характери

зоваться более полно, если наряду с указанными выше числами

вычислять числа, каждое из которых равно количеству остовов, в

которых содержатся два зафиксированных ребра. Например, реб

ра а и 6 содержатся в двух остовах. Еще более точно искомая

частота пары ребер pi и Pj определяется отношением числа осто

вов, которые содержат ребро р,- или pj, но не содержат их одновре

§ 3.4. Дифференцирование графов и мографов___________175

количества остовов графа, в

менно, к числу остовов, содержащих как ребро р,-, так и ребро ру.

(,fi ~ 2fij + fj) /fiji где fi, fj, fij

которые вошли ребра pi,

pj, pi и pj соответст

венно.

Это отношение пока

зывает степень неравно

мерности участия пар ре

бер в образовании остовов

графа.

Условимся в дальней

шем исследуемый про

цесс называть событием

S , происходящим при вы

полнении определенных

условий. В рассматривае

мом примере событием

S является образование

множеством ребер остова

графа G, а условием —

вхождение ребер графа в

данное множество. Собы

тие S может быть задано соответствующим предикатом P(S).

В рассматриваемом примере предметной областью является

множество ребер {а, Ь, с, d, е}. Мощность сигнатуры остова рав

на 3 (|У| — 1 = 4 — 1 = 3); следовательно, местность предиката

Р(5) также равна 3: Рз(£). Таблица, определяющая этот пре

дикат Р3(5), имеет 10 строк (по числу сочетаний из 5 по 3) и 6

столбцов (мощность предметной области):

Л?

Рис. 3.8

ь с d

Л (5)

1 1

0 1

1 1 1

0 1 1 0

1 1

0 1 1 1 0 1

0 0

0 1 0

1 1

0 1

1 0 1

1 0 0

1 1

1 0 1

1 1 0

Каждое событие определяет некоторую двумерную двоичную

матрицу Q = [jijjmxn, каждому столбцу которой взаимно одно

значно соответствует условие, входящее в событие, строке — сово

купность условий, при которых событие имеет место (при которых

176

Гл.З. Теория графов и мографов

P3(S) = 1), и

1, если j-e условие входит в г-ю совокупность

условий, при которых событие истинно,

О в противном случае.

Другими словами, каждое событие определяет модель, матри

цей инцидентности которой является матрица Q, т. е. условия,

входящие в событие, являются буквами модели, совокупности ус

ловий, при которых событие истинно, — словами модели.

Интенсивность участия условий (букв) в событиях (словах) бу

дем характеризовать с помощью частот их вхождения. Для этого

введем частотную матрицу отношений F = [/.'jjnxni характеризую

щую модель Ф, матрица инцидентности которой есть ф(Ф) =

= [<7ij]m X n -

Частотной матрицей отношений F = [/.j]nxn называется

матрица, каждой строке (столбцу) которой взаимно однозначно со

ответствует буква, и элемент Д, равен числу слов, в которые входят

буквы г и j , если i ф j, в противном случае (г = j) — числу слов, в

которые входит буква г. При этом если г = j, то /, — собственная

частота буквы, если же г ф j, то — взаимная частота букв

г и j.

Из определения частотной матрицы отношений F = [/.'у]пхп

следует, что она сама симметрична относительно главной диаго

нали, т. е. fij = fji, и что собственная частота любой буквы

не меньше взаимной частоты этой буквы с любой другой буквой:

fi > fir

Можно показать, что частотная матрица отношений F, харак

теризующая модель, матрица инцидентности которой Q удовле

творяет соотношению

QT х Q = F, (3.8)

где QT — транспонированная матрица Q (т — знак транспониро

вания матрицы).

Определим степень участия компонент графа G в наперед за

данном событии 5 в графе G , другими словами, степень неод

нородности компонент графа относительно заданного события.

Будем характеризовать эту неоднородность производной

dG/dS

графа G по событию S.

Производной dG/dS графа G по событию S называется не

ориентированный взвешенный граф (V, (U, Р)), носитель кото

рого совпадает с носителем модели, определяемой этим событием,

и пара вершин (и,’, vj) взвешена отношением частоты (/,- - /,_,) +

4- (fi — fij) их несовместного участия к частоте совместного

участия в событии S:

д с , ч f i - 2 fij + fj

§ 3.4. Дифференцирование графов и мографов

177

причем:

(ui) vj) $ U, если (dG/dS)(vi, Vj) = с»;

(Vi, vj) € U, если (dG/dS)(vi, Vj) — конечная величина, отлич

ная от нуля;

Vi = Vj, если (dG/dS)(vi,Vj) = 0.

Значение выражения (3.9) называется значением производной

на ребре (v,-, Vj).

Проиллюстрируем понятие производной от графа по событию

на двух примерах.

Пример 3.3. Пусть заданы граф G (см. рис. 3.8,а), и событие 5 — обра-

аование ребрами остова графа G. Найдем производную от графа G по событию

S, которая будет характеризовать интенсивность участия ребер в образовании

остовов графа G.

Заданное событие определяет модель, матрица инцидентности которой имеет

следующий вид:

Q =

В этой матрице каждому столбцу взаимно однозначно соответствует ребро

|графа G (условие, входящее в событие), строке — совокупность ребер, образую

щих остов графа (совокупность условий, при которых заданное событие имеет

Место) (см. рис. 3.8,6). Частотная матрица отношений F, соответствующая ма

трице Q, есть

d е

1 1 1

1 0

1 0 0 1

1 1

0 1 1

0 1 1 1

0 1 1

0 1 0

F = Q*xQ

Элементы этой матрицы определяют dG/dS, представляющую собой граф, но

ситель которого — {а, Ь, с, d, е}, и две вершины этого графа смежны, если зна

чение производной на дуге, образуемой этими вершинами, отлично от нуля и

бесконечности. Вычисляя значения производной dG/dS на ребрах графа:

2 f 0b + fb 5-2-2 + 5

fab

' 'ifас "I" fc

dG I _ 1Л _ /«

9S{[a' b)-~

d G , 4 fa

-------

V.-------------

9GI:, 4 fd — 2fdc + fc 5

_ Ке) =

-------

---

-------

= _

5-2-24-4

2-24-5

= 3,

= 2,5,

= 3,

Получаем граф dG/dS (см. рис. 3.8,в).

Пример 3.4. Рассмотрим граф G (рис. 3.9,а), иа котором задано событие

"S — образование ребрами базисного цикла относительно остова G1 (рис. 3.9,5)

Графа G. Вычислим производную от графа G по событию 5.

178

Гл. 3. Теория графов и мографов

Цикломатическое число 1/(G) графа G равно 3:

u(G) = т — п + к = 7 — 5 + 1=3.

Следовательно, граф содержит 3 базисных цикла. Событие S определяет модель

вида

а Ь с d е д h

п_ 111 1 1 1 1 О О

4 - 0 0 1 1 1 1 о

||0 0 1 1 О 0 1

Этой модели соответствует частотная матрица отношений

F = Qr xQ =

Вычисляя значение производной, получаем граф dG/dS (рис. 3.9, в). Аиали-

с d е

1 1

0 0

1 1 1

1 0 0

1 1

3 2 1 1

3 2

2 2 2 1

0 е

0 0 1

0 1 1

0 1 h

Рис. 3.9

зируя граф dG/dS, замечаем, например, что ребра e n d (или ребра а и Ь)

одинаково интенсивно участвуют в заданном событии.

Таким образом, для определения производной от графа G по

событию S необходимо:

а) построить модель, определяемую заданным событием;

б) найти частотную матрицу отношений, соответствующую

этой модели;

в) вычисляя по частотной матрице отношений значения произ

водной на ребрах графа dG/dS, построить искомый граф dG/dS,

характеризующий интенсивность участия элементов графа G в за

данном событии S.

Производной dkG/dSk к -го порядка по событию S называ

ется производная от производной (к — 1)-го порядка по тому же

событию S:

dkG д f d ^ 'G '

dSk dS \d S k■

?)•

Смешанной производной по событиям Sa и Sj называется

производная по событию Sa от производной по событию S(,:

d2G д ( dG\

§ 3.4. Дифференцирование графов и мографов

179

Аналогично определяются смешанные производные от графа G

по событиям Si, S2, ..., Sn.

Введенное понятие производной от графа G по событию S дает

возможность находить производную и от модели Ф(<5) (от мографа

<j (m )(Q)). В случае определения производной от модели, если со

бытие S не оговорено, в качестве S будем считать “образование

буквами слова”.

Значение производной от модели (от мографа G^M\Q )) на паре

(г, j) есть

d G W

(*> i)

fi ~ 2 fij + fj

где частоты /,-, fij и fj определяются по частотной матрице отно

шений F = [/,_,] (F = Q T X Q). На мографе G(M) частоты /,-, fij

и fj равны соответственно числу весов вершины и,-, числу общих

весов вершин и,’, Vj и числу весов вершины Vj.

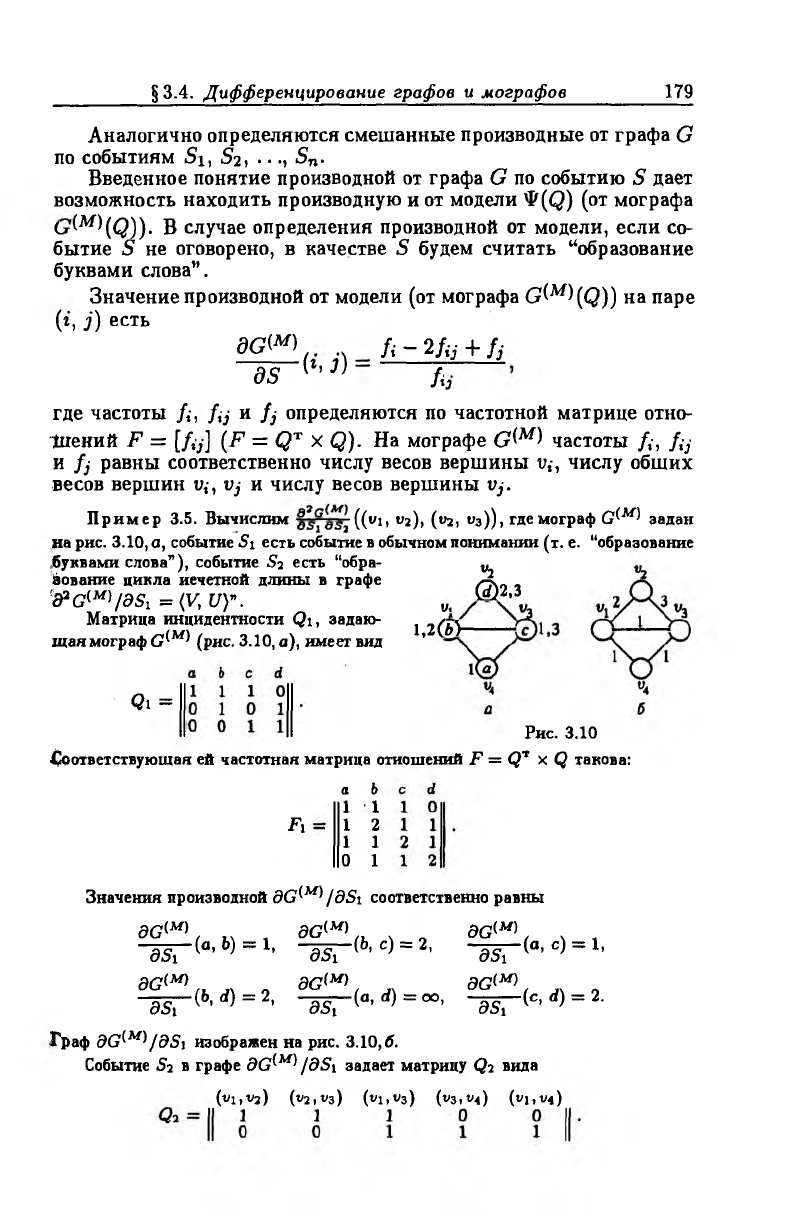
Пример 3.5. Вычислим ((fi, U2), («2, «з)), гдемограф G ^ задан

на рис. 3.10, а, событие 5i есть событие в обычном понимании (т. е. “образование

.буквами слова”), событие S2 есть “обра- ^

(2)2,3

1,2 (Ь)

кование цикла нечетной длины в графе

*&G(M)ldSi = (V, 17)”.

Матрица инцидентности Qi, задаю

щая мограф G*M' (рис. 3.10, а), имеет вид

Q1 =

Рис. 3.10

Соответствующая ей частотная матрица отношений F = Qv х Q такова:

а Ь

1 1

1 2

1 1

О 1

Значения производной 8G^M^ /dSi соответственно равны

dG(M) , dG(M> ч dG(M)

dSi

dG(M)

~dST

(a, b) = 1,

(b, d) = 2,

dSi

dGiM>

dSt

(b, c) = 2,

(a, d) = 00,

dSi

3G(M)

~dST'

(a, c) = 1,

(c, d) = 2.

Граф dG^M^/dSi изображен на рис. 3.10,5.

Событие S2 в графе 8G^M^ /dS\ задает матрицу Qi вида

(ui,V2) (ь’г . v3) (fi, V3) (V3,V4) (fi, V4)

180

Гл.З. Теория графов и мографов

Согласно алгоритму нахождения производной от графа находим

(vi,V

) («

,«з)

("i ,«s)

(V3,V4) (V1.V4)

1 1

f2 =

1 1

0 0

((ki, vj), (v3,

**)) =

2.1

_ 0

dSi dSi

Мы рассмотрели равномерность участия пар элементов в со

бытии 5. Аналогично можно рассмотреть равномерность участия

троек, четверок и т. д., n-к элементов в событии 5. Для вывода

формулы производной на 3, 4, . . п элементах обобщим понятие

частотной матрицы отношений. Введем понятие частотной гипер

матрицы отношений.

Рассмотрим модель Ф = (М , Si, S2, • • •, Sk). Возьмем iV-мер-

ную матрицу F = [/,112. й , *2, • • •> W = 1, — , \Щ- Позиции

по каждому измерению ^-мерной матрицы перенумеруем числами

натурального ряда 1,2,..., |Af|. Каждой букве тп 6 М поставим

во взаимно однозначное соответствие номер из этого натурального

ряда и расположим буквы го; G М по соответствующим позициям

каждого измерения N -мерной матрицы. Каждый элемент

этой матрицы равен числу слов, в которые входят буквы, соответ

ствующие номерам *i, *2, ..., in - Одинаковые индексы в напи

сании не дублируем. Построенную таким образом матрицу будем

называть N-мерной частотной матрицей отношений или (если

нас не интересует размерность этой матрицы) частотной гипер

матрицей отношений.

Если среди индексов i'i, *2,..., tjv у элемента есть хотя

бы два индекса различного написания, то этот элемент называ

ется взаимной частотой соответствующих букв, в противном слу

чае — собственной частотой этих букв. Частота имею

щая к различных индексов, называется частотой к-го порядка.

При вычислении производной для пары элементов использова

лись частоты первого и второго порядка.

Производная dG/dS графа G по событию S на тройках эле

ментов:

9G.

— (та, ть, тс)

гфз, *ФЬ j ф к.

1т атьтс I

■■ 771 q

£ /< -

а уГПс

-]Г

fa + г -'$2 fijX

(з.ю)

tj= m a,rnb,mc i,j,k=m a,mb,mc /