Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§3.1. Взвешенный граф и его матричное задание

161

V3 Vi

«5

0 1 1

0 0

«1

1 1

0 0 0

1 1 1

0 0 0 0 0

1 Vi

ности 5(Ф) графа G, в которой диагональные элементы равны 1:

Минимизацию затрачиваемого количества информации при за

дании графа сведем к покрытию столбцов строками матрицы

Q (Ф). Для уменьшения трудоемкости поиска минимального по

крытия вычеркнем поглощаемые строки и столбцы. Строка а по

глощает строку (3, если множество столбцов Ма, покрываемых

строкой а, содержит множество столбцов Мр, покрываемых стро

кой /3, Ма D Мр. Столбец а поглощает столбец 6, если мно

жество строк Мь, покрывающих столбец Ь, содержит множество

строк Ма, покрывающих столбец а, Ма С Мь-

Найдем покрытие столбцов строками матрицы <3(Ф), затем

удалим недиагональные единичные элементы, вошедшие в покры

тие, и снова произведем покрытие столбцов и т. д. до тех пор, пока

все недиагональные элементы не будут равны нулю. В результате

получим минимизированное задание графа G в виде соответствую

щего мографа, в котором сигнатура представляет собой сечения

элементов полученных покрытий.

В рассматриваемом случае минимальное покрытие имеет вид

{t>3, ve}. Этому покрытию соответствуют две окрестности единич

ного радиуса: 0(v3) = { , v2, v4, v5} и 0(v6) = {v4, v5, v7}. Пос

ле удаления соответствующих единиц из матрицы <5(Ф) получаем

Матрицу

<?'(ф) =

0 1

«6 ,

0 1

которая имеет покрытие {vi, «2} или {«4, V5}. Для определен

ности выберем первое покрытие. Окончательно рассматриваемый

Граф G задается моделью Ф, матрица инцидентности которой име

ет вид

£ (* ) =

VI Vi Vi

1 1 1

t>3

—

1 1 1

«8

0 0

0 Vi

0 0

Для задания этой матрицы необходимо 20 бит вместо 49 бит

при задании этого графа матрицей смежности. Мограф GM (ф(Ф))

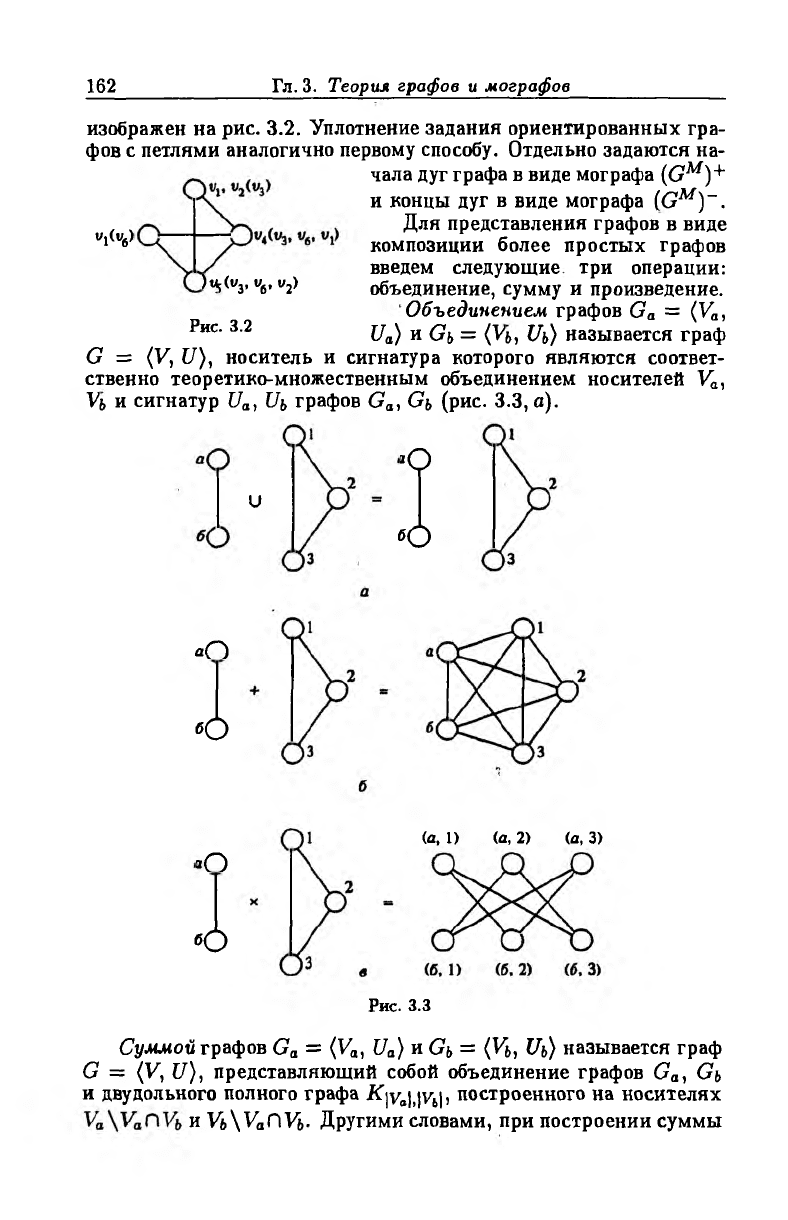
162

Гл. 3. Теория графов и мографов

изображен на рис. 3.2. Уплотнение задания ориентированных гра

фов с петлями аналогично первому способу. Отдельно задаются на

чала дуг графа в виде мографа (GM)+

и концы дуг в виде мографа (GM)~.

Для представления графов в виде

композиции более простых графов

введем следующие три операции:

объединение, сумму и произведение.

Объединением графов G„ = (Va,

Ua) и Gb = (Vf>, Ub) называется граф

G = (V, U), носитель и сигнатура которого являются соответ

ственно теоретико-множественным объединением носителей Уа,

Vb и сигнатур Ua, Щ графов Ga, Gb (рис. 3.3, а).

)u,(v3, v6, v2)

Рис. 3.2

* 0

аП

« 6

(а, 1) (а, 2) (а, 3)

Рис. 3.3

Суммой графов Ga = (Va, Ua) и Gb = (И, Щ) называется граф

G = (V, U), представляющий собой объединение графов Ga, Gb

и двудольного полного графа ^|v e|,|vt|, построенного на носителях

и Vb\VanVb. Другими словами, при построении суммы

§ 3.2. Связность и сильная связность графа 163

графов Ga и Gb определяется их объединение и каждая вершина

и,- € Va, не вошедшая в пересечение VaC\Vb, соединяется со всеми

вершинами И \ К П Ц,, и наоборот. Будем говорить, что вершина

v конусирует граф G, если она смежна со всеми вершинами графа

G. Вершины, не вошедшие в пересечение слагаемых V{ £ Va П Vb

при суммировании графов Ga и Gb, конусируют соответственно

Vb \ Va П И И Va \ Va П Vb (РИС. 3.3, б).

Декартовым произведением графов Ga = {[Va, Га) и Gb =

= (Vb, Гь) называется граф

G = (V, Г), V = Va xVb= {Ki, Vbt)/ vai e Va, vbi e Vb}, .

Г К < , Vbi) = Гиа< X ГиЬ;

(рис. 3.3, в).

§ 3.2. Связность и сильная связность графа

Распределение цепей, циклов в неориентированном графе и пу

тей и контуров в ориентированном графе определяет многие свой

ства графа, в том числе его связность и сильную связность.

Цепью называется последовательность ребер (pi, Р2, • • Рп)

вида pi = (Vi, v;+i), г = 1,2,..., п. Вершины цепи могут иметь сте

пень, равную 1. Вершина vx со степенью, равной 1, называется

концевой.

Число ребер цепи, соединяющей вершины Vi и vj, называется

ее длиной l(vi, Vj).

Циклом называется цепь, концевые вершины которой совпа

дают. Все вершины цикла имеют степень s(u,-) > 2.

Цепь называется: составной, если в ней повторяется хотя бы

одно ребро; сложной, если повторяется хотя бы одна вершина;

простой, если не повторяется ни одна вершина.

Граф G = (V, U) называется связным, если любая пара его

вершин соединена цепью.

Максимальный по включению вершин связный подграф графа

называется его компонентой связности. Граф называется несвяз

ным, если число его компонент больше одной. Например, граф, со

стоящий из двух несмежных вершин, является несвязным и имеет

две компоненты связности.

Рассмотрим алгоритм определения связности графа и числа его

компонент.

Теорема 3.1. Элемент матрицы Sn, где S = [s,j] — мат

рица смежности, Sij есть множество последовательных иден

тификаторов ребер, образующих цепь между и,- и Vj, предста

вляет собой множество цепей длины п, соединяющих вершины

Vi,Vj.

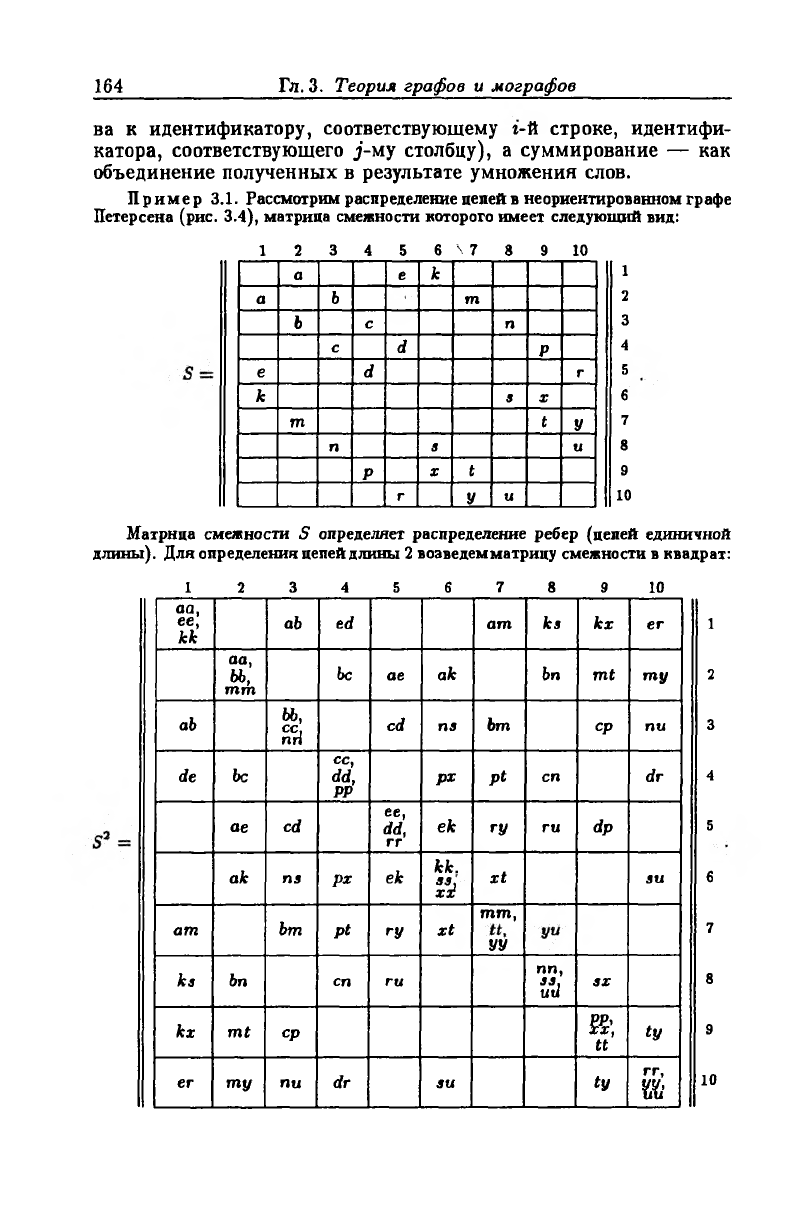
При возведении в n-ю степень матрицы смежности S = [s,j]

умножение рассматриваем как конкатенацию (приписывание спра-

164

Гл. 3. Теория графов и мографов

ва к идентификатору, соответствующему г-й строке, идентифи

катора, соответствующего j -му столбцу), а суммирование — как

объединение полученных в результате умножения слов.

Пример 3.1. Рассмотрим распределение цепей в неориентированном графе

Петерсена (рис. 3.4), матрица смежности которого имеет следующий вид:

Матрица смежности S определяет распределение ребер (целей единичной

длины). Для определения цепей длины 2 воаведемматрицу смежности в квадрат:

123456789 10

аа,

ее,

кк

аа,

bbt

be ae

bn mt my

bb,

cd ns bm cp nu

de be

ccy

ddt

ее,

dd,

ru dp

ak пз

кк.

am bm pt

mm,

УУ

ks bn cn

nn,

33 .

uti

er my

rr,

1 2 3 4 5 6 \ 7 8 9 10

a e

a b

e d r

3 X

m t

3 и

X t

§ 3.2. Связность и сильная связность графа 165

Суммируя матрицы S + S2, получаем, что в

результирующей матрице отсутствуют нулевые эле

менты, что означает существование цепи длины 1

или длины 2 между любой парой вершин графа Пе

терсена. Следовательно, граф Петерсена связный и

представляет собой компоненту связности.

Понятие цепи является Основным при

изучении метрических свойств графа.

Минимальная длина цепи, соединяю

щей вершины V{ и vj,называется расстоя

нием r(vi, Vj) между вершинами у,-, Vj:

r(vi, vj) = min lk(vi, Vj).

Максимальное расстояние между вершинами графа G называ

ется диаметром графа d(G):

d(G) = m axm inи,),

tj к

Введенная на множестве всех вершин (и,-, Vj) графа G функция

f(v{, Vj) определяет его метрику. Действительно, эта функция

vj) удовлетворяет следующим трем аксиомам:

(Vvi, vj)(r(vi, Vj) - О) <-> v{ = vj;

(Vvi, vj)(r(vi, Vj) = r(vj, Vi));

(VVi, Vj, vk)(r(vi, Vj) + r(Vj, vk) > r(vi, ujt));

последнюю аксиому обычно называют неравенством треуголь

ника.

• Матрица А называется к-клеточной, если в результате пере

становки строк и столбцов она приводится к виду

0 ... 0

0 0

Аз

... 0

0 0

... Ak

Ще матрица A,-, t = 1, ..., к, не содержит ни одного нулевого эле

мента (кроме, быть может, диагональных).

Теорема 3.2. Граф G состоит из к компонент связности

тогда и только тогда, когда его матрица достижимости

d(G)

0 ( G ) = £ [ S (G ) ] \ (3-2)

t=l

S(G) — матрица смежности, d(G) — диаметр графа G,

Шляется к-клеточной.

166

Гл. 3. Теория графов и мографов

Цикл называется эйлеровым, если каждое ребро графа участ

вует в его образовании один раз; граф, содержащий такой цикл,

называется эйлеровым.

Теорема 3.3. Граф G = {V, U) является эйлеровым тогда

и только тогда, когда он связен и степень s(va) каждой вер

шины va € V — четное число.

Простой цикл называется гамильтоновым, если он проходит

через каждую вершину графа; граф, содержащий такой цикл, на

зывается гамильтоновым. Теорема 3.3 определяет простой кри

терий выявления свойства эйлеровости для каждого графа. Для

определения свойства гамильтоновости графа имеется следующее

достаточное условие.

Теорема 3.4 (Дирак). Если граф G = (V, U), W \ > 3, яв

ляется связным и степень каждой вершины ui € V есть

где [ ] — ближайшее целое число, то граф является гамильто

новым.

Граф, состоящий из одной вершины, называется тривиаль

ным. Удаление вершины из нетривиального графа G приводит к

подграфу G\v, содержащему все вершины графа G, кроме v, и

все ребра графа G, не инцидентные и. Аналогично, удаление ребра

х приводит к подграфу, содержащему все вершины (к остовному

подграфу) и ребра, за исключением ребра х, т. е. G\x. Минималь

ную степень вершин графа обозначают 6(G) = mms(v,), и,- € G.

Если все вершины графа имеют одинаковую степень п, то такой

граф называют регулярным графом степени п.

Связностью графа x(G) называется наименьшее число вер

шин, удаление которых делает граф несвязным, или тривиаль

ным. Из этого определения следует, что для любого графа x(G) >

> 0. Полный граф К п становится тривиальным, если удалить

п - 1 вершин, и поэтому х(Кп) = п — 1.

Если x(G) = п, то граф G называют п-связным.

Реберной связностью A(G) графа G называется наименьшее

количество ребер, удаление которых приводит к несвязному, или

тривиальному графу. Для несвязного, или тривиального графа

A(G) = 0.

Для любого графа G связность, реберная связность и мини

мальная степень связаны следующим неравенством:

Среди всех графов с п вершинами и т ребрами наибольшая

связность равна 0, если т < п —1, и равна [2тп/п], если т > п — 1,

где скобки [ ] означают, что берется целая часть выражения.

«(«.■)> \\У \

(3.3)

X(G) < A(G) < 6(G).

(3.4)

§ 3.2. Связность и сильная связность графа 167

Простые цепи называются реберно непересекающимися, если

никакие две из них не имеют общего ребра. Бели же у таких цепей

нет и общих вершин, то они называются вершинно непересекаю-

щимися.

Пусть G — связный граф, а и, v — две различные его вершины.

Множество ребер Е графа G называется и, v-разделяющим мно

жеством в G , если любая простая цепь из « в и содержит ребро

из Е. Множество вершин V графа, не содержащее «, и, называется

и, v-отделяющим множеством в G , если любая простая цепь из

v b v проходит через вершину V.

Если некоторое «, «-разделяющее множество Е содержит к ре

бер, то число реберно непересекающихся простых цепей из и в v не

может превысить к, поскольку иначе число ребер из Е должно при

надлежать более чем одной простой цепи. Бели и, и-разделяющее

множество имеет наименьшую мощность, то число реберно непе

ресекающихся простых цепей между « н и равно к.

Теорема 3.5. Максимальное число реберно непересекаю

щихся простых цепей, соединяющих две различные вершины и,

v связного графа G , равно минимальному числу ребер в и, v-раз

деляющем множестве.

Теорема 3.6. Максимальное число вершинно непересекаю

щихся простых цепей, соединяющих две различные несмежные

вершины и, v графа G, равно минимальному числу вершин в и, v-

отделяющем множестве.

Теорема 3.7. Граф п-связен тогда и только тогда, когда

любая пара его вершин соединена по крайней мере п вершинно

непересекающимися цепями.

Теорема 3.8. Граф п-реберно связен тогда и только тог

да, когда любая пара его вершин соединена по крайней мере п

реберно непересекающимися цепями.

Теорема 3.9 (Менгер). Для любых двух множеств вершин

Va, V/з (Уа, Vp ф 0 , VaC\Vp = 0) наибольшее число непересекаю

щихся цепей, соединяющих Va и Vp, равно наименьшему числу

вершин, отделяющих Va и Vp.

Теоремы 3.5-3.9 определяют зависимость связности графа от

числа непересекающихся цепей. Эту зависимость впервые иссле

довал Менгер.

Разделяющим множеством связного графа G называется та

кое множество его ребер, удаление которых из G делает его несвяз

ным. Например, множество {р7, pg, Ps, рз} на рис. 3.5, о является

разделяющим, и его удаление приводит к образованию двух ком

понент связности.

Разрезом называется такое разделяющее множество, которое

не имеет собственного разделяющего подмножества. Множество

{р7, pg, ре, рз} не является разрезом, поскольку оно содержит раз

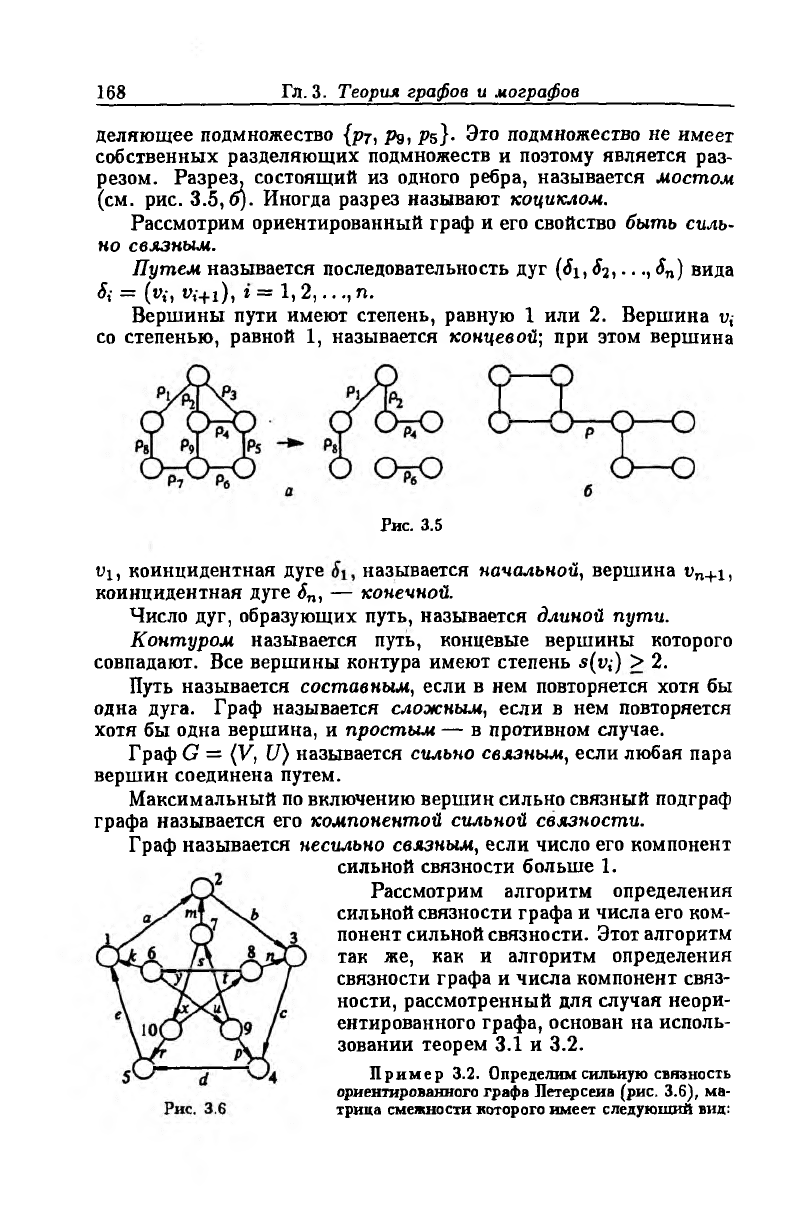
168

Гл.З. Теория графов и мографов

деляющее подмножество {pr, Рд, Ps}- Это подмножество не имеет

собственных разделяющих подмножеств и поэтому является раз

резом. Разрез, состоящий из одного ребра, называется мостом

(см. рис. 3.5, б). Иногда разрез называют коциклом.

Рассмотрим ориентированный граф и его свойство быть силь

но связным.

Путем называется последовательность дуг (£i, £2,..., Sn) вида

8{ = (у,-, у1+х), * = 1,2, ...,п.

Вершины пути имеют степень, равную 1 или 2. Вершина и;

со степенью, равной 1, называется концевой; при этом вершина

Рис. 3.5

«1, коинцидентная дуге называется начальной, вершина Vn+i,

коинцидентная дуге Sn, — конечной.

Число дуг, образующих путь, называется длиной пути.

Контуром называется путь, концевые вершины которого

совпадают. Все вершины контура имеют степень в(у,-) > 2.

Путь называется составным, если в нем повторяется хотя бы

одна дуга. Граф называется сложным, если в нем повторяется

хотя бы одна вершина, и простым — в противном случае.

Граф G = (V, U) называется сильно связным, если любая пара

вершин соединена путем.

Максимальный по включению вершин сильно связный подграф

графа называется его компонентой сильной связности.

Граф называется несильно связным, если число его компонент

сильной связности больше 1.

Рассмотрим алгоритм определения

сильной связности графа и числа его ком

понент сильной связности. Этот алгоритм

так же, как и алгоритм определения

связности графа и числа компонент связ

ности, рассмотренный для случая неори

ентированного графа, основан на исполь

зовании теорем 3.1 и 3.2.

Пример 3.2. Определим сильную связность

ориентированного графа Петерсена (рис. 3.6), ма

трица смежности которого имеет следующий вид:

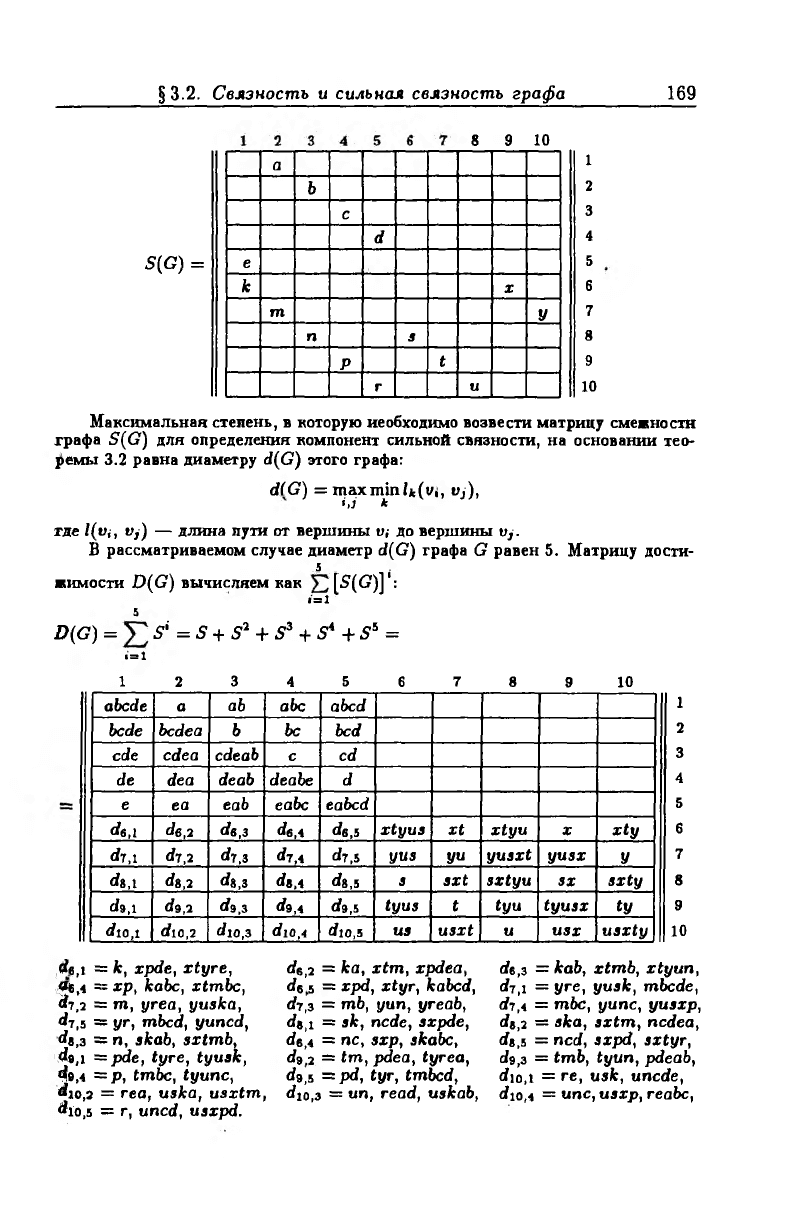
§ 3.2. Связность и сильная связность графа

169

8 9 10

5(G) =

n 3

Максимальная степень, в которую необходимо возвести матрицу смежности

графа 5(G) для определения компонент сильной связности, на основании тео

ремы 3.2 равна диаметру d(G) этого графа:

d(G) = maxminlk(v>, vj),

i,j к

где l(vi, Vj) — длина пути от вершины и,- до вершины Vj.

В рассматриваемом случае диаметр d(G) графа G равен 5. Матрицу дости-

жимости D(G) вычисляем как [5(G)]1:

*=2

D(G) = S‘ = S + S2 + 53 + S* + 5s =

i=i

123456789 10

a b ed e

a a b

a b c

a b e d

b e d e

b e d e a

b b e b e d

c d e

c d e a c d e a b

с c d

d e d e a d e a b

d e a b e

e e a ea b

e a b c

e a b e d

d e, l d e, 2

d e, з

d e , 4 d e,s

x t y u s

x t

x t y u

x t y

d i , i

d i,2

d f ,3

d j,4

d r ,5

y u s

Уи

y u s x t

y u s x

^8,1

d »,2 db,3

d s , 4

dg,5

3 3 X t s x t y u

s x

s x t y

^9,1

d a ,2

da,3

d a ,4

de,s

t y u s t

t y u t y u s x

t y

^10,1

d 10,2

dio,3 d io ,4

dw,5

из u s x t и

U SX

U 3 X ty

#e,i = fc, arpcfe, xtyre,

«8,4 as xp, it a be, xtmbc,

#1,2 = m, yrea, yuska,

d7,s = yr, mbed, yuncd,

dt,з = n, jfcab, sxtmb,

d*,i = pde, tyre, tyuik,

4»,4 = p, tmbc, tyunc,

^10,3 = rea, uska, usxtm,

dio,s = r, uncd, utxpd.

dg,2 = ka, xtm, xpdea,

<f6s = xpd, xtyr, к abed,

di,3 = mb, yurt, yreab,

ds,i = afc, nccfe, sxpde,

de,i = nc, sxp, skabc,

d9 2 = tm, pdea, tyrea,

d9,s = pd, tyr, tmbed,

dio,з = un, read, uskab,

de,з = kab, xtmb, xtyun,

dr.i = yre, уизк, mbede,

dr,4 = mbc, yunc, уизхр,

ds,2 = »fca, ixtm, ncdea,

rfg,5 = ncd, sxpd, sxtyr,

dg,з = tmb, tj/un, pdeab,

dio,i = re, usfc, uncde,

d 10,4 = unc, изхр, reabc,

170

Гл.З. Теория графов и мографов

Компоненте сильной связности в матрице достижимости соответствует под

матрица максимального размера, каждый элемент которой не равен О. Элемен

ты, показывающие связь между этими подматрицами, могут быть не равны 0.

В данном примере имеем две компоненты сильной связности с носителями

соответственно {1, 2, 3, 4, 5} и {6, 7, 8, 9, 10}.

Сетью называется ориентированный граф G = (V,U), в кото

ром выделены два множества полюсных вершин, У+ и V~, таких,

что из каждой вершины vf € V+ дуги только исходят, в каждую

вершину v~ £ V~ дуги только входят и каждая вершина и, €

6 V \ (У+ U V~) коинцидентна как входящим, так и исходящим

дугам. Сопоставим каждой дуге положительное число, определяю

щее ее “пропускную способность”. Тогда можно сформулировать

еще один вариант теоремы Менгера для такого взвешенного по

дугам ориентированного графа.

Теорема 3.10. Максимальный поток через сеть равен ми

нимальной пропускной способности ее разреза.

Алгоритм определения максимального потока рассмотрен в

§3.5.

§ 3.3. Цнкломатнка и коцикломатика

Для исследования циклов в графе используют цикломатиче-

скую матрицу C(G) = [c,j]: каждому циклу графа взаимно од

нозначно сопоставляется вектор-строка матрицы C(G)\ каждый

элемент этой строки определяется как

_ Г1, если j-e ребро входит в г-й цикл,

C,J “ 1.0 в противном случае.

Множество C(G) всех векторов, каждый из которых соответ

ствует одному циклу графа G, образует векторное пространство,

называемое пространством циклов графа G. При этом выпол

няются следующие условия:

1) для любых двух циклов Ri, Rj € C(G), Ri П Rj ф 0 , суще

ствует некоторый третий цикл (Ri ф Rj) £ C(G), где ф означает

поразрядное сложение по модулю 2;

2) сложение по модулю 2 обладает свойством коммутативности,

т. е. для любых двух Ri, Rj € C(G)

Ri ф Rj ~ Rj ф Ri;

3) сложение по модулю 2 ассоциативно, т. e. для любых Ri,

Rj, Rk € C(G)

(Ri ф Rj) Ф Rk ~ Ri Ф (Rj Ф Rk)•

Базисом векторного пространства называется всякая сис

тема линейно независимых векторов, порождающая данное про

странство. Множество векторов тогда и только тогда является ба

зисом векторного пространства, когда всякий элемент этого