Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§ 2.7. Исчисление высказываний

131

Покрытие ядериое, следовательно, оно одно. В общем случае алгоритмом

]1етрнка порождаем все покрытия таблицы Q.

3. Удаляем из каждого покрытия любой элемент. С учетом свойства кри-

хячности покрытия очевидно, что it/fi является непротиворечивой системой.

Цроведя возможные удаления из покрытий, получаем все множество непроти

воречивых секвенционных систем.

Для исследуемого случая имеем четыре непротиворечивые секвенциальные

системы: 1) тг//2; 2) ir//5; 3) ж //7; 4) ir/ft.

Вычисляем непротиворечивые антецеденты.

1) & /( — 0101000001010000,

' «=5,7,8

& /,

1* 5,7,8 '

= Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V X1X2X3X4 =

: Х1Х2Х4 V Х1Х2Х4 = Х2Х4.

На основании истинности этого антецедента заключаем, что результат ми

нерализации нерудного тела — доломит,

барит, кальцит — проявляется в зоне с

азимутом падения от 271° до 360°.

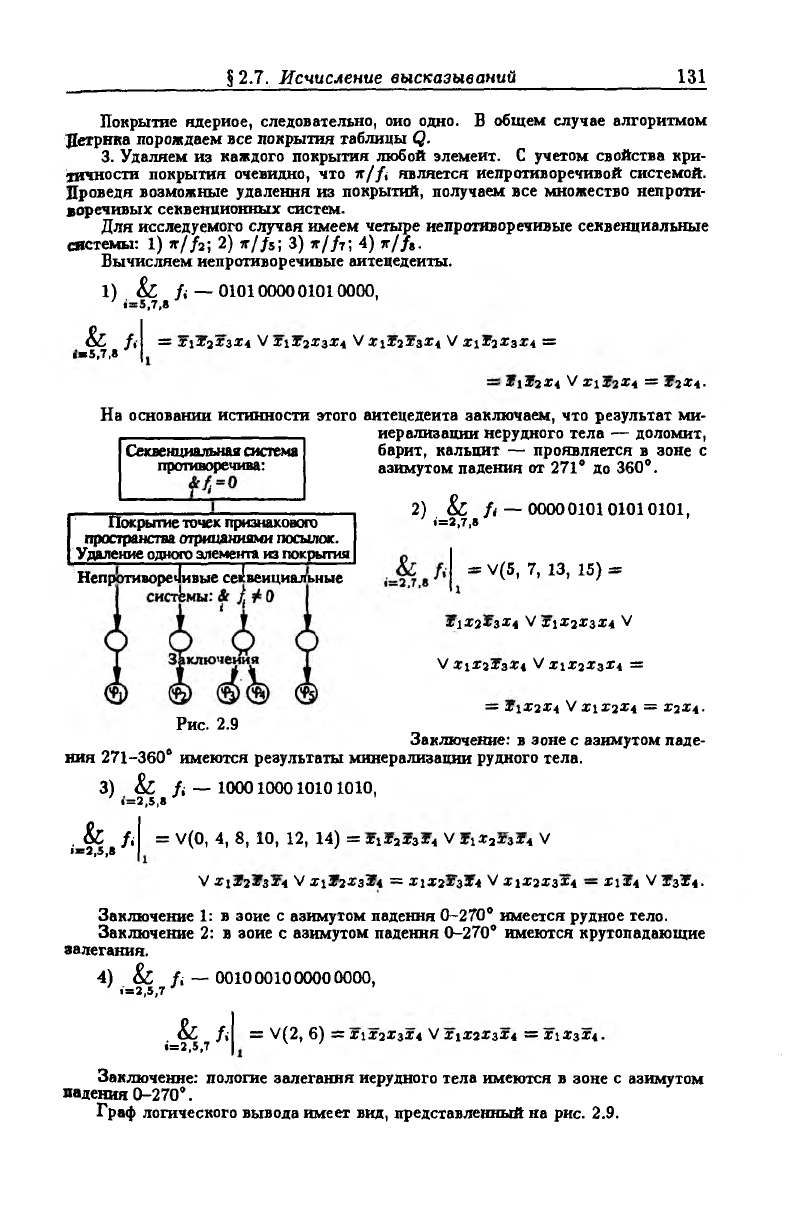
Секвенциальная система

противоречива:

Покрытие точек признакового

пространства отрицаниями посыпок.

Удаление одного элемента из покрытия

НепротивореЛивые секвенциальные

2) & / , — 0000010101010101,

' <=а,7,* '

= V(5, 7, 13, 15) =

Рис. 2.9

Х1Х2Х3Х4 V Х1Х2Х3Х4 V

V Х1Х2Х3Х4 V Х1Х2Х3Х4 =

= Х1Х2Х4 V Х1Х2Х4 = Х2Х4.

Заключение: в зоне с азимутом паде

ния 271-360° имеются результаты минерализации рудного тела.

3) Sz.fi — 100010001010 1010,

«=2,5,8

. & fi

»«2,5,в

= V(0, 4,

, 10, 12, 14) = Х

V Х

V Х1Х2Х3Х4 V Х1Х2Х3Х4 = ЦХ2Х3Х4 V Х1Х2Х3Х4 — Х1Х4 V Х3Х4.

Заключение 1: в зоне с азимутом падения 0-270° имеется рудное тело.

Заключение 2: в зоне с азимутом падения 0-270° имеются крутопадающие

залегания.

4) & и — 0010001000000000,

««2,5,7 4

. & U

•=2,5,7

= V(2, 6) = Х1Х2Х3Х4 V Х1Х2Х3Х4 = Х1Х3Х4.

Заключение: пологие залегания нерудного тела имеются в зоне с азимутом

падения 0-270°.

Граф логического вывода имеет вид, представленный на рнс. 2.9.

132

Гл. 2. Математическая логика

Каждое заключение ip, представляет собой конъюнкцию сукцедента. Из со

вместного анализа пяти заключений имеем общий логический вывод: в зоне с

азимутом падения 0-270° имеется крутопадающее залегание рудного тела.

§ 2.8. Конечнозначные логики

Обобщением двузначных логик являются конечнозначные ло

гики.

Функция f(x 1, Х2, ..., хп), отображающая n-мерный А;-знач-

ный кортеж (<Ti, сг2, ..., сгп), <т, € {0, 1, . . к - 1}, t = 1, 2, ..., п,

во множество {0, 1, . . к — 1}, называется функцией к-значной

логики. Будем задавать функцию Л-значной логики f(x i, х2, ...

. . хп) с помощью таблицы истинности (одномерной таблицы),

число строк которой равно кп, или двумерной таблицы, число кле

ток которой равно кп.

Рассмотрим трехзначную функцию — функцию Вебба, задан

ную табл. 2.33, 2.34.

Т абли ца 2.33 Т абли ца 2.34

Ха

хь

0 1

1 2

0 2 0

1 0

1 1 2

1 2

2 0 0

1 0

2 2 0

Ха

хь

0 1

2 0

0 0

Функция Вебба

у = ха о хь = шах (х0, хь) -f l(mod к)

является полной в конечнозначной логике. Таким образом, конеч

нозначная алгебра Вебба

АВ -(М , о,), М = {1, 2, к - 1},

определяет соответствующую логику.

Другими часто встречающимися А;-значными логиками явля

ются логики, определяемые:

алгеброй Поста

Ап = (М, V, ~), М = {0, 1,2, ...,к- 1},

где ха V хь = шах(ха, хь) — дизъюнкция, х = х -f l(modA;) —

цикл;

алгеброй Россера—Тьюкетта

Арт = (М , V, &, ji, г), М - {0, 1 ,2 , ... ,* - 1},

§2.8. Конечнозначные логики 133

где х„ & хь = min (ха, хь) — конъюнкция,

. , ч f к - 1, х = *,

* м = ( о ,

— характеристические функции г = 0, 1, ..., к — 1.

Сигнатура любой алгебры должна быть полной, независимой и

непротиворечивой. Сигнатура является полной, если любая дру

гая формула может быть представлена в виде пропозициональной

формы с помощью ее элементов.

Сигнатура называется независимой, если в ней не найдется

элемента, выводимого с помощью правил вывода из других эле

ментов сигнатуры.

Сигнатура непротиворечива, если не найдется формулы F,

которая справедлива вместе с формулой F.

Конечнозначные логики являются обобщением двузначных ло

гик. Например, логика Поста (М , V, ~) обобщает логику Буля

(М , V, ").

При минимизации логических функций конечнозначных ло

гик можно использовать результаты двузначной логики — теорию

ДНФ булевых функций. Для этого введем булеву переменную хга)

равную 1 при ха = г и 0 в противном случае, ха ф г. Будем назы

вать х*а i-й фазой переменной ха, ха = {0, 1, ..., к — 1}:

<=U; <2-23)

Отрицание г-й фазы равно дизъюнкции остальных фаз этой

переменной:

fc-i

х'а = V х3а.

;=°

Очевидно, что

х° V х1 V ... V xfc_1 = 1.

сх v ~ot 4 4 а

Действительно,

V (xl v x l V . . . V * * - 1) = х°а V х°а = 1.

Используя введенное высказывание х'а, рассмотрим миними

зацию трехзначной функции Вебба, заданной табл. 2.33, 2.34:

у = ха о хь, у0 = x°x2b V х\х\ V х2ах% V x2axl V x*xg.

Согласно законам коммутативности, идемпотентности, ассоци

ативности и дистрибутивности имеем

У° = (х°а V xi V х2а)х2ь V x2a(x°b V х\ V х2ь) = 1 • х2ь V х2 • 1 = х2 V х2ь.

134

Гл. 2. Математическая логика

Этот же результат можно получить, сравнивая тройки конъ

юнкций для определения истинности выражения (2.23) после

применения закона дистрибутивности

(рис. 2.10). Каждая конъюнкция соответ

ствует максимальному интервалу — ре

бру. Ответ на вопрос о том, можно ли

минимизировать полученную сложность

функции, получаем, строя и покрывая та

блицу Квайна (табл. 2.35).

Таблица 2.35

Максимальные

Интервалы

интервалы

12 20 21 22

-2

1 1

Имеем одно покрытие ж = {2-, —2}, которому соответствует

минимальная ДНФ нулевой фазы трехзначной функции Вебба

у0 = х2а Ч х2ь.

Аналогично получаем минимальные формы для 1-й и 2-й фаз

функции у = ха охь

,.1 _ го_о

У — хахь,

2 = x°xl V xjx? V xlxl

а*Ь

Таким образом, минимизация функции А;-значной логики сво

дится к минимизации системы, состоящей из к булевых функций,

каждая из которых определяет соответствующую фазу этой функ

ции.

При минимизации логических функций {/,-} уменьшается

коэффициент связности соответствующего мографа

Коэффициентом связности графа S(G) называется отношение

мощности сигнатуры к мощности носителя этого графа. Коэффи

циент связности мографа определяется как коэффициент связно

сти графа, полученного в результате снятия его моделизации.

Неминимизированная функция Вебба определяется моделью

вида

Ф1 = (М, S3>, М = {х°, х\, х2, xj, у0, у1, у2},

S3 = { {х°а, х°ь, у1}, {з;°, х\, у2) , {х°, х2ъ, у0},

{х\, х°ь, у2}, {xl xl, у2}, {xl х2, у0},

§2.8. Конечнозначные логики 135

Мограф GI*, определяемый этой моделью, изображен на

рис. 2.11, а. Его коэффициент связности S(G ^) равен 2|:

о (пМ \ 2 + 6 + 6-{-4 + 5-{-5 + 6 + 4 + 4 1

* 1 ’ ~ 2-9 3‘

Эта функция после минимизации соответствует модели Ф2 вида

Ф2 = (М, S2, S3>, М = {г?, х\ , х£, xj, xjj, у0, у1, у2},

■S2 { { x 2, У °> , {* & , У0 } } ,

3 4 5 6

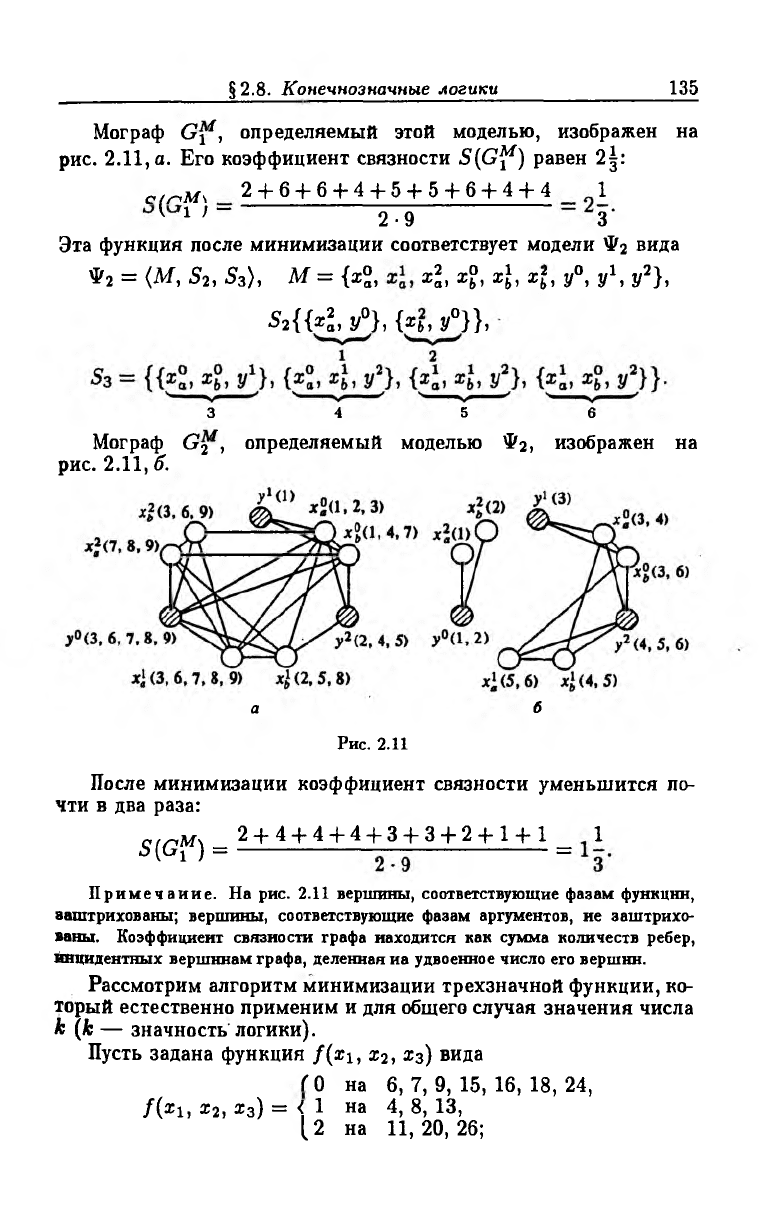
Мограф G21, определяемый моделью Ф2, изображен на

рис. 2.11, б.

а б

Рис. 2.11

После минимизации коэффициент связности уменьшится по

чти в два раза:

с (r<M\ 2 + 4 + 4 + 4 + 3 + 3 + 2 + 1 + 1 1

5 (0 ‘ >

------------------------------------------------=

П рим ечание. На рис. 2.11 вершины, соответствующие фазам функции,

заштрихованы; вершины, соответствующие фазам аргументов, не заштрихо

ваны. Коэффициент связности графа находятся как сумма количеств ребер,

Инцидентных вершинам графа, деленная иа удвоенное число его вершин.

Рассмотрим алгоритм минимизации трехзначной функции, ко

торый естественно применим и для общего случая значения числа

к (к — значность логики).

Пусть задана функция f(xi, х2) хз) вида

ГО на 6,7 ,9,15,16,18,2 4,

/(х 1, х2, х3) = < 1 на 4, 8, 13,

[2 на 11,20,26;

136

Гл. 2. Математическая логика

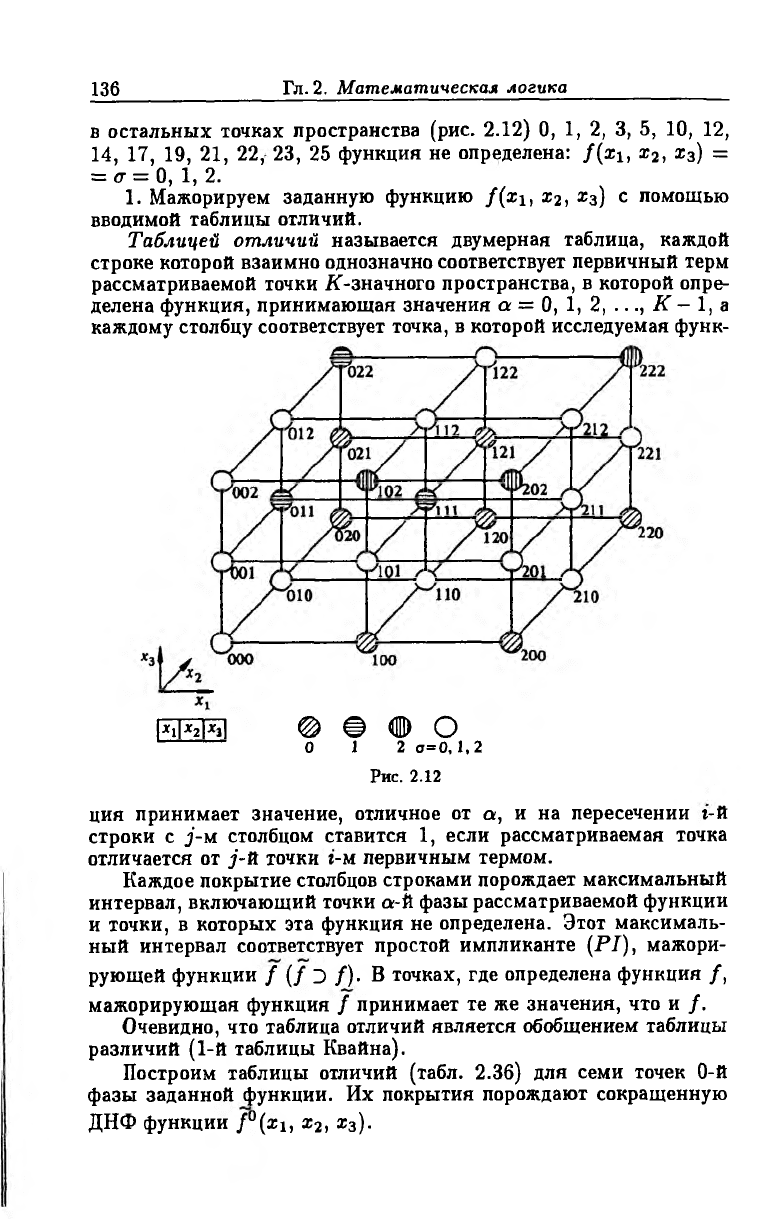
в остальных точках пространства (рис. 2.12) 0, 1, 2, 3, 5, 10, 12,

14, 17, 19, 21, 22, 23, 25 функция не определена: f(xь х2, х3) =

= а = 0, 1, 2.

1. Мажорируем заданную функцию f(xi, х2, х3) с помощью

вводимой таблицы отличий.

Таблицей отличий называется двумерная таблица, каждой

строке которой взаимно однозначно соответствует первичный терм

рассматриваемой точки iif-значного пространства, в которой опре

делена функция, принимающая значения а = 0, 1, 2, ..., К - 1, а

каждому столбцу соответствует точка, в которой исследуемая функ-

Ч Ч Ч 0 0# О

О 1 2 ст=0,1,2

Рис. 2.12

ция принимает значение, отличное от а, и на пересечении г-й

строки с j- м столбцом ставится 1, если рассматриваемая точка

отличается от j-tt точки г-м первичным термом.

Каждое покрытие столбцов строками порождает максимальный

интервал, включающий точки а-й фазы рассматриваемой функции

и точки, в которых эта функция не определена. Этот максималь

ный интервал соответствует простой импликанте (P I), мажори

рующей функции / ( / Э /). В точках, где определена функция /,

мажорирующая функция / принимает те же значения, что и /.

Очевидно, что таблица отличий является обобщением таблицы

различий (1-й таблицы Квайна).

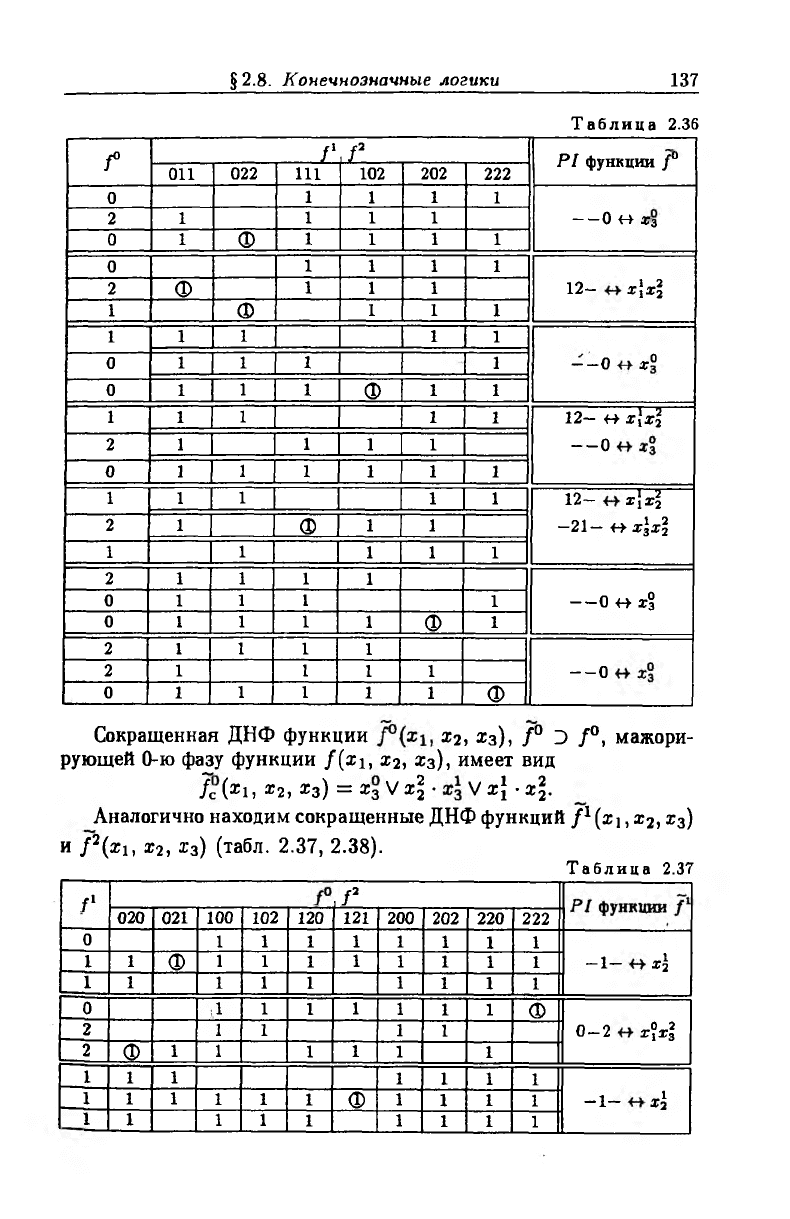
Построим таблицы отличий (табл. 2.36) для семи точек 0-й

фазы заданной функции. Их покрытия порождают сокращенную

ДНФ функции f°(x 1, х2, х3).

§ 2.8. Конечнозначные логики

137

Т абли ц а 2.36

/' / 2

PI функции /°

011 022 111 102

202

222

1 1 1 1

----

0 <->■ Хз2 1

1 1 1

0 1

1 1 1 1

1 1 1

12— х\х%2

1 1 1

1 1

- - 0 х°

О 1 1

1 1

1 12— f* xjx]

----

2 1

1 1

О 1

1 1 1

1 1

12— х\х\

—21— ++ х|х|

2 1

1 1

2 1 1 1

---

Of»i§

0 1

1 1

0 1 1 1

2 1 1 1

- - 0

2 1 1

1 1

Сокращенная ДНФ функции х2, х3), f° Э /°, мажори

рующей 0-ю фазу функции /(х*, х2, Хз), имеет вид

/с (*1> * 2, хз) = *з V х\ • V х\ • х\.

Аналогично находим сокращенные ДНФ функций / х(хь х2, х3)

и f2(x 1, х2, х3) (табл. 2.37, 2.38).

Т абли ца 2.37

f l

/ 2

020 021

100 102

120

121

200 202 220

222

1 1

—1— x\

1 1

0 1 1

1 1

0-2 x?x|

1 1

1 1 1

1 1

-1 — x\

1 1

1 1 1

138

Гл. 2. Математическая логика

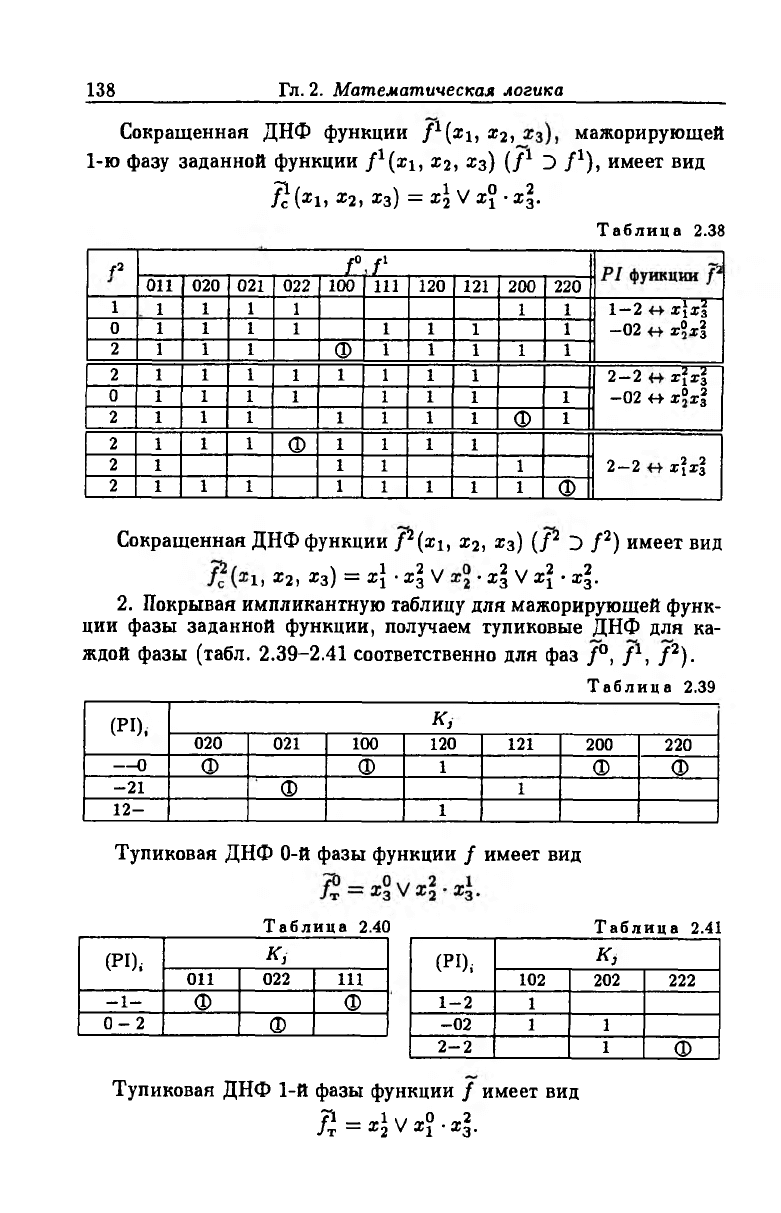
Сокращенная ДНФ функции fx(x\, х2, мажорирующей

1-ю фазу заданной функции fx(x\, х2, Хз) (/1 Э Z1), имеет вид

Л (*i. *2, жз) = х\ VxJ-x^.

Т абл ица 2.38

f 1

Oil 020 021

022 100

111

120

121

200 220

1 1

1—2 x\xl

1 1 1

1 1 1 1 1

—02 x°xl

1 1

2—2 xjxl

1 1 1

1 1 -02 <-► x°xl

1 1

1 1 1

1 1

2—2 xfxi

1 1

Сокращенная ДНФ функции f2(xi, х2, х3) (/2 э / 2) имеет вид

1, х2, х3) = х\ • х^ V • х\ V xj • х\.

2. Покрывая импликантную таблицу для мажорирующей функ

ции фазы заданной функции, получаем тупиковые ДНФ для ка

ждой фазы (табл. 2.39-2.41 соответственно для фаз /°, f1, / 2).

Т абли ц а 2.39

(PI),

020 021

100

120

121

200

220

—0

Ф Ф

-21

12-

Тупиковая ДНФ 0-й фазы функции / имеет вид

Т аблица 2.40

__________________ Т абли ца 2.41

(PI)i

к,

Oil 022

111

-1 -

0 -2

(PI).

102 202

222

1-2

-02

1 1

2-2

Тупиковая ДНФ 1-й фазы функции / имеет вид

Л = xjvx?-x|.

§2.8. Конечнозначные логики

139

Тупиковые ДНФ 2-й фазы заданной функции / имеют вид

72 — „1 - ~2 W „2 . „2 _ 7*0 . „2 72 _ ^0 . „2

/т2 Х2 ' Х3 ^ Х1

2 ~ 2.

Х3>

& = х\-х2зУЧ-Ч = Щ-*1 Я

в табл. 2.39-2.41 ifj и (-Р/),' — j -я конституента соответствую

щей фазы и i-я простая импликанта мажорирующей ее функции

соответственно.

В точках неопределенной области фазы мажорирующей функ

ции / ( / Э /) могут пересекаться, так как они соответствуют

нереализуемым ситуациям. В нашем примере 0-я и 1-я фазы (/°

и f1) пересекаются в точках 010, 110, 210; 1-я и 2-я фазы — в

точках 112 и 212.

Минимизированная функция f(xi, х2, Хз) определяется одной

из двух систем:

Л* = *з V х\х\ , = х\ V х?*2, Д = х\х\ V х?х2

или

/т2 = *3 V Х2Х3> # 2 = *2 V Х1Х1, /г2 = *2*3 V *1*3-

Рассмотрим уменьшение коэффициента связности К св могра-

фов, определяющих совершенную, сокращенную и тупиковые

ДНФ заданной функции f(x i, х2, х3).

(9,15,16,13,11)

*0(6, 7, 4, 8) /-N 24. 20. 26)

/°(6,7,9, 15,16,18, 24)

х\(Ь, 7,15,16, 24,8, 26)

с? (8, 11,20, 26)

х°(6, 9, 15,18, 24)

4(7,16, 4,13)

Рис. 2.13

Мограф G^B(f), определяющий совершенную ДНФ функции

f(x 1, х2, х3), представлен на рис. 2.13. Роль идентификаторов на

рисунке выполняют эквиваленты соответствующих троичных на

боров.

Коэффициент связности K CB(G^B) равен 3,25:

и (пМ ч 7 + 9 + 6 + 6 + 4 + 9 + 7 + 6 + 6 + 54-6 + 7

140

Гл. 2. Математическая логика

Сокращенная ДНФ функции f(x 1, х2, хз) определяется систе

мой вида ~ ~

/с = *з V х\ • z$ V х\ • Д1 = z j V х? •

Jl - х\ • V х% • V х\ ■ х\.

Произведем логическое умножение каждого выражения на ее

левую часть и логически сложим эти три выражения; в результате

получим мажорирующую функцию

7(*1, *

, *з) = / М V 7°*2*3 V Л**

1*2

V Л

С d

71^0^2 w 72^1 2 ,

V ^ 1®з V /Щ ^ з V /М * з V

с k т р

определяющую мограф (рис. 2.14).

Коэффициент связности мографа G™, определяющего сокра

щенную ДНФ функции f(x 1, Х2, х3), равен 1,25:

tfo (G f)

2 + 2+ 2+ 2 + 1 + 3 + 2 + 5 + 1 + 4 + 3 + 3

2 -12

= 1,25.

Аналогично вычисляем коэффициенты связности мографов,

определяющих тупиковые ДНФ функции f(xi, х2, ®з). Мажори-

х\(с, к)

рующая функция f(xi, х2, Хз), определяемая первой тупиковой

ДНФ, имеет вид

fT i(xi, х2, х3) = f%iX%V f^xlxlv ^ х \ V

'2 _2_2