Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§ 2.2. Разложение Шеннона. Декомпозиция булевых функций 101

где [ ] — целое ближайшее число; Na — число различных строк

таблицы Вейча (число остаточных булевых функций строч

ного разложения), каждая пара которых , ц>{2 не находит

ся в отношении включения: y?tl <f_ Щ — число различных

столбцов таблицы Вейча (число остаточных булевых функций

{<Pj} столбцевого разложения), попарно не находящихся в от

ношении включения: £ y?j2.

Пример 2.3. Рассмотрим построение декомпозиции булевой функции

f(x 1, Х2, . . xs), заданной табл. 2.5. Остаточные функции строчного разложе

ния (ро, <р 1 и <р2, <рз находятся в отношении включения: <ро Э <pi, <Р2 Э <рз;

объединяя соответствующие строки, получаем табл. 2.8.

Таблица 2.8

Х1Х2

X3XiXs

0 1

2 3

6 7

0,1

1 1

0 1 1 1

2,3

0 0

1 0 0

Отсюда получим Na = 2, к = 2, [log2 2] < 2. Следовательно, можно вместо

двух терминальных переменных, xi и Х2, ввести функциональную переменную

ifii и, кодируя первую строку в табл. 2.8 нулем, вторую — единицей, получить

зависимость

V i(* it *2 )|i = V(2, 3).

Аналогично, объединяя столбцы {0, 1, 2, 4, 6, 7}, {3} и {5}, получаем таб

лицу Вейча в виде табл. 2.9.

Таблица 2.9

<Pi

X3XiXs

0,1, 2,4,6, 7 3

1 0

0 0

Отсюда получим Nb = 3, S — 3, pog2 3] < 3.

Три полученных различных столбца кодируем, вводя две функциональные

переменные v>2, <рз; первый столбец закодируем в виде 00, второй — 01, тре

тий — 10. Отсюда получаем зависимости

У>2(хз, xt, x s)|i = V(5), <?з(хз, xt, r s ) |i = v(3 ).

В результате введения функциональных переменных <pi, tpi, <рз получаем

таблицу Вейча (табл. 2.10), определяющую заданную функцию /(* », гг, • • •, 15 )

через функциональные переменные <fi, tpi, 4>з-

Таблица 2.10

<fii 4>l

0, 1 ,2,4,6,7

0 1

0 0 1

Таблица Вейча (табл. 2.10) определяет внешнюю функцию

ev \ / 1 иа 0, 2, 6,

F(<pu v2,v3) = {0 на х;4; 5’

102

Гл. 2. Математическая логика

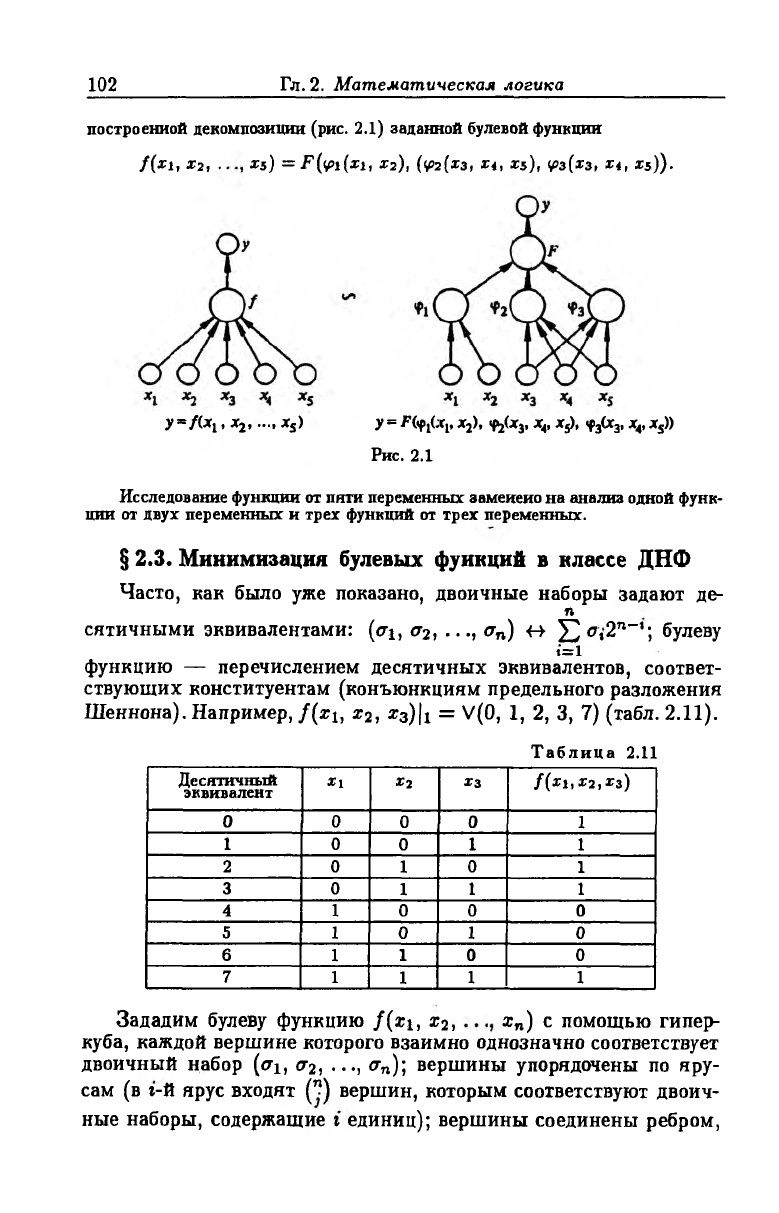
построенной декомпозиции (рис. 2.1) заданной булевой функции

f ( x 1, Х2 , Х5) =F(lfil(xi, Х2), (<р2 (хз, X t, X S ), <рз(хз, Xi, x sj).

у » /(* !, Jt2

.......

Jts ) у = F (f jfctj, х2), <^(лг3, Jt4, Jt5), «p3(x3, x4, jts))

Рис. 2.1

Исследование функции от пяти переменных замеиеио на анализ одной функ

ции от двух переменных и трех функций от трех переменных.

§ 2.3. Минимизация булевых функций в классе ДНФ

Часто, как было уже показано, двоичные наборы задают де-

сятичными эквивалентами: (<7i, а2, •••■> <*п) <-»• ]С°»2П_'; булеву

t'=i

функцию — перечислением десятичных эквивалентов, соответ

ствующих конституентам (конъюнкциям предельного разложения

Шеннона). Например, f(xi, х2, x3)h = V(0, 1, 2, 3, 7) (табл. 2.11).

Таблица 2.11

Десятичный

эквивалент

Х\

х2 *3

f(l l , X 2,Х3)

0 0

1 0

0 1 1

2 0

3 0

1 1

4 1 0 0 0

1 0 1 0

1 0 0

7 1

1 1

Зададим булеву функцию f(xi, х2, х„) с помощью гипер

куба, каждой вершине которого взаимно однозначно соответствует

двоичный набор (<7i, а2, ..., <тп); вершины упорядочены по яру

сам (в г-й ярус входят (”) вершин, которым соответствуют двоич

ные наборы, содержащие г единиц); вершины соединены ребром,

§2.3. Минимизация булевых функций в классе ДНФ

103

если соответствующие им двоичные наборы отличаются в одном и

только одном разряде.

Вершины, в которых /(* i, х2, ..., хп) = 1 и которые образуют

гиперкуб, порождают единичный интервал этой функции. Единич

ный интервал /„ булевой функции / называется максимальным,

если не найдется единичный интервал Д, строго включающий

В данном примере единичными интервалами являются множе

ства вершин {0}, {1}, {2}, {3}, {7}, {0, 1}, {0, 2}, {1, 3}, {2, 3},

{3, 7}, {0, 1, 2, 3}; максимальными интервалами — {0, 1, 2, 3},

{3, 7}.

Конъюнкция, соответствующая максимальному единичному

интервалу функции /, называется простой импликантой этой

функции: {0, 1,2,3} {3, 7} «

Будем задавать единичный интервал перечислением вершин,

а также с помощью последовательности символов 0, 1, —, где про

черк означает отсутствие в конъюнкции соответствующей перемен-

ной: {0, 1, 2, 3} <-► 0 -, {3, 7} Н- -11.

Дизъюнкция всех простых импликант булевой функции назы

вается сокращенной ДНФ этой функции.

Переход от совершенной ДНФ к сокращенной однозначен и осу

ществляется с помощью попарного сравнения конституент сосед

них ярусов (номера которых отличаются на единицу).

Пример 2.4. Найдем сокращенную ДНФ булевой функции f(xi, х2, хз,

ц ) (рис. 2.2): /(* !, 12, хз, *4)|i = V(0, 1, 2, 3, 6, 7, 8, 10, 12, 14, 15).

Сравнивая точку 0000 нулевого яруса с точками первого яруса 1000, 0010 и

0001, получаем три ребра, —ООО, 00—0 и ООО- соответственно, которые образуют

104

Гл. 2. Математическая логика

нулевой реберный ярус. Действуя аналогично, получаем:

ребра первого яруса

{8, 12} -> 1-00, {8, 10} -> 10-0, {2, 10} -> -010,

{ 2, 6 } - > 0 - 10, { 2, 3} т+ 001— , { 1, 3} - > 00- 1;

ребра второго яруса

{ 12, 14} -> 11- 0 , { 10, 14} - > 1 - 10, {6, 14} -> - 110,

{6, 7} - > 011- , { 3, 7} - > 0 - 11;

ребра третьего яруса

{ 14, 15} -> 111- , { 7, 15} -> - 111.

Все точки включены в ребра, следовательно, ни одна из точек не образует

максимальный интервал.

Сравнивая ребра соседних ярусов, формируем ярусы граней:

нулевой —

{-000, -010} = {00-0, 10-0} -> -0-0,

{000-, 001-} = {00-0, 00-1} -> 00—-;

первый ■

{1-00, 1-10} = {10-0, 11-0} -> 1

---

{-010, -110} = {0-10, 1 — 10} —>

----10,

{0-10, 0-11} = {001—, 011-} -> 0— 1—;

второй —

{011—, 111-} = {-001, -111} -> - 1 1 - .

Все шестнадцать ребер включены в грани, следовательно, ни одна из них не

образует максимальный интервал.

Сравнивая грани соседних ярусов, замечаем, что ни одна из пар сравнивае

мых граней ие образует куб. Следовательно, все шесть граней являются мак

симальными интервалами, и соответствующие им конъюнкции представляют

собой простые импликанты. В результате сокращенная ДНФ рассматриваемой

булевой функции имеет вид

/ ( * 1 , *2 , хз, *« ) = x2Xi V Х1Х2 V XiXi V Г3Х4 V 1 1 Г 3 V Х2Х3,

и сложность ее 12.

Сложность уменьшится до 6 в результате определения минимального покры

тия столбцов строками в импликантной таблице (табл. 2.12)

Таблица 2.12

Простые

импликаиты

Коиституенты

0 1 2 3

6 7

8 10 12 14 15

1 1

00—

1 1

-----

Ф Ф Ф Ф

-----

1 1

0 - 1 -

1 1 1

-1 1-

§ 2.3. Минимизация булевых функций в классе ДНФ

105

В столбцах, соответствующих конституеитам 1, 15 и 15, находится одна 1,

следовательно, соответствующие строки {00

-----

, 1

-----

0, —11—} образуют ядро

покрытия. Это ядро является покрытием столбцов строками, следовательно, оно

минимальное (рис. 2.2):

/ (Г 1, Х2, Х3, Г<) = XlX2 V XlXi V Х2Х3.

Большое значение имеют слабоопределенные булевы функции

/(х 1, z2, . . хп) которые обладают следующими свойствами:

1) число переменных п велико;

2) мощность объединения единичной V\ и нулевой Vo областей

намного меньше, чем 2П, где единичную и нулевую области обра

зуют вершины, в которых функция равна соответственно 1 и 0;

3) единичная и нулевая области задаются соответствующими

интервалами.

Множество вершин гиперкуба, на которых функция равна 0 и

которые образуют гиперкуб, называется нулевым интервалом. Со

кращенную ДНФ слабоопределенных функций строят с помощью

таблицы различий.

Таблицей различий называется двумерная таблица размера

п X |Vo|, каждой строке которой взаимно однозначно соответствует

разряд рассматриваемого единичного интервала, столбцу — нуле

вой интервал, а на пересечении i-й строки с j -ы столбцом нахо

дится результат операции:

0 ф 0 = 0, 1®0=1, -® 0 = 0,

001 = 1, 101 = 0, -01 = 0,

00 — = 0, 1 0 -= 0, — 0 — = о,

причем в качестве первого аргумента берется значение г-го разряда

единичного интервала, в качестве второго — значение i-го разряда

нулевого интервала, соответствующего j-му столбцу.

Выделение максимальных интервалов сводится к покрытию

столбцов строками таблицы различий. В самом деле, максималь

ные интервалы в слабоопределенных функциях состоят из вер

шин единичной и неопределенной областей. Единица в клетке

(г, j) таблицы различий показывает, что если оставить г-й раз

ряд в конъюнкции, то j-й нулевой интервал не входит в гипер

куб, соответствующий этой конъюнкции. Следовательно, покры

тие столбцов строками порождает максимальный интервал полно

стью определенной булевой функции f(x 1, z2, ..., zn), единичная

и нулевая области которой включают соответственно единичную и

нулевую области заданной функции f(x 1, х2, ..., хп). Функция

/(xj, х2,..., хп) называется мажорирующей функцию /(®i, х2,...

• ■ •> *n), 7{хI, х2, • • •, *п) Э f(xi, х2, ..., х„).

Пример 2.5. Найдем минимальную ДНФ булевой функции

f, v _ / 1 иа интервалах 0—0—0—0, 11—0—01, 0— 001—,

Д П , Х2, ..., х7) - { о иа „„тервалах Ю-0-01, 00

-----

10—, 1 1 0 1 -0 -

106

Гл. 2. Математическая логика

или функции, заданной с помощью десятичных эквивалентов минимальных и

максимальных элементов соответствующих интервалов, которые получаются в

результате подстановки нулевого (00.. .0) и единичного (11.. .1) кода вместо про

черков:

. f 1 на интервалах [0, 42], [97, 117], [2, 51],

12’ \ 0 на интервалах [65, 85], [4, 29], [104, 109].

Выделим множество максимальных интервалов { /м ак с} , содержащих еди

ничный интервал [0, 42] по таблице различий (табл. 2.13), у которой строки

идентифицированы буквами а, Ь, с, d, е, д, h.

Таблица 2.13

Единичный

интервал

Нулевые интервалы

[65,85] [4,29]

[104,109]

1 0

—

0 0

—

0 0

е 0 0

1 0

h 0 1

Используя метод Петрика, найдем все покрытия этой таблицы (aVh)ea — ае.

Имеем одно покрытие, соответствующее максимальному интервалу 0

-------

0— Э

D [0, 59], которому соответствует простая импликанта xiis.

Аналогично находим множества максимальных интервалов, содержащих

остальные единичные интервалы:

{/ м « е D [97, 117]} = {[32, 119]} <-> Xix4,

{/м « с Э [2, 51]} = {[0, 59], [2, 123]} t * х&х6.

В результате получена сокращенная ДНФ булевой функции f(xi, х-2, ..., Г7),

являющейся уже полностью определенной. Единичная область И функции / со

держит единичную область Vi функция /:

Vi Э Vi, нулевая область Vo функции / —

нулевую область V0 функции /: Vo D Vo\

f{x 1, Х2, ■ . Х7) = XiX5 V г 2х4 V xsxe.

Выделение максимальных ин

тервалов, построение сокращенной

ДНФ функции / — первый этап ми

нимизации в классе ДНФ, при этом

нулевой столбец в таблице разли

чий указывает на противоречивость

заданной функции. Вторым этапом

является переход от сокращенной

ДНФ^функции / к тупиковой ДНФ

этой функции (рис. 2.3). Функция / мажорирует заданную функ

цию /, / Э /.

ДНФ функции

/(*1. *2

.....

х„)

Покрытие таблицы различий

Сокращенна!

ДНФ функции

/<>1. лг2. .... V

Покрытие импликаитной таблицы

7 5 ‘Ъ

Тупиковые ДНФ функции

fix 1. *2

.....

Рис. 2.3

§2.3. Минимизация булевых функций в классе ДНФ

107

Тупиковой ДНФ булевой функции f(x\, х2, •. ■, хп) называется

ДНФ, не определяющая функцию / с точностью до неопределенной

области при вычеркивании хотя бы одного произвольного первич

ного терма ха'. Тупиковая ДНФ булевой функции получается в

результате покрытия столбцов строками импликантной таблицы

(двумерной таблицы, каждой строке которой взаимно однозначно

соответствует максимальный интервал, столбцу — единичный ин

тервал, а на пересечении г-й строки с j-u столбцом находится 1,

если j -й единичный интервал входит в г-й максимальный интер

вал, в противном случае на пересечении находится 0).

Построим для рассматриваемого примера импликантную таблицу (табл. 2.14).

Таблица 2.14

Максимальные единичные

интервалы функции /

Единичные интервалы функции /

[0,42]

[95,117]

[2,51]

[0,59]

[32,119] . 0 1 0

[2,123]

0 1

Таблица имеет одно покрытие, его образуют первая и вторая строки. Это

покрытие порождает тупиковую ДНФ функции

/ ( * 1, * 2, • • •, *7) = XlXs V X2Xt.

Теоретически число тупиковых ДНФ булевой функции f(x 1,

*2) • • •) ®п) при п -¥ ос растет как число всех различных буле

вых функций от п переменных 22". Практически же количество

тупиковых ДНФ увеличивается значительно медленнее, чем 22",

из-за большого количества недоопределенных вершин гиперкуба.

Перебор всех тупиковых ДНФ булевой функции определяет выбор

минимальной ДНФ этой функции.

В рассматриваемом примере тупиковая ДНФ одна; следова

тельно, она является минимальной ДНФ функции f(x\, х2, ...

. . £ 7). ^

/(а, Ь, с, d) ~ad.V be,

где а = xi, b = х2, с = х±, d = Х5. При таком доопределении

функция зависит от четырех переменных.

Булева функция, полученная из функции f(x 1, х2,..., хп) фик

сированием г-й переменной, г 6 {1, 2, . . п}, как уже было опреде

лено, называется остаточной. Если г,- = 1, то остаточная функ

ция называется единичной, если г,' = 0 — нулевой.

Булева функция f(x 1, х2, ..., хп) несущественно зависит от

г-й переменной, если ее остаточные функции по этой переменной

равны.

108

Гл. 2. Математическая логика

§ 2.4. Полнота. Построение

суперпозиций булевых функций

Любое сложное высказывание можно представить в виде вы

ражения, в которое входят простые высказывания (переменные)

Х{, операции дизъюнкции, конъюнкции, отрицания и, быть может,

скобки. Рассмотрим, каким свойствам должны удовлетворять опе

рации, с помощью которых можно выражать любое сложное вы

сказывание.

Будем моделировать конъюнкцию и дизъюнкцию соответст

венно последовательным и параллельным соединением ключевых

элементов (для определенности — полупроводниковых), отрица

ние — включением нагрузки в коллекторную цепь транзистора.

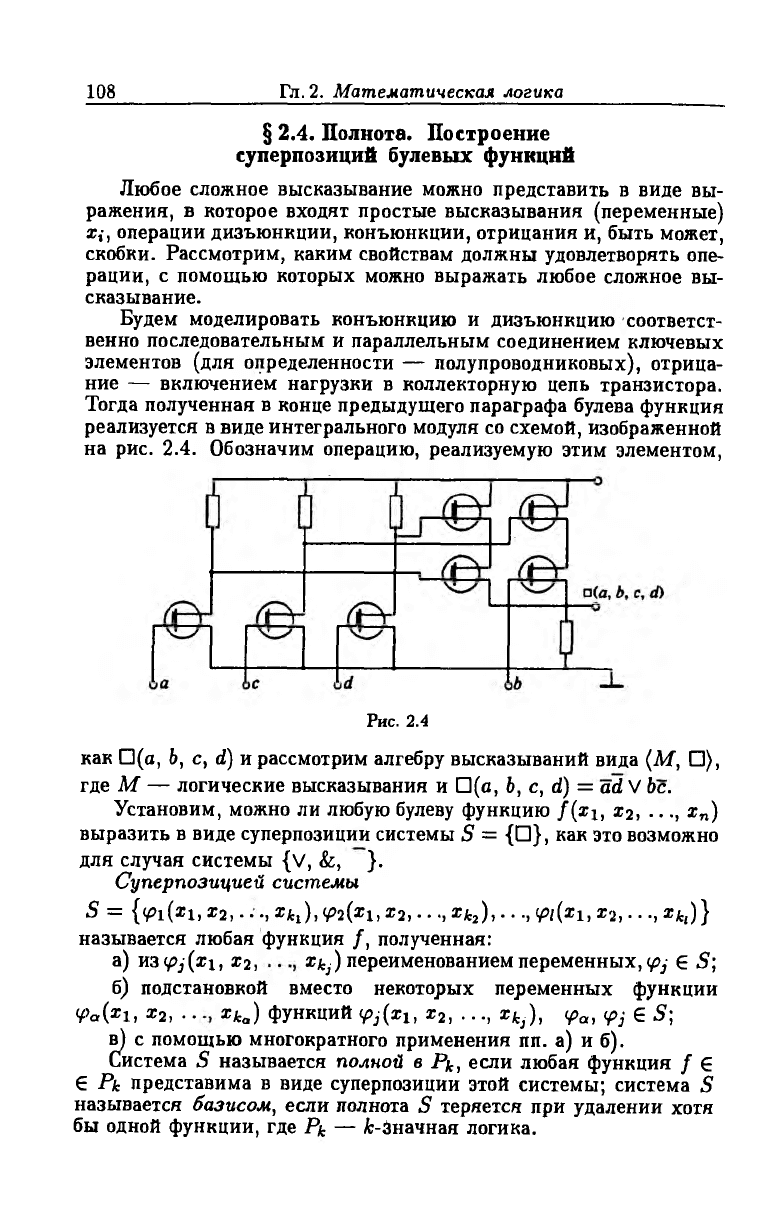
Тогда полученная в конце предыдущего параграфа булева функция

реализуется в виде интегрального модуля со схемой, изображенной

на рис. 2.4. Обозначим операцию, реализуемую этим элементом,

Рис. 2.4

как П(а, Ь, с, d) и рассмотрим алгебру высказываний вида (М, □),

где М — логические высказывания и Ш(а, Ь, с, d) = ad V be.

Установим, можно ли любую булеву функцию / ( * х , Х2, . . . , хп)

выразить в виде суперпозиции системы S = {□}, как это возможно

для случая системы {V , &, }.

Суперпозицией системы

S = { v > l(z i, х2, • • •, Xkt), Ы хъ *2, • • •, Хк2 ), • • ., < p l ( x i,X2, ■ ■ ; zjfc,)}

называется любая функция /, полученная:

а) из^-(х1, Х2, Xkj) переименованием переменных, <pj 6 S ;

б) подстановкой вместо некоторых переменных функции

¥> а(*1, Х2 , . . Хка) функций tpj(zi, х2 , . . ., X kj), <fia , <pj в S ]

в) с помощью многократного применения пп. а) и б).

Система S называется полной в Рк, если любая функция / 6

6 Рк представима в виде суперпозиции этой системы; система S

называется базисом, если полнота S теряется при удалении хотя

бы одной функции, где Рк — к-bначная логика.

§ 2.4. Полнота. Построение суперпозиций булевых функций 109

Выразим дизъюнкцию и отрицание через П(а, Ь, с, d); тогда

согласно разложению Шеннона и закону де Моргана любую булеву

функцию f(x\, х2, ..., хп) можно выразить через S = {□}:

а = □(«, а, а, а);

а V /3 = cm V /3/3 = □(«, /3, /3, а) =

= □ (□(<*, а, а, а), /3, □(/?, /3, /3, /3), Ш(а, а, а, а)).

В общем случае для установления полноты системы S буле

вых функций /, (S в Р2) используют критерий полноты Поста-

Яблонского.

Определим предварительно пять классов булевых функций.

Классом Ко булевых функций fi(xi, х2, ..., хп), сохраняющих

константу 0, называется множество функций вида

{/»'(* 1) х2) ■ • •) хп)/ /«(0) 0, ..., 0) = 0}.

Классом К \ булевых функций х2, хп), сохраняющих

константу 1, называется множество функций вида

Ш * 1- х2, • ■ •, хп)/ fi(l, 1, . . 1) = 1 }.

На примере системы S — {□ } рассмотрим тесты распознавания функций,

обладающих этими свойствами:

□(а, Ь, с, tf) = а5 V Ьс,

□(О, 0, 0, 0) = Об V00 = 1 V0 = 1, D(o, Ь, с, d) i Ко,

□(1, 1, 1, 1) = I! V II = О V 0 = 0, 0(0 , Ь, с, d) i Ki.

Классом К л линейных булевых функций /,-(*!, х2, ..., хп) на

зывается множество функций вида

) х 2) • • ч хп)/ ft(x 1) х 2) • • •) хп) = с0 Ф ^ ] cixi J )

где ® — знак операции сложения по модулю 2: 000 = 0, 0® 1 = 1,

1Ф 0 = 1, 1® 1 = 0.

Установим, является ли булева функция D (a, Ь, с, d) линейной. Предполо

жим, что она линейная и, следовательно, представима в виде

Определим коэффициент со: 0 (0 , 0, 0, 0) = 1, но по предположению 0 (0 , О,

О, 0) = со. Следовательно, со = 1.

Аналогично определим коэффициенты са, сь, сс, сл, фиксируя соответствен

но наборы 1000, 0100, 0010, 0001. Имеем:

□(1, О, О, 0)=T -0V 0-0 = 0V0 = 0,

1 0 Са ■ 1 0 СЬ ■ 0 0 Сс • 0 0 Cd ■ 0 = 1 0 Са, 1 0 Со = 0 , Са — 1’,

□(о, 1, о, o)=oovi-o = ivi = i,

101-00 сь -10 сс -00 Cd -0=10 сь, 10сь = 1, сь = 0;

110

Гл. 2. Математическая логика

□(О, 0, 1, 0) =0-0 V0-1 = 1 V0 = 1,

d(0, О, о, i)=o Tvo o = ovo = o,

Подставляя значения коэффициентов в приведенное выше выражение, получаем

□(а, Ь, с, d) = 1 ® а ф d.

Это равенство в каждой из остальных 11 точек не сохраняется. Действи

тельно, в точке (1, 1, 1, 1) имеем

□ (1, 1, 1, 1) = T l V 1 0 = 0 V 0 = 0,

Следовательно, сделанное предположение является неверным.

Функция 0(а, Ь, с, d) нелинейная: □(а, Ь, с, d) $ Кж.

Классом самодвойственных булевых функций fi(x\, х2, ...

..., хп) называется множество булевых функций вида

Х2, . . Хп)/ /(*!, х2, . . Хп) = fi{xu х2, . . яп)}.

Рассмотрим свойство самодвойственности булевой функции D(a, Ь, с, d). По

строим таблицу значений 2 х 2" (п = 4), в которой в первой строке распола

гаются десятичные эквиваленты, соответствующие наборам

X — (а, Ь, с, d), во

второй — значения функции f(X) — 0(a , Ь, с, d), которые соответствуют этим

наборам.

Таблица 2.15

2 3 4 5

7 8

9 10

12 13

14 15

/(*)

0 1 0

0 0 1

Функция самодвойственная, если на любой паре противопо

ложных наборов (наборов, сумма десятичных эквивалентов кото

рых равна 2п —1) функция принимает противоположные значения.

Функция Ш(а, Ь, с, d) ие является самодвойственной: D(7) = D(8).

Классом К м монотонных булевых функций /,-(*!, х2, ..., хп)

называется множество булевых функций вида

{/•(* 1, Х2, . .., хп)/ (aj, СТ2, ..., О > (<Т1, а2, ..., ап)

(а* > * = 1, 2, ..., п) ->•

-> /К *. а2, • • О > /(*1, *2, • • •, *п)}-

Для тестирования функции 0(а , Ь, с, d) на монотонность построим гиперкуб

и проанализируем распределение в нем значений этой функции (рис. 2.5).

Если найдется хотя бы одно ребро, концам которого сопоставлены двоичные

наборы (<rl,<rj,..., О и(<Г1,<Г2,...,огп) вида (<r*,orJ,..., <т^) > (<гь <т2,..., <т„),