Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика
Подождите немного. Документ загружается.


§1.8. Компьютерные арифметики
71
случае сумма тетрад принимает следующий вид:
х 4- у < 10,
Т(*) + Т(у) = ® + 3 + у + 3 = ж + у + 6,
Т(х + у) = х + у + 3,
следовательно, поправка равна —3 (в обратном коде — 1100, в до
полнительном — 1Ю1), т. е.
Т(х + у)-(Т(*)+Т(у)) = -3;
X + у > 10,
Т(х) + Т(у) = ж + 3 + у + 3 = а: + у + 6,
Т(х + у) = ж + у-10 + 16 + 3 = а: + у + 9,
следовательно, поправка равна +3, т. е.
Т(* + у)-(Т(*) + Г(у)) = 3.
Таким образом, получаем
+ у) + 3, ж 4- у < Ю,
4- у) - 3, * 4- У > Ю.
Приведем пример суммирования чисел —471 и 607 с использо
ванием дополнительного кода:
—471 — 1000 0101 1100 кодирование
+607 — 1001 ООН 1010
+ 10001 1001 0110 первое суммирование, отбрасывание
0001 1001 0110 переноса из левого разряда
0011 1101 0011 поправка
т(*)+т(»)={£{*:
136 — 0100 0110 1001 получение результата после поправок
Кодирование с избытком 3 не обладает свойством весомозна
чимо сти. Единственным кодированием, которое обладает всеми
пятью свойствами, является кодирование Айкена—Эмери. Это
кодирование с весами (2, 4, 2, 1).
Вычислим эти коды при pi > 0.
Для кодирования 1 необходимо, чтобы один из весов был равен
1. Для определенности будем считать, что р4 = 1, тогда pi + р2 +
+Рз = 8. Возможные комбинации весов (pi, р2, Рз) с точностью
до их перестановки:
(1,1,6), (2,1,5), (2,2,4), (2,3,3), (1,3,4).
В системе с весами (6,1,1,1):
0 — 0000, 1 — 0001, 2 — 0011, 3 — 0111, 4 —
5 — , 6 — 1000, 7 — 1001, 8 — 1011, 9 — 1111.

72
Гл. 1. Основы многосортных множеств
Для случая (1,1,6) нарушается первое требование Рутисхаузера:
для цифр 4 и 5 отсутствуют соответствующие тетрады.
В системе с весами (5,2,1,1):
0 — 0000, 1 — 0001, 2 — 0100, 3 — 0101, 4 — 0111,
5 — 1000, 6 — 1010, 7 — 1011, 8 — 1110, 9 — 1111;
не выполняется требование четности для цифр 4 и 5.
В системе с весами (3,3,2,1):
0 — 0000, 1 — 0001, 2 — 0010, 3 — 0011, 4 — 0101,
5 — 1010, 6 — 1100, 7 — 1101, 8 — 1110, 9 — 1111;
не выполняется требование четности для цифр 4 и 5.
В системе с весами (4,3,1,1):
0 — 0000, 1 — 0001, 2 — 0011, 3 — 0100, 4 — 0110,
5 — 1001, 6 — 1011, 7 — 1100, 8 — 1110, 9 — 1111;
не выполняется требование четности цифр для цифр 2, 3, 6, 7.
В системе с весами (2,4,2,1):
0 — 0000, 1 — 0001, 2 — 0010, 3 — 0011, 4 — 0100,
5 — 1011, 6 — 1100, 7 — 1101, 8 — 1110, 9 — 1111;
все пять требований выполнены, соответствующая арифметика
является совершенной и называется в честь авторов — арифме
тикой Айкена—Эмери. Анализируя коды, замечаем, что
Для определения правил суммирования тетрад необходимо рас
смотреть следующие случаи:
1) х < 5, у < 5, х -f у < 5; Т(х) 4- Т{у) = х 4- у, Т(х 4- у) =
= х + у, Д = Т(х 4- у) - (Т(х) 4- Т(у)), Д = 0;
2) * < 5, у < 5, 5 < * 4- у < Ю; Т(х) 4- Т(у) = ж 4- у,
Т(х 4- у) = ж 4- У + 6, Д = 6;
3) х < 5, у > 5, 5 < х 4- у < Ю; Т(х) 4- Т(у) = х 4- (у 4- 6),
Т(х 4- у) = * 4- У 4- 6, Д = 0;
4) х < 5, у > 5, 10 < х 4- у < 15; Т(х) 4- Т(у) = х 4- (у 4- 6),
Т(х 4- у) + 6 (6 из-за переноса) ?= ж 4- у 4- 6, Д = 0;
5) я > 5, у > 5, 10 < *4-у < 15; Т(х)+Т{у) = {х4-6)4-{у 4-6),
Т(х 4- у) 4- 6 = (х 4- у) 4- 6, Д = -6;
6) х > 5, у > 5, х 4- у > 15; Т{х) + Т(у) - {х 4- 6) 4- (у 4- 6),
Т{х + у) 4- 6 = (х 4- у 4- 6) 4- 6, Д = 0.
Таким образом, при суммировании *4-у в коде Айкена—Эмери
необходима поправка 4-6 в тетрадах, когда х < 5, у < 5, 5 < ж+у <
< 10, и поправка -6 , когда х > 5, у > 5, 10 < х 4- у < 15.

§ 1.8. Компьютерные арифметики
73
Просуммируем в этом коде рассмотренную выше пару чисел
471 и 607, используя при этом дополнительный код. Имеем
-471 — 1000 0101 1100
+607 — 1001 0011 1010
10111
0011
1100
0111
+ 1010
0011
+ 0000
1100
+ 0000
1
1 1
случай 5)
случай 1)
случай 6)
+136 — 0001 ООН 1100
Производительность процессора существенно повышается, ес
ли обработать каждый разряд независимо от других. Эту возмож
ность предоставляет код в остатках.
Системой счисления, позволяющей производить вычисления в
каждом разряде независимо от результатов, полученных в других
разрядах, является код в остатках. Множеством модулей кода
в остатках называется множество S взаимно простых натураль
ных чисел: qi, Я2, . . qs-
Обозначим через res (x/qi) остаток от целочисленного деления
х на Кодом в остатках числа х по множеству модулей qi,
<72, • • -, Яз называется выражение вида
х х х
res — res —... res —.
Я\ Я2 Я*
Если res(a;/<fr) = а и res (x/qi) = /3, то х = nяi + а и у =
= mqi + /3.
Проведем алгебраическое суммирование последних двух ра
венств. В результате получаем х + у — (п + т) • я< + (<* + ($)•
Теперь перемножим соответственно правые и левые части исход
ных равенств:
х • у — (т • п ■ qi + п • (3 + т • а) • qi + а • /3.
Если а + (3 и а • (3 меньше д,-, то можно утверждать, что при
Суммировании и умножении двух чисел их остатки от деления qi
также складываются или перемножаются. Если же а + /3 и а • /3
больше qi, то, разделив их на д, и определив целое частное, полу
чим, что утверждение о суммировании и перемножении остатков
совпадает с ранее высказанным, если считать, что после выполне
ния этих операций происходит деление на модуль данного разряда
И выделение истинного остатка. Подобная операция может иметь
место для каждого разряда независимо от других, поэтому код в
остатках позволяет суммировать и перемножать поразрядно, что
позволяет увеличить скорость выполнения операций ЭВМ.
Пусть, например, имеется система из трех модулей: 7, 8, 9.
Тогда коды в остатках для чисел а: = 11 и у = 6 имеют соответ
ственно виды 432 и 666. Просуммируем и перемножим поразрядно
74
Гл. 1. Основы многосортных множеств
коды х и у; тогда получаем 10 9 8 и 24 18 12. После деления
в каждом разряде результата на модуль этого разряда и выделе
ния истинного остатка получим соответственно 318 и 323. Сумма
и произведение ж и у, равные 17 и 66, имеют коды в остатках
318 и 323.
Для получения взаимно однозначного представления чисел в
коде в остатках следует учитывать, что если произведение всех
модулей qi, используемых для кодирования, есть N , то взаимно
однозначно в коде в остатках с этими модулями можно кодировать
лишь N различных чисел (от 0 до N - 1, от N до 2N - 1 и т. д.).
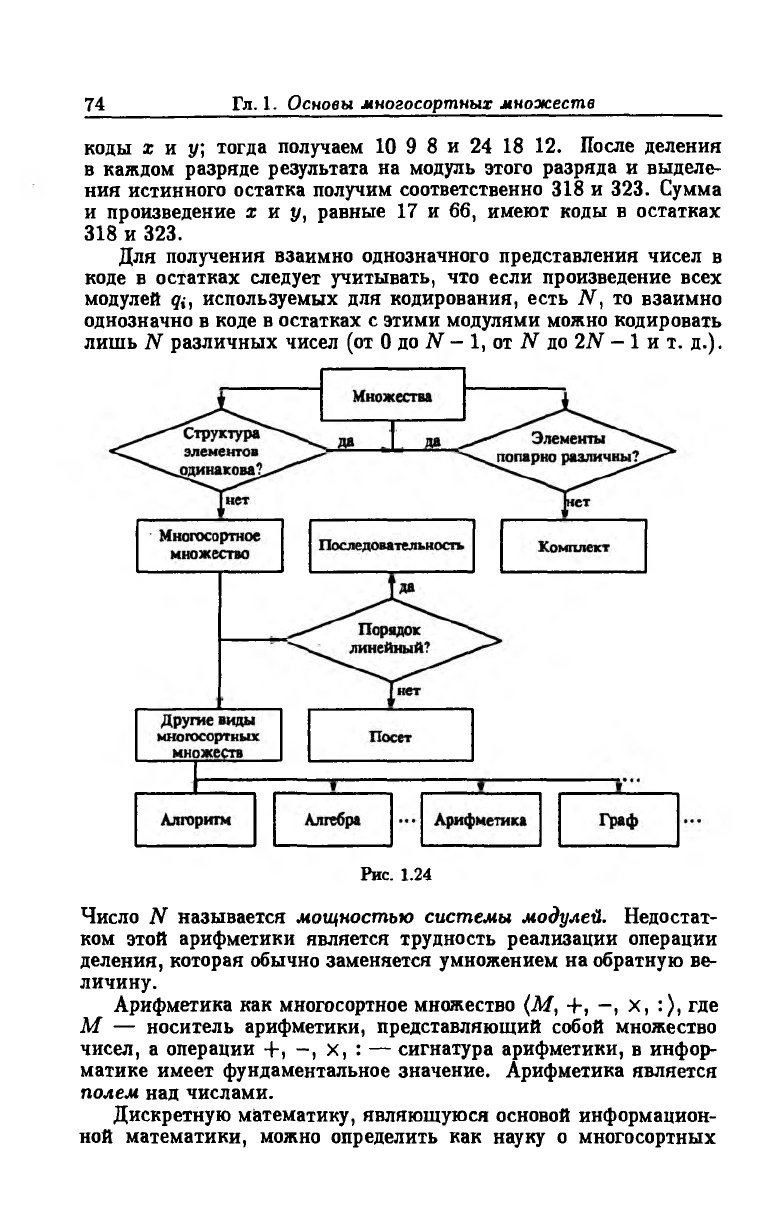
Рис. 1.24
Число N называется мощностью системы модулей. Недостат
ком этой арифметики является трудность реализации операции
деления, которая обычно заменяется умножением на обратную ве
личину.
Арифметика как многосортное множество (М, -f, - , х, :), где
М — носитель арифметики, представляющий собой множество
чисел, а операции +, - , х, : — сигнатура арифметики, в инфор
матике имеет фундаментальное значение. Арифметика является
полем над числами.
Дискретную математику, являющуюся основой информацион
ной математики, можно определить как науку о многосортных

§1.9. Нечеткие подмножества
75
множествах (совокупностях)
<м, т , { ял , {о^1» ,
где М — множество, в котором заданы операции {О,}; {Лу} —
отношения и — кооперации, определяющие соответственно
законы композиции, свойства и законы декомпозиции.
Вложение друг в друга основных понятий дискретной матема
тики показано на рис. 1.24, где посетом названо частично упоря
доченное множество (partially order set), комплектом — множе
ство, в котором найдутся хотя бы два одинаковых элемента.
§ 1.9. Нечеткие подмножества
Расширим понятие подмножества, введя свойство нечеткости
(размытости).
Принадлежность элемента х подмножеству А:
х £ А, А с М,
будем задавать с помощью характеристической функции
( \ / 1) еспи х € А,
— \о в противном случае.
Представим теперь, что характеристическая функция может
принимать любое значение в интервале [0, 1]. В соответствии с
этим элемент х множества М может не принадлежать А (ца(х) —
= 0), может быть элементом А в небольшой степени (цл близко к
0) или, наконец, может быть элементом А (уд = 1). Таким обра
зом, понятие принадлежности получает интересное обобщение при
решении практических задач.
Математический объект, определяемый выражением
А ={{Х1 (0.2), (*2|0), (х3|0.3), Ы 1 ), (*5|0.8)},
где Х{ — элемент универсального множества М, а число после
вертикальной черты дает значение характеристической функции
на этом элементе, будем называть нечетким подмножеством А
множества М и обозначать А С М. При этом нечеткое подмно
жество А: содержит в небольшой степени *i; не содержит х2; со
держит хз в немного большей степени, чем ж2; полностью содер
жит ®4; в значительной мере содержит х$. Таким образом, мы
можем создать математическую структуру, которая позволяет опе
рировать с относительно неполно определенными элементами и
принадлежность которой к данному подмножеству упорядочена. К
таким структурам можно, например, отнести: в заданном мно
жестве людей — некоторое подмножество очень высоких людей;
во множестве основных цветов — нечеткое подмножество темно
зеленых цветов; во множестве решений — нечеткое подмножество

76
Гл.1. Основы многосортных множеств
хороших решений и т. д. Далее мы увидим, как обращаться с та
кими понятиями, которые особенно хорошо подходят к описанию
неточности, присущей моделям искусственного интеллекта.
Дадим строгое определение нечеткого подмножества.
Пусть М — множество и ж — элемент М . Тогда нечеткое
подмножество А множества М определяется как множество упо
рядоченных пар {ж, Ух 6 М , где Ца{х) — характеристи
ческая функция принадлежности, принимающая свои значения на
упорядоченном множестве Р, которая указывает степень или уро
вень принадлежности элемента ж к подмножеству А. Множество
Р будет называться множеством принадлежностей.
Если Р = {0, 1}, то нечеткое подмножество А будет рассма
триваться как не нечеткое”, или “обычное” подмножество. Та
ким образом, понятие нечеткого подмножества связано с понятием
множества и позволяет изучать нестрого определенные понятия,
используя математические структуры.
Рассмотрим несколько примеров:
1) нечеткое подмножество чисел ж, приблизительно равных
данному действительному числу п, где п € R (R — множество
действительных чисел);
2) нечеткое подмножество целых чисел, близких к 0;
3) пусть а — действительное число и ж — небольшое поло
жительное приращение а; тогда числа а + ж образуют нечеткое
подмножество во множестве действительных чисел.
Пусть М — множество, Р — множество принадлежностей, А
и В — два нечетких подмножества М . Будем говорить, что А
содержится в В , если (Vx £ М ) (ца(х) < Цв{х)), и обозначать
А С В.
Строгое включение соответствует случаю, когда по крайней ме
ре одно неравенство строгое, и обозначается А С С В.
Пусть М — множество, Р — множество принадлежностей, А
и В — два нечетких подмножества. Скажем, что А к В равны
тогда и только тогда, когда (Vz € М) (ца(х) = Нв(х)), и будем
обозначать А = В.
Если найдется по крайней мере один такой элемент ж из М,
что равенство Ца{х) = Цв{х) не удовлетворяется, то мы будем
говорить, что А к В не равны, и обозначать АфВ.
Определим операции над нечеткими подмножествами, анало
гичные операциям алгебры Кантора.
Дополнение. Пусть М — множество, Р — [0, 1] — множество
принадлежностей, А и В — два нечетких подмножества; скажем,
что А к В дополняют друг друга: А — В или В — А, если
(Уж € М ) (цА{х) = 1 - Цв(х)). _
Очевидно, что имеет место закон двойного дополнения А — А.
§1.9. Нечеткие подмножества
77
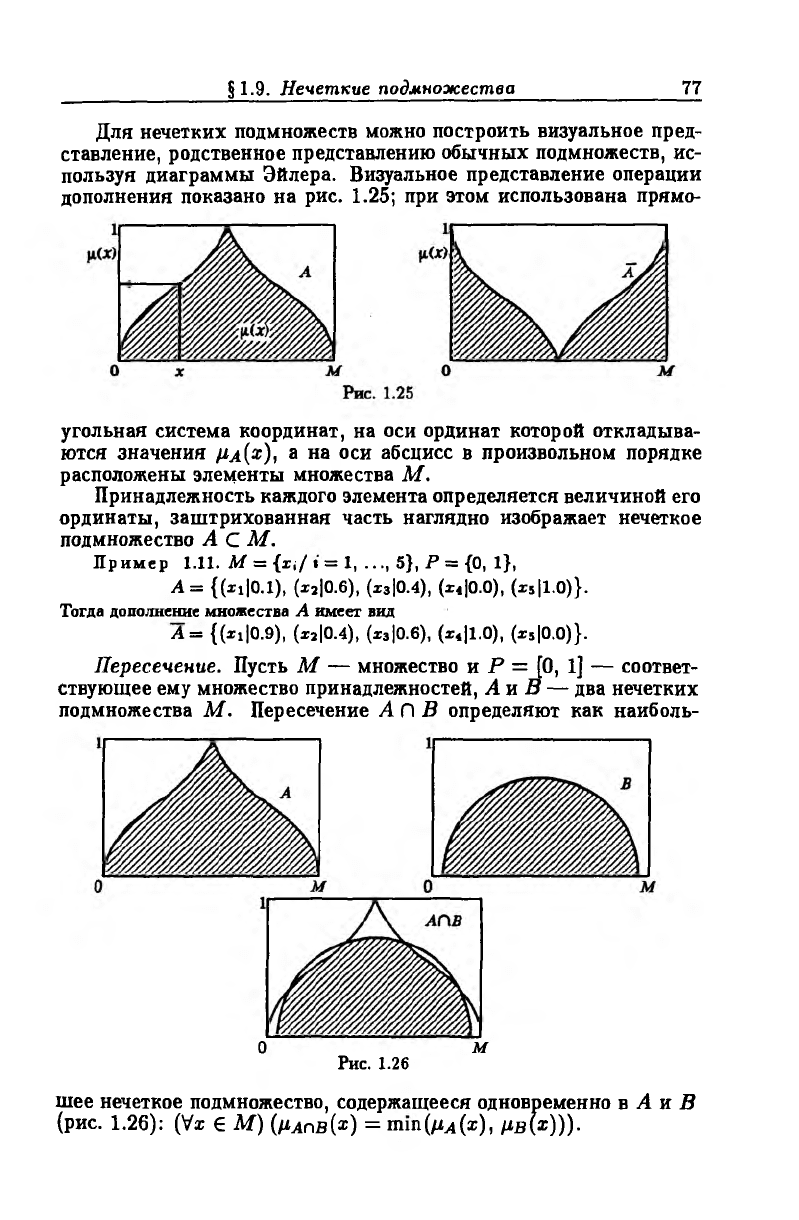
Для нечетких подмножеств можно построить визуальное пред
ставление, родственное представлению обычных подмножеств, ис
пользуя диаграммы Эйлера. Визуальное представление операции
дополнения показано на рис. 1.25; при этом использована прямо
угольная система координат, на оси ординат которой откладыва
ются значения /ла(х), а на оси абсцисс в произвольном порядке
расположены элементы множества М.
Принадлежность каждого элемента определяется величиной его
ординаты, заштрихованная часть наглядно изображает нечеткое
подмножество А С М.
П рим ер 1.11. М = {ц / • = 1, ..., 5}, Р = {0, 1},
А= {(*i|0.1), (*2|0.6), (*з|0.4), (s4|0.0), (*S|1.0)}.
Тогда дополнение множества А имеет вид
А= {(*i|0.9), (zs|0.4), ( i3|0.6), (**|1.0), (*s|0.0)}.
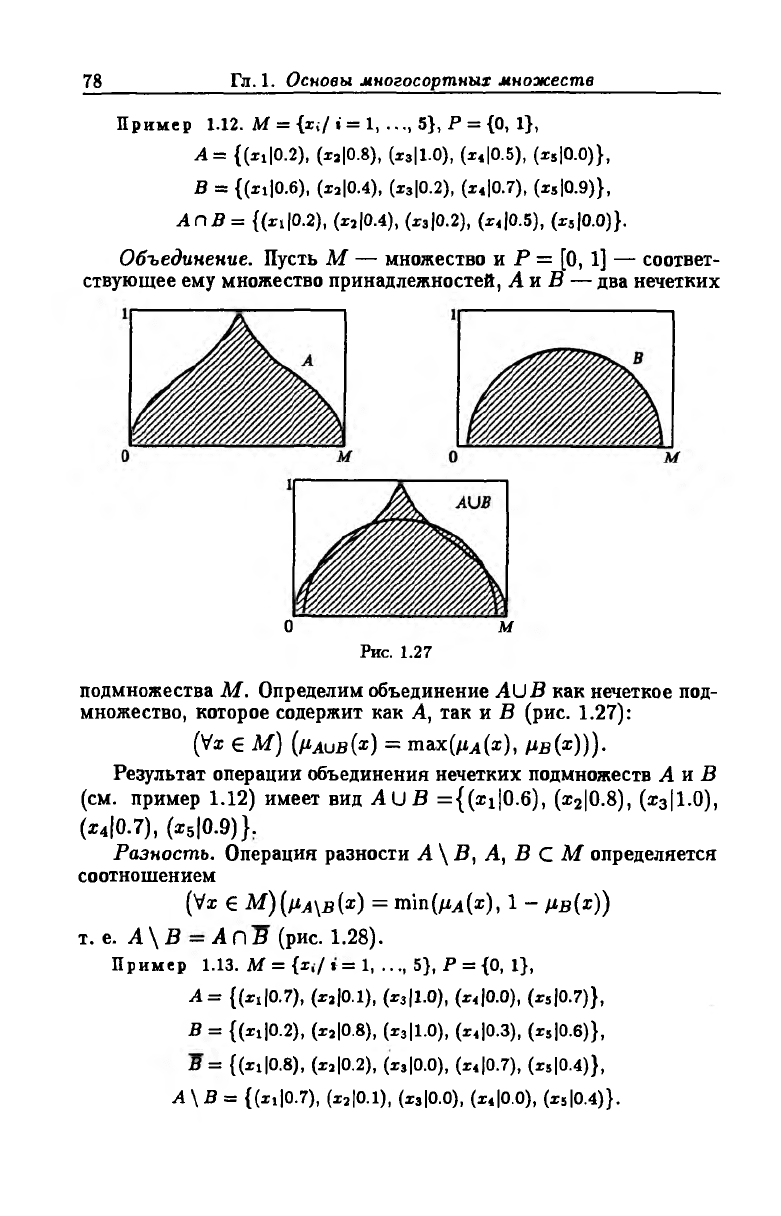
Пересечение. Пусть М — множество и Р = [0, 1] — соответ
ствующее ему множество принадлежностей, А и В — два нечетких
подмножества М . Пересечение АП В определяют как наиболь-
0 м
Рис. 1.26
шее нечеткое подмножество, содержащееся одновременно в А и В
(рис. 1.26): (Va; € М ) (/i^nfifc) = тт(цА(х), рв(х))).
78
Гл. 1. Основы многосортных множеств
Пример 1.12. М = {xi/ « '= 1 ,..., 5}, Р = {О, 1},
А= {(*i|0.2), (*а|0.8), (*з|1.0), (*«|0.5), (*S|0.0)},
В = {(ц|0.6), (ij|0.4), (*,|0.2), (*«|0.7), (*s|0.9)},
АПВ = {(*х|0.2), (*а|0.4), (*»|0.2), (*<10.5), (г8|0.0)}.
Объединение. Пусть М — множество и Р = [0, 1] — соответ
ствующее ему множество принадлежностей, А и В — два нечетких
О м
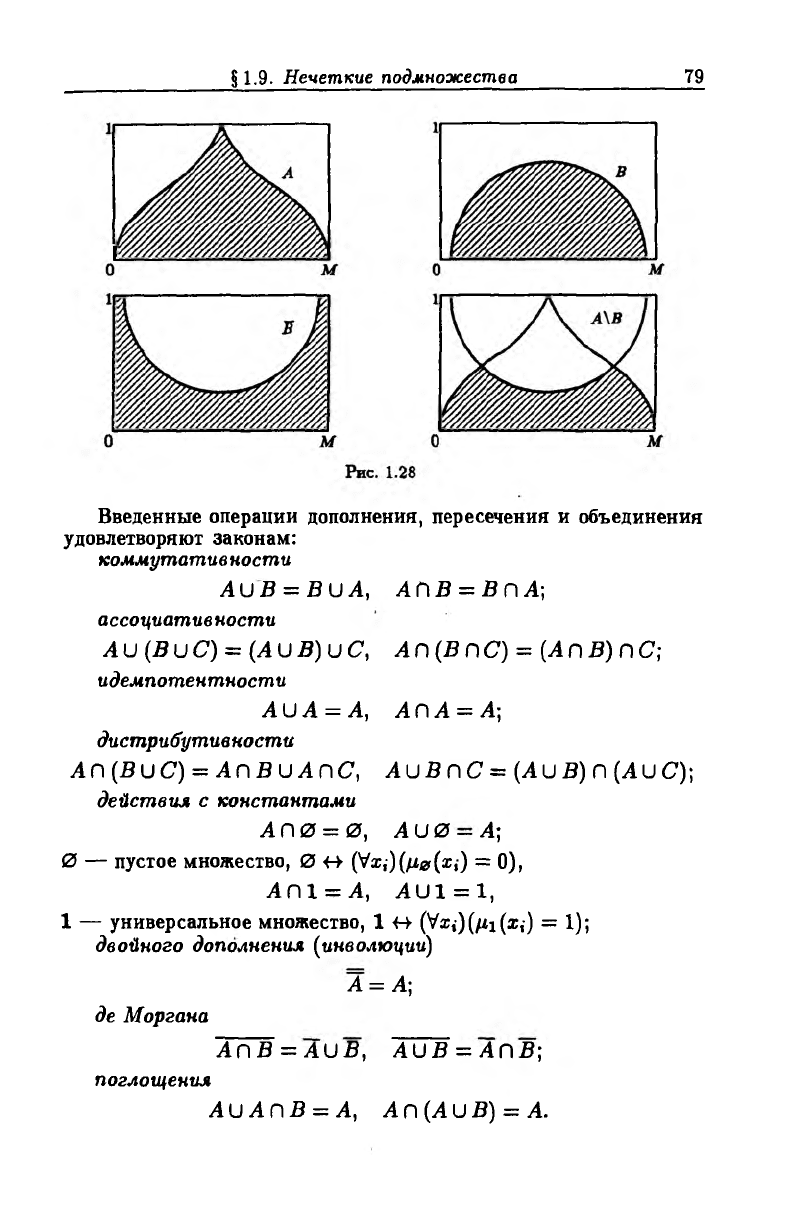
Рис. 1.27
подмножества М . Определим объединение AUB как нечеткое под
множество, которое содержит как А, так и В (рис. 1.27):
(V® £ М ) (^Аив(х) = тах(/и(*), ц в(*)))•
Результат операции объединения нечетких подмножеств А и В
(см. пример 1.12) имеет вид AU В ={(агх|0.6), (ж2|0.8), (*3|1.0),
(г4|0.7), (х5|0.9)}.
Разность. Операция разности А\В, А, В С М определяется
соотношением
(V* € М)(цА\в {х) = minf/uH, 1 - Цв(х))
т. е. А\В — АГ\В (рис. 1.28).
Пример 1.13. М = {*■/ t= 1, ..., 5}, Р = {0, 1},
А = {(*i|0.7), (*а|0.1), (*з|1.0), (*<|0.0), (*«10.7)},
В = {(*i|0.2), (*а|0.8), (*3|1.0), (*«|0.3), (*.|0.6)},
В = {(*i|0.8), (*а|0.2), (*3|0.0), (*«|0.7), (*в|0.4)},
А\В = {(ii|0.7), (i2|0.1), ( i3|0.0), ( i4|0.0), (*s|0.4)}.
§1.9. Нечеткие подмножества
79
Введенные операции дополнения, пересечения и объединения
удовлетворяют законам:
коммутатт н ости
AU B = В U А, А(~\В = ВГ\А]
ассоциативности
AU(BUC) = (AUB)UC, АП(ВПС) = (АПВ)ПС;
идемпотентности
A U A = A, АГ\А = А]
дистрибутивности
А П (В U С) = А П В U А П С, A U В П С = [A U В) П (A U С);
действия с константами
А П 0 = 0, A U 0 — А;
0 — пустое множество, 0 «->• (Vxj)(/i0(xi) = 0),
A ni^A , A U l = l,
1 — универсальное множество, 1 <4 (V*i)(/*i(*;) = 1);
двойного дополнения (инволюции)
А = А;
де Моргана
А п В = AUB, AUB = АГ\В]
поглощения
АиАГ\В = А, Ап{АиВ) = А.

Докажем, например, закон поглощения:
АиАПВ <-» m ax(/i^(i), min(/ix(i), /*в(я))).
При ца(х) > Цв{х) имеем шах(^д(х), цв(х)) = Ца(х) «4 А.
При ца{х) < цв(х) имеем m ax(/ix(i), Ца{х)) = ца(х) <-* А.
Выше было показано, что булеан В(1) универсального множе
ства 1 является дистрибутивной решеткой с дополнениями, т. е.
булевой решеткой. Однако множество нечетких множеств является
дистрибутивной решеткой без дополнений; соотношения
АПА = 0, AUA = 1 (1.9)
в этом случае не выполняются.
В силу несправедливости соотношений (1.9) в этой решетке не
выполняются законы склеивания
АПВиАПВф A, (AU В) П {AUB) ф А
и законы Порецкого
АиАП В = AU В, АП (A U В) = АП В.
Действительно, согласно дистрибутивности пересечения отно
сительно объединения получаем
АП В U АП В = АП (В U В), ВиВф1.
Следовательно,
АпВиАПВфА.
Аналогично доказываются и другие соотношения.
Множество нечетких подмножеств представляет собой вектор
ную решетку.
• ♦
Векторной решеткой называется алгебра (М, х, +), где но
ситель М — множество нечетких подмножеств, сигнатура — one-
рация алгебраического произведения А х В, А,ВсМ:
(Vi € М) (МЛ*В(*) = ^л(х) • liB{x))
и алгебраической суммы А + В, А, В С М:
(Vi € М) (МЛ»В(*) = Va(x) + цв{х) - Ца{х) • Мв(*)).
Пример 1.14. М = {*,/ i — 1, 2, 3, 4}, Р = [0, 1], А, В С М,
Л = {(*,|1.0), (*а|0.1), (а:з)0.8), (14)0.3)},
В = {(*i|0.4), (*а|0.6), (*з|0.0), (*«|0.5)},
А х В = {(*i|0.40), (*2|0.06), (*з|0.0), (^4|0.15)},
А + В = {(jci|1.0), (*г|0.64), (*з|0.8), (ц|0.65)}.
80
____________
Гл. 1. Основы многосортных множеств
____________
