Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§1.6. Аксиоматика теории множеств

Аналитически множество М задается в виде

М — Mi П М2 П Мз U П М2 П Мз U

и Ml П м 7 П Ж и Ml П М2 П Ж и Ml П М2 П Мз

или в виде мографа

GM = (V ,S 3), V = {Mi,M/i = 1,2,3}, S3 С V3,

1 2

{Ml, ~Щ, Мз), {Ml, Ма, Мз), {Ml, Ма, М3} }

3 4 5

(рис. 1.18, б).

В рассматриваемой алгебре А = (-B(l), U, Г), ) операции яв

ляются зависимыми. Действительно, согласно закону де Моргана

любое множество из 2 2 множеств может быть построено и с помо

щью алгебры А = (5(1), U, ). Равносильными в смысле поро

ждения любого множества из 22^ множеств являются алгебры А =

= (-B(l), U, ), А = (В(1), П, ), которые могут быть заменены

соответственно алгебрами А = (B(l), U, \, 1), А = (В(1 ), П, \, 1)

согласно формуле М = 1 \ М, где универсум 1 рассматривается

как нульместная операция.

Алгебра (-B(l), U, \, 1) в силу равенств

МаиМ ь = Ма\*Мь\*{МаПМь),

Ма\Мь = Ма\*{МаПМь)

может быть заменена алгеброй вида (.8 (1 ), П, \*, 1 ).

Рассмотрим задачу минимизации представления множеств в

алгебре Кантора. Пересечение попарно различных множеств П М °‘

называется элементарным. Выражение, задающее множество М

в виде объединения различных элементарных пересечений, на

зывается нормальной формой Кантора (НФК) множества М .

Объединение конституент множества М называется совершенной

НФК множества М .

Минимальной НФК множества М называется НФК этого

множества, имеющая минимальную сложность.

Рассмотрим метод Квайна, который будем использовать для

получения минимальной НФК множества М . Этот метод заключа

ется в последовательном выполнении таких этапов.

1. Выделение максимальных интервалов. Интер

валом множества М называется множество конституент множе

ства М , образующих гиперкуб (некоторой размерности).

Очевидно, что мощность интервала равна степени 2 (т. е. 2°,

2 1 и т. д.).

Гл. 1. Основы многосортных множеств

Запишем, например, множество интервалов для рассмотрен

ного выше примера:

{ООО, 100, 110, Oil, 111, -00, 1-0, 11-, -11}.

Здесь и далее — означает, что множество, соответствующее это

му разряду, в пересечении отсутствует, т. е. по этому множе

ству после объединения соответствующих конституент произошло

склеивание. Например, интервал -00, соответствующий множе

ству конституент 000 и 10 0 , получается в результате преобразова-

ния —— —— —— ——— ——

M l П М2 п М3 U Мх П М2 п Мз = М2 П М3.

Интервал 1а называется максимальным интервалом 1Макс

множества М, если не найдется другого интервала 1р этого мно

жества, содержащего интервал 1а, 1а ф 1р.

В данном случае имеется четыре максимальных интервала:

- 0 0 , 1 - 0 , 1 1 - , - 1 1 ; каждый из них образует гиперкуб размер

ности 1 (ребро).

Пересечение П M f', соответствующее максимальному интер

валу множества М , называется простой импликантой этого мно

жества. Объединение простых импликант множества М называ

ется сокращенной НФК множества М .

Количество первичных термов, образующих простую импли-

канту, называется рангом простой импликанты, а элементарное

пересечение — рангом соответствующего ин

тервала.

При выделении максимальных интерва

лов множество интервалов, имеющих один

и тот же ранг, разбивают на пояса, причем

1-й пояс содержит интервалы, которым соот

ветствуют наборы с » единицами в каждом.

Тогда выделение максимальных интервалов

сводится к сравнению элементов только с о-

седних поясов, номера которых отлича

ются на единицу. Если построенные интервалы не являются мак

симальными, то процесс сравнения продолжают. Результаты срав

нения для рассматриваемого случая приведены на рис. 1.19. Со

кращенная НФК множества М(М\, М2, Мз) имеет вид

М (Mi, М2, Мз) = М2 П Мз U M i П М3 U M i п м 2 и М2 П М3 .

Построением сокращенной НФК множества М заканчивается

первый этап метода Квайна.

Тупиковой НФК множества М называется такая НФК этого

множества, которая при вычеркивании хотя бы одного первичного

терма не определяет М.

Минимальной НФК множества М называется НФК этого

множества, содержащая минимальное количество первичных тер

мов.

Рис. 1.19

§ 1.6. Аксиоматика теории множеств 53

Лемма 1.4. Минимальная НФК множества М является

тупиковой.

Сложность минимальной НФК множества М нельзя умень

шить вычеркиванием первичного терма. Следовательно, эта форма

является тупиковой.

Лемма 1.5. Тупиковая НФК множества М состоит из

простых импликант этого множества.

Если хотя бы одно пересечение соответствует интервалу мно

жества М , не являющемуся максимальным, то это пересечение

можно заменить простой импликантой вычеркиванием соответ

ствующих первичных термов, не выходя из класса эквивалент

ных НФК (задающих одно и то же множество) множества М , что

противоречит определению тупиковой НФК.

Теорема 1.Т. Тупиковые НФК множества М , в том числе

и минимальная НФК, содержатся в сокращенной НФК

этого множества.

Тупиковая НФК множества М , в том числе и минимальная

НФК, состоит согласно лемме 1.5 из простых импликант. Сокра

щенная НФК множества М включает все простые импликанты.

Следовательно, тупиковая (минимальная) НФК множества М со

держится в сокращенной НФК этого множества.

Согласно теореме 1.7 построение тупиковой НФК множества М

сводится к покрытию двумерной таблицы.

Покрытием столбцов строками в двумерной таблице назы

вается такое множество строк, при котором для каждого столбца

найдется хотя бы одна строка из этого множества, на пересечении

с которой этот столбец имеет единицу, причем при вычеркивании

хотя бы одного элемента из этого множества строк указанное свой

ство не выполняется.

2. Построение и покрытие таблицы Квайна. Таб

лица Квайна — двумерная таблица, каждой строке которой вза

имно однозначно соответствует максимальный интервал, столб

цу — конституента, а на пересечении »-й строки и j-го столбца

находится единица, если j -я конституента входит в г-й максималь

ный интервал, в противном случае клетку (i, j) не заполняют или

ставят в ней 0 .

Для рассматриваемого примера таблица Квайна имеет вид

табл. 1.15.

Таблица 1.15

Максимальный

интервал

Конституента

ООО

100

110

011

111

-00

1-0

1 1

11-

-11

1 1

Гл. 1. Основы многосортных множеств

Максимальный интервал называется обязательным, если най

дется конституента, принадлежащая ему и только ему. Столбец,

соответствующий этой конституенте, содержит только одну еди

ницу. Множество обязательных интервалов образует ядро покры

тия.

В данном случае ядром покрытия является множество {-00,

— 1 1 }, которое покрывает первый, второй, четвертый и пятый сто

лбцы. Для образования покрытия можно взять либо вторую, либо

третью строку. В результате получаем два покрытия: {—00, —11,

1 - 0 }, { - 0 0 , —1 1 , 1 1 -} ; каждое из них является минимальным и

имеет сложность 6 . Для определенности выберем первое из покры

тий, которое соответствует минимальной НФК, задающей множе

ство М(М\, М2, М3) = М2 Г)Мз UМ 2 Г)М3 UMi ПМз. В результате

упрощения сложность L(M) уменьшилась от 15 до 6 .

Минимальная НФК находится в результате перебора всех по

крытий, осуществляемого с помощью преобразования мультипли

кативно-аддитивной формы в аддитивно-мультипликативную

форму.

Для рассматриваемого примера обозначим четыре строки

табл. 1.15 соответственно буквами а, Ъ, с, d. Запишем множество

строк, каждый элемент которого покрывает j-Vi столбец:

j = 1 -)■ Ai = -fa}, j = 2 А2 = {a, 6},

j = 3 ->• A3 = {b, c}, j = 4 A4 = {d}, j = 5-+ As = {c, d).

Покрытием столбцов строками этой таблицы является множество

строк, покрывающее все столбцы таблицы, и при удалении хотя

бы одной из этих строк найдется непокрытый столбец. Следова

тельно, если каждое множество Aj представить в виде объедине

ния его элементов и найти пересечение всех множеств Aj, П Aj,

то каждое пересечение в полученной аддитивной форме соответ

ствует покрытию, а число всех покрытий равно числу различных

пересечений в полученной аддитивно-мультипликативной форме:

П А , =an(aU6)D(6 Uc)ndn(cUd) =

= an(6 (Jc)nd=an6 ndUancncf.

Полученные пересечения aHbndnancDd порождают два

покрытия: { - 0 0 , 1 - 0 , - 1 1 } и { - 0 0, 1 1 - , - 1 1 }; каждое из них со

ответствует минимальной НФК заданного множества М. Дальней

шее уменьшение сложности выражения, определяющего заданное

множество, возможно, если из класса НКФ перейти в класс скобоч

ных форм Кантора (СФК). Выражение, определяющее множество

М, называется скобочной формой Кантора, если кроме первич

ных термов и знаков операций объединения и пересечения в него

входят круглые скобки.

§1.7. Алгоритм — двусортное множество. Системы счисления 55

В рассматриваемом примере сложность представления множе

ства, равная 6 , понижается до 5 в результате применения закона

дистрибутивности пересечения относительно объединения:

M(Mi, М 2, М3) = М3 П (Mj U М2) U М2 П М3.

Преобразование мультипликативно-аддитивной формы в адди-

тивно-мультипликативную называется методом Петрика, кото

рый может быть определен соответствующим алгоритмом.

§ 1.7. Алгоритм — двусортное множество.

Системы счисления

Важным классом многосортного множества является класс,

элементами которого являются алгоритмы. Слово “алгоритм” (al

gorithm) является латинской транслитерацией арабского имени

хорезмского математика IX века аль-Хорезми.

Дадим интуитивное определение алгоритма. Алгоритмом

называется двусортное множество (Мр, R2), где Мр — множество

правил (процедур) решения задачи, обладающих следующими

свойствами:

массовости — инвариантности относительно входной инфор

мации;

детерминированности — однозначности применения этих

правил на каждом шагу;

результативности — получения после применения этих пра

вил информации, являющейся результатом;

элементарности (прозрачности) — отсутствия необходимости

дальнейшего уточнения правил.

Символ R 2 — бинарное отношение в множестве М р, R 2 С М 2,

(pi,pj) € # 2 , если после процедуры р,- выполняется процедура pj.

Алгоритм можно представить в виде графа, каждая вершина

которого соответствует правилу, и бинарное отношение R 2 опреде

ляет порядок выполнения этих правил. Бели при этом вершина

является началом или концом только одной дуги, то правило назы

вается арифметическим. Если правило является концом только

одной дуги, а началом — более чем одной дуги, то правило называ

ется логическим. После выполнения логического правила проис

ходит ветвление вычислительного процесса согласно полученному

результату.

Первоначально построение алгоритма нельзя выполнить пол

ностью формальным образом. Это — искусство. Рассмотрим, на

пример, построение алгоритма перевода целых чисел, заданных

в десятичной системе счисления, в систему счисления с основа

нием 5. Как строить алгоритм, будет понятно, если догадаться,

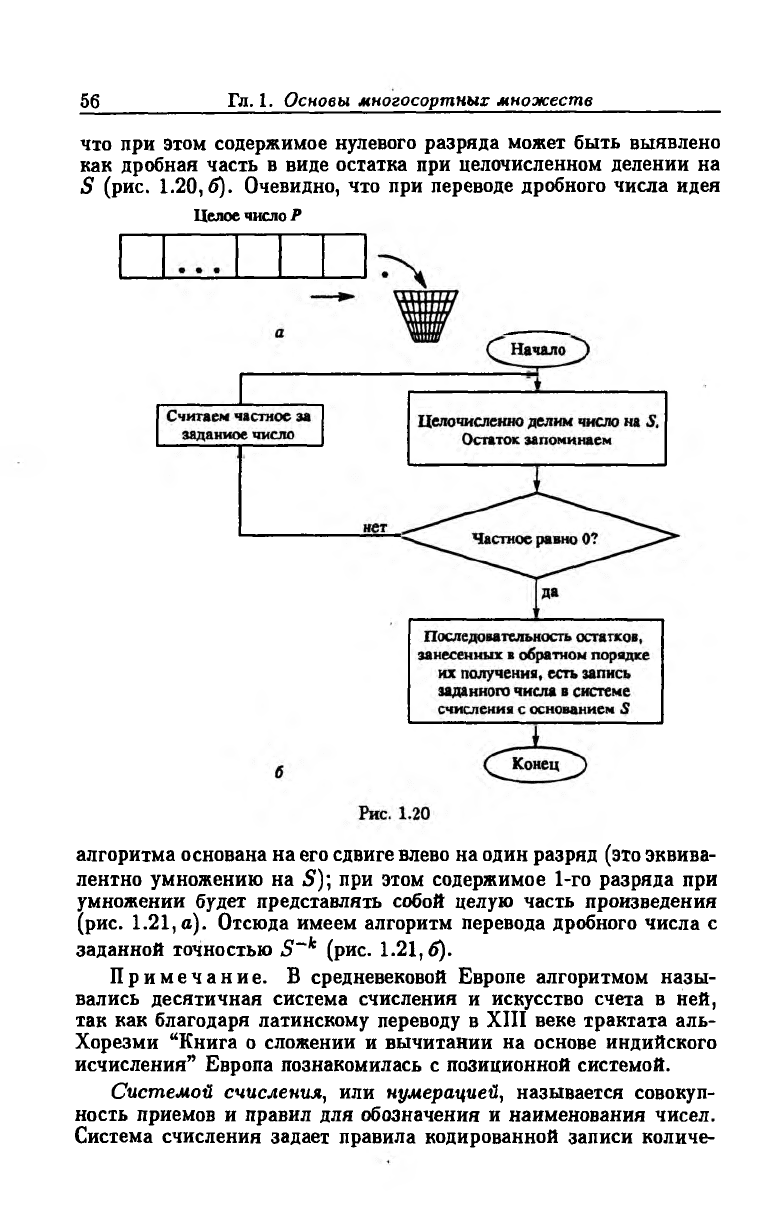
что сдвиг на один разряд вправо целого числа (рис. 1 .2 0 , а) экви

валентен делению этого числа на основание системы счисления и

Гл. 1. Основы многосортных множеств

что при этом содержимое нулевого разряда может быть выявлено

как дробная часть в виде остатка при целочисленном делении на

5 (рис. 1.20,6). Очевидно, что при переводе дробного числа идея

Целое число Р

алгоритма основана на его сдвиге влево на один разряд (это эквива

лентно умножению на 5); при этом содержимое 1 -го разряда при

умножении будет представлять собой целую часть произведения

(рис. 1 .2 1 , а). Отсюда имеем алгоритм перевода дробного числа с

заданной точностью S~k (рис. 1 .2 1 , б).

Примечание. В средневековой Европе алгоритмом назы

вались десятичная система счисления и искусство счета в ней,

так как благодаря латинскому переводу в XIII веке трактата аль-

Хорезми “Книга о сложении и вычитании на основе индийского

исчисления” Европа познакомилась с позиционной системой.

Системой счисления, или нумерацией, называется совокуп

ность приемов и правил для обозначения и наименования чисел.

Система счисления задает правила кодированной записи количе

§ 1.7. Алгоритм — двусортное множество. Системы счисления 57

ственных эквивалентов, позволяющие для каждого числа одно

значно получать его кодовую запись и по каждой кодовой записи —

соответствующий ей количественный эквивалент. По соглашению

Дробное число

Последовательность целых частей

произведений, записанная в прямом

порядке их получения, есть запись

заданного числа в системе счисления

с основанием S

Конец

Рис. 1.21

количественный эквивалент записывается в десятичной системе

счисления. Множество элементарных знаков, используемых для

кодирования, называют цифрами счисления.

Слово “цифра” — от арабского слова “сыфр”, которое в свою

очередь является переводом древнеиндийского слова (алфавит “де-

ванагари”) “сунья”, что означает пустое место (разряд), в которое

помещается числовой знак при задании количественных отноше

ний.

Системы счисления бывают непозиционные и позиционные. В

непозиционных системах каждой цифре сопоставлен некоторый

стандартный количественный эквивалент, а количественный эк

вивалент кода числа вычисляется как некоторая функция от ко

личества эквивалентных цифр, входящих в запись этого кода.

Примером такой системы является система счисления, в которой

Гл. 1. Основы многосортных множеств

используется только одна цифра, например I. Этой цифре сопо

ставлен количественный эквивалент, равный единице. Тогда код

1ПШ означает количественный эквивалент шести, функцией при

вычислении количественного эквивалента кода здесь является опе

рация сложения.

В позиционных системах каждой цифре некоторый количествен

ный эквивалент сопоставляется не однозначно, а в зависимости

от ее положения в коде числа. Будем рассматривать только ли

нейно упорядоченные записи. Выберем в записи начало отсчета

(нулевой разряд). Разряды влево от него будем нумеровать 1 ,

2, ..., а вправо от него -1 , -2 , ... Каждой цифре а,-, стоящей

в разряде с номером j, сопоставляется количественный эквива

лент <p(aij). Функция либо одинакова для всех разрядов, либо

ее вид изменяется от разряда к разряду. В дальнейшем будут рас

сматриваться только позиционные системы с одинаковой функ

цией всех разрядов. Всякая позиционная система задается тремя

компонентами: (А, <р, F). Здесь А — множество цифр системы;

<р — функция, определяющая для цифр в каждом разряде их ко

личественный эквивалент; F — функция, определяющая по коли

чественным эквивалентам в записи числа количественный экви

валент самого числа.

В зависимости от вида функции F выделим системы счисле

ния двух типов: аддитивные к мультипликативные. В системах

первого типа F — функция сложения, а в системах второго ти

па — функция умножения.

Если для любых цифр А и любого j имеет место равенство

¥>(а«! j) — S' ■ <р(а{, 0 ), то говорят о системе счисления с основа

нием S.

Если <p(ai, j) = pj ■ ip(ai, 0) и pj не совпадают при различных

j, то система весомозначного типа, a pj — веса разрядов.

Если в системе с основанием S множество цифр состоит из 0,

1,..., 5 —1, то система имеет естественное множество цифр (есте

ственная система счисления); если S = m + + 1 и множе

ство цифр — {—ш, -in -f 1 , ..., - 1 , 0 , 1 , 2 , ..., к}, то при т = к

система имеет симметрическое множество цифр (симметрическая

система счисления); при к > т или т > к система4 имеет асим

метрическое соответственно в положительную или отрицательную

сторону множество цифр (асимметрическая система счисления).

Наиболее часто используют естественные системы счисления с

натуральным основанием. Любое число х в системе с основанием

S представимо в следующем виде:

ОО

*= Е w-s‘.

1ST—ОО

где [а,] — количественный эквивалент цифры о,- в нулевом раз

ряде.

§1.7. Алгоритм — двусортное множество. Системы счисления 59

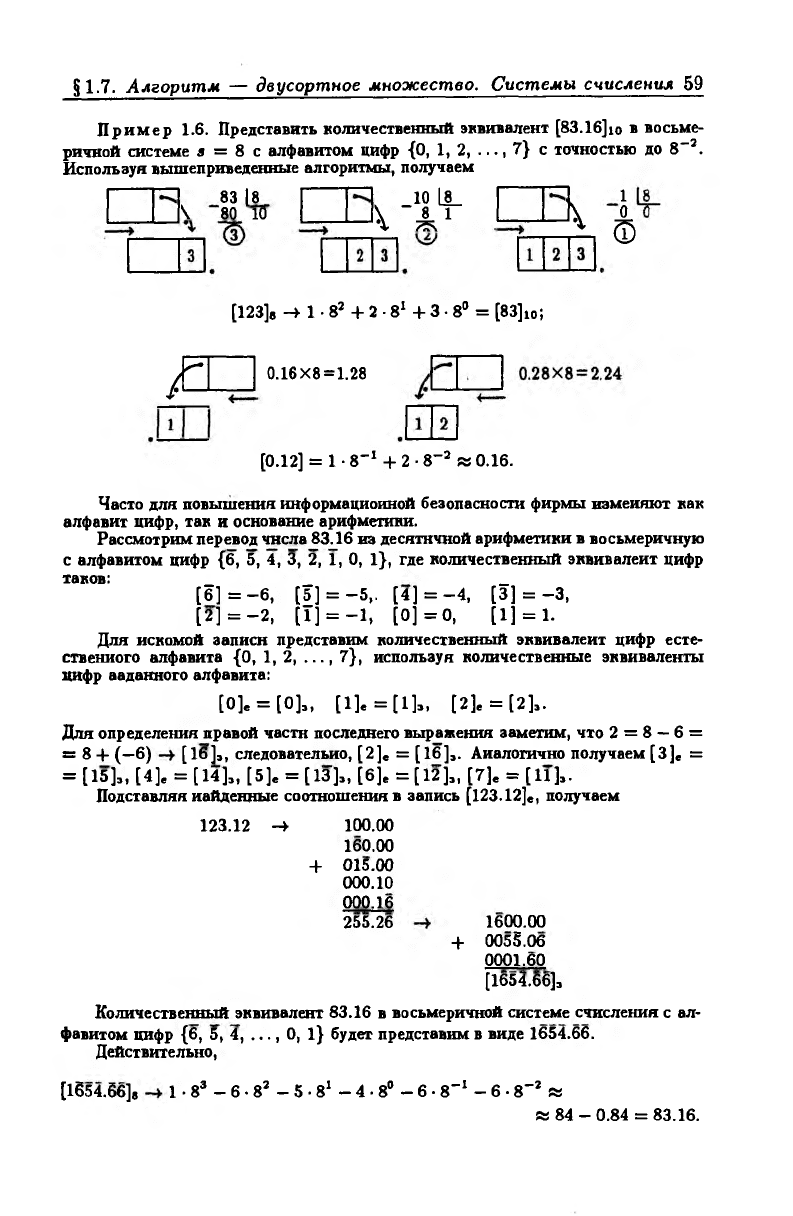
Пример 1.6. Представить количественный эквивалент [83.16]ю в восьме

ричной системе 5 = 8 с алфавитом цифр {0, 1, 2, ..., 7} с точностью до 8~2.

Используя вышеприведенные алгоритмы, получаем

83 18

Ч 80 КГ

v - 12 15-

\ А 1 .

[123]* - И • 82 + 2 • 81 + 3 • 8° = [83]ю;

0.16X8=1.28

[0.12] = 1 ■ 8-1 + 2 • 8~2 « 0.16.

Часто для повышения информационной безопасности фирмы изменяют как

алфавит цифр, так и основание арифметики.

Рассмотрим перевод числа 83.16 из десятичной арифметики в восьмеричную

с алфавитом цифр {6, 5, 4, 3, 2, 1, 0, 1}, где количественный эквивалент цифр

таков: _ _ _

[6] = -6 , [5] = -5,. [4] = -4 , [3] = -3,

[2] = -2, [I] = -1, [0] = 0, [1] = 1.

Для искомой записи представим количественный эквивалент цифр есте

ственного алфавита {0, 1,2, ..., 7}, используя количественные эквиваленты

цифр ааданного алфавита:

[0 ]е = [0 ]„ [1 ]е=[1 ]„ [2 ], =[2 ],.

Для определения правой части последнего выражения заметим, что 2 = 8 — 6 =

в 8 + (—6) [16 ]3, следовательно, [2]е = [ 16 ]3. Аналогично получаем [3]е =

= [15]»1 [4]е = [14 ]э> [5]е = [13 ]j, [6]е = [12 ]э, [7]е = [H ]j-

Подставляя найденные соотношения в запись [123.12]е, получаем

123.12 -¥ 100.00

160.00

+ 015.00

000.10

000.16

255.26 1600.00

+ 0055.06

0001.60

[1654.66],

Количественный эквивалент 83.16 в восьмеричной системе счисления с ал

фавитом цифр {6, 5, 4, ..., 0, 1} будет представим в виде 1654.66.

Действительно,

[1б54.б6]* 1 • 83 - 6 • 82 - 5 • 81 - 4 • 8° - 6 • 8-1 - 6 • 8-2 «

«84-0.84 = 83.16.

Гл. 1. Основы многосортных множеств

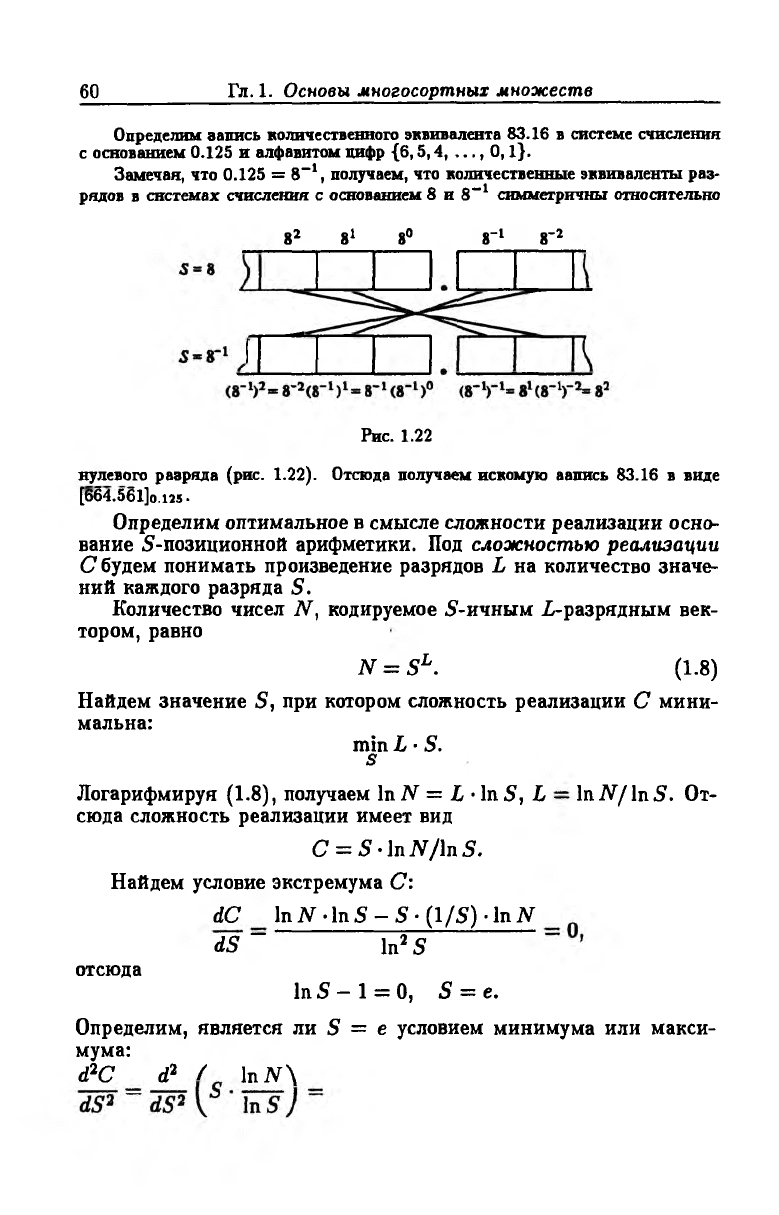
Определим запись количественного эквивалента 83.16 в системе счисления

с основанием 0.125 и алфавитом цифр {6,5,4, ..., 0,1}.

Замечая, что 0.125 = 8-1, получаем, что количественные эквиваленты раз

рядов в системах счисления с основанием 8 и 8-1 симметричны относительно

82 81 8° 8-1 8 '2

Рис. 1.22

нулевого разряда (рис. 1.22). Отсюда получаем искомую аапись 83.16 в виде

[664.561]o.im .

Определим оптимальное в смысле сложности реализации осно

вание S-позиционной арифметики. Под сложностью реализации

С будем понимать произведение разрядов L на количество значе

ний каждого разряда 5.

Количество чисел N, кодируемое 5-ичным i -разрядным век

тором, равно

N = SL. (1.8)

Найдем значение 5, при котором сложность реализации С мини

мальна:

min L • 5.

Логарифмируя (1.8), получаем In N = L • In 5, L — InN/lnS. От

сюда сложность реализации имеет вид

С = S 'InN/lnS.

Найдем условие экстремума С:

dC In iV • In 5 — 5 • (1/5) • In N

dS ~ In2 5

отсюда

In 5 - 1 = 0, 5 = e.

Определим, является ли 5 = e условием минимума или макси

мума:

d2C d? / In iV\