Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

Введение 11

которой символы используемой системы счисления или логики мо

делируются различными состояниями атомов, причем масса ЭВМ

равна массе Земли, то на основании общих законов физики эта

ЭВМ не сможет даже в течение всех геологических эпох перерабо

тать больше 1073 двоичных разрядов информации [25]. При реше

нии же N P -полных задач реальной размерности объем перераба

тываемой информации превышает величину 1073. Этот факт вы

звал пессимизм среди математиков-теоретиков, которые акценти

ровали внимание в основном на исследовании понятийного уровня

дискретной математики и асимптотических зависимостей.

Математики-прикладники направили усилия на разборку ал

горитмов решения задач дискретной математики, что диктуется

практической потребностью ускоренного движения от физического

смысла задачи к алгоритмическим построениям и широкому ис

пользованию ЭВМ.

При решении проблемы уменьшения перебора вариантов име

ются группы алгоритмов: эвристические и характеризационные.

К эвристическим относятся алгоритмы широкого класса, начиная

от ГСН-алгоритмов (ГСН — грубая сила и невежество) и кончая

“хитрыми”, “жадными” и другими эвристическими алгоритмами.

Название алгоритма соответствует тому виду эвристики, ко

торый определяет процедуру борьбы с перебором. Оценить, на

сколько удалено полученное с помощью эвристического алгоритма

решение от минимального в смысле значений функционала каче

ства решения, принципиально невозможно. От этого существен

ного недостатка свободны характеризационные алгоритмы, струк

тура которых была предложена автором в 60-х годах [9]. На осно

вании характеризации проводимых комбинаторных преобразова

ний можно найти минимальное решение без поиска всех эквива

лентных решений, исключая их перебор.

Характеризационный алгоритм решения задачи состоит из

процедуры эквивалентирования и фактического получения реше

ния. Первая процедура состоит в преобразовании исходной ин

формации к виду, при котором, фактически не строя решения,

можно вычислить функционал его качества. Трудоемкость ха-

рактеризационных алгоритмов для практических задач оценива

ется полиномиальными функциями, степень которых не превы

шает 3-5. Расхождение полученных результатов с результатами,

полученными математиками-теоретиками, объясняется двумя

причинами. Во-первых, математики-теоретики оценивают трудо

емкость алгоритмов решения комбинаторной задачи экспоненци

альной зависимостью, исходя из наихудшего случая, который, как

правило, является искусственным, не имеющим на практике ме

ста, и, во-вторых, доказывают асимптотические оценки, т. е. рас

сматривают предельный переход при п —> со (п — размерность

задачи). Практически же размерность задачи является конечной

Введение

величиной. Например, получение экспоненциальной оценки тру

доемкости раскраски вершин произвольного графа сновано на зна

нии максимального числа /(п) пустых подграфов в графе с п вер

шинами:

З"/3, п = 0 (mod 3),

f(n) = 4 • 3<”"4)/3, п = l(mod3),

2 • з("-2)/3, п = 2(mod3),

но эта зависимость справедлива только для графов единственного

класса, являющихся дополнениями графов Муна—Мозера до пол

ных.

Комбинаторные задачи необходимо рассматривать, принимая

во внимание исходную конкретную информацию, и на ее базе

разрабатывать интеллектуальные информационные технологии и

стратегии их решения.

Подобно тому как дар слова обогащает нас

мнениями других, гак язык математиче

ских знаков служит средством, еще более

совершенным, более точным и ясным...

Н.Н. Лобачевский

Глава 1

ОСНОВЫ МНОГОСОРТНЫХ МНОЖЕСТВ

§ 1.1. Множество, функция, операция.

Способы задания

Любое понятие дискретной математики можно определить с

помощью понятия множества. Под множеством понимают объ

единение в одно общее объектов, хорошо различаемых нашей ин

туицией или нашей мыслью. Таково интуитивное определение

понятия множества, данное основателем теории множеств Геор

гом Кантором. Это понятие является в математике первичным

и, следовательно, не имеет строгого определения. Объекты, кото

рые образуют множество, будем называть элементами множества

и обозначать, как правило, малыми буквами латинского алфави

та. Если элемент т принадлежит множеству М, то будем ис

пользовать запись т € М , в противном случае используем запись

m ^ М; знак € принадлежности элемента множеству является сти

лизацией первой буквы греческого слова ест, (есть, быть).

Множество, содержащее конечное число элементов, называется

конечным. Если же множество не содержит ни одного элемента,

то оно называется пустым и обозначается 0 .

Множество может быть задано различными способами: пере

числением элементов (конечные множества) или указанием их

свойств (при этом для задания множеств используют фигурные

скобки). Например, множество М цифр десятичного алфавита

можно задать в виде М — {0, 1 , ..., 9} или М = {i/ i целое,

О < г < 9 }, где справа от наклонной черты указано свойство эле

ментов этого множества. Множество М четных чисел можно за

писать в виде М = {тп/ т — четное число}.

Множество М ' называется подмножеством множества М (М'

включено в М ) тогда и только тогда, когда любой элемент множе

ства М ' принадлежит множеству М:

М ' СМ*-}(т£М'~>т£ М)

или

М 'с М « М '= {гп{( гщ € М};

здесь С — знак включения подмножества; а —► Ъ означает: если

а, то Ь; а <-> b означает: Ь, если и только если а. В частном случае

множества М ' и М могут совпадать.

Гл. 1. Основы многосортных множеств

Невключение подмножества М ' в множество М обозначается

М £ М.

Очевидно, что если множество М а — подмножество множества

Мь и множество Мь — подмножество множества М а, то оба этих

множества состоят из одних и тех же элементов. Такие множества

называются равными: Ма = Мь- Если же множество М ' — под

множество множества М, а множество М не является подмноже

ством множества М ', то множество М ' называется собственным

подмножеством множества М; запись: М ' СС М .

Для каждого множества М существует множество, элементами

которого являются подмножества множества М, и только они. Та

кое множество будем называть семейством множества М или

булеаном этого множества и обозначать В(М), а множество М бу

дем называть универсальным, универсумом или пространством

и обозначать 1 .

При рассмотрении различных подмножеств и их свойств часто

приходится обращаться к комбинаторике — разделу дискретной

математики, посвященному решению задач выбора и расположе

ния элементов некоторого, как правило, конечного множества в

соответствии с заданными свойствами.

Каждое такое свойство определяет способ построения некото

рой конструкции из элементов множества, называемой комбина

торной конфигурацией. Простейшими комбинаторными конфи

гурациями являются размещения, перестановки и сочетания.

Размещение А(п, К) мощности К из п элементов (К < п) —

это любая последовательность (т. е. множество с зафиксирован

ным в нем порядком элементов) попарно различных К элемен

тов, взятых из п элементов; для записи размещений используются

круглые скобки.

Первый элемент последовательности можно зафиксировать п

способами, второй элемент — п - 1 способами и т. д., К -й эле

мент — п — К + 1 способами. Следовательно, количество таких

последовательностей (размещений) равно произведению чисел п,

п - 1 , ..., п - К + 1 : К 1

|A(n, JiQ| = п • (п - 1) •... • (п - К + 1) = Л (п - г).

1=0

В этой конфигурации важен как состав элементов, так и их по

рядок.

Размещение при К = п называется перестановкой Р(п). Чи

сло перестановок |Р(п)| из п элементов есть

П — 1

(п — г) = п • (тг — 1 ) •... • 2 • 1 = п\.

i=o

Сочетанием С(п, К) мощности К из п элементов называется

любое подмножество, содержащее К элементов, набранных из п

§ 1.1. Множество, функция, операция. Способы задания

элементов. В сочетании важен только состав элементов, порядок

же не играет роли. Очевидно, что число размещений из п по К,

содержащих одни и те же К элементов, равно К \, так как эти раз

мещения отличаются друг от друга только порядком. Такие раз

мещения соответствуют одному сочетанию. Следовательно, число

сочетаний из п по К элементов есть

|А (п,К )| п!

Р(К)

\С{п,К)\

(п - К)\ ■ К\

Это число, кстати, равно К-иу коэффициенту в разложении би

нома Ньютона (а+ Ь)п.

Рассмотрим образование булеана 5(1) от универсума 1 = {у,

х, а}. Первым множеством является пустое множество 0, не со

держащее ни одного элемента. Образуем затем (^ ) — число соче

таний из |1 | по 1 — множеств, содержащих по одному элементу,

Затем образуем (^ ) множеств, содержащих по два элемента, и

т. д., наконец, образуем множество, содержащее все элементы мно

жества 1. Здесь |1 | — количество элементов конечного множества

1 , в дальнейшем называемое мощностью множества.

Очевидно, что мощность |В(1)| булеана от универсума 1 рав

на 2 W;

|B(1 )| = 2 W.

В рассматриваемом случае 5(1) = {0 , {у}, {х}, {а}, {у,х}, {а,х},

{а.У}. {У,над

множество также часто задают графически с помощью диа

грамм Эйлера. Например, задание множества {{а, Ь, с}, {b, d, е}}

в пространстве 1 = {а, Ь, с, d, е}

приведено на рис. 1 .1 , где зам

кнутые линии, называемые в

дальнейшем кругами Эйлера, ог

раничивают элементы множест

ва, при этом рамка, в верхнем

правом углу которой стоит 1 , ог

раничивает элементы простран

ства.

Другие способы задания мно

жеств будут рассмотрены по мере

необходимости.

Одним из важнейших понятий теории множеств является по

нятие декартова произведения множеств. Декартовым произве

дением М а X Мь множеств М а и Мь называется множество вида

М = {(mi, rrij)/ mi € Ма, rrij € Мь}.

Рис. 1.1

Гл.1. Основы многосортных множеств

Подмножество.F С Му х Мх называется функцией, если для

каждого элемента х <Е Мх найдется не более одного элемента

у € Му вида (у, х) € F, при этом функция называется всюду

(полностью) определенной; в противном случае функция назы

вается частично определенной (недоопределенной). Множество

Мх образует область определения функции F, множество Му —

область значений функции F. Часто вместо записи (у,*) € F

используют запись у = F (x); при этом элемент х называют аргу

ментом или переменной, а у — значением функции F.

Сопоставим с декартовым произведением двух множеств пря

моугольную решетку, узлы которой взаимно однозначно соответст

вуют элементам декартова произведения. Подмножество декартова

произведения на рисунках будем отмечать зачернением соответ

ствующих элементов.

П ример 1.1. На рис. 1.2,а изображено подмножество декартова произве

дения множеств Му = {yi, У2, уз, и Мх = { ц , 1 2 , хз}, не являющееся

Рис. 1.2

функцией, на рис. 1.2,6 — подмножество, являющееся полностью определенной

функцией, на рис. 1.2, в — частично определенной функцией.

Количество аргументов определяет местность функции. Выше

были рассмотрены одноместные функции.

Аналогично понятию декартова произведения двух множеств

определим декартово произведение п множеств.

Декартовым произведением

Mi х М2 х ... х Мп = Д М, ,

*=1

множеств М\ , М 2, ..., М„ называется множество

м = {(muim,-2, . ..,m,-n)/ mVl G М и т ^ G M2). ..,min € Mn}.

Элементами декартова произведения М г х М2 х ... х Мп

являются всевозможные последовательности, каждая из которых

S 1.1. Множество, функция, операция. Способы задания

состоит из п элементов, причем первый элемент принадлежит мно

жеству M i, второй — множеству Мг и т. д., n-й элемент принад

лежит множеству Мп.

Если множество Мх в определении функции у = F(x) явля

ется декартовым произведением множеств МХ1, МХ2, ..., МХп, то

получим определение п-местной функции:

у = F(xi, х2, ..., *„).

Частным случаем га-местной функции у = F(xi,x2,..., ®п) яв

ляется п-местная операция. Под п-местной операцией Оп в мно

жестве М понимается п-местная функция у = F(x 1 , а:2, • • •, *п),

у которой области определения аргументов и область значений

функции совпадают:

-А^/х| —— "■ . ■ - — Л</д;п —— Л^у.

Таким образом, n-местная операция по п элементам множества М

определяет (n -f 1 )-й элемент этого же множества.

Рассмотрим пространство 1 и определим в нем четыре опера

ции над множествами: объединение, пересечение, разность, до

полнение.

Объединением M aUM(, двух множеств М а и Мь является мно

жество М, состоящее из элементов множества М а и из элементов

множества Мь:

М = М а U Мь = {m,/ тп, £ Ма и/или тп,- £ Мь}.

Пересечением МаПМь двух множеств Ма и Мь является мно

жество М, состоящее из элементов, которые принадлежат как мно

жеству Afa, так и множеству Мь:

М = МаГ\Мь = {тп,/ тп,- € Ма и т , е Мь};

часто союз “и” заменяют знаком &:

М = Ма П Мь = {тп,/ mi € Ма & т , 6 Мь}.

Разностью М а \ Мь множеств М а и Мь является множество

М, состоящее из элементов, принадлежащих множеству Ма и не

принадлежащих множеству Мь’.

М = Ма\М ь = {тп,/ тп, £ М а к тп,’ g Мь).

Введенные операции являются двуместными.

Рассмотрим операцию дополнения, являющуюся одноместной.

Дополнением М множества М является множество

М = {тп,/ тп,- £ М}.

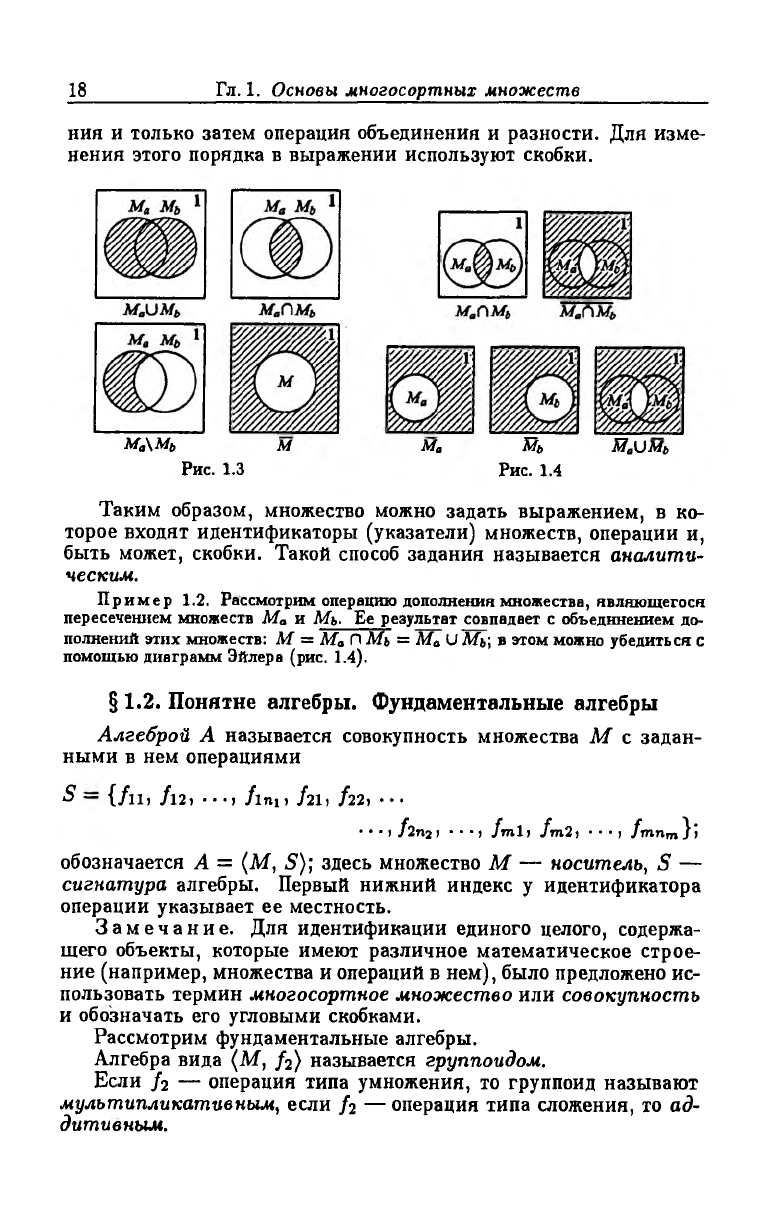
Операции объединения, пересечения, разности и дополнения

проиллюстрированы на рис. 1.3; результирующее множество каж

дой операции выделено штриховкой. Используя эти операции,

можно выражать одни множества через другие, при этом сначала

выполняется одноместная операция дополнения, затем пересече-

Гл. 1. Основы многосортных множеств

ния и только затем операция объединения и разности. Для изме

нения этого порядка в выражении используют скобки.

ма\м„ м ма Шъ Да им*

Рис. 1.3 Рис. 1.4

Таким образом, множество можно задать выражением, в ко

торое входят идентификаторы (указатели) множеств, операции и,

быть может, скобки. Такой способ задания называется аналити

ческим.

Пример 1.2. Рассмотрим операцию дополнения множества, являющегося

пересечением множеств Ма и Мь- Ее результат совпадает с объединением до

полнений этих множеств: М = Ма П Мь = Ма U Мь\ в этом можно убедиться с

помощью диаграмм Эйлера (рис. 1.4).

§ 1.2. Понятие алгебры. Фундаментальные алгебры

Алгеброй А называется совокупность множества М с задан

ными в нем операциями

S — {/ш / 12 , • • •) /in i, / 2 1) / 22, • • •

• • •) / 2nj) • • •) /m l) /m2) • • •) /rnnm}’)

обозначается А = (М , 5); здесь множество М — носитель, S —

сигнатура алгебры. Первый нижний индекс у идентификатора

операции указывает ее местность.

Замечание. Для идентификации единого целого, содержа

щего объекты, которые имеют различное математическое строе

ние (например, множества и операций в нем), было предложено ис

пользовать термин многосортное множество или совокупность

и обозначать его угловыми скобками.

Рассмотрим фундаментальные алгебры.

Алгебра вида (М , / 2) называется группоидом.

Если /2 — операция типа умножения, то группоид называют

мультипликативным, если /2 — операция типа сложения, то ад

дитивным.

§1.2. Понятие алгебры. Фундаментальные алгебры

Пусть А = (М , / 2) — группоид; обозначим операцию / 2 как о.

Тогда элемент е € М называется правым нейтральным элемен

том группоида А, если для всякого элемента т k М выполняется

равенство т о е = т , и левым нейтральным элементом, если

е о т = т .

Если элемент е € М группоида А = (М, о) является одновре

менно и левым, и правым нейтральным элементом, то его назы

вают двусторонним нейтральным элементом или просто ней

тральным элементом. Никакой группоид не может иметь бо

лее одного нейтрального элемента. Действительно, если т о е —

= е о т = тпи тое' — е'от — т справедливо для всех m 6 М,

то е' = е' о е = е.

Если группоид (М, о) мультипликативный, то нейтральный

элемент называется единицей и обозначается 1 ; если группоид

(М, о) аддитивный, то нейтральный элемент называется нулем

и обозначается 0 .

Группоид А = (М, о) называется идемпотентным, если его

сигнатура удовлетворяет закону идемпотентности

(Vm 6 М)(то т= т).

Группоид А = (М , о), сигнатура которого удовлетворяет за

кону коммутативности

(Vx, у € М )(я о у = у о х),

называется коммутативным или абелевым.

Группоид (М, о), в котором выполняется закон ассоциатив

ности

(Vz, у, z е М) (ж о (у о z) = (ж о у) о z) ,

называется ассоциативным или полугруппой.

Полугруппа (М, о), в которой выполнимы обратные операции,

т. е. для любых a, b k М каждое из уравнений а о х = Ь, у о а = Ь

обладает единственным решением, называется группой.

Проиллюстрируем понятие группы на примере группы подстановок, содер

жащей шесть элементов. Группу подстановок исследовал выдающийся фран

цузский математик Эварист Галуа в связи с решением уравнений в радикалах.

Подстановкой п-й степени называется взаимно однозначное отображение мнсъ

жества из п элементов на себя.

Рассмотрим три элемента: xi, 12, хз. Существует шесть перестановок из

трех элементов: Х1Х2Х3, Х2Х3Х1, Х1Х3Х2, хзх\хг, Х2Х1Х3, ХЗХ2Х\. Запишем две

перестановки нз трех элементов друг под другом:

(

Х\ Х2 * з\

Х2 Хз XI)

Эта запись означает, что х\ переходит в Х2, хг — в хз, хз — в х\.

Число возможных подстановок равно числу перестановок. Введем следую

щие обозначения для шести возможных подстановок:

(х\ Х2 Х з\ L _ Х2 Хз\ (Х\ Х2 ХЗ^

VXl Х2 Хз) ’ \&l Хз Xi) ’ \Х2 Х\ Хз) ’

J _ (х\ Х2 Х з\ _ (х\ Х2 * з \ г _ (Х\ Х2 Яз\

VX2 Хз XI) ’ \Хз Xl Xi) ’ 1 V* 3 Х2 Х\) '

Гл.1. Основы многосортных множеств

Введем операцию умножения х над подстановками. Произведением под

становок называется подстановка, получаемая в результате последовательного

выполнения сначала первой, а затем второй из перемножаемых подстановок. На

пример,

c x u f ^ 1 XJ х (? XJ ? ) х (? *»

\Х2 XI хг) 4*1 х 3 Х2/ \Хз Xl X?)

Значения выражения а х /? , где а, /3 = а, Ъ, с, d, е, /, представлены л

табл. 1.1.

Т аблица 1.1

с d

€

с с

/ /

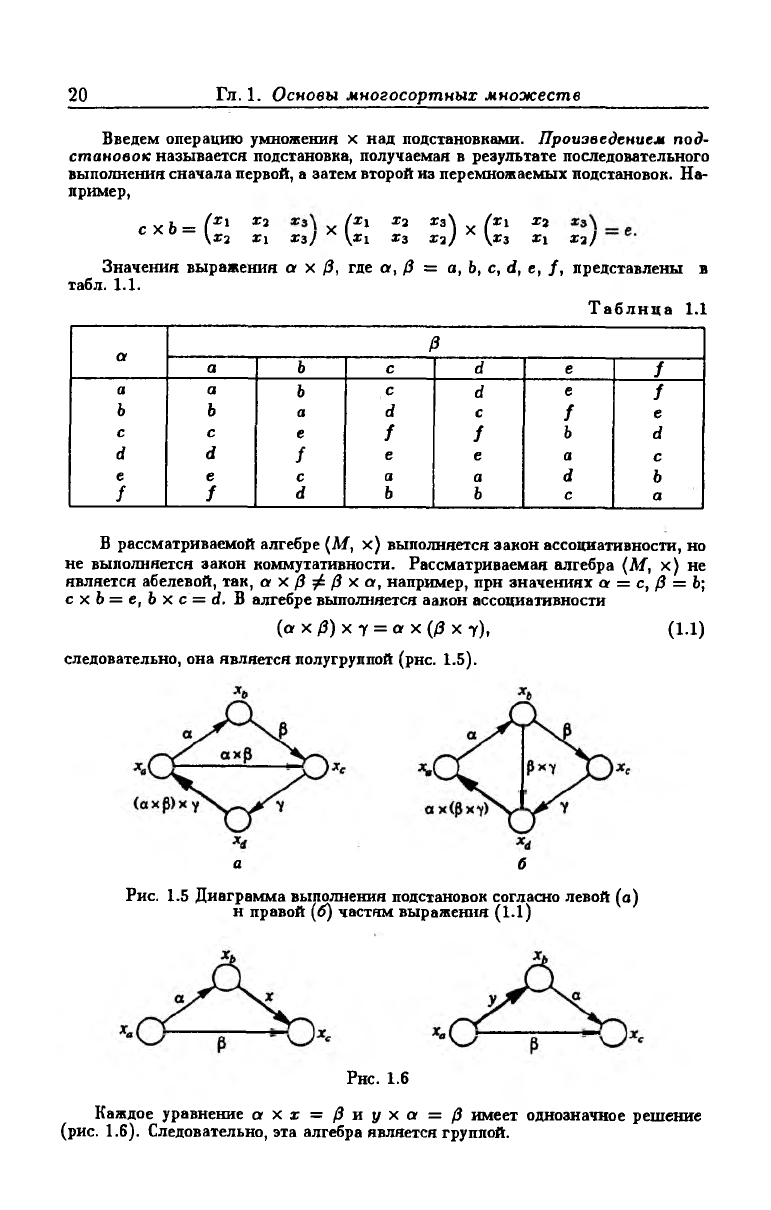
В рассматриваемой алгебре {М, х) выполняется закон ассоциативности, но

не выполняется закон коммутативности. Рассматриваемая алгебра (М, х) не

является абелевой, так, а х (3 ф (3 х а, например, прн значениях а = с, /3 = Ь;

с х Ь = е, Ь х с = d. В алгебре выполняется аакон ассоциативности

(а х /3) х у = а х (/? х у), (1.1)

следовательно, она является полугруппой (рнс. 1.5).

а б

Рис. 1.5 Диаграмма выполнения подстановок согласно левой (а)

н правой (б) частям выражения (1.1)

Рнс. 1.6

Каждое уравнение а х х = / 3 и у х а = (3 имеет однозначное решение

(рис. 1.6). Следовательно, эта алгебра является группой.