Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§ 1.4. Решетка

свойство антисимметричности отношения < вытекает из закона

коммутативности:

771; < rrij & rrij < 771; f-> 771; = rtlj П 771; = 771; П 77lj = mj.

Если тп,- > mj & mj > m^, то согласно (1.3)

тп; П m*. = тп; П (mj П mjt) = (m; П mj) П m*. = rrij П mjt = m*,

откуда m,- > m*; в результате доказано свойство транзитивности

отношения <.

Наконец, согласно свойствам идемпотентности, коммутативно

сти и ассоциативности операции пересечения получаем

тп,- П (т,- П mj) = (т ; П т ,) П mj = т,- П mj,

и т ; П mj является нижней гранью для тп,-, а согласно (1.2) — и

для mj. Более того, т,- flmj есть наибольшая нижняя грань, так

как из т,- > mjt и rrij > rrik вытекает согласно (1.3)

(т ; П rrij) П т* = m; П (mj П m*) = m; fl m* = m*.

Согласно принципу двойственности m, Umj является наименьшей

верхней гранью для т,- и rrij.

В результате проведенного доказательства получена связь меж

ду определениями решетки как частично упорядоченного множе

ства и как алгебры с двумя операциями Пии, где U — операция

взятия наименьшей верхней грани элементов (объединения); П —

операция взятия наибольшей нижней грани элементов (пересече

ния).

В качестве упражнения вычислим значение некоторой формулы F, рассма

тривая решетку как алгебру. Имеем F(a, Ь) = (о П (о U Ь)) П ((о U (о П Ь)) П

n(oUb)) UOUo = оП(оП(ои6)) UOUo = (ono)UOUo = oUOUo = aUa = а.

При упрощении F(a, b) были использованы свойства (1.4), (1.2) и идемпо

тентность.

Здесь и ниже 0 и 1 в решетке будем называть структурными

нулем и единицей; при этом

(Vm,)(0 П тп; = О, О U m; = т ;, mi П 1 = т ;, т,- U 1 = 1).

Определим в решетке свойство дистрибутивности. Подрешет-

кой А решетки А называется подмножество решетки А, которое

вместе с каждой парой элементов m;, rrij из А содержит также

т,- U rrij и т,- П rrij. Интервалом J, определенным элементами

т а и тр в решетке А, называется подрешетка А' решетки А с

наибольшим элементом тр и наименьшим элементом т а:

J = [ т а, тр] = { т ; 6 А '/ т а < т ; < тр}.

В решетке А со структурными нулем и единицей два элемента,

тпа и тр, называются дополнительными, если

та П тр = 0, та U тр = 1.

Гл.1. Основы многосортных множеств

Элемент, дополнительный к m fin), называется также допол

нением элемента тп в решетке А. Два элемента, обладающие об

щим дополнением в решетке А, называются связанными в А.

Важным классом решеток являются дистрибутивные решетки.

Решетка А называется дистрибутивной, если она удовлетворяет

следующим тождествам:

(т,- U mj) Пгпк — т,- П т* U mj П т*,

т * П (т,- U rrij) = т*. П rrij U т * П rrij

для всех т,-, mj, т* 6 М.

Согласно свойству коммутативности пересечения для опреде

ления дистрибутивной решетки достаточно выполнения одного из

этих тождеств.

Критерий дистрибутивности решетки. Решетка

А дистрибутивна тогда и только тогда, когда в каждом ин

тервале J решетки А любые два связанных в J элемента равны.

Этот критерий можно выразить в более удобной для вычисле

ний форме, если найти структуру подрешеток, наличие которых

выводит решетку из класса дистрибутивных.

Введем понятие дедекиндовых (модулярных) решеток. Решет

ка А называется дедекиндовой тогда и только тогда, когда

(Vm,-, mj, mk € A, mj < m*) ((m,- U mj) n m* = mj Г) m* U m ,).

Критерий дедекиндовости решетки. Решетка А

дедекиндова тогда и только тогда, когда она не содержит

подрешетки, изоморфной решетке Ат (рис. 1.12, а).

Решетка Ат содержит один элемент нулевой высоты, два эле

мента единичной высоты и по одному элементу, высота которых

2 и 3.

Используя критерий модулярности решеток, сформулируем

критерий дистрибутивности в более удобной для вычислений фор

ме: решетка дистрибутивна

тогда и только тогда, когда

она не содержит подрешетки,

изоморфной Ат , т. е. является

дедекиндовой, и не содержит

подрешетки, изоморфной под-

решетке Ая (рис. 1.12,6). Ре

шетка Ад содержит три цепи

длины 2 , состоящие из одного

элемента нулевой высоты, трех

Рис. 1.12 элементов единичной высоты и

одного элемента высоты 2 .

Решетка А, задаваемая диаграммой Хассе Н (см. рис. 1.10,6),

является не только дедекиндовой, но и дистрибутивной.

$1.4. Решетка 33

В решетке А со структурными нулем и единицей, в которой

каждый элемент тп обладает дополнением тп, можно считать за

данной унарную одноместную операцию /i(m ) = тп. Решетка А

называется решеткой с дополнениями, если она обладает струк

турным нулем и такой унарной операцией /i(m ) = m, что

Согласно (1.5) и (1.6) одна из операций U, П может быть

выражена через другую. Следовательно, решетку с дополнениями

можно определить как алгебру, сигнатура которой состоит

из U, .

Отметим некоторые следствия тождеств (1.5)—(1.7). Имеем

О < тп для всех тп 6 М; следовательно, О П тп = 0.

Бели положить 1 = 0 , а 0 (1 т = 0 и 0 1 1 тп = тп подставить в

(1.6), то получим 1 Птп = тп, 1 U тп = 1 . Следовательно, 1 — наи

больший элемент решетки, т. е. является структурной единицей.

Согласно тождествам (1.7) и (1.6) тп1)тп= 1.

Дистрибутивная решетка с дополнениями называется булевой

алгеброй.

Изоморфизмом г) между алгебрами А\ = (Mi, Si) и =

= (М2 , S2) называется такое взаимно однозначное соответствие

между элементами носителей и сигнатур, что

/,(тпв1, тп0з, ..., тп0(к_1) = т ак <->

<-> *?(/.)Ы™»,), т?(тв2), •••) *?("*<»*_,)) = T)imak),

тву € M i, v(maj) € М2, j = 1, 2 , ..., А, /, € Si, ??(/,■) € S2.

Алгебры, между которыми существует изоморфизм, называ

ются изоморфными. Все законы алгебры Ai справедливы и в

изоморфной ей алгебре А2.

Теорема 1.2 (Стоун). Булева алгебра изоморфна алгебре

Кантора.

Для рассматриваемых алгебр имеется следующий изоморфизм:

o U 6 «+Ma UMb, аПЬ ++ МаПМь, а <-> Ма,

где в левых частях выражений стоят теоретико-решетчатые, в пра

вых — теоретико-множественные операции. Эти операции имеют

одно и то же написание, поэтому, чтобы их различать, аргументы

теоретико-решетчатых операций будем обозначать малыми бук

вами, а аргументы теоретико-множественных операций — боль

шими буквами латинского алфавита.

т{ U mj ±= тп,- П mj,

mflm = 0.

т = т,

(1.5)

(1.6)

(1.7)

2 В. А. Горбатов

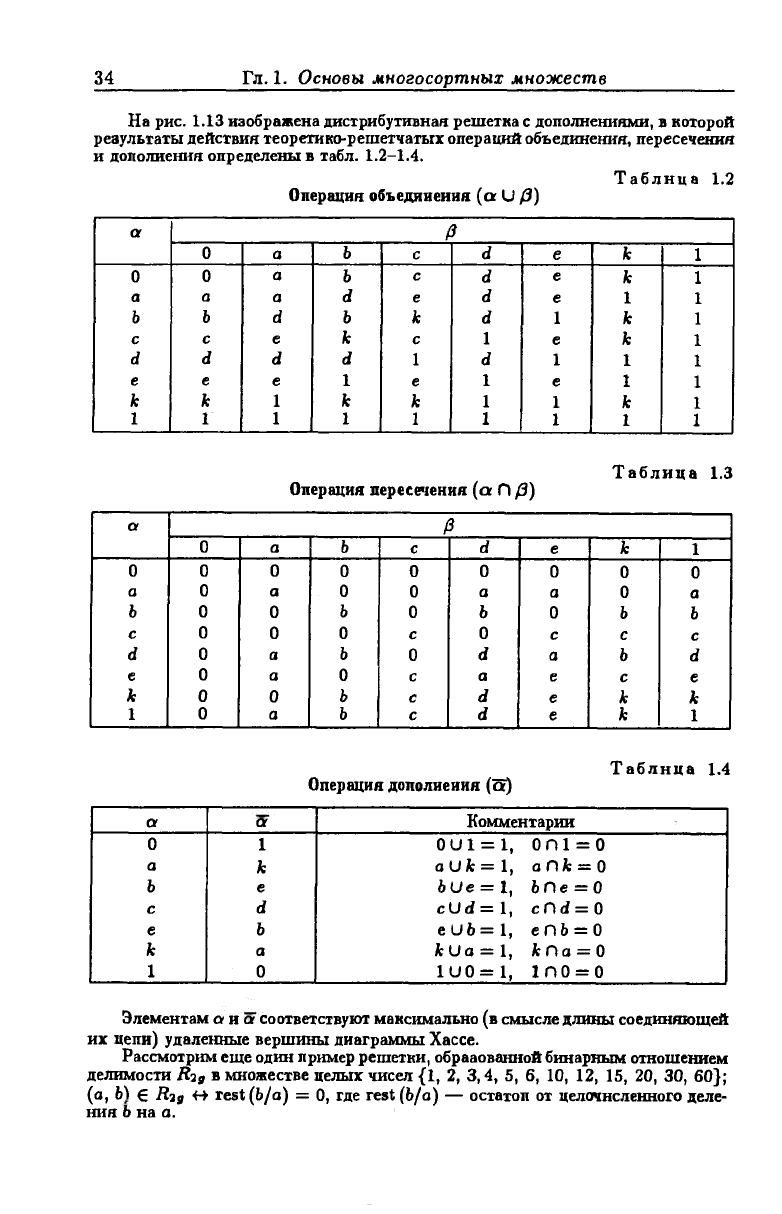
34 Гл. 1. Основы многосортных множеств

На рис. 1.13 изображена дистрибутивная решетка с дополнениями, л которой

результаты действия теоретико-решетчатых операций объединения, пересечения

и дополнения определены в табл. 1.2-1.4.

Т абли ца 1.2

Операция объединения (a U /3)

с d

e к

а а

а d е d

Ь d

к d 1

с е к

с 1

e к

d d

1 d 1

е 1

к к 1 к

к 1

1 1 1 1

1 1

Т абли ца 1.3

Операция пересечения (а П /3)

а Ь

е к

0 0 0

0 а

а 0

Ь 0 Ъ

0 0

с с

d 0

а 0

с е

к 0

0 Ь

к к

а Ь

с d е к

Т абли ца 1.4

Операция дополнения (5)

Комментарии

1 0 U 1 = 1,

0П1 = 0

a U к = 1,

аП к = 0

Ь е bUe = 1,

ЬПе = 0

cU d = 1,

с П d = 0

е Ъ

е U 6 = 1, еПЬ = 0

к а

kU a = 1,

к П а = 0

1 0 1 U 0 = 1, 1 ПО = 0

Элементам о н а соответствуют максимально (в смысле длины соединяющей

их цепи) удаленные вершины диаграммы Хассе.

Рассмотрим еще один пример решетки, образованной бинарным отношением

делимости Rig в множестве целых чисел {1, 2, 3,4, 5, 6, 10, 12, 15, 20, 30, 60};

(о, Ь) € Rig <-»■ rest (Ь/о) = 0, где rest (Ь/а) — остатоп от целочисленного деле

ния Ь на а.

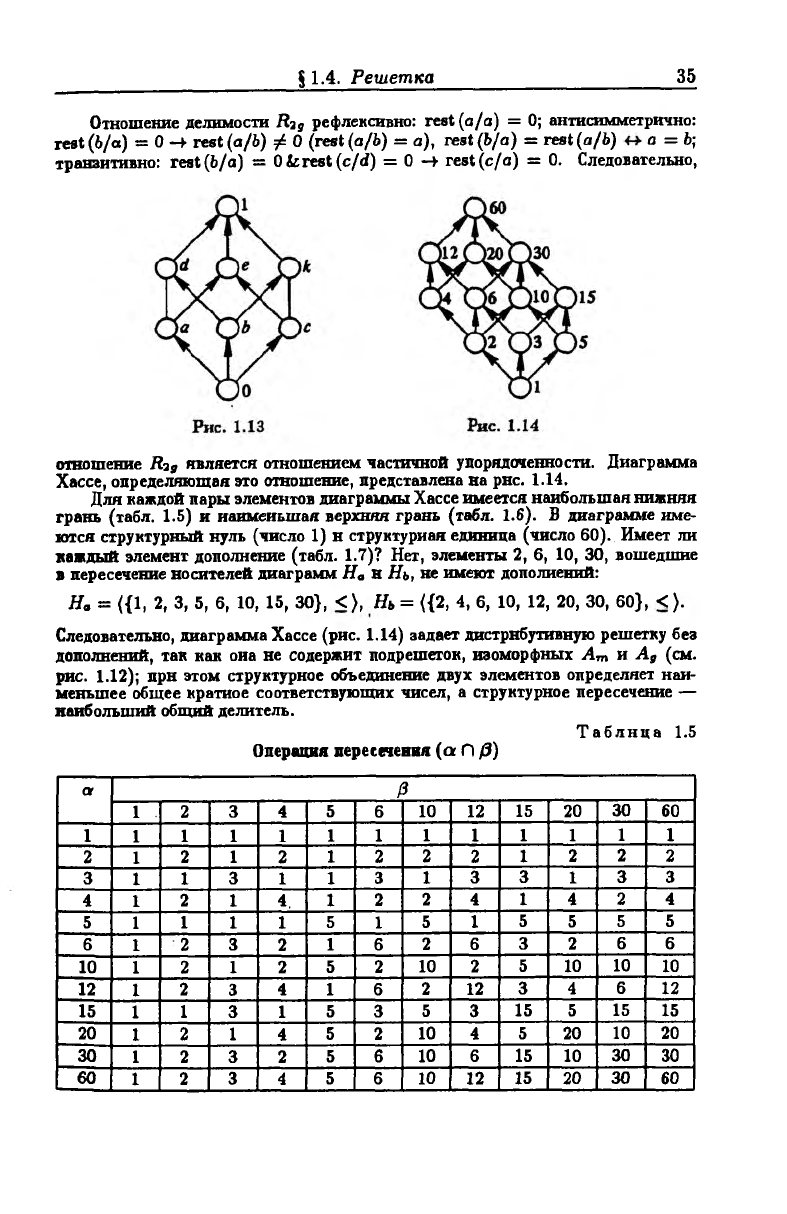
§1.4. Решетка

Отношение делимости R ig рефлексивно: rest (а/а) = 0; антисимметрично:

rest (6/а) = 0 —► rest (а/Ь) / 0 (rest (а/Ь) = a), rest (Ь/а) = rest (а/Ь) а = Ъ\

транзитивно: rest (Ь/а) = 0 1 rest (c/d) = 0 —¥ rest (с/а) = 0. Следовательно,

отношение R?a является отношением частичной упорядоченности. Диаграмма

Хассе, определяющая это отношение, представлена на рнс. 1.14.

Для каждой пары элементов диаграммы Хассе имеется наибольшая нижняя

грань (табл. 1.5) и наименьшая верхняя грань (габл. 1.6). В диаграмме име

ются структурный нуль (число 1) н структурная единица (число 60). Имеет ли

каждый элемент дополнение (табл. 1.7)? Нет, элементы 2, 6, 10, 30, вошедшие

В пересечение носителей диаграмм На н Нь, не имеют дополнений:

На = ({1, 2, 3, 5, 6, 10, 15, 30}, <>, Нь = {{2, 4, 6, 10, 12, 20, 30, 60}, < ).

Следовательно, диаграмма Хассе (рис. 1.14) задает дистрибутивную решетку без

дополнений, так как оиа не содержит подрешеток, изоморфных А т и А я (см.

рис. 1.12); прн этом структурное объединение двух элементов определяет наи

меньшее общее кратное соответствующих чисел, а структурное пересечение —

наибольший общий делитель.

Т аблица 1.5

Операция пересечения (а П /3)

15 20

1 1 1

1 1

2 1

1 2

3 1 1

3 1

3 3

4 1

1 4.

2 4 1 4

2 4

1 1

5 1

5 5

1 2

1 6

2 6

3 2

6 6

1 2

5 2

10 2

5 10

3 4

1 6

2 12

3 4

1 3 1

5 3

15 5

2 1

5 2

5 20

10 20

1 2 3 2

5 6

10 6 15 10

2 3 4

5 6

15 20 30 60

Гл. 1. Основы многосортных множеств

Т аблица 1.6

Операция объединения (a U /3)

10 12

20 30

1 1

3 4 5

10 12 15 20

2 2 2

10 6 10

12 30

20 30

6 '

6 30

60 30

4 4

12 4 20

20 12 60 20 60

5 5

15 20

20 30

6 6

30 60 30

10 10 10

20 10

10 60 30 20 30

12 60

60 60 60

15 15

60 15

30 60

15 60 30

20 20

20 60 60 20 60

30 30

60 30

30 60 30 60 30

60 60 60 60 60 60 60 60 60

Т абли ца 1.7

Операция дополнения (а)

3 4

10 12

20 30

а 60

нет

Если после замены дуг на цепи соответствующей длины диа

грамма Хассе На преобразуется в диаграмму, изоморфную диа

грамме Нь, то диаграммы На и Щ называ

ются гомеоморфными.

Теорема 1.3. Диаграмма Хассе Н

не определяет решетку, если она содер

жит поддиаграмму, гомеоморфную Н3

Рис. 1.15 (РИС. 1.15).

Доказательство. Очевидно, что эле

менты а и /3 не имеют наибольшей нижней грани, элементы у и

S — наименьшей верхней грани.

§ 1.5. Модель. Алгебра отношений

Аналогично бинарному отношению определим n-арное отно

шение.

Декартово произведение п равных между собой множеств М

называется n-й степенью М п множества М . Под п-арнъш от

ношением Т в множестве М понимается подмножество Т его п-й

степени Т С М п. Если элементы mtl, тп,-2, ..., m,in принадлежат

М и (mtl, тп{2, m,n) 6 Г, то говорят, что элементы находятся

в отношении Т. Любое n-арное отношение может быть задано в

виде списка, элементами которого являются последовательности

§1.5. Модель. Алгебра отношений

(кортежи), определяемые этим отношением. Рассмотрим свойство

симметричности n-арных отношений, позволяющее эффективно

использовать n-арные отношения при формализации многих прак

тических задач. Симметричным называется n-арное отношение

Т в множестве М такое, что если (mtl, т,-2, ..., тп,п) 6 Т, то

и любая последовательность (mjx, mj2, ..., mjn), полученная из

(тп,-,, гп;2 , ..., т , п) перестановкой элементов, также находится в

отношении Т: (тп^, т ,2, ..., mjn) € Т.

По существу n-арное отношение, обладающее свойством сим

метричности, задает подмножества, которые состоят из п элемен

тов, — подмножества мощности п. В дальнейшем n-арное отно

шение, обладающее свойством симметричности, будем называть

S-ричным отношением (5-отношением или словесным отноше

нием). Элементы множества М , в котором определено 5-отно

шение, будем называть буквами, а подмножества, определяемые

5 -отношением, будем называть словами и обозначать /х,-.

Задавать 5-отношение можно более удобными способами: ма

трицей инцидентности и модельным графом (мографом).

Матрицей инцидентности Q = [gtJ] называется двумерная

матрица, каждому столбцу которой взаимно однозначно соответ

ствует буква, строке — слово, определяемое 5-отношением, и

Например, 3-отношение в множестве М = {а, и, о, р, с, ы}, определяющее

СЛОЛа Цх = { с, О, р}, = {р , «1 с } , цз = {с, ы, р } , щ — {о, с, о } , с помощью

Матрицы инцидентности Q можно аадать следующим образом:

Если отношение 5 определяет подмножество М ', М ' С М*, то

число s будем называть степенью отношения S.

Задать 5-отношение произвольной степени с помощью графа,

носитель которого совпадает с множеством букв, нельзя (см. тео

рему 1.4).

Граф называется полным, если все его вершины попарно

смежны.

Теорема 1.4. Если хотя бы три различных слова, опреде

ляемые отношением 5, соответствуют полному подграфу гра

фа G , то граф G не задает отношение S.

Доказательство. При задании словесного отношения гра

фом будем ассоциировать определяемое слово с полным подгра

фом графа G. Тогда теорема очевидна. Действительно, достаточно

а и о р с ы

0 0 1 1 1 0

Q = 0 1 0 1 1 0

0 0 0 1 1 1

1 0 1 0 1 0

Гл.1. Основы многосортных множеств

рассмотреть следующий пример. Пусть 3-отношение в множестве

М = {в, тп, о, р} определяет слова = {т, о, р}, = {р, о, в},

ц3 = {в, m, о}, которым соответствует граф (7, изображенный на

рис. 1.16, а. Это полный граф на четырех вершинах. Он может за-

Рис. 1.16

давать слово {в, тп, о, р} или слова {тп, о, р}, {р, о, в}, {в, о, тп},

или слова {тп, о}, {р, о}, {тп, р}, {в, р}, {тп, в}, {в, о}, т. е. имеет

место неоднозначность.

Для однозначного задания словесных отношений необходимо

каждой букве (вершине) сопоставить множество идентификаторов

слов, в которые эта буква входит. Тогда всякому слову взаимно

однозначно соответствует полный подграф, каждой вершине ко

торого соответствует идентификатор этого слова. Такой полный

подграф, соответствующий слову, в дальнейшем будем называть

элементным. Процесс сопоставления каждой букве множества

идентификаторов слов, в которые эта буква входит, будем называть

моделизацией графа G. В результате моделизации графа G ка

ждой вершине взаимно однозначно соответствует буква, взвешен

ная множеством идентификаторов слов, в которые она входит; при

этом две вершины смежны (соединены линией без ориентации —

ребром), если им соответствует хотя бы один общий идентифи

катор. Полученную таким образом на графе функцию, областью

определения которой являются вершины графа, а областью значе

ний — множества идентификаторов слов, будем называть

модель

ным графом (мографом) и обозначать GM — ((V, W ), U). Здесь

W — множество идентификаторов слов.

Мографы Gj* и G^f, задающие соответственно отношения Si = {{m, о, р},

{р, о, в}, {в, о, т} } в множестве Mi = {в, т, о, р} и = {{с, о, р),

{р, и, с}, {с, ы, р}, {о, с, о}} в множестве Afj = {о, и, о, р, с, ы}, изображены

2 3 4

на рис. 1.16, б, 1.17, а.

Для задания 5-отношений используют также термин гипер

граф. При геометрической интерпретации гиперграфа его буквы

взаимно однозначно сопоставляются вершинам, слова — кругам

§ 1.5. Модель. Алгебра отношений

Эйлера, которые охватывают буквы, входящие в соответствующее

слово.

Геометрическая интерпретация гиперграфа, определяющая совокупность

{М, S3), где

М = {о, и, о, р, с, ы}, S3 = {{с, о, р), {р, и, с}, {с, ы, р}, {о, с, о}},

изображена иа рис. 1.17, б.

Однозначно задать 5-отношение с помощью графа можно, если

в качестве носителя графа взять не только множество букв, но

/>Ц,2,3)о(1,4)

Рис. 1.17

и множество идентификаторов слов. Такое задание 5-отношения

осуществляется двудольным графом.

Граф G = (V, U) называется двудольным (простым или гра

фом Кёнига), если его носитель разбит на два подмножества, V +

и V~, не имеющих общих вершин, и начало каждой дуги и € U

принадлежит подмножеству V +, и только ему, а конец — подмно

жеству V” , и только ему. При задании 5-отношений элементам

подмножества V + в двудольном графе G = (V, U) взаимно одно

значно сопоставляют буквы, элементам подмножества V- — иден

тификаторы слов и (va, vp) € U, если и только если вершина va

соответствует букве, входящей в слово

vp.

Двудольный граф, задаю

щий 3-отношение S3 = {{с, о, р}, {р, и, с), {с, ы, p j, {о, с, а}} в

1 2 3 4

множестве {а, и, о, р, с, }, изображен на рис. 1.17, в.

Одним из основных в дискретной математике является поня

тие модели. Моделью Ф называется совокупность множества М с

заданными в нем отношениями

5 = {Лц, R12, .. •, Rim,R2i, R 22, • • •) Й2п2, • • •

. . ., Rm 1) Rm2, • • •) Rmnm}j

где множество M — носитель модели, а заданные отношения

Д,а, Ria С М ’ образуют сигнатуру модели Ф = (М, 5).

Гл. 1. Основы многосортных множеств

Степень носителя определяет арность отношения. Два от

ношения R a и Rp, имеющие одну и ту же степень, называются

совместимыми по объединению или просто совместимыми.

Очевидно, что n-местную операцию / n(mi, m2, ..., т п) =

= m„+i можно рассматривать как (п+ 1)-арное отношение Rn+i-

Совокупность множества М с заданными в нем операциями и

отношениями, следуя А.И. Мальцеву, будем называть алгебраиче

ской системой.

Частным случаем алгебраической системы является алгебра

отношений и ее расширение — реляционная алгебра.

Рассмотрим алгебру отношений, носитель которой — множе

ство отношений, а сигнатура — операции объединения, пересе

чения, разности и расширенного декартова произведения отно

шений.

Объединением R a U Rp двух совместимых отношений R a и

Rp является множество всех кортежей, каждый из которых при

надлежит хотя бы одному из этих отношений. Объединение отно

шений

Ra = {(о,

ь,

с), (а, Ь, d), (Ь, с, е)}

Rp = {(а, 6, d), (Ь, d, е), (с, d, е)}

есть

RaURp = {(а, Ь, с), (а, Ь, d), (6, с, е), (6, d, е), (с, d, е)}.

Рассмотренные отношения R a и Rp являются совместимыми,

так как их степени равны: s(Ra) = s(Rb) = 3, R a, Rb С M 3, М =

= {о, Ь, с, d, е}.

Пересечением Ra П Rp двух совместимых отношений Ra и

Rp является множество всех кортежей, принадлежащих как отно

шению R a, так и отношению Rp. Пересечение отношений Ra и

Rp для рассматриваемого примера есть

R a П Rp = {(а, Ь, с), (а, b, d), (6, с, е)} П

Г) {(а, 6, d), (6, d, е), (с, d, е)} = {(а, 6, d)}.

Разностью R a \ Rp двух совместных отношений Ra и Rp

является множество всех кортежей, принадлежащих отношению

R a и не принадлежащих отношению Rp; для данного примера

Ra \ Щ =

= {(о, Ь, с), (а, Ь, d), (6, с, е)} \ {(а, 6, d), (6, d, е), (с, d, е)} =

= {(а, Ь, с), (6, с, е)}.

Расширенным декартовым произведением R a х Rp двух от

ношений R a и Rp является множество всех кортежей п таких, что