Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика
Подождите немного. Документ загружается.


§1.9. Нечеткие подмножества
81
Сигнатура векторной решетки удовлетворяет законам:
коммутативности
А х В = В х А, А + В = В + А;
ассоциативности
А х (В х С) = (А х В) х С,
А + (В + С) = (А + В) + С;
действия с константами
А х 0 = 0 , А + 0 = А, А х 1 = А.
Расширим сигнатуру введенной алгебры унарной операцией до
полнения, определенной в начале этого параграфа (дополнением,
определяемым свойством нечеткости подмножества; не путать с
дополнением, определенным в § 1.4). Тогда к перечисленным за
конам добавляются еще два:
закон инволюции _
А = А;
законы де Моргана
А х В = А + В, А + В = А х В.
Докажем законы де Моргана. Пусть да (я) = а, цв{%) — Ь;
тогда
1-аЬ={1 -а) + (1-Ь )-{1- а) (1 - Ъ) =
= 1 — о+ 1 — 6 — 1 + а + Ь—а-6 = 1 — а-6;
1 — (а + b — ab) = (1 — а) • (1 — b) = 1 — а — b + ab.
Законы дистрибутивности в векторной решетке не выполня
ются. Действительно, рассмотрим закон дистрибутивности
Ах(В + С) = АхВ + АхС.
Для левой части соотношения имеем
а • (Ь+ с — Ъс) = аЬ + ас — abc,
а для правой —
ab + ас - (ab) • (ас) = ab + ac — а2Ьс, с = цс{х)-
Следовательно, закон дистрибутивности не выполняется, если
о2 ф а.
Для операций алгебраического произведения х и алгебраиче-
ской суммы + также не выполняются закон идемпотентности и
соотношения, аналогичные (1.9):
А х А ^ 0, А + А^1.
82
Гл. 1. Основы многосортных множеств
• •
Связь между операциями х и + и операциями пересечения П
и объединения U устанавливают законы:
А х (В ПС) = (А х В) П (А х С),
А х (В U С) = (А х В) U (А х С),
А+(ВПС) = (А + В)П(А + С),
A+(BUC) = (A + B)U(A + C).
Докажем, например, последний закон. Пусть
цА(х) - а, цв{х) = Ь, цс(х) = с;
тогда левая часть соотношения имеет вид
а + шах(Ь, с) - а - тах(Ь, с),
правая —
тах(а + Ъ — ab, а + с — ас).
При Ь > с слева получаем о + b — ab, справа (учитывая, что
а < 1) также a, + b — ab. Аналогичный результат имеем и при
Ь < с.
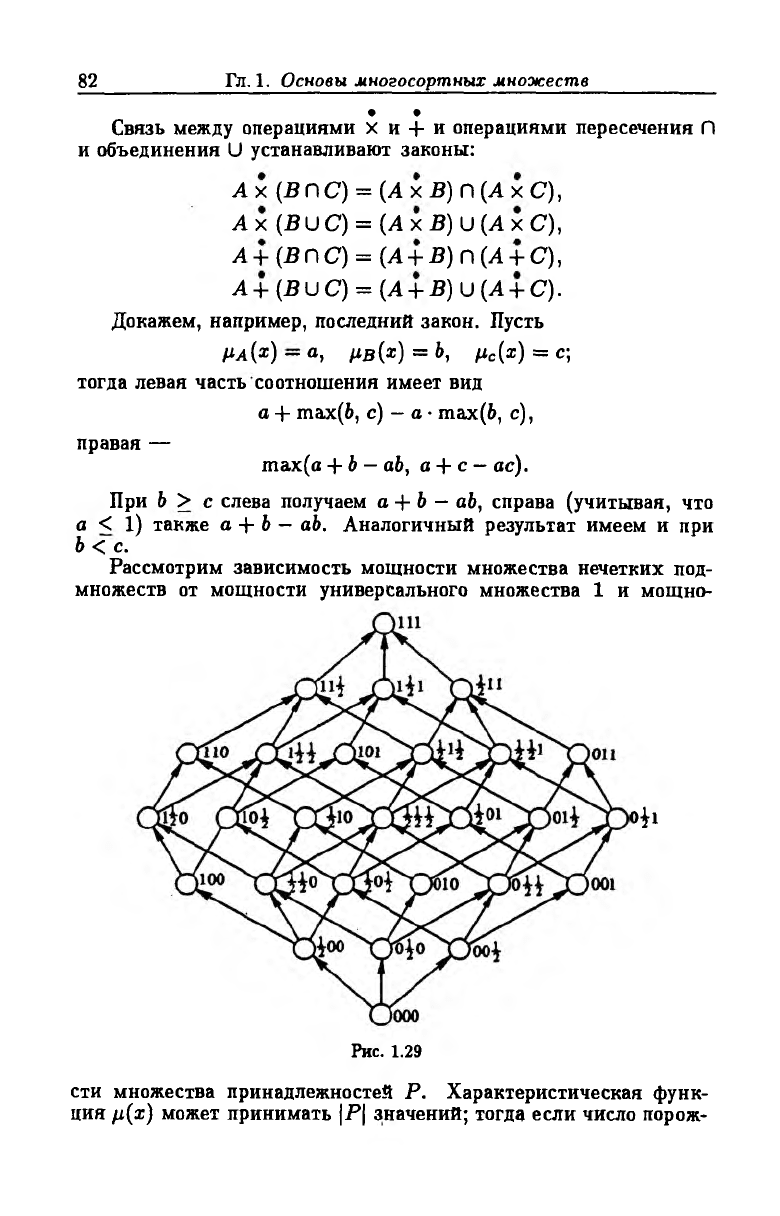
Рассмотрим зависимость мощности множества нечетких под
множеств от мощности универсального множества 1 и мощно-
0^1
Рис. 1.29
сти множества принадлежностей Р. Характеристическая функ
ция ц(х) может принимать \Р\ значений; тогда если число порож-

§1.10. Метрические пространства
83
дающих множеств (размерность универсума) равно п, то мощ
ность множества нечетких подмножеств |5(1)| имеет вид
I■5(1)1 = 1ЛП-
На рис. 1.29 представлена векторная рещетка, соответствую
щая универсальному множеству 1 (Mi, М2, Мз) размерности 3 и
множеству принадлежностей Р = {0; 0.5; 1}. Векторная решетка
определена диаграммой Хассе, в которой каждой вершине Vi соот
ветствует вектор Х{\
ЦмЛх) ММ2(г) Ш3(х)
и (va, щ) — дуга, если Х а < Хь\ при этом
Ха ^ Хь (Vxaj, Xbf)(xaj К Xft;).
Еак было оговорено раньше, в диаграмме Хассе по сравнению
с графом, определяющим отношение упорядоченности, не указы
ваются петли и транзитивно замыкающие дуги.
§ 1.10. Метрические пространства
Некоторые задачи информационной математики сводятся к
определению “близости” нечеткого подмножества к подмножеству,
выполняющему роль эталона (образца). При решении этих задач,
как правило, используется понятие метрического пространства.
Метрическим пространством называется многосортное мно
жество (М, D), состоящее из элементов множества М (точек) и
определенного в нем расстояния d(rrii, mj) £ D между любыми дву
мя точками m,-, mj £ М, удовлетворяющего условиям:
неотрицательности
,, \ Г = 0, если mi = тп,-,
d(mi,mj){ > 0 ; если гщфт]-
симметричности
d(mi, m j) = d(rrij, тп,-);
транзитивности
d(mit rrij) + d(mj, mk) > d(m,-, m*).
Введем широко используемые понятия “расстояния”.
Рассмотрим детерминированные (обычные) подмножества в
пространстве 1. Расстоянием Хемминга dh(A, В) между подмно-
П
жествами А, В С 1 называется число, равное |мл(а:«)~мв(х^)|,
«=1
где п — размерность пространства.

84
Гл. 1. Основы многосортных множеств
П ри м ер 1.15. А, В С l(M j, Мз, Мз, Mi, Ms),
А
1
0
1 1
0
В 0 1 1 0
1
dh(A, В) = |1 - 0| + |0 - 1| + |1 - 1| + |1 - 0| + |0 - 1| = 4.
Расстояние Хемминга показывает количество разрядов, в кото
рых соответствующие векторы отличаются.
Относительным расстоянием Хемминга dh0(A, В) между
подмножествами А, В С 1 называется число, равное п-1 •dh(A, В),
где п — размерность пространства 1.
Для примера 1.15 dho(A, В ) = 5-1 • 4 = 0.8. Очевидно, что
0 < dho(A, В )< 1.
Обобщим понятие “расстояние Хемминга” для нечетких под
множеств.
Обобщенное расстояние Хемминга (линейное расстояние)
dj,(A, В) между нечеткими подмножествами А, В С 1 определя-
П
ется значением |ца{%{) - Мв(я«)|, где п — размерность про-
1=1
странства.
П ри м ер 1.16. А, В С l(M i, Мг, .. Me),
А
0.2 0.8
1.0 0.0 0.7 0.8
В 0.3
0.9 0.8 0.6
1.0
0.0
d*(A, В) = |0.2 - 0.3| + |0.8 - 0.9| + |1.0 - 0.8| + |0.0 - 0.6| +
+ |0.7 - 1.0| + J0.8 - 0.0| = 2.1.
Относительное линейное расстояние d ^ A , В) определяется
как
dOJI(A, В) = п -1 • dn(A, В).
Для примера 1.16 d ^ A , В) = 6 1 • 2.1 = 0.35. Очевидно, что
0 < dOJI(A, В) < 1.
Евклидовым (квадратным) расстоянием de(A, В) между не
четкими подмножествами А, В С 1 называется число
\
- м в ( * Л ) 2 ,
«=1
где п — размерность пространства 1.
Очевидно, что 0 < de(A, В) < у/п.
Относительное евклидово расстояние deo(A, В) определя
ется как
dto(A, В )= (^п )_1 ч*,(А, В).

§ 1.10. Метрические пространства
85
Очевидно, что 0 < deo(A, В) < 1.
П рим ер 1.17. Вычислим dt(A, В) и d,a(A, В) для нечетких подмножеств,
заданных в примере 1.16:
d'(A, В) - V 0.12 + 0.12 + 0.22 + 0.62 + 0.32 + 0.82 = а/1Л5 « 1.07,
d,o(A, В)=. 6-1 1,07 « 0 .1 8 .
Легко показать что детерминированное подмножество А явля
ется ближайшим в смысле наименьшего значения евклидова рас
стояния от нечеткого подмножества А' при характеристической
функции
„ , ЛгЛ - I 1’ еслия4/(хЛ > 0.5,
РА\ г) |0 , если Дд'(х,) < 0.5.
П рим ер 1.18. Пусть иечеткое подмножество А' имеет вид
А'
0.2 0.8
0.4 0.5 0.6 0.9
тогда ближайшим детерминированным подмножеством будет
m
о
Рассмотрим еще два определения “расстояния” — линейный
индекс нечеткости А (А'), вычисляемый через относительное ли
нейное расстояние don{A', А), и квадратичный индекс нечетко
сти х(А'), определяемый посредством относительного евклидова
расстояния deo(A', А):
А(А') = 2 • (п)-1 • ^ГОмл'О1.) ~ Мл(*,-)|),
«=1
Х(А') = 2 • (Vn) 1
\
i=1
где n — размерность пространства.
Коэффициент 2 в выражениях проставлен для того, чтобы вы
полнялось
О < А(А') < 1 , 0 < х(А') < 1,
так как относительное линейное расстояние
dOJt(A', А) и относи
тельное евклидово расстояние deo(A', А) принимают значения на
отрезке [0; 0.5].
, П рим ер 1.19. Вычислим линейный и квадратичный индексы нечеткости
подмножества А':
А!
0.1
0.8 1.0 0.6
0.5

86
Гл. 1. Основы многосортных множеств
Нечеткое подмножество А' определяет ближайшее детерминированное под
множество А:
EU
Отсюда получаем линейный и квадратичный индексы нечеткости:
Л(А') = 2 • (5)-1 ■ (J0.1 - 0.0| + )0.8 - 1.0| +
+ 11.0 - 1.0| + |0.6 - 1.0| + |0.5 - 0.0|) = 2 • 5-1 • 1.2 = 0.48,
Х(А') = 2 • (V 5)-1 • >/046 » 0.63.
Применение операций в алгебре нечетких множеств изменяет индекс нечеткости
случайным образом.
§ 1.11. Задачи и упражнения
1.1. Доказать, что
А с В * + А и В = В *+ АпВ — А * + А \В = 0 <+АиВ = 1 .
1.2. Доказать, что
ЛП(В\А) = и, Л\(ВиС) + (Л\В)\С.
1.3. Решить систему уравнений
А \ Х = В, А и Х = С,
где А, В, С — заданные множества и В С А С С.
1.4. Доказать, что А = В (А \ В) U (В \ А) = йг.
1.5. Доказать, что если отношения Ri и Яг рефлексивны, то рефлексивны
и отношения Ri U Яг, Hi П Яг.
1.6. Доказать, что если отношения Ri и Яг симметричны, то симметричны
и отношения Я 1 U Яг, Ri П Яг.
1.7. Доказать, что конечное множество мощности п содержит п!/(р!(п — р)!)
различных подмножеств мощности р < п.
1.8. Доказать, что U М; — наименьшее множество, содержащее все множе-
i
ства Mi.
1.9. Доказать, что О Mi — наибольшее множество, содержащееся во всех
i
множествах Mi.
1.10. Доказать, что если М0, Мь, М с и Мл не пусты, то:
а) М0 С Мь и Мс С Ма <■+ Ма х Мс С М ь х Мл;
б) Ма ~ Мь и М с — Мл Ма X М с = Mb X Мл-
п п п
1.11. Доказать, ЧТО О Ма: X П М(>: = П (М „; X МьЛ.
1 = 1 i=l i=l
1.12. Доказать, что
{Ма X Mb) и (Мс X М л) С (Ма и Мс) X (Мь и Md).
Установить, в каком случае в этой формуле имеется равенство.
1.13. Доказать, что:
а) (Мв и М ь) х Мс = (М0 х Мс) и (Мь х Мс);
б) Ма X (Мь U Мс) = (Ма X Мь) U (Ма х Мс);
в) (М„иМ ь) х (McuMd) — (M exM c)u(M bxM c)u (M e xM d)u(M bxM d);

§ 1.11. Задачи и упражнения
87
г) U М«( х 0 Мы = . П (M ei х Mbi);
•si i*l ij*l,...,n
д) П Mat х П Мы = П (Mai х Мы)-
• ж1 >sl l,J=l,...,n
1.14. Построить бинарное отношение:
а) рефлексивное, симметричное, иетранзитивное;
б) рефлексивное, транзитивное, несимметричное;
в) иерефлекснвиое, антисимметричное, иетранзитивное.
1.15. Какие из следующих отношений являются однозначными, какие обрат
но однозначными и какие взаимно однозначными:
(я, у) € Я у есть отец х,
(х, у) € Я у есть сын х,
(х, у) € Я х = у3,
(х, у) € Я <-*■ х* = у,
(х, у) € Я jx + 5j > (3 - у|?
1.16. Найти число всевозможных антисимметричных бинарных отношений
между элементами конечного множества, состоящего из п элементов.
1.17. Пусть М — множество всех параллелограммов иа плоскости, Ai —
множество квадратов, At — множество прямоугольников, Аз — множество ром
бов на плоскости. Найти результаты следующих операций:
Ai U Aj, Ai П Aj, Ai О Aj, i, j — 1, 2, 3.
1.18. Доказать, что два множества равны тогда и только тогда, когда резуль
таты их пересечения и объединения совпадают.
1.19. Известно, что из 100 студентов живописью увлекаются 28, спортом
42, музыкой 30, живописью и спортом 10, живописью и музыкой 8, спортом и
музыкой 5, живописью, спортом и музыкой 3. Определить:
а) количество студентов, увлекающихся только спортом;
б) ничем ие увлекающихся.
1.20. Установить, образует ли группу алгебра с носителем {0, 1,2,..., р— 1}
и сигнатурой — операцией сложения по модулю р.
1.21. Выяснить, образует ли группу алгебрз с носителем {0, 1, 2, ..., у — 1}
и сигнатурой — операцией умножения по модулю р.
1.22. Является ли полем алгебра с носителем {0, 1, 2, ..., р — 1} и сигнату
рой — оперзциями сложения и умножения по модулю р?
1.23. Показать, что отношение < в множестве целых чисел от 1 до к можно
задать треугольной матрицей смежности.
1.24. Доказать, что любое подмножество частично упорядоченного множе
ства имеет не более одной верхней и одной нижней грани.
1.25. Для множества двоичных векторов длины 4 построить граф, задающий
отношение
Ха < Хь (Vjce i , П,()(5С в( < Xbi)-
Выяснить, задает ли этот граф алгебру, если да, то установить результат опера
ций умножения и сложения.
1.26. Обозначим через
{Ма X Mb, р) = Ra х Rb, Ra = {Ма, < ), Rb = {Mb, < ),
множество, для которого
(я*вп ты)р(тац ты) m ej < < т ь (.
Показать, что:

88
Гл. 1. Основы многосортных множеств
а) Ra х Яь — частично упорядоченное множество;
б) Ra х Rb является цепью только в том случае, если Ra или Яь состоит из
одного элемента.
1.27. Доказать, что любая цепь является дистрибутивной решеткой.
1.28. Интервал [а, Ь] в частично упорядоченном множестве состоит из всех
элементов х, удовлетворяющих условию а < х <Ь. Доказать, что:
а) сечение двух интервалов является интервалом (быть может, пустым);
б) любой интервал в решетке является подрешеткой.
1.29. Рассмотрим объединение множеств взаимно простых чисел М и мно
жества всех произведений, сомножителями которых являются элементы множе
ства М; определим сложение и умножение в этом объединении как вычисление
наименьшего общего кратного и наибольшего общего делителя соответственно.
Установить, является ли совокупность объединения рассмотренных множеств и
операций сложения и умножения булевой алгеброй.
1.30. Доказать, что в любом коммутативном кольце
1.32. Рассмотрев совокупность (М, 0, + , х), где 0 + 0 = 0и0х0 = 0,
выяснить, является ли она: кольцом; телом; полем.
1.33. Доказать, что минимальное число цепей в представлении конечного
частично упорядоченного множества в виде суммы цепей равно максимальному
числу попарно несравнимых элементов.
1.34. Доказать, что в каждой решетке:
а) (а < Ь)&( с < d )—VaUc<bUd;
б) (а < Ь)&(с < Ь) -V a U с < Ь;
в) (а < ь\ —► (Vc)(a U с) < (bUс);
г) (а < Ь)й(с < d) -+ аПс <bnd\
д) (а < Ь)к(а <с) -¥ а <ЬГ\с-
е) (а < Ь) -V (Vc)(a Л с) < (Ь Л с).
1.35. Доказать, что в каждой решетке для любых элементов а, Ь, с:
а) a U Ь П с < (a U Ь) Г) (a U с);
б) а п (Ь и с) > а п 6 и а п с;
B )a< b-> aU b nc< (aU c)nb .
1.36. Доказать, что решетка модулярна тогда и только тогда, когда для
любых трех элементов а, Ь, с
1.37. Доказать, что решетка дистрибутивна тогда и только тогда, когда для
любых трех элементов а, Ь, с
1.38. Найти множество “запрещенных фигур”, выводящее частично упоря
доченное множество из класса решеток.
1.39. Метрическое пространство является совокупностью множества М с за
данным в нем расстоянием з(та, ть) между двумя любыми элементами т „ ,
ть € М, удовлетворяющим следующим условиям:
1.31. Доказать, что в любом коммутативном кольце
n
_
m -fг» / т \п
__
„ « in / т\п
а а = a , (ab) = а о , (a ) = a
mn
а П b U с П (a U b) = (a П b U с) П (a U b).
а П (b U c) U b П с = (с U a Л Ь) Л (a U Ь).

§ 1.11. Задачи и упражнения
89
a(m0, ть) > 0, если та ф тпь, и з(та, ть) = О, если элементы совпадают;
<3(t/1д^ tTlf,) ~ S(ilifc, ^aji
5(m 0, ть ) + 5(ть, m c) < a(ma, mc) (условие треугольника).
Задать метрику в гиперкубе и установить, что она собой представляет.
1.40. Доказать, что в совершенной НФК множества М при замене каждой
операции объединения иа симметрическую разность равенство ие нарушается.
1.41. Установить, является ли форма
M(M i, Мг, Мз) = Mi Л М2 л Ж U Mi Л Mi Л Ms UШ
совершенной.
1.42. Установить, является ли форма
M (M i, М2, Мз) — Mi Л М
2
U Mi U Мз U Мг Л Мз U Mi Л Мз
сокращенной.
1.43. Минимизировать в классе нормальных форм Каитора множество М,
заданное как объединение своих конституент:
М(МЬ М>, Мз, М4) = и(0, 2, 7, 8, 11, 14, 15),
где десятичные числа являются числовыми эквивалентами двоичных векторов,
определяющих соответствующие конституенты этого множества.
1.44. Определить сложность минимальной скобочной формы множества М,
заданного своей нормальной формой:
М = Mi Л Мг Л Мз U Mi Л М2 Л Ms U Mi Л Мз Л М4 Л
Л М6 U М2 Л М4 Л М5 Л Мв.
1.45. Найти число тупиковых НФК множества
M(M i, Мг, Мз, М4) = Mi Л Мг Л Мз U Mi Л Мг Л М4 U Мг Л Мз Л
л м Г л Ж и М 1 л Ж л м 4.
1.46. Определить ранг (число конституент) множества
M(Mi, Мг, ..., Me) — (М4 Л Ms U Mi Л Мг) Л (Mi Л Мз U Ms Л Me).
1.47. Найти минимальную НФК множества М, определенного в четырех
мерном пространстве:
М = U(1 - 00, -110, 0101, - 0 - 1 , 0010, - 0 1 -, 0 - 0-).
1.48. Определить уменьшение мощности сигнатуры мографа GM(M), опре
деляющего множество
М(МЬ М2, Мз, М4) = U(0, 4, 6, 7, 8, 9, 11, 13, 15),
после минимизации в классе НФК.
1.49. Определить мощность класса множеств, каждое нз которых ие содер-
П П
__
жит два пересечения Г1 Mi и П М; в n-мериом пространстве.
tsl 1=1
1.50. Определить уменьшение мощности носителя мографа GM(M), опре
деляющего множество
M (M i, М2, Мз, М4) s U(0, 1, 2, 3, 5, 11, 15),
после минимизации в классе НФК.
1.51. Найти минимальную скобочную форму представления множества
M(M i, Мг, Мз, М4), включающего интервалы 0—01, 01—1, 110—, 01—0 и ие
содержащего интервалы 10—1, 111— и 00-0.
1.52. Записать числа 704, 21, —77 в системах счисления с основаниями
з = 3, 7, 11. Множество цифр симметрическое.

90
Гл. 1. Основы многосортных множеств
1.53. Записать числа 0.6; —56.1 в системах счисления с основаниями з =
= 5, 7. Множество цифр симметрическое, число разрядов после запятой брать
для обеих систем равным 3.
1.54. Записать числа 39.88 и —101 в системах счисления с основанием з =
= 4, 8, 12. Множество цифр асимметрическое в положительную сторону.
1.55. Записать числа 88, 41 в системе счисления с основанием 6 и цифрами
— 1, 0, 1, 2, 3, 4. Число разрядов после запятой взять равным 4.
1.55. Записать число —0.77 в системе счисления с основанием 10 и цифрами
—3, —2, —1, 0, 1, 2, 3, 4, 5, 6. Число разрядов после запятой взять равным 4.
1.57. В системе счисления с основанием 5 записано число 22001. Найти его
десятичный эквивалент. Какому числу будет соответствовать этот же код, если
система счисления десятичная?
1.58. Установить, в какой системе счисления произведено следующее дей
ствие: (23 — 5) + (1 — 642) = 42423. Цифры, стоящие иа месте прочерков, ие
известны.
1.59. Записать числа 71, —16 и 203 в системе счисления с основанием 2-1 .
Чему равен десятичный эквивалент полученного кода, если рассматривать его
как запись в двоичной системе? Множество цифр естественное.
1.60. Доказать следующую теорему: в системе счисления с натуральным
основанием естественное множество цифр позволяет однозначно закодировать
любой количественный эквивалент.
1.61. Обосновать правила перевода целых и дробных чисел из системы с
натуральным основанием R в систему с натуральным основанием Q.
1.62. Установить правила перевода чисел из десятичной системы счисления
в систему счисления с основанием 2 и естественным множеством цифр.
1.63. Установить правила перевода записей из системы счисления с основа
нием —3 и естественным алфавитом цифр в систему счисления с основанием 3
и той же совокупностью цифр.
1.64. Определить, как меняется запись числа при переходе от системы с 5 =
= 3 и симметрическим множеством цифр к системе 5 = — 3 и тем же множеством
цифр.
1.65. Установить правила перевода из системы счисления с основанием 2 с
цифрами 0, 1 в систему счисления с основанием 4 и асимметрическим множе
ством цифр, смещенным в отрицательную сторону.
1.66. Записать в системе счисления с основанием 0.25 число 61. Устано
вить связь между записью чисел в этой системе н записью чисел в четверичной
системе с цифрами 0, 1, 2, 3.
1.67. Найти множество цифр для системы счисления с основанием 0.125,
обеспечивающее однозначное представление любого числа.
1.68. Записать в дополнительном коде в системе счисления с основанием 5
и естественным множеством цифр числа 60, —15 и —607.
1.69. Записать в дополнительном коде число 0 в системе счисления с осно
ванием 6 и естественным множеством цифр.
1.70. Записать в обратном коде в системе счисления с основанием 7 и есте
ственным множеством цифр числа 55, —70 и 118.
1.71. Записать число 0 в обратном коде в системе счисления с 5 = 11 и
естественным множеством цифр.
1.72. Записать в дополнительном коде число —65 в системе счисления с 5 =
= 4 и цифрами —3, —2, —1, 0.
