Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§2.4. Полнота. Построение суперпозиций булевых функций 111

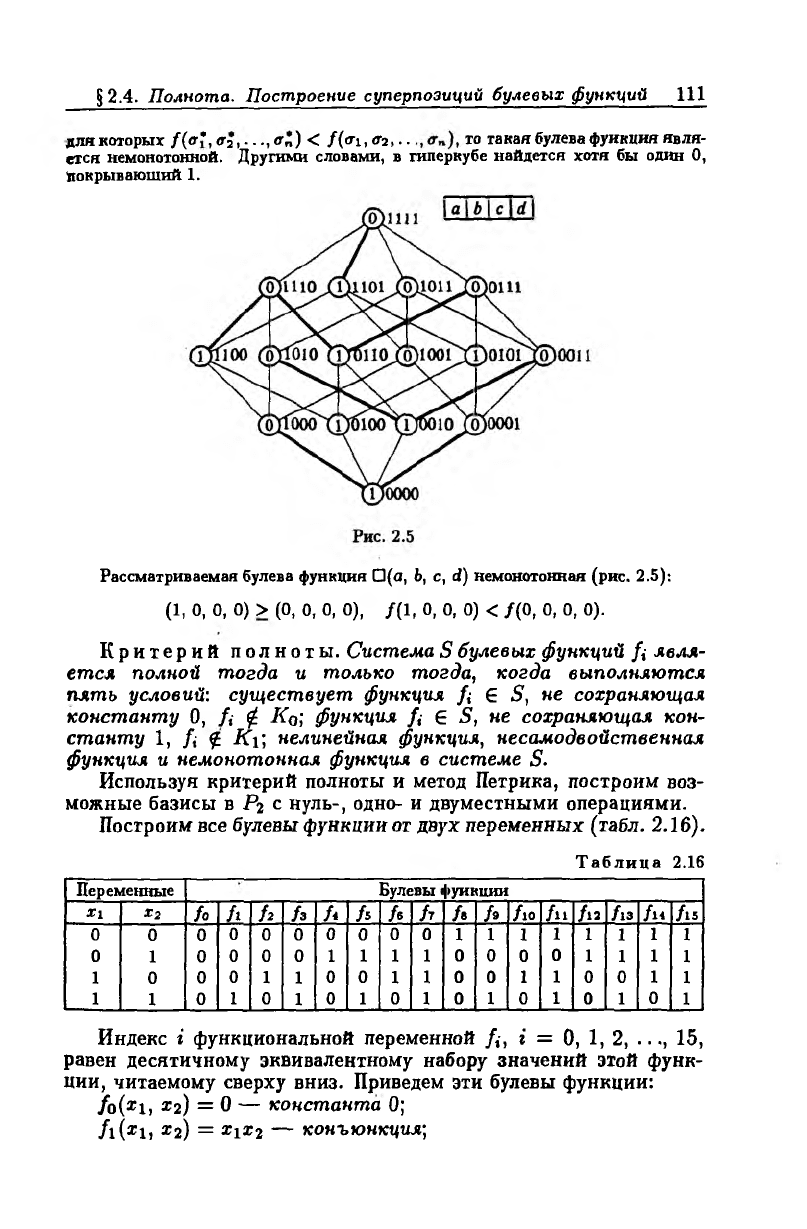
для которых / ( 0'*,0'2,-..,0'n) < /(<П> «Ь, • ■ 10 такая булева функция явля

ется немонотонной. Другими словами, в гиперкубе найдется хотя бы один О,

Покрывающий 1.

Рассматриваемая булева функция □(а, Ь, с, d) немонотонная (рис. 2.5):

(1, 0, 0, 0) > (0, 0, 0, 0), /(1, 0, 0, 0) < /(О, 0, 0, 0).

Критерий полноты. Система S булевых функций fi явля

ется полной тогда и только тогда, когда выполняются

пять условий: существует функция fi 6 S, не сохраняющая

константу 0, /,• ^ Ко', функция fi 6 S, не сохраняющая кон

станту 1, f £ К \’, нелинейная функция, несамодвойственная

функция и немонотонная функция в системе S.

Используя критерий полноты и метод Петрика, построим воз

можные базисы в Р2 с нуль-, одно- и двуместными операциями.

Построим все булевы функции от двух переменных (табл. 2.16).

Таблица 2.16

Переменные Булевы

>уикции

х2

/о

/а

/з и

}ь

/ 7

/ * / 9

/м

/и

Л з

/14 /is

0 0

1 1

1 0

0 0 0 1 1 1 1

0 0

1 0

0 0

1 1

0 0 1 1 0 0 1

1 0

0 1 0

0 1

Индекс i функциональной переменной /,-, i = 0, 1, 2, ..., 15,

равен десятичному эквивалентному набору значений этой функ

ции, читаемому сверху вниз. Приведем эти булевы функции:

fo(xi, хг) = 0 — константа 0;

Л (х1, х2) = xix2 — конъюнкция;

112

Гл. 2. Математическая логика

/ 2(2 1 , х2) - = ® i*2 = x i V х2 = xi ->■ Х2 = xi х2 — левая

коимпликация (ч и х ае т ся “н е е сл и ц , т о х 2” ; п р е ф и к с к о — ох

л а х . c o n v e rs u s — о б р а т н ы й );

/ з ( * 1 , * 2) = Z lX 2 V X XX 2 = Х\]

f i ( x i, х2) = х\х2 = х\ V 4 - ®2 = **- х2 — правая

коимпликация;

/ 5 О 1 , * 2) = Х1Х2 V ххх2 = аг2;

/ в ( * 1 , х2) = x i x 2 V Х1Х2 = х\ ф х2 — сложение по модулю 2

и л и неравнозначности, неэквивалентности;

/ 7 (2:1 , агг) = V ®2 — дизъюнкция;

/ в ( * 1 , х 2) = x i *2 = x i V ar2 = x t о х2 — функция Вебба;

}э (х \, х2) = X i x 2 V x i г г = x i ~ х2 — ф у н к ц и я эквивалент

ности, равнозначности;

/io (* i > * 2) = Х2 — отрицание;

/ n ( x i , х 2 ) = x i x 2 V zx X 2 V x i 2;2 = х 2 V x i = x i * - х2 — правая

импликация (ч и т а е т с я “е с л и х2 , т о x j ” );

/ i 2( x i , * 2) = x i — отрицание;

/ i 3 ( x i , Х2) — ххх2 V X iX 2 V x i x 2 = X i V X2 = x i —> x 2 — левая

импликация (ч и т а е т с я “е с л и х\, то * 2” );

/ 14(2:1 , х 2) = х {х2 V x i x 2 V Х\Х2 = х\ Ух2 = х\\х2 — функция

Шеффера;

h s { x u * 2) = 1 — константа 1 .

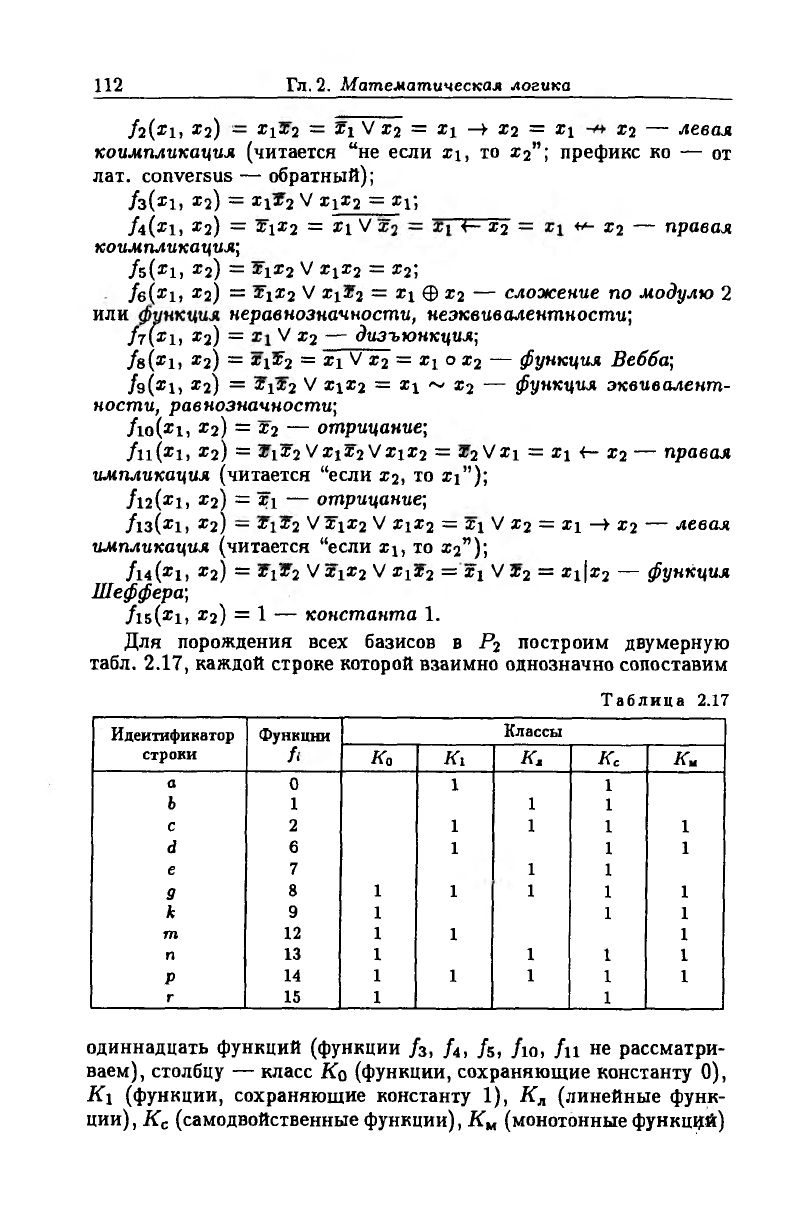
Д л я п о р о ж д е н и я в с е х б ази со в в Р2 п о с тр о и м д в у м е р н ую

т а б л . 2 .1 7 , к а ж д о й с т р о к е к о то ро й в з а и м н о о д н о зн а ч н о с о п о ст а в и м

Таблица 2.17

Идентификатор

Функции

Классы

строки

Ко

кж

Кс

Кы

1 1

с 2

1 1

е 7 1

8 1

1 1

т 12

1 1

п 13

1 1

14 1

1 1

о д и н н а д ц а т ь ф у н к ц и й (ф у н к ц и и / 3 , / 4 , / 5 , / ю , / п н е р а с с м а т р и 

в а е м ), с т о л б ц у — к л а с с Ко (ф у н к ц и и , с о х р а н я ю щ и е к о н с т а н т у 0),

К \ (ф у н к ц и и , с о х р а н я ю щ и е к о н с т а н т у 1 ), К л (л и н е й н ы е ф у н к 

ц и и ), К с (с ам о д в о й с т в е н н ы е ф у н к ц и и ), К м (м о н о то н н ы е ф у н к ц и й )

§2.4. Полнота. Построение суперпозиций булевых функций 113

и в клетке (г, j) ставим 1, если i-я функция не принадлежит j-uy

классу, в противном случае клетку (i, j) оставляем пустой.

Методом Петрика преобразуя мультипликативно-аддитивную

форму в аддитивно-мультипликативную, порождаем все покрытия

столбцов строками этой таблицы:

(<7V&VmVnVpVr)(aVcVdV(7VmVp)(bVcVeV<7VnVp)&

&(aV6VcVdVeV^VA:VnVpV r)(cV d V }V & V mV nV p) =

= (g\/ akV kc\/ kd\/ mV anV cnV dn\/ p\/ ar\/ crV rd) fc

& (6 V с V e V g V n V p)(cV d V 5 V к V m V n V p) =

= (g\/ akV kc\/ kdV m V an V cn\/ dnV pV ar\/ crV rd) &

&(cV<7VnVpVbdVb&V bm V ed V ek V em) =

= g V p V abfc V ксУ ап\/ cn\/ dn\/ ake V fcbd V ked V

V me V mn V Ь т V me V cr V rbd V red =

= 5 V p V fcc V an V cn V dn V тс V mn V Ь т V me V

У cr У abk V afce V fcbd V ked V rbd V red.

Каждое из полученных покрытий яг,- порождает базис Д :

я-i = {</} н- Вг = {0} — базис Вебба;

■к2 = {р} <->• В2 = {|} — базис Шеффера;

тг3 = {Л, с} <-)• В 3 = {-*, ~};

7Г4 = {a, n} В 4 = {—>, 0} — импликативный базис;

7г5 = {с, п} <-)■ В5 = {->, -»};

яте = {d, п) ++ Вв = {—>, 0 };

7Г7 = { т, с} В7 = {-», } — коимпликатиеный базис-,

7Tg = { т, n} = {—>, } — импликативный базис-,

7гд = {Ь, т } f* Вд = {&, } — конъюнктивный базис Булл-,

jtjo = { т , e}<-)-Bio = {&> } — дизъюнктивный базис Буля-,

тгц = {с, г } н - Вц = {-^>, 1 } — коимпликатиеный базис;

ТГ12 = {а, Ь, к} н- В12 = {~, 0};

7Г13 = {а, к, е} <->• В13 = {~, V, 0};

7Ti4 = {Л, Ь, d} f-> В г4 = {0 , &, ~ };

тг15 = {fc, е, d} н- В15 = {0 , V, ~};

я’хв = { г, Ь, d} н- В16 = {0 , &, 1} — базис Жегалкина;

*17 = {»*, е, d} н- В 17 = {0 , V, 1}.

Получено 17 базисов, в каждом из которых нельзя вычеркнуть

ни одну функцию без потери полноты в Р2. Каждому сложному

высказыванию в системе {V, &, } соответствует эквивалентное

высказывание в любом из этих базисов. Например, высказыванию

114

Гл. 2. Математическая логика

“не о или Ь и с” в импликативном базисе {— } соответствует

эквивалентное высказывание “если а, то не если Ь, то не с”:

а V Ьс = а —У bc = а —ybV с = а —* (Ь —у с) .

Техническая реализация базисных функций может быть осно

вана на использовании различных физических явлений, напри

мер, импликация и коимпликация может быть основана на ис

пользовании магнитных явлений, а функции Шеффера и Веб-

ба — на использовании явлений в полупроводниках.

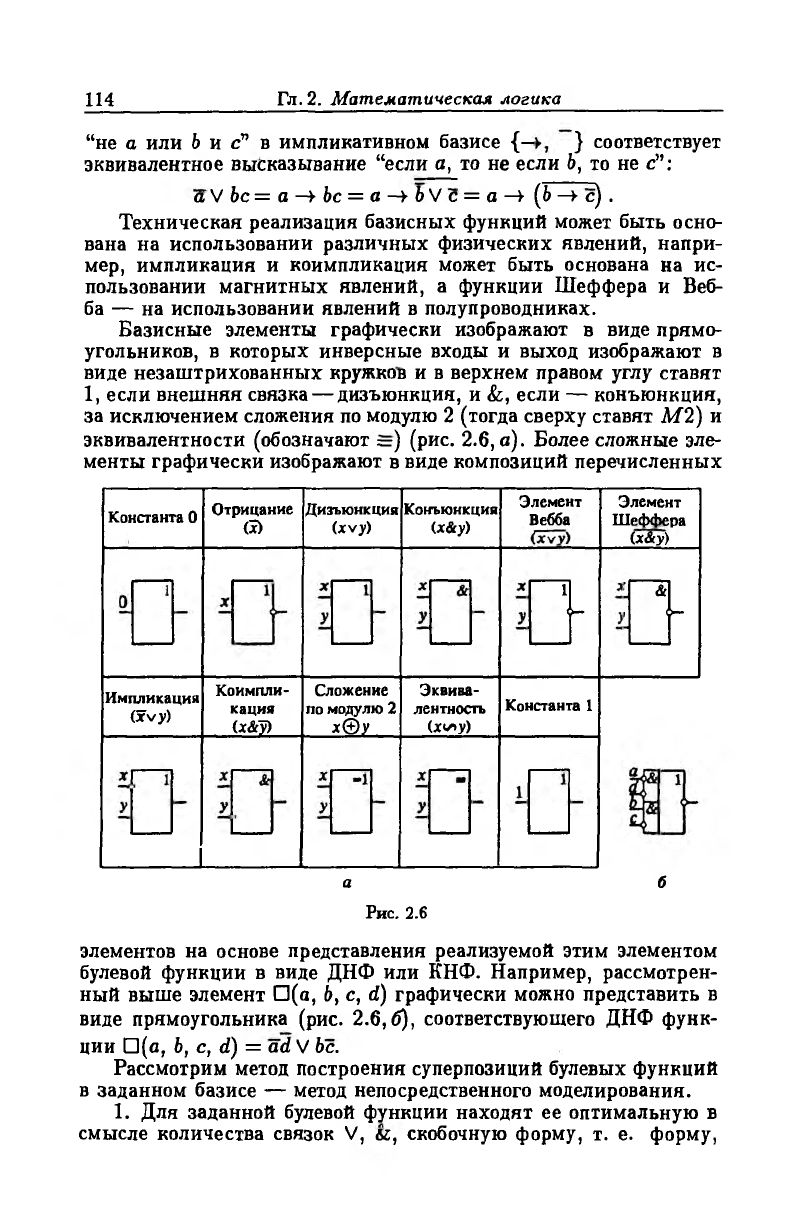
Базисные элементы графически изображают в виде прямо

угольников, в которых инверсные входы и выход изображают в

виде незаштрихованных кружков и в верхнем правом углу ставят

1, если внешняя связка — дизъюнкция, и &, если — конъюнкция,

за исключением сложения по модулю 2 (тогда сверху ставят М2) и

эквивалентности (обозначают =) (рис. 2.6, а). Более сложные эле

менты графически изображают в виде композиций перечисленных

Константа О

Отрицание

(5)

Дизъюнкция

(xvy)

Конъюнкция

(х&у)

Элемент

Вебба

Элемент

Шеффера

(х&у)

[ 1 О

Импликация

(jfvy)

Коимпли

кация

_ М 2 _

Сложение

по модулю 2

х®У

Эквива

лентность

(х</<у)

Константа 1

а б

Рис. 2.6

элементов на основе представления реализуемой этим элементом

булевой функции в виде ДНФ или КНФ. Например, рассмотрен

ный выше элемент П(а, 6, с, d) графически можно представить в

виде прямоугольника (рис. 2.6,6), соответствующего ДНФ функ

ции П(а, Ь, с, d) = ad V be.

Рассмотрим метод построения суперпозиций булевых функций

в заданном базисе — метод непосредственного моделирования.

1. Для заданной булевой функции находят ее оптимальную в

смысле количества связок V, к , скобочную форму, т. е. форму,

§ 2.4. Полнота. Построение суперпозиций булевых функций 115

представляющую собой композицию первичных термов х°‘,

* = 1, 2, ..., п, операций V, &, и скобок, вводимых в выражение

булевой функции на основе использования закона дистрибутивно

сти. _

2. Выражают классические связки V, &, в виде суперпози

ции заданного базиса.

3. Подставляют результаты п. 2 в выражение, полученное в

п. 1^ отмечая штриховой линией стыки блоков, моделирующих V,

&, в заданном базисе.

4. Анализируя стыки, устраняют избыточность логической схе

мы, используя закон двойного отрицания.

Пример 2.6. Синтезировать логическую схему, реализующую булеву функ-

ЦШ° , , , т \ _ f 1 на - 0 - 10, 10 - 11, 0 - 101,

/(ri, х2, хз, xit xs) - иа 1 _ ю - , 1 _ 001, 0 - 1 0 0

в базисе В = {—>, 0}.

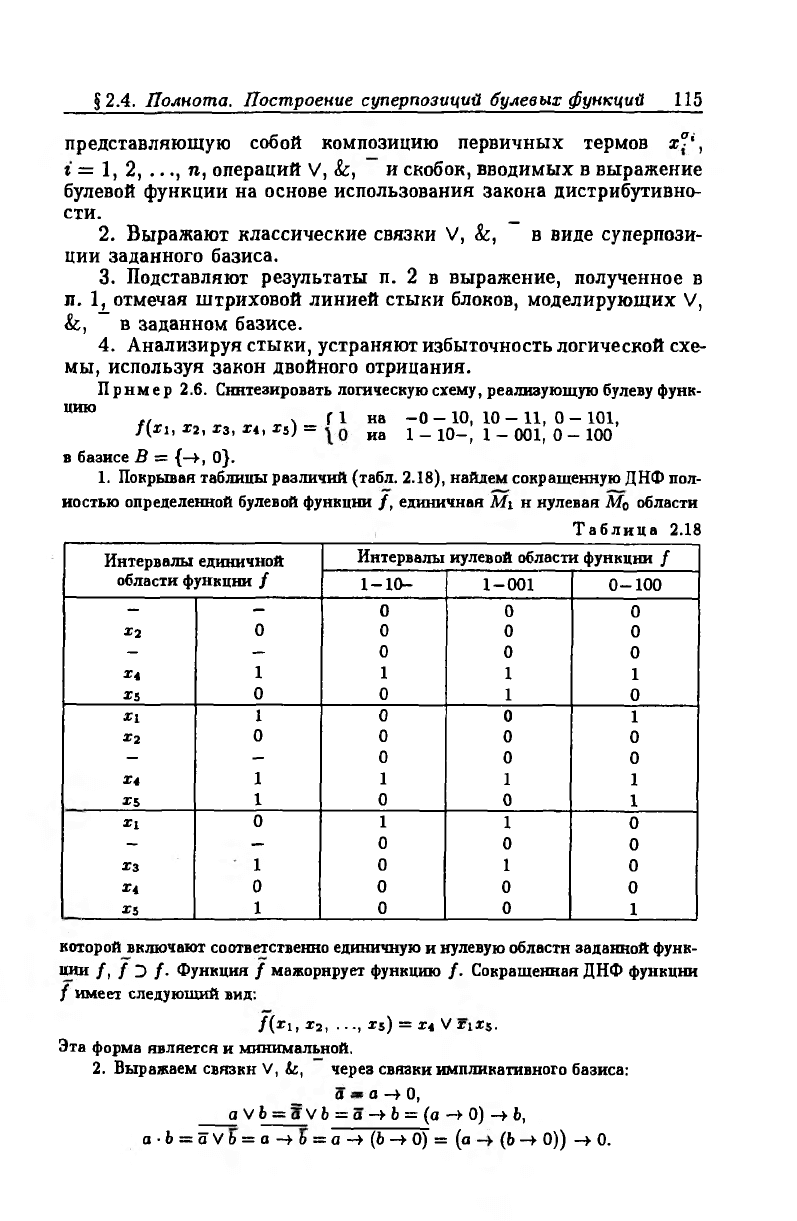
1. Покрывая таблицы различий (табл. 2.18), найдем сокращенную ДНФ пол

ностью определенной булевой функции / , единичная Mi н нулевая Мо области

Таблица 2.18

Интервалы единичной

области функции /

Интервалы нулевой области функции /

1 - 1 0 -

1 - 0 0 1

0 - 1 0 0

- -

- —

Хь

XI 1 0

- -

Xi 1 1

Хь

1 0

0 1

- —

Хз

0 0

Хь

1 0 0

которой включают соответственно единичную и нулевую области заданной функ

ции / , / Э /■ Функция / мажорирует функцию /. Сокращенная ДНФ функции

/ имеет следующий вид:

/(*i, х2, ..., rs) = *4 V * i i s .

Эта форма является и минимальной.

2. Выражаем связки V, fc, через связки импликативного базиса:

_ а — а -> 0,

___

а V Ь = а V Ь = а —► Ь = (о —► 0) -> Ь,

o - i = 5 V b = o -+6 = a-+()i-+ 0) = (а (Ь -> 0)) -> 0.

116

Гл. 2. Математическая логика

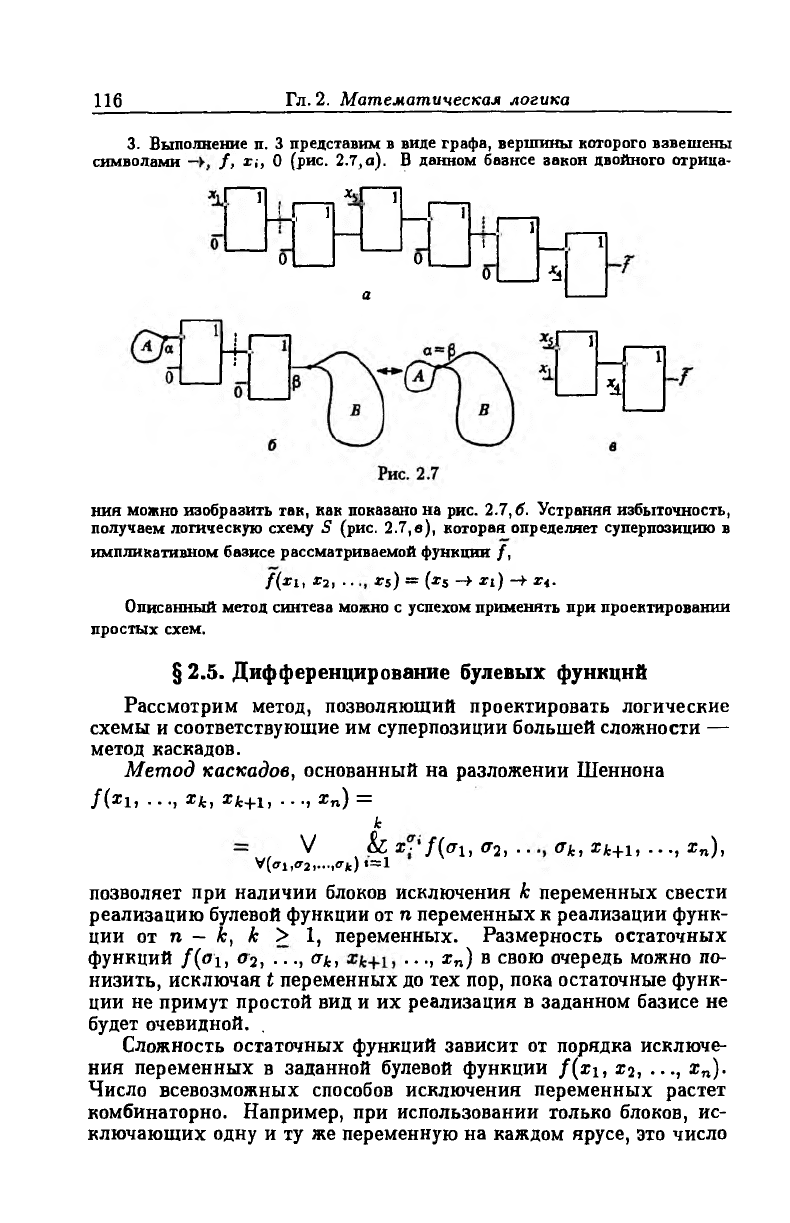
3. Выполнение п. 3 представим в виде графа, вершины которого взвешены

символами — / , х;, О (рис. 2.7,а). В данном базисе закон двойного отрица-

*■>

}

, 1 1

•S

хл

ния можно изобразить так, как показано на рис. 2.7, б. Устраняя избыточность,

получаем логическую схему 5 (рис. 2.7,в), которая определяет суперпозицию в

импликативном базисе рассматриваемой функции /,

/(п , х2, . . xs) = (xs -> ц ) -> г«.

Описанный метод синтеза можно с успехом применять при проектировании

простых схем.

§ 2.5. Дифференцирование булевых функций

Рассмотрим метод, позволяющий проектировать логические

схемы и соответствующие им суперпозиции большей сложности —

метод каскадов.

Метод каскадов, основанный на разложении Шеннона

f(x 1, . . ., Xht Xk+\, . . ., ®n) =

— V & X- f(<T\, 02, . . Ok, Xk+1, • • ., xn),

V(<ri,<r2,...,<rk) »=1

позволяет при наличии блоков исключения к переменных свести

реализацию булевой функции от п переменных к реализации функ

ции от п — к, к > 1, переменных. Размерность остаточных

функций /(<7i, 02, • • -, Ок, • • •) ®п) в свою очередь можно по

низить, исключая t переменных до тех пор, пока остаточные функ

ции не примут простой вид и их реализация в заданном базисе не

будет очевидной. .

Сложность остаточных функций зависит от порядка исключе

ния переменных в заданной булевой функции f(x i, х2, ..., хп).

Число всевозможных способов исключения переменных растет

комбинаторно. Например, при использовании только блоков, ис

ключающих одну и ту же переменную на каждом ярусе, это число

§2.5. Дифференцирование булевых функций

117

равно п!, но на каждом ярусе можно исключить не только одну

и ту же переменную, но и различные переменные; далее, можно

исключать на каждом шаге различное число переменных (одну,

две, три и т. д.). Выбор оптимального исключения переменных

перебором всех способов исключения — трудоемкий процесс.

Оптимальное исключение переменных ищут, используя эври

стические критерии, один из которых основан на использовании

понятия производной от булевой функции.

Производная первого порядка д//дх{ от булевой функции /

по переменной ж,- есть сумма по модулю 2 соответствующих оста

точных функций:

— f (хl, Х2, • • ., %i—l, 1) • • ч Хп) ф

ф f(x 1, Х2, ..., %i—i, 0, ..., хп), (2.13)

где f(xi, Х2, ..., 1, ..., хп) — единичная остаточная функ

ция; f(x 1, х2, ..., *i_i, 0, . . х„) — нулевая остаточная функция;

ф — сумма по модулю 2.

Единичная остаточная функция получается в результате при

равнивания переменной х,- единице, нулевая — приравниванием

Xi нулю.

Пример 2 .7 . Вычислим производную df/dxi от булевой функции

/ (* 1, х2, * 3)|i = V (0 , 4 , 7 ),

где 0, 4, 7 — десятичные эквиваленты двоичных наборов, на которых функция

/ равна 1:

/ ( * 1, Х2, хз) = *2*3 V *1*2 *3.

Согласно определению

0 /

— (*2*3 V Х2Х3) © *2*3 — (*2*3 V * 2 *з )& * 2 *3 V (*2*3 V * 2*3) & *2*3 =

= (*2*3 V *2 *з)(*2 V *3) V (*J V *з)(*2 V * з) & * 2*3 = *2*3.

Производная первого порядка df/dx; от булевой функции /(*i, *2, ..., *п) опре

деляет условия, при которых эта функция изменяет значение при переключении

переменной ц (при изменении значения *; на противоположное).

В рассмотренном примере функция /( * 1, *2, *3) изменяет свое значение а

на (F(<г —> IF), or = 0, 1, при изменении значения переменной * i, <74 —> Fi

при условии, что конъюнкция *2*3 принимает значение “истинно”, т. е. * 2 =

=**з = 1.

Смешанной производной dkf/(dxildxi2...dxik) от булевой

функции / по переменным Xi2, ..., Xik называется выраже

ние вида

__________________

_________________________= J L (

_____________

^ 1 1

___________

' I , 2 н)

dxit dxi2... d x i^ dxik dxXk \ dxi2... d x ^ J

118

Гл. 2. Математическая логика

Смешанную производную fc-ro порядка дк//(дх{1 дх{2.. .дх,t)

вычисляют, применяя соотношение (2.13) к раз фиксацией пере

менных xtl, х»2, . . Х{к (порядок фиксации переменных не имеет

значения); количество упорядочиваний равно к\

Производная к-го порядка dkf/d(xii, х,-2, ..., Х{к) от булевой

функции f(x 1, х2, ..., хп) по переменным х^, х,-2, ..., ц к опре

деляет условия, при которых эта функция изменяет значение при

одновременном изменении значений переменных х ^ , х,-2, ..., x1Jt.

Согласно Бохману производная к-го порядка dkf/d(xil,

х,-2, ..., Xik) от булевой функции f(x i, х2, ..., хп) по перемен

ным xtl, х,-2, ..., х{к равна сумме по модулю 2 всех производных

первого порядка, вторых, третьих и т. д., k-х смешанных про

изводных при фиксации переменных х,п х,-2, ..., x,t :

» Ч - s r £ L r - v - a' f

........, в», ,.f

a3/

dr,- dx^ d r, ® • • • ® qx^ gXii', _ 0 ^

® 2 Я ,. Я * • • •Ф Яг, Я*.- . я*.. ’ ^2Л5^

м.*

i, j, s, ... — гх, i2, ..., t'jfc.

Пример 2.8. Определим условия переключения выходного канала / логи

ческой схемы, реализующей булеву функцию /(*i, 12 , хз) = xix2 V Х1Х3, прн

переключении каждого входного канала, первого и второго каналов одновременно

и всех трех каналов x i, хз, хз одновременно. Имеем

д f df

ft f

= n i j ® Xl = X l( x 2 ® 1) = x ix 2.

Условие df /дх 1 = 1 является условием переключения выходного канала

/ при переключении входного канала п : при подаче на второй канал 1 или на

третий 0, при переключении первого канала х\ с с на 7 (<г -> 7) выходной канал

переключается с с на 7 (<г —у 7, с — 0, 1). Выходной канал / переключается

(<г —у 7) при переключении входного канала ц (<? -* 7), если xi = хз = 1, и /

переключается (<г —> а), когда переключается хз (7 —> <г) при xi = 1, Х2 = О,

и = 0, 1. Далее находим

д2/ - i -■> i —

— 1 — 1 ® 13 = х3,

dxi 8x2

а2/ а/ df а2/

дх2 \ЭХ1)

= (л?2 V хз) ® Г1Г3 ® Хз

d (x i, Х2) d x i д х 2 d x id x j

= (Х2 \/ЛГз)фХз(Х1 ® 1) = (Х2\/Хз)®Х1Хз — (х 2 VX3) & Х1Х3 V(x2 V X 3)& X lX 3 =

= (хг V Хз)(Х1 V Хз) V Х2Х3 & Х 1Х 3 = Хз V X lХ2 V Х1Х2Х3 = Хз V Х1Х2 V XIХ2-

§ 2.5. Дифференцирование булевых функций

__________

119

Выходной канал / переключается при любом одновременном переключении

входных каналов x i, х2, когда хз = 0, или независимо от состояния входного

канала хз при переключении xi и х2 с 11 на 00 или с 00 на 11. Вычислим

d?f/d(xi, х2, хз):

э (df\ _ _ а2/ д (df\

( э г J “ ® 2’ дхг дхз дх3 { дх2 ) *1'dxi дхз дхз

а3/

\dx2dx3)

dxi дх2 дхз д ц

а3/ а/ а/ а/ а2/ а3/ а2/

d(xi, Х2, хз) д ц дх2 дхз дх\ дхг д ц дхз дхъдхз

йЗ /

ф -5

----

-----------

д ц дх2 дхз

= (хз V X1X2 V X1X2) & X 1X 2 V (хз V X1X2 V X1X2) & X 1X 2 =

= (хз V X1X2 V Х1Хг)(Х1 V X2) v хз(х 1 V X*2 )(x 1 V X2)X1X2 =

= X1X3 V X1X2 V X2X3 V X1X2 V X1X2X3 =

= X1X2X3 V X1X2X3 V X1X2X3 V X1X2X3 V X1X2X3 V X1X2X3.

При переключении входного вектора 4 н З,6 н 1и 7« 0 выходной канал

/ переключается.

Критерий оптимального исключения переменных в методе кас

кадов заключается в исключении сначала переменных, при пере

ключении которых булева функция переключается при максималь

ном числе условий. Это максимальное число определяется весом

производной.

Весом производной от булевой функции называется число кон

ституент этой производной.

При использовании блоков, исключающих к переменных, на

ходят производные к-го порядка от реализуемой функции и ищут

максимальное значение веса производной P(dkf/d(xiltxi3,...

я,-*)), которое и определяет исключаемые переменные. Для

полученных остаточных булевых функций снова находятся про

изводные: определяются веса, а производная от рассматривае

мой остаточной функции, имеющая максимальный вес, опреде

ляет соответствующие переменные, которые исключаются на этом

120

Гл. 2. Математическая логика

ярусе для этой остаточной функции, и т. д., пока остаточные функ

ции не будут иметь простую реализацию.

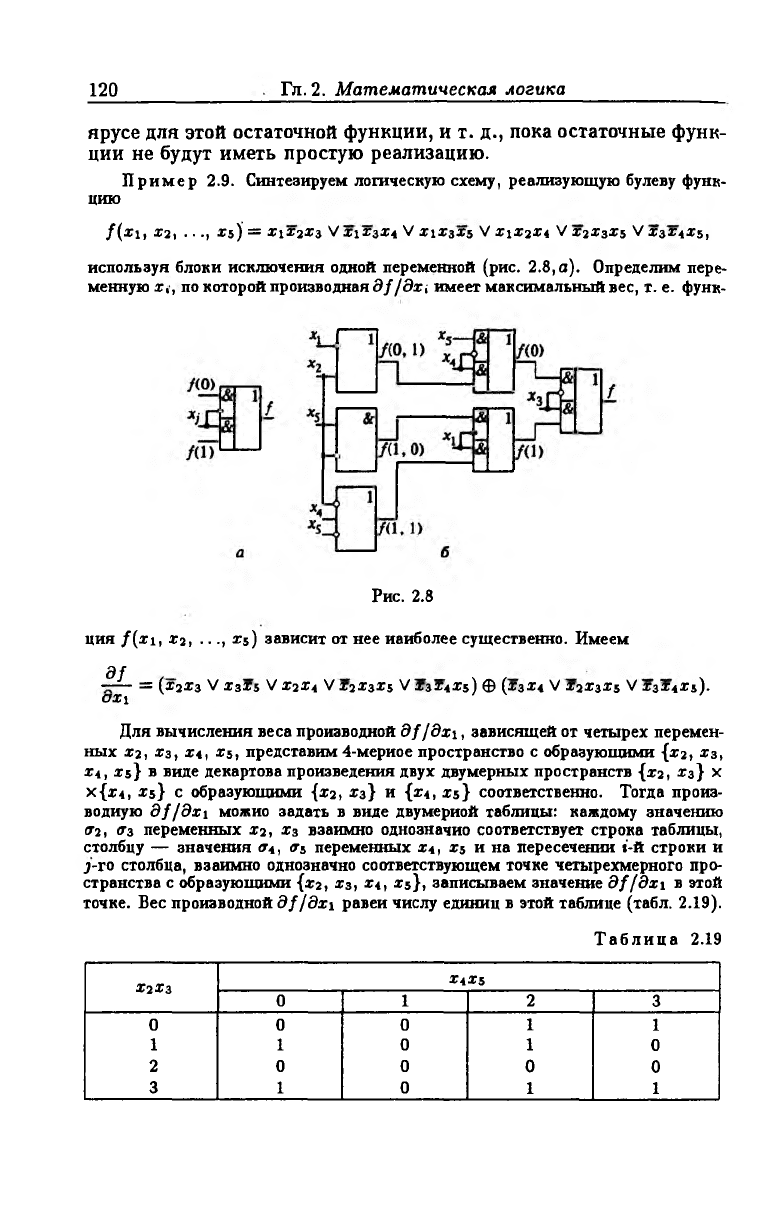
Пример 2.9. Синтезируем логическую схему, реализующую булеву функ

цию

/(* 1, *2, . . ., Xs) = *1*2 *3 V *1*3 *4 V *1*3X 5 V *1*2 *4 V *2*3*5 V *3*4*5,

используя блоки исключения одной переменной (рис. 2.8, а). Определим пере

менную*!, по которой производная df /da имеет максимальный вес, т. е. функ-

Рис. 2.8

ция /( * 1, * 2, ■ ■., *5) зависит от нее наиболее существенно. Имеем

—

----

= (*2*3 V *3*5 V *2*4 V * 2* 3*5 V * 3 *4 * 5 ) ф (*3*4 V *2*3*5 V *3*4 * 5 ).

ОХ 1

Для вычисления веса производной df /дх i , зависящей от четырех перемен

ных *2, *з, * 4, xs, представим 4-мериое пространство с образующими {*2, *з,

*4 , * 5 } в виде декартова произведения двух двумерных пространств {*2, *3 } х

х {* 4, * 5 } с образующими {*2, *з} и {*4 , *5 } соответственно. Тогда произ

водную df /дх 1 можно задать в виде двумерной таблицы: каждому значению

<Г2, <тз переменных *2, *з взаимно однозначно соответствует строка таблицы,

столбцу — значения <Т4, <т$ переменных *4, *5 и на пересечении »-й строки и

j-ro столбца, взаимно однозначно соответствующем точке четырехмерного про

странства с образующими {*2, *з, *4, *5 }, записываем значение df /дх i в этой

точке. Вес производной df /dx 1 равен числу единиц в этой таблице (табл. 2.19).

Таблица 2.19

* 2*3

* 4*5

0 0 0 1

0 1

2 0 0

1 1