Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§2.5. Дифференцирование булевых функций

121

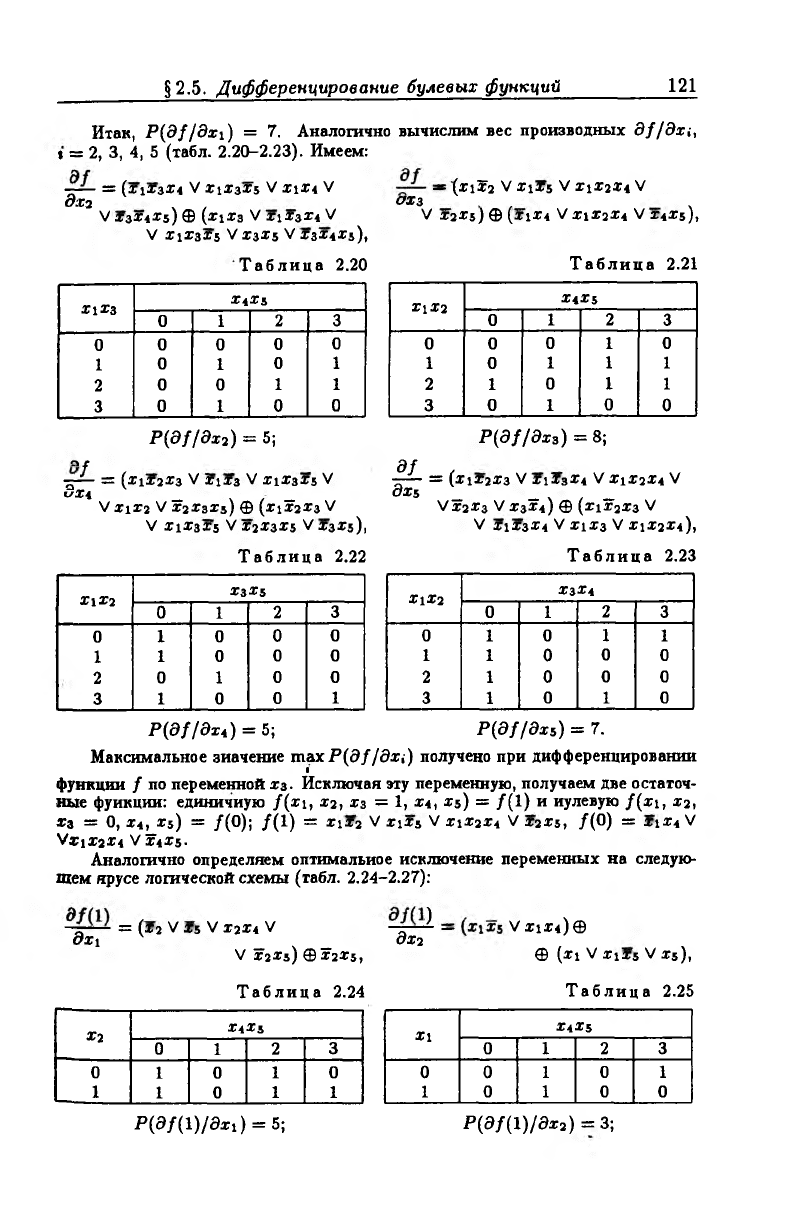
Итак, P(df/dxi) = 7. Аналогично вычислим вес производных df/dn,

» = 2, 3, 4, 5 (табл. 2.20-2.23). Имеем:

- - = (*1X3X4 V *1X3X5 V Х1Х4 V — (xi?2 V Х1Х5 V Х1Х2Х4 V

&ГЗ OXz х

VX 3X4^s) 0 (Х1Л3 V X1X3I4 V V X2tf5) 0 (Х1Х4 V X1X2X4 V 14^5),

V X1X3X5 V X3X5 V X3X4X5),

Т абл ица 2.20 Т аблица 2.21

XlXi

Х4Х5

0 1

2 3

0 0

0 1

0 0 1 1

0 1

Х1Х2

Х4Х5

0 1

0 0

1 0 1

0 1

P(df/dx2) = 5;

а/

•5 -^ - = (Х1Х2Х3 V Х 1Хз V Х1Х3Х5 V

"Х4 — ч / _

V x ix 2 V Х2Х3Х5) ® (Х1Х2Х3 V

V Х1Х3Х5 V Х2Х3Х5 V Х3Х5),

Т абли ца 2.22

P{df/dx 3) = 8;

3/ ,

- — = (Х1Х2Х3 V Х1Х3Х4 V Х1Х2Х4 V

9X5 _ _ _

VХ2Х3 V Х3Х4)®(Х1Х2ХЗ V

V Х1Х3Х4 V Х1Х3 V Х1Х2Х4),

Т аблица 2.23

Х1Х2

Х3Х5

1 0

0 0

0 1

0 0

3 1

0 1

Х1Х2

Х3Х4

0 1

1 1 0

2 1 0

0 0

3 1

Р(Э //в* 4) = 5; Р(Э//Эх 5) = 7.

Максимальное значение т а xP(df /дц) получено при дифференцировании

функции / по переметюй хз. Исключая эту переменную, получаем две остаточ

ные функции: единичную /(х 1, Х2, хз = 1, Х4, Х5) = / ( 1) и нулевую /(х 1, Х2,

*3 = 0, х 41_х5) = /(0); / (1) = x ix 2 V Х1Х5 V Х1Х2Х4 V Х2Х5, /(0) = Х1Х4 V

V*lX2X4 V Х4Х5.

Аналогично определяем оптимальное исключение переменных на следую

щем ярусе логической схемы (табл. 2.24-2.27):

= (Х2 V Х5 V Г2Х4 V ~яГ~^ — V * 1*«) ®

8*1 _ ч _ дх2

V Х2Х5) ® Х2Х5, ® (xi V Х1Х5 V xs),

Т абл ица 2.24 Т аблица 2.25

Х2

Х4Х5

0 1

0 1 1

Х4Х5

0 1 2 3

0 0 1

0 1

0 1 0 0

Р (а /( l)/ax i) = 5;

P(a/(i)/ax2) = 3;

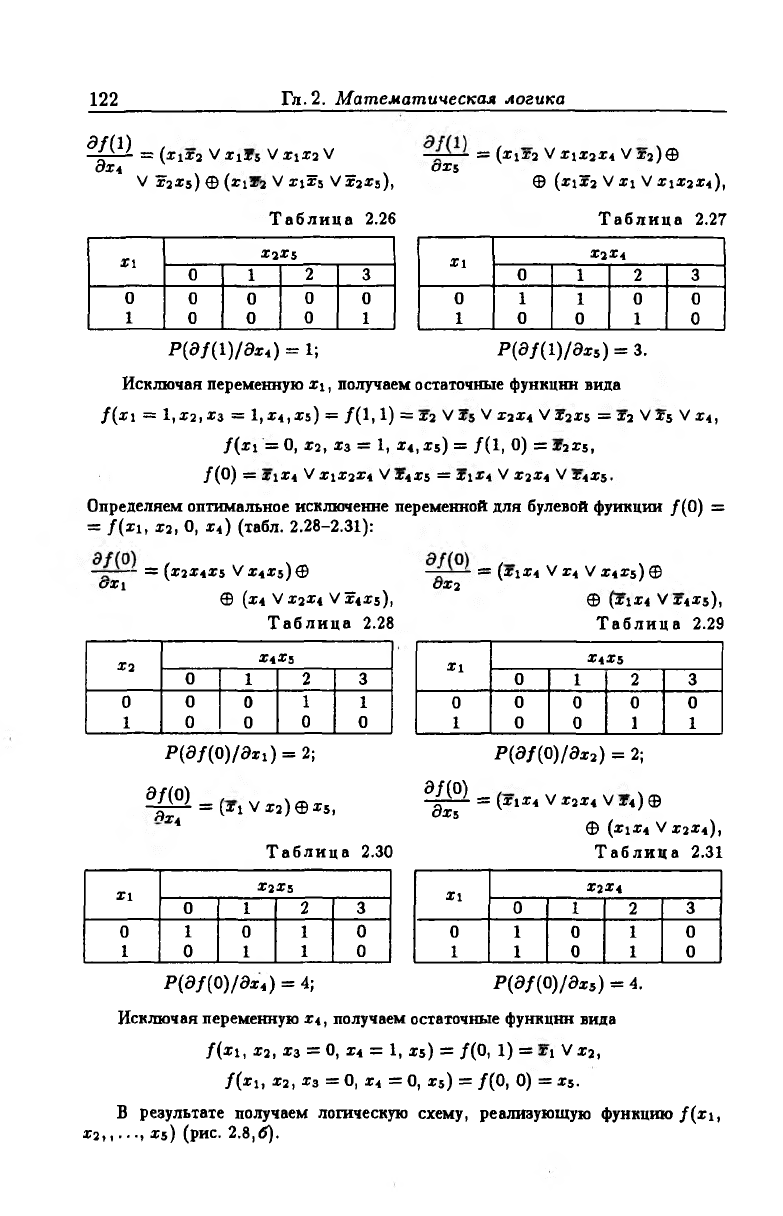
122

Гл. 2. Математическая логика

т = (xix 2 V XlXS V Ц Х 2 V = (xix 2 V ц х щ V х 2) ®

9x4 _ _ _ ах5 _

V Х2Х5) ® (x ix 2 V xjxs V Х2Х5), © (xtx2 V xi V Х1Х2Х4),

Таблица 2.26 Т аблица 2.27

Х2Х5

1 0 0

Х2Х4

1 2 3

0 1

0 0

1 0

P(8f( 1)/ах4) = 1; Р(а/(1)/вх*) = з.

Исключая переменную x i, получаем остаточные функции вида

/(х 1 = 1,Х2,Хз = 1,Х4,Х5) = /(1, 1) = Х2 Vx5 v Х2Х4 V Х2Х5 = l j V ljV Х4,

/(х 1 = 0, х2) Хз = 1, х4, х5) = / ( 1, 0) = хиь,

/(0) = Х1Х4 V Х1Х2Х4 V Х4Х5 = Х1Х4 V Х2Х4 V Х4Х5.

Определяем оптимальное исключение переменной для булевой функции /(0) =

= /(х 1, х2, О, Х4) (табл. 2.28-2.31):

= (Х2Х4Х5 V Х4Х5) Ф = (X1X4 V Х4 V Х4Х5) ф

C/Xi _ ад?2

Таблица 2.28 Т аблица 2.29

х2

Х4Х5

2 3

Х4Х5

2 3

0 0 0

0 1

P(a/(0)/a*i) = 2; P(df(0)/dx2) = 2;

^ = ( X 1VX2)©X5, ^ = (X1X4 VX2X4 VX4)©

14 ф (Х1Х4 VX2X4),

Таблица 2.30 Т абл ица 2.31

Х2Х5

2 3

0 1 0

1 0

Х2Х4

0 1

1 0 1

1 1

Р(д/{0)/дц) = 4; Р(3/(О)/0хв) = 4.

Исключая переменную Х4, получаем остаточные функции вида

/ ( X 1, Х2, Хз = О, Х4 = 1, Х5) = /(0, 1) = XI V х2,

/(х 1, х2, Хз = О, Х4 = О, х5) = /(0, 0) = х5.

В результате получаем логическую схему, реализующую функцию /(х 1,

Х2,,..-, х5) (рис. 2.8,(5).

§2.6. Разложение функции в заданной точке пространства 123

Критерий оптимального исключения переменных имеет эври

стический характер, что основано на предположении о том, что

чем больше вес производной P(df/dxi), тем больше функция /

зависит от переменной Если имеются блоки исключения к пе

ременных, то построение схемы проводят аналогично, вычисляя

вес производных А;-го порядка Р(дк f /д(х^, х,-2, ..., х,*)).

§ 2.6. Разложение булевой функции

в заданной точке пространства

В дискретной математике отсутствует понятие предела, однако

в выражениях (2.13)-(2.15) используется термин “производная”.

Это связано с разложением булевой функции в ряд, аналогичный

ряду Маклорена в точке 00.. .0 или ряду Тейлора в произволь

ной точке пространства. Рассмотрим данные разложения булевой

функции f(xi, х2, ..., хп).

Две функции fa и fp называются взаимно ортогональными,

если их конъюнкция равна 0: fakfp — 0. Выражение (2.11)

эквивалентно равенству п

(y(<Ti,<ra,...,»n))

(/(<>■ 1,0,2,-,0п)=1)

где — сложение по mod 2, так как ск\//3 = а ф /3 ф а /3 и кон

ституенты единицы функции f(xi, х2, ..., хп) попарно взаимно

ортогональны.

Заменим в выражении (2.16) в каждой конституенте ж, на (х,- ф

ф 1). Применяя следующие тождества:

коммутативности

а ф /3 = /3 ф а;

ассоциативности

а ф (/? ф 7) = (а ф /3) ф 7;

дистрибутивности конъюнкции относительно сложения

по модулю 2

ос к (/3 ф 7) = (ак/З) ф (а к у); (2-17)

действия с константами

а ф а = 0, а ф 1 = а, а ф 0 = а, а ф а = 1;

получаем представление функции f(x i, х2, ..., х„) в виде

П П

/(х 1, Х2, . . ., Хп) = /о ф ^)''JfiiXj1 ф /ч<2 Ф • • •

п *’i= 1 *>i= 1

• • • Ф fi\ 12 ■ ■•Ifc *^11 • . *Х%к ф . . .

• • • ф fl2...nxl *2 • • •*„, (2.18)

124

Гл. 2. Математическая логика

где fo, ft! , /t'it2 ) • ' •) • • ■> Л 2...П — 0) 1) Н) ^2) • • •) € {0,

1, ..., п}, индексы (н, г2, . . й) попарно не равны друг другу,

что в дальнейшем обозначаем как ®(ii, i2, ..., ifc).

Выражение (2.18) называется полиномом Жегалкина функ

ции f(x 1, х2, ..., хп).

Последовательно продифференцируем полином Жегалкина

функции f(x 1, X2, ..., хп) по переменным х\, х2, ..., Xk и опреде

лим значение этой производной в точке 00.. .0. Учитывая, что

d ( / e <р) =

дх дх ® дх ’

ik{kxi) =i-k#xj'

после дифференцирования по переменным хх, х2,

dkf

(2.19)

(2.20)

Xk получаем

дх\дх2 .. .дхк

00...0

Действительно, после дифференцирования по переменным хх,

х2, ..., Xk все члены разложения в выражении (2.18) до f i2..,k

обращаются в 0, а в результате подстановки Xk+\ = Xk+2 = • • •

... = хп = 0 остальные члены этого разложения, кроме f\2...k, так

же будут равны 0. Отсюда получаем теорему о разложении любой

булевой функции f{x i, х2, ..., х„) в точке 00.. .0.

Т еор ем а 2.3. Любая булева функция f(x i, х2, ..., хп) пред

ставима своим значением в точке 00.. .0 и значениями всех

производных

d f d2f dnf

дх-ч ’ дх^ дх{2 ’ ' dxi дх2 ... дхп

в этой точке в виде

П Г\ £

f(x 1, x2t ..., хп) = / ( 0, 0, ..., 0) 0

d2f

^ д х {

dxidxj

00...0

& XiXj 0.

00...0

dkf

i,,-, ,ч-1 0*12 •••Я**

dnf

dxi dx2 .. .dxn

00...0

кх ix2...xn, (2.21)

00...0

*1) *2) • • •> t'fc) • • •> *n € {1, 2, . . ., n}, ®(*1) *2) • • •) • • •) ^n)*

§2.6. Разложение функции в заданной точке пространства 125

Пример 2.10. Найдем разложение булевой функции

/(х 1, х2, Хз, = V(0, 2, 4, 6, 13)

в точке 0000.

Вычисляем производные первого порядка и смешанные производные от бу

левой функцнн f(x 1, Х2, Хз, *4):

J ^7 = /(х; = 1) © /(х, = 0);

i = 1, f{x 1 = 1 )= х 2£зх4, _ _ _ _ _

fix i = 0 ) = X2X3X4 V X2X3X4 V Х2Г3Х4 V £2X3X4 = X4,

9 / —

----

_ _ _ _

—

---

= X2X3X4 © X4 = X2X3X4 • X4 V X2X3X4 • X4 = X4 V X2X3;

9xi

i = 2, /(x j = 1) = X1X3X4 VX1X3X4 V X1X3X4 = X1X4 V X1X3X4,

/ ( x 2 = 0 ) = X1X3X4 V X lX 3X4 = X lX 4 ,

9 / _ _ 4 _ _

= (X1X4 V X1X3X4) ФХ1Х4 = X1X3X4;

t = 3 , / (x 3 = 1) =XlX2X4 VX1X2X4 = X lX 4,

/ ( x 3 = 0 ) = X1X2X4 V X1X2X4 V x 1X2X4 = X1X4 V 11X2X4,

О /

= X1X4 © (X1X4 V Х1Г2Х4) = Х1Х2Г4;

i = 4 , /(x 4 = 1) = X1X2X3,

/(x 4 = 0) = X1X2X3 V X1X2X3 V X1X2X3 V X1X2X3 = xi,

df _ _

------

---

—— = X1X2X3 ® x\ = X1X2X3 • x\ V X1X2X3 • xi — xi V X2X3.

С/Х 4

Вычислим вторые смешанные производные д2 f /(Эх, dxj):

« = 1, 3 = 2,

9*/

9xi 9x2 9X2

92/

9xi 9хз

9xj

9*/

9xi 9x4

9xi

9*/

9x2 9хз

9хз

9*/ 9

9x2 9x4

9X4

9*/

9хз 9x4

9x4

( l £ ) =(_*4V_Z3)®*4 =

= X4 V X3 • X4 V (X4 V X3) • X4 = X3X4;

(£)-

i = 2, j = 3, — = xix4;

‘ 4> я - я- a . ( Эха) Х1Я3’

. = 3, j = 4, " = ~5~~ ( jr ~ ) = Д1Д2.

126

Гл. 2. Математическая логика

Вычислим третьи смешанные производные Э3//(Эх; Эху Эх*):

_ Э3/

___

Э_ / а2/ \_

* J ^ — 3, 8x18x28x3 дх\ \dx2dx3) Х*'

i = 1, j = 2, fc = 4,

» = 1, j = 3, fc = 4,

= 2, > = 3, * s 4,

Э3/ _ _Э_ / 32/ \ _ _

8x18x28x4 dxi \ Эхг3x4/ 13 ’

э3/ ^ a / a2/ \ .

8x18x38x4 dxi \dx3dx4 J 2’

a3/ a / a2/ \ =

3x2 8x3 8x4 3x2 \ 8x3 3x4 J 1

Наконец, четвертая смешанная производная 8*f /(8x18x28x38x4) имеет

вид

З4/ 3

8x18x28x38x4 Эи \dx2dx3dx4 d

Производные

з/ з/ а2/ а2/ а2/ а2/ а2/

3x 2 ’ Зхз ’ 3xi 3x 2 ' 3xi Зхз 3x2 Зхз ’ 3X2 3x4 ’ Эхз Эх4 '

а3/ а3/ а3/

3xi 3x2 Зхз ' 3xi Зхз 3x4 ’ 3*2 Зхз 3x4

в точке 0000 равны нулю, остальные — единице.

Согласно выражению (2.21) имеем разложение рассматриваемой булевой

функции в точке 0000 в виде

/ ( X 1, Х2, Хз, Х4) = 1 © Xl ® Х4 © Х1Х4 © X1X2X4 ф X1X2X3X4.

Для получения разложения булевой функции в ряд, аналогич

ный ряду Тэйлора в точке <т\сг2• введем новые координаты х[

х'2, ..., х'п, где х\ — х,ф<г,', * = 1,2, ..., п. Тогда точка сг\о2. • -сгп,

в координатах хх, х2, • ■ хп будет соответствовать точке 00.. .0

в координатах х\, х2, ..., х'п. Используя разложение (2.21) буле

вой функции в точке 00.. .0 в координатах а^, х2, ..., х'п и заме

няя каждую переменную zj. на х,- фа,-, * = 1, 2,..., п, получаем

теорему о разложении булевой функции f(x 1, х2, . . х„) в точке

<Т\СГ2. ..сгп-

Т еорем а 2.4. Любая булева функция f(x 1, х2, ..., хп) оп

ределяется своим значением в точке сг\а2...а п и значениями

всех своих производных

d f d2f dnf

dxix ’ dxix dxi2 ’ " dxi dx2 ... dxn

§2.7. Исчисление высказываний 127

в этой точке согласно выражению

dkf

dxh dxi2 ...dx{i

• к t r i o ? . ..О п j 1

& {Xij 0 &tj) 0 • • •

.......

*fc = l

« l / « 2 ..........

dnf

&(а:,-0 <г,-); (2.22)

*li *2) • • •> • • ■) in £ {1| 2, . . n}, ®(*1, *21 • • •) *fci • • •) *n)‘

Найдем разложение рассматриваемой булевой функции f(x\,

Х2, хз, х4) в точке 1010. Производные

df df df d2f d2f d2f d2f d2f

dx2 dx3’ dx4’ dxi dx2' dxidx3’ dx2dx3’ dx2dx4’ dx3dx4’

равны нулю в точке 1010, остальные — единице.

Согласно теореме 2.3 имеем разложение булевой функции в

виде

f(xu х2, хз, х4) = (xi 0 1) 0 (®i 0 1) • х4 0 х2 ■ (х3 0 1) • х4 0

0 (*1 0 1) • х2(хз 0 1) • Х4 = Xl 0 Х1Х4 0 Х2Х3Х4 0 Х\Х2ХзХ4.

Исчисление высказываний как формальную теорию можно оп

ределить с помощью аксиоматического метода.

Аксиоматическая (формальная) теория Т считается опреде

ленной, если выполнены следующие условия:

1) задано некоторое счетное множество, т. е. множество,

элементы которого могут быть взаимно однозначно сопоставлены

элементам натурального ряда 1, 2, ... символов — символов те

ории Т. Конечные последовательности символов теории называ

ются выражениями теории Т\

d3f d3f d3f

dx 1 dx2 dx3 ’ dxi dx2 dx4 ’ dx 1 dx3 dx4

§ 2.7. Исчисление высказываний

128

Гл. 2. Математическая логика

2) имеется подмножество выражений теории Т, называемых

формулами теории Т (формулы теории Т часто называют пра

вильно построенными формулами). Чтобы определить, является

ли выражение формулой в теории, существует эффективная про

цедура;

3) выделено некоторое множество формул, называемых аксио

мами теории Т;

4) имеется конечное множество R i, R2,. ■., Rn отношений меж

ду формулами, называемых правилами вывода. Для каждого Д,

существует натуральное j такое, что для всякого множества, со

стоящего из j формул, и для всякой формулы F эффективно ре

шается вопрос о том, находятся ли данные j формул в отношении

Ri с формулой F, и если да, то F называется непосредственным

следствием данных j формул по правилу Ri.

Выводом в Т называется всякая последовательность Fi,

F2, ■ ■ ■, Fm формул такая, что для любого г формула F, есть либо

аксиома теории Т, либо непосредственное следствие каких-либо

предыдущих формул.

Формула F теории Т называется теоремой теорий Т, если су

ществует такой вывод в Т, в котором последней формулой является

F; этот вывод называется выводом формулы F. В общем случае

может не существовать эффективной процедуры, с помощью кото

рой можно определить по данной формуле, существует ли ее вывод

в теории Т.

Формула, для которой такая процедура существует, называется

разрешимой в этой теории, в противном случае — неразрешимой.

Иначе говоря, для неразрешимых формул нельзя построить ал

горитм выяснения свойства формулы быть теоремой, для этого

требуются все новые и новые озарения (изобретательства), не под

дающиеся формализации.

Используя понятие аксиоматической теории Т, определим ис

числение высказываний в дизъюнктивном базисе Буля.

1. Символами теории Т являются V, , (, ) и буквы т,- с це

лыми положительными числами в качестве индексов: mi, m 2, ...

Символы V, называются связками, а буквы т,- — пропозицио

нальными буквами.

2. а) Все пропозициональные буквы являются формулами;

б) если А п В — формулы, то (AvB) и (Л) — также формулы;

в) выражение является формулой тогда и только тогда, когда

это может быть установлено с помощью п. а) и б).

Таким образом, всякая формула исчисления высказываний

есть некая пропозициональная формула, построенная из пропози

циональных букв с помощью связок V и

§2.7. Исчисление высказываний 129

3. Каковы бы ни были формулы А, В, С теории Т, следующие

формулы есть аксиомы Т :

А V А А, А V В В V А,

А А V В, (B -» C )-* (A V B -» A V C '),

j-де запись и а -> /3 эквивалентна записи а V /3.

4. Правила вывода исчисления высказываний следующие.

Правило подстановки: если а — выводимая формула и вме

сто любой переменной в этой формуле всюду произвести подста

новку любой формулы, то новая формула также является выводи

мой.

Правило заключения: если а —► /3 и а — выводимые формулы,

то /3 также выводимая формула;

Например, если высказывания А и А -> (д -> А) истинны, то

высказывание g А также является истинным согласно правилу

заключения.

Аналогично можно определить и другие булевы алгебры:

алгебру Вебба А = (М , о);

алгебру Шеффера А — (М , |);

импликативную алгебру А = (М, — 0);

коимпликативную алгебру А = (М , ->*►, 1);

алгебру Жегалкина А = (М, &, ®, 1).

Логический вывод широко используется в современных информационных

технологиях при разработке экспертных систем. Рассмотрим механизм логи

ческого вывода иа примере прогнозирования месторождений полезных ископае

мых.

Пусть геологическая партия после изучения одного из районов Тянь-Шаня

получила апостериорную информацию вида:

fi — если обнаружен крутопадающий сфалерит, то имеем нерудное тело;

/з — азимут падения доломита равен 180°;

/з — интервал угла падения рудного тела, содержащего барит, равен 35-60°;

ft — пологое залегание кальцита имеет азимут падения 300 ;

fs — галенит имеет азимут падения 160°;

/в — полезное ископаемое с крутопадающим залеганием и азимутом падения

от 5° до 270° является рудным телом;

/7 — азимут падения, равный 271-360°, имеют рудные тела или крутопа

дающие полезные ископаемые;

/в — пологое залегание нерудного тела имеет азимут падения 320°.

Цель геологоразведки — прогнозирование месторождения рудного тела.

Априорная информация по этому району:

— крутопадающим залеганием считается залегание с углом падения, превы

шающим 30°;

— результат минерализации нерудного тела — доломит, барит, кальцит;

— рудная минерализация представлена преимущественно галенитом и сфа

леритом, причем последний нередко образует обособленные залежи.

Обозначим первичными термами: ц — рудное тело, ®i — нерудное тело;

хг — галеннт, сфалерит; хз — доломит, барит, кальцит.

Угол падения: хз — пологое залегание (0-30°), хз — крутопадающее за

легание (свыше 30°); азимут падения: *4 — от 271° до 360°, х* — от 0°

до 270°.

5 В. А. Горбатов

130

Гл. 2. Математическая логика

Секвенцией называется высказывание, записываемое в виде F Ф, где

F — конъюнкция формул {fi}, Ф — дизъюнкция формул {<?]}, & fi -¥ V

и читаемое неформально как “F влечет Ф” или формально — “F имплици

рует Ф”.

Левая часть секвенции называется антецедентом (посылкой), правая —

сукцедентом (консеквентом, заключением). Эти термины являются терми

нами схоластической логикн.

Используя введенные обозначения х,, х,, t = 1, ..., 4, и секвенциальное

исчисление, апостериорную информацию запишем в следующем виде:

/ l = Х2Хз -* xi, h = X 2-bXA, / 3 = X lX 2 -» Х3, /4 = Х2Х3 Х4,

h = XI Х4, /б = Х3Х4 -+ X I, /7 = Xi V Ха -» Х4, /в = х и з Ч х 4.

Система секвенций {/,} несовместна, если антецедент этой системы & /,

тождественно равен нулю. '

В пространстве P(xi, xj, хз, Х4) характеристические векторы секвенций /,

имеют вид:

/l(x i, Х2 , хз, х4) — 1111111111110011,

h(xi, Х2 , хз, х4) — 101011111010 1111,

/з(Х 1, Х2, Хз, х4) — 1111 1111 1100 1111,

Ы х и Х2, хз, х4) — 1101 1111 1101 1111,

/six 1, Х2 , хз, Х4) — 11111010 1111 1010,

/в(Х1, Х2, хз, х4) — 01110111 1111 1111,

/ 7 (х 1, Х2 , хз, Х4 ) — 0111 01110101 0101,

/ 8(х 1 , Х2, ХЗ, х4) — 1101 1101 1111 1111,

где каждый характеристический вектор представляет собой значения соответ

ствующей функции /;(х 1, Х2, хз, Х4 ) в точках 0, 1, 2, ..., 15.

Антецедент

& / , =0000000000000000

равен нулю, следоват.ельно, секвенциальная система {ft} противоречива. Для

порождения всех непротиворечивых секвенциальных систем, используя свойство

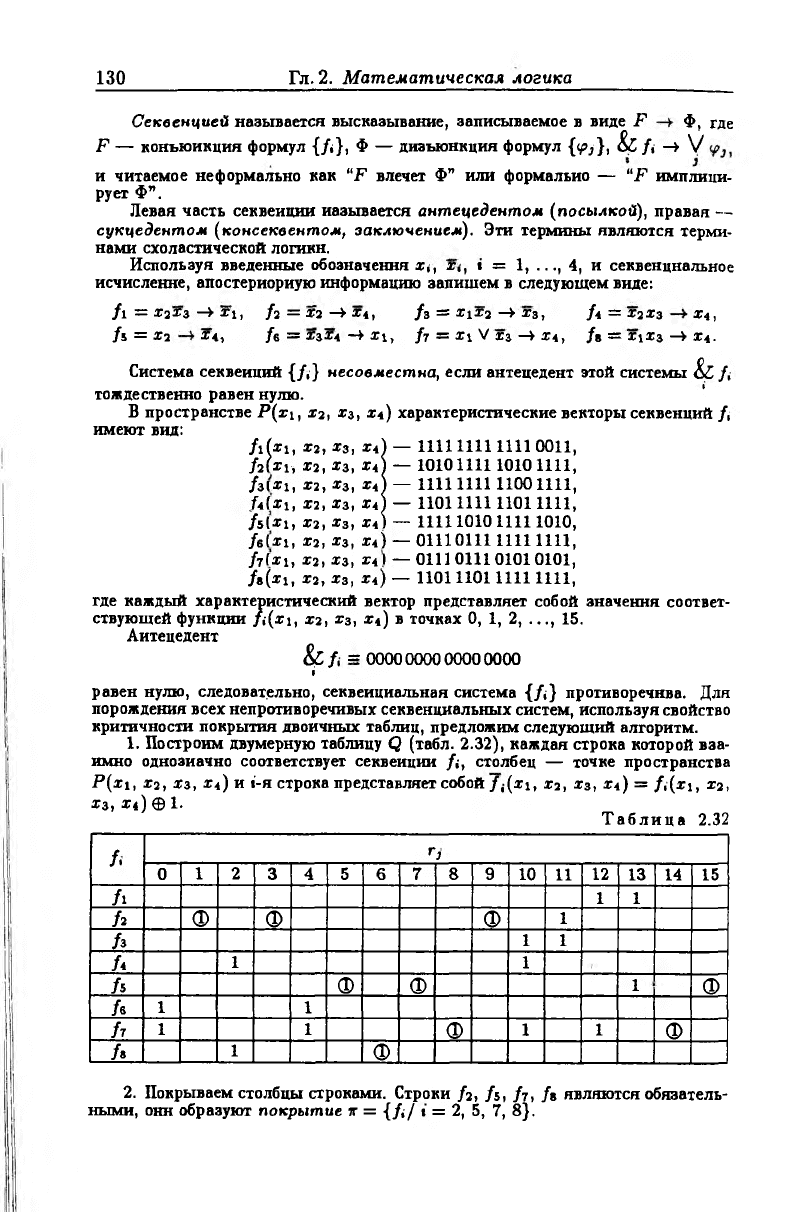
критичности покрытия двоичных таблиц, предложим следующий алгоритм.

1. Построим двумерную таблицу Q (табл. 2.32), каждая строка которой вза

имно однозначно соответствует секвенции /;, столбец — точке пространства

P(xi, Х2, хз, Х4) и i-я строка представляет собой/,(x i, х2, хз, Х4) = / ,(х 1, хг,

Хз, Х4) ® 1.

Т аблица 2.32

Г1

1 2

3 4 5 6 7 8 9

13 14 15

1 1

Ф Ф

/з

1 1

Ф Ф

1 1

2. Покрываем столбцы строками. Строки / 2, /5, /7, /в являются обязатель

ными, онн образуют покрытие v = {/</ г = 2, 5, 7, 8}.