Глущенко А.Г., Головкина М.В. Физические основы волоконной оптики. Конспект лекций
Подождите немного. Документ загружается.

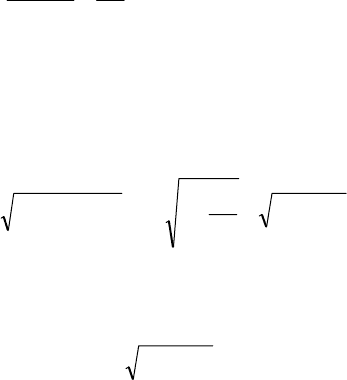
ления для границы раздела воздух-сердцевина волокна (точка
А):
0
1
кр
m
n
n
sin
sin
=
θ
Ω
. (8.5)
Здесь показатель преломления воздуха. Будем считать
. Угол находим по формуле (7.6):
0
n-
1n
0
=
кр
θ
12кр
n/ncos =θ .
Найдем из (8.5):
m
sin Ω
2
2
2
1
2
1
2
2
1кр
2
1кр1m
nn
n
n
1ncos1nsinnsin −=−=θ−=θ=Ω
.
Величину называют
числовой апертурой волокна. Чи-
словая апертура имеет обозначение NA. Таким образом, число-
вая апертура равна
m
sin Ω
2
2
2
1m
nnsinNA −=Ω= . (8.6)
Числовая апертура волокна определяет максимальный угол
ввода в волокно луча, который будет испытывать полное
отражение и распространяться в волокне
.
Если условие (7.6) полного отражения не выполняется, то
будут распространяться лучи с утечкой или преломленные лучи.
Более подробную информацию об этих лучах можно найти в
книге [2].
8.3. Градиентное волокно. Числовая апертура
Рассмотрим градиентное оптическое волокно (см. рис. 8.3).
Его показатель преломления, в отличие от ступенчатого волок-
на, меняется при изменении r (см. 8.2):
⎩
⎨
⎧
≥=
<=
.arесли,nn
,arесли,)r(nn
2
Аналогично ступенчатому волокну, можно найти максимальный
угол вода излучения в волокно, только он будет зависеть от рас-
71

стояния r: . Величину )назовем локаль-
ной числовой апертурой волокна
:
)r(
mm
Ω=Ω r(sin
m
Ω
2
2
2
m
n)r(n)r(sin)r(NA −=Ω= . (8.7)
Любой луч, падающий на торец волокна на расстоянии r от оси
и попадающий внутрь апертурного конуса с углом при вершине
, испытывает после ввода полное отражение и рас-
пространяется в волокне. Локальная числовая апертура
максимальна на оси волокна и падает до нуля на границе
сердцевина и оболочки.
)r(
m
Ω
Числовой апертурой градиентного волокна будем назы-
вать максимальной значение локальной числовой аперту-
ры
.
Для градиентного волокна с квадратичным профилем пока-
зателя преломления (формула (5.8)) определяется эффективная
числовая апертура, которая равна:
2
n)0(n
NA
2
2
2
eff
−
=
. (8.8)
8.4. Мощность, вводимая в волокно
Покажем, что только часть света, излучаемая малоразмер-
ным диффузным источником, помещенным на оптической оси
волокна вблизи его торца, может быть введена в волокно.
Рассмотрим малоразмерный диффузный источник света, яркость
которого одинакова во всех направлениях, изображенный на
рисунке 8.8. Пусть - мощность, излучаемая в единицу телес-
ного угла по нормали к источнику, - мощность,
излучаемая под углом θ. Тогда мощность, излучаемая в малый
телесный угол , равна
0
I
θ=θ cosI)(I
0
Ωδ
δθθπθ=δθθ sin2cosIcosI
00
.
72
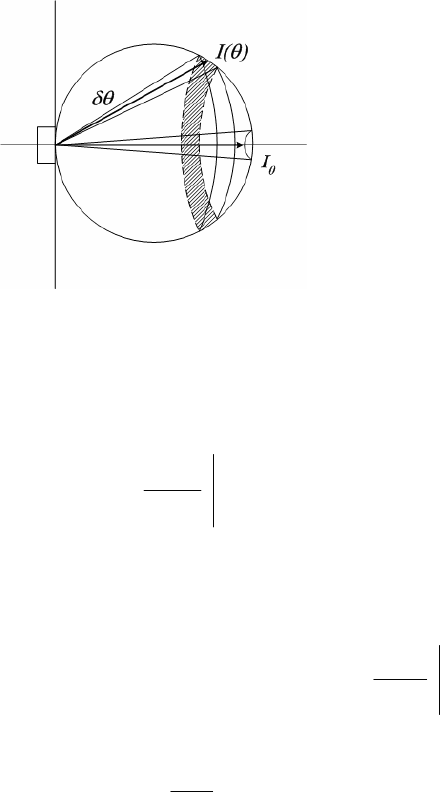
Рис. 8.8. Диффузный ис-
точник света.
Полная мощность, излучаемая таким источником, находится
интегрированием этого выражения по всем направлениям:
()()()
.I
2
sin
I2
)(sindsinI2dsin2cosIФ
0
2/
0
2
0
2/
0
0
2/
0
00
π=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
θ
π=
=θθπ=θθπθ=
π
=θ
ππ
∫∫
(8.9)
Мощность, введенная в волокно, диаметр сердцевины кото-
рого больше диаметра источника, определяется следующим ин-
тегралом:
()()()
()
.NAФsinI
2
sin
I2dsin2cosIФ
2
0m
2
0
m
0
2
0
m
0
0
=Ωπ=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
θ
π=θθπθ=
Ω
=θ
Ω
∫
(8.10)
()
2
m
2
0
NAsin
Ф
Ф
=Ω=
.
Мы видим, что мощность, вводимая в волокно, зависит от
числовой апертуры волокна NA
. Преобразуем выражение для
числовой апертуры:
73
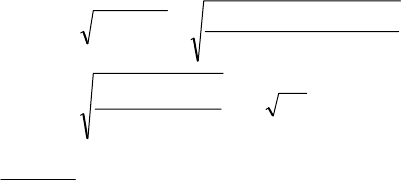
,2n
n
)nn(n2
n
n)nn)(nn(
nnNA
1
1
21
2
1
1
12121
2
2
2
1
Δ=
−
≈
≈
+−
=−=
(8.11)
2
1
2
2
2
1
n2
nn −
=Δ
где
-
относительная разность показателей пре-
ломления.
Отсюда ясно, что для того чтобы ввести в волокно как можно
больше света, необходимо обеспечить большие значения вели-
чин и . Очевидно, что лучшее, что может быть сделано –
это использовать для изготовления волокна стекло с большим
показателем преломления и не покрывать его оболочкой. Одна-
ко при этом наряду с увеличением мощности, вводимой в во-
локно, возникают две проблемы:
Δ
1
n
1.
Часть волны даже при полном внутреннем отражении
проникает наружу сквозь отражающую поверхность. А
неизбежное наличие неровностей и неоднородностей на
ней преобразует затухающую в воздухе волну в распро-
страняющуюся, что приводит к большим потерям.
2.
При увеличении увеличивается межмодовая диспер-
сия, что приводит к искажению сигнала.
Δ
8.5. Траектория световых лучей
а) Ступенчатое волокно.
Показатель преломления сердцевины ступенчатого волокна
есть постоянная величина. Угол θ, под которым луч распро-
страняется в волокне, является постоянным. Луч распространя-
ется, испытывая полное отражение на границе раздела сердце-
вина-оболочка. Между двумя последовательными полными от-
ражениями траектория луча прямолинейная.
1
n
74
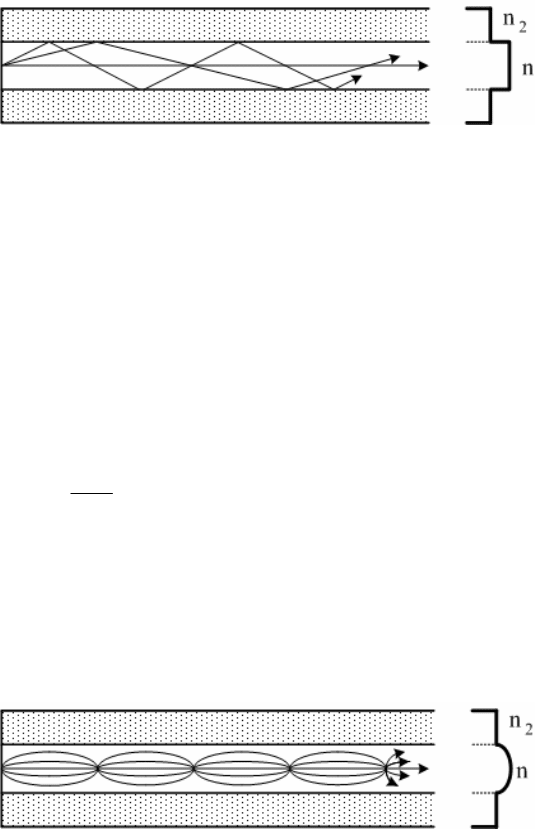
Рис. 8.9. Траектория лучей в ступенчатом многомодовом волок-
не.
Траектория состоит из равных отрезков, получаемых один из
другого путем смещения вдоль оси Oz на определенное рас-
стояние и поворота на угол ψ вокруг оси Oz. В поперечной про-
екции они касаются одной и той же окружности радиусом R.
б) Градиентное волокно.
Из-за того, что показатель преломления сердцевины меняет-
ся, траектория лучей в градиентном волокне носит сложный ха-
рактер и зависит от конкретного вида зависимости ). В част-
ном случае волокна с квадратичным показателем преломления
r(n
)r
n2
n
1(nn
2
0
2
0
−=
траектория луча в поперечной проекции
представляет собой замкнутую кривую (эллипс). В продольном
разрезе траектории являются плавными линиями (рис. 8.10).
Особенностью такого градиентного волокна является то, что
оптические длины путей для всех лучей одинаковы, что соот-
ветствует отсутствию межмодовой дисперсии.
Рис. 8.10. Траектория лучей в градиентном волокне
75
Выводы
Рассмотрены типы оптических волокон. На основе закона
преломления ведено понятие числовой апертуры. Показано, что
мощность, вводимая в волокно, зависит от величины числовой
апертуры. Для случаев, допускающих лучевую трактовку, рас-
смотрен ход лучей в оптических волокнах.
Вопросы и задачи
8.1. Что такое сердцевина оптического волокна? Оболочка? Ка-
кие преимущества дает покрытие волокон оболочкой?
8.2. Какие волокна называются ступенчатыми? Градиентными?
8.3. Какой показатель преломления больше: сердцевины или
оболочки? Почему?
8.4. Что такое числовая апертура для ступенчатого волокна?
Выведите формулу для ее расчета.
8.5. Как определяется числовая апертура для градиентного во-
локна? Что такое локальная числовая апертура?
8.6. От чего зависит мощность излучения, вводимая в волокно?
Как можно увеличить эту мощность? Почему такое увели-
чение мощности нецелесообразно?
8.7. Опишите вид траектории при распространении лучей в сту-
пенчатом волокне и в градиентном волокне (для случая,
когда применима лучевая трактовка).
8.8. К чему приводит увеличение разности показателей прелом-
ления ? Почему изготавливают волокна с очень
малыми значениями разности показателей преломления
? (Указание: более подробное рассмотрение во-
проса будет дано в лекции № 10 при изучении межмодо-
вой дисперсии).
21
nn −
21
nn −
8.9. Вычислите значения числовой апертуры NA и максималь-
ного угла ввода излучения в волокно для ступенчато-
го волокна с параметрами а) , ; б)
, .
m
Ω
483,1n
1
= 479,1n
2
=
483,1n
1
= 460,1n
2
=
76
ЛЕКЦИЯ 9
Решения уравнений Максвелла для оптического во-
локна. Число мод в оптическом волокне.
9.1. Моды распространения в оптическом волокне.
Формулы для полей
В случае световых лучей, распространяющихся в идеальном
волокне, потери отсутствуют. Мы установили условия ввода,
нашли постоянную распространения, рассмотрели траекторию
лучей в ступенчатом и градиентном волокне. Однако необходи-
мо помнить, что в реальном волокне наряду с волной, распро-
страняющейся в сердцевине, существует волна, распростра-
няющаяся в оболочке, причем это волна той же фазы. Если ме-
няются условия распространения в оболочке, то меняется рас-
пространение света и в сердцевине. Например, если у двух сред
разный коэффициент поглощения (а на практике так обычно и
бывает), то в одной из них волна будет затухать быстрее, и рас-
пространение будет нарушено! Даже при одинаковом поглоще-
нии чисто геометрическая оптика не позволяет оценивать поте-
ри, обусловленные лучами утечки, для этого необходимо знать
выражение для полей в сердцевине и в оболочке. Таким обра-
зом, в некоторых случаях нужно рассчитывать электромагнит-
ное поле в волокне.
Запишем волновое уравнение в комплексной форме для изо-
тропной среды, в которой отсутствуют токи и заряды:
.0k
,0
22
22
=+∇
=+∇
HH
EkE
(9.1)
По-прежнему, мы рассматриваем распространение волны в во
будут присутствовать продольные компоненты полей
и
то есть в волокне будут распространяться гибридные волны.
Используем цилиндрическую систему координат. Из уравнений
(9.1) получится шесть скалярных уравнений. Будем искать ре-
шение этой системы уравнений в виде гармонических функций
переменной z. Зависимость от времени по-прежнему останется
экспоненциальной:
. Итак, решение волнового уравнения
ищем в виде произведения:
z
E
z
H,
ti
e
ω
77

zi
21z
e)()r(E
β−
⋅ϕψ⋅ψ= , (9.2)
где - постоянная распространения (продольное волновое чис-
ло), r,
ϕ и z - цилиндрические координаты. В аналогичной форме
ищем решение и для Н.
β
Решение уравнений (9.1) является достаточно слож-
ным. Поэтому мы приведем результат решения без выво-
да. Более подробное описание можно найти в [1] и [2]. Чи-
татель, не желающий вникать в подробности вывода, мо-
жет сразу перейти к разделу "Решение волнового уравне-
ния для ступенчатого волокна".
Итак, подставляя (9.2) в (9.1) и разделяя переменные,
получаем отдельные уравнения для радиальной состав-
ляющей )
r(
1
ψ
и для азимутальной составляющей )(
2
ϕ
ψ
:
0)
r
nk(
rd
d
r
1
rd
d
1
2
2
222
1
2
1
2
=ψ
ν
−β−+
ψ
+
ψ
, (9.3)
Решение для азимутальной составляющей имеет вид
ϕν
=ϕψ
i
2
e)( . (9.4)
Здесь
ν - некоторая константа, которая определяется на-
чальными условиями падения луча на оптоволокно:
00
sinrsink
ϕ
Ω
=
ν
, (9.5)
где -угол, под которым свет падает на торец оптоволок-
на, - расстояние от оси волокна до точки падения луча
на торец,
Ω
0
r
0
ϕ
- угол между радиус-вектором, проведенным
от центра волокна к точке падения луча на торец, и следом
плоскости падения.
Решения ищем для компонент полей и , а ос-
тальные компоненты выражаем через них, используя со-
отношения
z
E
z
H
)
H
rr
E
(
i
E
zz
2
r
ϕ∂
∂
μ
ω+
∂
∂
β
χ
−= ,
)
r
HE
r
(
i
E
zz
2
∂
∂
μω−
ϕ∂
∂
β
χ
−=
ϕ
,
78

)
E
rr
H
(
i
H
zz
2
r
ϕ∂
∂
μ
ω−
∂
∂
β
χ
−= , (9.5)
)
r
EH
r
(
i
H
zz
2
∂
∂
ε+
ϕ∂
∂
β
χ
−=
ϕ
.
Решения волновых уравнений должны удовлетворять гра-
ничным условиям. Накладываемое волокном граничное
условие следует из закона изменения показателя прелом-
ления ). Решения также подчиняются требованиям,
чтобы поля были конечными на оси волокна и обращались
в нуль на бесконечности. Эти условия обусловливают ре-
шения в собственных значениях для )
r(n
,r(
ϕ
ψ
, каждое из ко-
торых имеет конкретное значение постоянной распро-
странения
β
. Это приводит к дискретным картинам рас-
пространяющихся в волокне электромагнитных волн или
мод.
Решение волнового уравнения для ступенчатого волокна
Рассмотрим ступенчатое волокно. Показатель преломления
меняется по следующему закону
⎩
⎨
⎧
≥=
<=
.arесли,nn
,arесли,nn
2
1
Решения уравнений (9.1) для сердцевины записываются через
хорошо известные функции Бесселя:
:a
r
<
ϕν
ν
⎟
⎠
⎞
⎜
⎝
⎛
=
i
z
e
a
r
uJAE,
ϕν
ν
⎟
⎠
⎞
⎜
⎝
⎛
=
i
z
e
a
r
uJBH
, (9.6)
222
1
2
0
2
a)nk(u β−= .
Здесь
⎟
⎠
⎞
⎜
⎝
⎛
ν
a
r
uJ
- функция Бесселя первого рода, c/k
0
ω
=
,
а - радиус сердцевины.
Решения для оболочки:
79

:a
r
≥
ϕν
ν
⎟
⎠
⎞
⎜
⎝
⎛
=
i
z
e
a
r
wKCE,
ϕν
ν
⎟
⎠
⎞
⎜
⎝
⎛
=
i
z
e
a
r
wKDH , (9.7)
22
2
2
0
22
a)nk(w −β=
.
Здесь
⎟
⎠
⎞
⎜
⎝
⎛
ν
a
r
wK
- модифицированная функция Ганкеля.
Постоянные А, В, С, D находятся из граничных условий. Гра-
ничные условия, накладываемые на компоненты , ,
на границе раздела сердцевина-оболочка, приводят к тому,
что для каждого значения параметра существует только опре-
деленный дискретный набор значений u и w. Обозначим их
и . k и m являются целыми числами. Соответственно по-
стоянная распространения
z
E
ϕ
E,
z
H
ϕ
H
ν
km
u
km
w
β
также принимает только дискрет-
ные значения. Таким образом, решения (9.6) и (9.7) для ступен-
чатого волокна представляют собой моды, зависящие от номе-
ров k и m.
-0,5
0
0,5
1
0 2 4 6 8 10 12 14
J
0
J
1
J
2
J(v)
v
Рис. 9.1. График функций Бесселя низких порядков.
80
