Глущенко А.Г., Головкина М.В. Физические основы волоконной оптики. Конспект лекций

Преимущества от применения волоконно-оптических

линий связи (ВОЛС) настолько значительны, что в настоящее

время эти линии связи очень широко используются для переда-

чи информации.

1.2. Уравнения Максвелла

Запишем систему уравнений Максвелла, которые включают

в себя основание теории распространения электромагнитных

волн и являются постулатами теории:

,

t

rot

∂

−=

B

E

(1.1)

,

t

rot j

D

H +

∂

=

(1.2)

,0div =B (1.3)

.div

ρ

=D (1.4)

Здесь Е - вектор напряженности электрического поля, D - вектор

электрической индукции, В - вектор магнитной индукции, Н -

вектор напряженности магнитного поля, j - плотность тока про-

водимости, ρ - объемная плотность электрических зарядов.

Формулы (1.1)-(1.4) выражают уравнения Максвелла в диффе-

ренциальной форме.

Уравнения Максвелла дополняются следующими уравне-

ниями:

,

0

ED εε= (1.5)

,

0

HB

μ

= (1.6)

,

ст

jEj +σ= (1.7)

Здесь - электрическая постоянная,

0

ε

0

μ

-магнитная постоянная,

ε -диэлектрическая проницаемость среды, μ - магнитная прони-

цаемость среды, σ - удельная проводимость, j

ст

- плотность сто-

ронних токов. (В такой записи сторонние токи считаются задан-

ными. Они возбуждают поля, но не порождаются рассматривае-

мыми электромагнитными полями). Формула (1.7) является

дифференциальной формой записи закона Ома.

11

Значение уравнений Максвелла как оснований теории элек-

тромагнетизма чрезвычайно велико. Для инженера в первую

очередь важно, что уравнения Максвелла дают возможность ис-

следовать любые электромагнитные процессы.

1.3. Уравнения Максвелла в комплексной форме

Рассмотрим поля, меняющиеся по гармоническому закону:

).tcos(

,)tcos(

krHH

krEE

0

−ω=

−

ω

=

(1.8)

Здесь Е -напряженность электрического поля, Н- напряжен-

ность магнитного поля, k - волновой вектор, r - радиус-вектор

рассматриваемой точки.

Используем метод комплексных амплитуд. В рамках этого

метода векторам Е и Н приведем в соответствие комплексные

числа и . При этом

E

&

H

&

ti

e

ω

=

m

EE

&&

, (1.9)

.

ti

e

ω

=

m

HH

&&

Значения реальных векторов Е и Н находятся как действитель-

ные части соответствующего комплексного вектора:

,}e{Re

tiω

=

m

EE

&

(1.10)

.}e{Re

ti ω

=

m

HH

&

Величины и называются комплексными ампли-

тудами векторов Е и Н. Комплексные амплитуды зависят толь-

ко от пространственных координат и не зависят от времени:

m

E

&

m

H

&

)z,y,x(,)z,y,x(

mmmm

HHEE

&&&

==

Для обозначения комплексной амплитуды будем ставить точку

вверху и нижний индекс m.

Пример. Рассмотрим плоскую волну, распространяю-

щуюся вдоль оси Oz. Поставим в соответствие этой волне

комплексную амплитуду . Для перехода

ikz

e)z(

−

⋅=

0m

EE

&

12

к реальному вектору Е найдем действительную часть от

соответствующего комплексного вектора:

=⋅=⋅⋅=

−ωω−

}e{Re}ee{Re

)kzt(itiikz

00

EEE

)kztcos()}kztsin(i)kztcos({Re −

ω

=−

ω

−−

ω

=

00

EE .

В результате получилось хорошо известное уравнение

плоской волны, распространяющейся в положительном

направлении оси Oz.

В методе комплексных амплитуд операции дифференциро-

вания по времени соответствует умножению на iω:

ω→

∂

i

t

. (1.11)

Подставим комплексные представления (1.9) в уравнения Мак-

свелла. С учетом (1.11) уравнения Максвелла (1.1-1.2) можно

записать в комплексной форме:

,irot

mm

BE

&&

ω−= (1.12)

,irot

mmm

jDH +ω=

&&

(1.13)

где , , , , - комплексные амплитуды соответст-

вующих векторов. Решение уравнений Максвелла в комплекс-

ной форме зачастую является более простым, так как в записи

уравнений отсутствуют производные по времени. Для перехода

к наблюдаемым векторам Е и Н достаточно найти действитель-

ную часть соответствующего комплексного вектора.

m

E

&

m

B

&

m

H

&

m

D

&

m

j

Примечание. Комплексные амплитуды можно ввести и дру-

гим способом, сопоставляя векторам Е и Н комплексные числа

ti

e

ω−

=

m

EE

&&

, (1.14)

.

ti

e

ω−

=

m

HH

&&

Тогда в уравнениях Максвелла в комплексной форме изменятся

знаки перед множителем iω.

13

1.4. Комплексная диэлектрическая проницаемость

Преобразуем правую часть уравнения (1.13). Подставим

вместо плотности тока j

m

закон Ома в виде (1.7), заменяя векто-

ры Е и j комплексными амплитудами и j

m

E

&

m

:

=+

ωε

σ

−εεω=+σ+εεω=+ω

ст

mm

0

ст

mmm0mm

)i(iii jEjEEjD

&&&&

. (1.15) i

ст

mm0

jE +εεω=

&

Здесь введено новое обозначение:

- комплексная диэлектрическая проницаемость.

ε

&

ωε

σ

−ε=ε

0

i

&

(1.16)

или

ε

′′

−ε

′

=ε

&

,

где - действительная и мнимая часть комплексной ди-

электрической проницаемости соответственно.

ε

′′

ε

′

и

С учетом введенной комплексной диэлектрической прони-

цаемости (1.15) и с учетом связи векторов В и Н запишем урав-

нения Максвелла (1.12) и (1.13) в следующем виде:

,irot

0 mm

HE

&&

μμω−=

(1.17)

.irot

ст

mm0

jEH

m

+εεω=

&

(1.18)

Мы видим, что комплексная диэлектрическая проницае-

мость позволяет учесть зависимость электродинамических

свойств среды от частоты, то есть ее дисперсию. Одновременно

введение учитывает запаздывание вектора D относительно

вектора Е в высокочастотных электромагнитных полях.

ε

&

В общем случае наличие мнимой части у диэлектриче-

ской проницаемости говорит о наличии затухания в среде.

Действительно, через диэлектрическую проницаемость

ε

выражается волновой вектор k. Напомним: волновой вектор k

определяет направление распространения плоской монохрома-

14

тической волны. Модуль волнового вектора k называется вол-

новым числом

λ

π= /2k , (1.19)

где

λ - длина волны. Волновое число можно выразить также че-

рез фазовую скорость волны:

.v/k

ω

= (1.20)

Скорость распространения волны в среде находится следую-

щим образом:

n/cv = , (1.21)

где с - скорость света в вакууме, n - показатель преломления

среды.

В свою очередь,

με=n , (1.22)

где

ε и μ - диэлектрическая и магнитная проницаемость среды.

Таким образом, если

ε является комплексной, то и волновое

число k тоже будет комплексным:

.kik

c

k

′′

−

′

=με

ω

= (1.23)

Наличие мнимой части говорит о затухании волны в среде.

Действительная часть k' определяет фазовую скорость электро-

магнитной волны

k

′′

.k/v

ф

′

ω

= (1.24)

Пример. Рассмотрим плоскую волну, распространяю-

щуюся в положительном направлении оси Oz. Запишем

уравнение волны в комплексной форме:

)kzt(i

e

−ω

⋅=

0

EE

&

.

Учтем наличие у волнового вектора k действительной и

мнимой части, подставив выражение (1.23):

)zkt(izki

ee

′

−ω

′′

−

⋅=

0

EE

&

(1.25)

15

Множитель показывает, что волна экспоненциально

затухает с увеличением координаты z. Поэтому мнимую

часть

zki

e

′′

−

k

′′

иногда называют коэффициентом затухания.

Выводы

Применение уравнений Максвелла в комплексной форме во

многих случаях позволяют облегчить их решение за счет упро-

щения операции дифференцирования по времени и по простран-

ственным координатам. Введение комплексного волнового чис-

ла и комплексной диэлектрической проницаемости позволяют

учесть наличие потерь в среде.

Вопросы и задачи

1.1. Запишите уравнения (1.3) и (1.4) в комплексной форме. В

чем преимущество метода комплексных амплитуд?

1.2. Что такое волновой вектор?

1.3. Какие свойства среды позволяет учесть введение комплекс-

ной диэлектрической проницаемости?

1.3. Объясните, что определяют действительная и мнимая часть

волнового числа?

1.4. Выберите зависимость от времени в плоской волне в виде

. Запишите уравнения Максвелла (1.1 - 1.2) в ком-

плексной форме для данной временной зависимости. (Ука-

зание: сопоставьте векторам

Е и Н комплексные числа

, ).

ti

e

ω−

ti

e

ω−

=

m

EE

&&

ti

e

ω−

=

m

HH

&&

1.5. Найти параметры k' и k'' плоской однородной волны, рас-

пространяющейся в плавленом кварце на частоте 10

8

Гц

( , ).

8,3=ε м/Cм10

16−

=σ

ПРИМЕЧАНИЕ: в конце конспекта лекций приведены ответы

на некоторые вопросы, а также ответы ко всем задачам.

Некоторые задачи снабжены подробным решением.

16

ЛЕКЦИЯ 2

Волновые уравнения в комплексной форме. фазовая и

групповая скорость

2.1. Волновые уравнения в комплексной форме

Рассмотрим волновые уравнения, являющиеся прямым

следствием уравнений Максвелла:

.

tc

,

tc

2

∂

∂με

=∇

∂

∂με

=∇

H

E

(2.1)

Решением уравнений (2.1) является плоская электромагнитная

волна:

,)tcos(

0

rkHH

rkEE

−ω=

−

ω

=

(2.2)

где k - волновой вектор.

Запишем уравнения (1.21) в комплексной форме. При этом

вместо векторов Е и Н будут присутствовать их комплексные

амплитуды и , а вместо второй производной по време-

ни появится множитель -ω

m

E

&

m

H

&

2

(см.(1.11)) :

2

t

ω−→

∂

. (2.3)

Тогда

,

c

2

mm

EE

&&

εμω

−=∇

mm

HH

&&

2

c

εμω

−=∇

.

С учетом (1.23) волновые уравнения запишем в следующем ви-

де:

⎪

⎩

⎪

⎨

⎧

=+∇

. 0

, 0

22

mm

HkH

EkE

&&

(2.4)

17

2.2. Волновое сопротивление

Рассмотрим плоскую волну, распространяющуюся вдоль оси

Z. Параметры волны зависят только от координаты z и не зави-

сят от координат x, y, поэтому частные производные по х и у

равны нулю:0. Оператор Лапласа будет

иметь следующий вид: . Тогда уравнения (2.4) уп-

рощаются:

y/ ,0x/ =∂∂=∂∂

222

z/ ∂∂=∇

. 0

dz

d

,0

dz

d

2

=+

m

Hk

H

Ek

E

&

(2.5)

Общее решение дифференциальных уравнений (2.5) ищем в ви-

де суммы двух волн:

,DeCe

,BeAe

ikzikz

+−

−

+−

−

+=+=

mmm

HHH

EEE

&&&

(2.6)

где A, B, C, D - векторные константы. Волна

ikz

Be

−

+

=

m

E

&

(2.7)

распространяется в положительном направлении оси Oz, волна

(2.8)

ikz

Ae=

−

m

E

&

- в противоположном направлении. (То же справедливо для волн

и .)

+

m

H

&

−

m

H

&

Пусть отсутствуют сторонние токи: . Выразим из

уравнения Максвелла (1.17):

0

m

=j

m

E

&

mm

HE

&&

rot

i

0

εεω

−=

. (2.9)

Рассмотрим волну , распространяющуюся в положитель-

ном направлении оси Oz. Распишем операцию взятия ротора в

декартовой системе координат и учтем, что

+

m

E

&

0

y

,0

x

=

∂

=

∂

,

ik

z

−=

∂

:

18

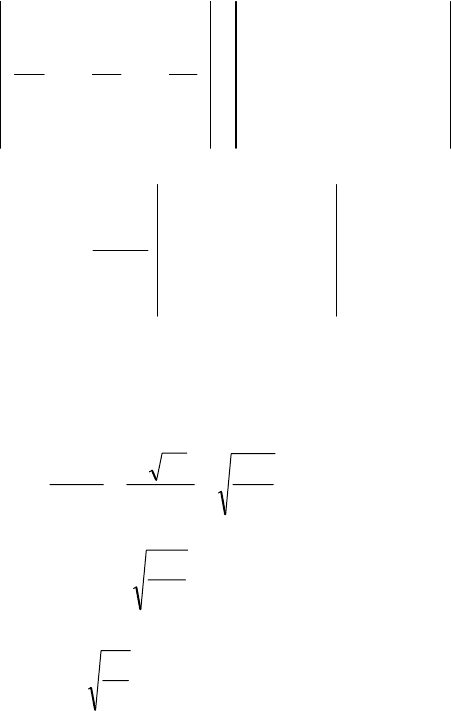
z

m

y

m

x

m

z

m

y

m

x

m

HHH

ik00

HHH

zyx

rot

+++

+

−=

∂

=

&&&&&&

&

kji

H

m

Тогда из (2.9):получаем:

z

m

y

m

x

m

0

HHH

100

k

+++

+

εεω

−=

&&&

&

kji

E

m

. (2.10)

Здесь k, стоящее в верхней строчке определителя, является ор-

том (единичным вектором) оси Oz, а k, находящееся перед оп-

ределителем, есть волновое число. Чтобы избежать путаницы,

ниже будем обозначать орт оси Oz символом z

0

.

Преобразуем

0

00

c

k

εε

μμ

=

ωεε

εμω

=

εωε

. (2.11)

Назовем волновым сопротивлением величину

0

Z

εε

μμ

=

. (2.12)

Волновое сопротивление вакуума (1 ,1 =ε=

μ

):

ом377120Z

0

≈π=

ε

μ

= . (2.13)

Для немагнитных сред (1=

μ

)

n/ZZ

0

=

, (2.14)

где n – показатель преломления среды.

С учетом введенного волнового сопротивления выражение

(2.10) можно записать в следующем виде:

],[Z

0mm

zHE

++

=

&&

, (2.15)

где z

0

- орт оси Oz.

19

Аналогично, используя волновое сопротивление, можно выра-

зить через

:

+

m

H

&

+

m

E

&

],[Z

++

=

m0m

EzH

&&

. (2.16)

Для волн, распространяющихся в направлении, противополож-

ном оси Oz, справедливы следующие соотношения:

],[Z

0mm

zHE

−−

−=

&&

. (2.17)

],[Z

−−

−=

m0m

EzH

&&

. (2.18)

Таким образом, волновое сопротивление можно записать как

отношение амплитуд напряженности электрического и магнит-

ного поля:

±

±=

m

H

E

&

Z

. (2.19)

2.3. Групповая скорость

Дисперсия - зависимость диэлектрической проницаемости

среды ε (а, следовательно, и показателя преломления n) от час-

тоты волны. Введение комплексной диэлектрической проницае-

мости

ωε

σ

−ε=ε

0

i

&

позволяет учесть дисперсию уже в силу

присущей среде электропроводности. Существование дисперсии

необходимо учитывать, оценивая распространение электромаг-

нитных сигналов, переносящих информацию. Плоская электро-

магнитная волна, не ограниченная во времени, не может быть

сигналом. Любой сигнал имеет начало и конец, то есть пред-

ставляет собой импульс, обладающий некоторым спектром час-

тот. В результате дисперсии различные частотные составляю-

щие импульса распространяются с разными фазовыми скоро-

стями, что приводит к искажению сигнала.

Воспользуемся для случая произвольной временной зависи-

мости разложением в интеграл Фурье:

ωω=

ω

∞

∞−

∫

de)(u)t(u

ti

&

. (2.20)

20

Глущенко А.Г., Головкина М.В. Физические основы волоконной оптики. Конспект лекций

Подождите немного. Документ загружается.