Глущенко А.Г., Головкина М.В. Физические основы волоконной оптики. Конспект лекций
Подождите немного. Документ загружается.

где Ом377Z
0
0
0
≈
ε
μ
= - волновое сопротивление вакуума,
εε
μμ
=
0
0
Z - волновое сопротивление среды.
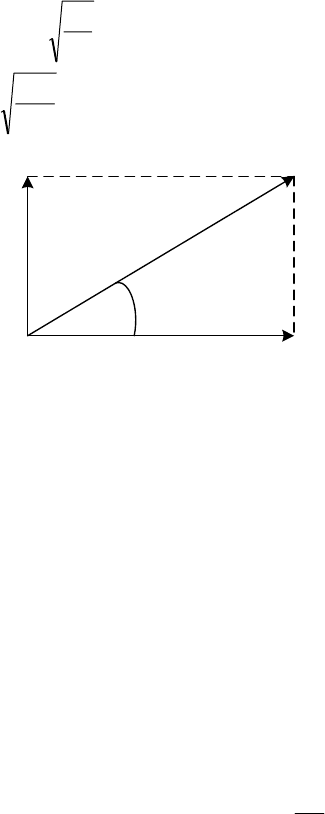
Если α - угол между на-
правлением колебаний
вектора
Е
пад
в падающей
волне и плоскостью паде-
ния (см. рис 3.3), то пер-
пендикулярная и парал-
лельная составляющие
выражаются следующим
образом
пад
E
⊥пад
E
||пад
E
α
Рис. 3.3.
α=
⊥
sinЕE
падпад
, (3.26)
α= cosЕE
пад||пад
.
Аналогичные соотношения можно записать для отраженной и
прошедшей волны. Необходимо помнить, что угол наклона в
них будет другим: и .
отр
α
прош
α
Если луч попадает из среды, оптически более плотной, в
среду, оптически менее плотную ( ), то возможно полное
отражение луча (полное внутреннее отражение). При этом луч
не проходит во вторую среду, и угол преломления в 3.1 равен
нулю 0
21
nn >
=
ψ
. Отсюда можно найти предельный угол падения
луча, соответствующий полному внутреннему отражению
1
2
кр
n
n
sin =ϕ
. (3.27)
При полном отражении модуль коэффициента отражения по ам-
плитуде равен единице, но меняется фаза волны:
||
i
||пад||отр
eЕE
δ
=
, (3.28)
31
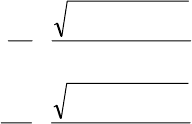
⊥
δ
⊥⊥
=
i
падотр
eЕE,
где и - сдвиг фаз для волны параллельной и перпендику-
лярной поляризации соответственно при полном внутреннем
отражении. При этом
||
δ
⊥
δ
ϕ
−ϕ
=
δ
cosn
nsin
2
tg
2
21
2
21
2
||
, (3.29)
ϕ
−ϕ
=
δ
⊥
cos
nsin
2
tg
2
21
2
.
Выводы
Формулы Френеля позволяют проводить расчет коэффици-
ентов отражения и прохождения для волн параллельной и пер-
пендикулярной поляризации при распространении света через
границу раздела двух сред.
Вопросы и задачи
3.1. Сформулируйте законы отражения и преломления света.
3.2. Как определяется коэффициент отражения (преломления)
света по амплитуде? О чем говорит отрицательной значе-
ние коэффициента отражения по амплитуде?
3.3. Что такое угол Брюстера? Как его рассчитать?
3.4. В чем заключается явление полного внутреннего отражения
света? При каком соотношении между показателями пре-
ломлений сред наблюдается полное отражение?
3.5. При каком значении угла падения θ луч, отраженный от по-
верхности воды, будет перпендикулярен к преломленному
32
ЛЕКЦИЯ 4
Распространение света в неоднородных средах.
Гауссовы пучки
4.1. Уравнение эйконала
В среде с однородным показателем преломления реше-
ниями уравнений Максвелла являются плоские волны. В случае
неоднородной среды, когда , таких решений в виде
плоских волн не существует. Мы знаем, что однородная плоская
волна, распространяющаяся в среде с показателем преломления
n в направлении, описываемом волновым вектором
k, описыва-
ется следующими выражениями:
(
zyxnn ,,=
)
rκ
ErЕ
i
0
e)(
−
⋅= , (4.1)
rκ
HrH
i
0
e)(
−
⋅= , (4.2)
где
r - радиус-вектор рассматриваемой точки. Запишем волно-
вой вектор в следующей форме:
sk nk
0
= , (4.3)
где c/k
0
ω
= , с-скорость света в вакууме, s - единичный век-
тор, сонаправленный с волновым вектором
k. Тогда плоские
волны (4.1-4.2) будут выглядеть так:
),(nki
0
0
e)(
rs
ErЕ
−
⋅= , (4.4)
),(nki
0
0
e)(
rs
HrH
−
⋅= . (4.5)
В случае неоднородной среды разумно предположить, что
электромагнитное поле можно приближенно описать при помо-
щи "локально" плоских волн (то есть их можно приближенно
считать плоскими в окрестностях данной точки):
)(Ski
0
0
e)()(
r
rErЕ
−
⋅= , (4.6)
, (4.7)
)(Ski
0
0
e)()(
r
rHrH
−
⋅=
где и )-медленно меняющиеся амплитуды, завися-
щие от координат,
)(
0
rE (
0
rH
S(
r) - некоторая вещественная скалярная функция положения.
Функция S(
r) называется эйконалом.
33

Волновая поверхность - геометрическое место точек, ко-
леблющихся в одинаковой фазе. С использованием понятия эй-
конал, волновая поверхность - это совокупность точек, удовле-
творяющих условию:
const)(S =r . (4.8)
Представление (4.6-4.7) в виде "локально" плоских волн
справедливо лишь при выполнении условия медленности изме-
нения амплитуд поля:
λ
Δ
<<
Δ x
E
E
, (4.9)
λ
Δ
<<
Δ x
H
H
. (4.10)
Это означает, что когда относительное изменение амплитуды
напряженностей поля должны быть малы по сравнению с разме-
рами системы Δ , выраженными в длинах волн . x λ
Таким образом, на каждом малом участке волну можно рас-
сматривать как плоскую, то есть волновую поверхность можно
заменить частью плоскости, касательной к ней в рассматривае-
мой точке. В результате мы приходим к концепции световых
лучей, направленных по нормали к волновой поверхности, то
есть к геометрической оптике.
Если разложения (4.6-4.7) подставить в уравнения Максвел-
ла для случая отсутствия сторонних токов и зарядов, получим
так называемое
уравнение эйконала:
() ()
rr
2
2
nSgrad = , (4.11)
или
()
zyxn
z
s
y
s
x
s
,,
2
2
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
.
Величина S(r) определяет световой луч в каждой точке волно-
вой поверхности. Следовательно, уравнение эйконала является
основным уравнением геометрической оптики.
4.2. Распространение лазерных пучков
Следующие несколько лекций посвящены проблемам рас-
пространения лазерных пучков в различных средах, так как ла-
зеры широко применяются для передачи сигналов по оптоволо-
34
конным линиям связи. Лазерный пучок, в отличие от бесконеч-
ных плоских волн, ограничен в поперечном направлении и уши-
ряется по мере распространения. Лазерный пучок представляет
собой когерентное электромагнитное излучение, и его распро-
странение описывается уравнениями Максвелла. Лазерный пу-
чок имеет высокую степень монохроматичности, поэтому есте-
ственно по-прежнему предположить следующую временную
зависимость:
ti
e
ω
=
m
EE
&&
, (4.12)
ti
e
ω
=
m
HH
&&
.
По-прежнему, рассматриваем волны как решения уравнений
Максвелла (2.4):
⎪
⎩
⎪
⎨
⎧
=+∇
=+∇
. 0
, 0
22
22
mm
mm
HkH
EkE
&&
&&
4.3. Гауссовы пучки в однородной среде
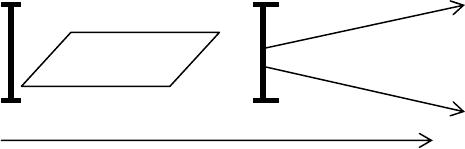
(1)
Активная
среда
Выходной пучок
(
2
)
Oz
Рис. 4.1
Рассмотрим лазер и генерируемый им пучок излучения (см.
рис. 4.1). Цифрами (1) и (2) на рисунке обозначены плоскопа-
раллельные зеркала, (1) - непрозрачное, (2) - полупрозрачное
зеркало. Зеркала (1) и (2) составляют лазерный резонатор или
резонатор Фабри-Перо. Излучение, возникающее в активной
среде, испытывает многократное отражение от зеркал. При каж-
дом отражении от зеркала происходит дифракция. После много-
кратного отражения лазерное излучение выходит наружу через
35
зеркало (2), имея в результате дифракции гауссово распределе-
ние амплитуды и уширение вдоль оси Oz.
Гауссовым пучком называется пучок, поперечное распре-
деление напряженности электрического поля в котором опреде-
ляется функцией Гаусса:
)
2
r
exp(E)y,x(E
2
0
2
0
ω
−=
, (4.13)
где - амплитуда напряженности электрического поля на оси
пучка,
0
E
22
yxr += -есть расстояние от оси пучка в плоско-
сти, перпендикулярной оси Oz, ω
0
- радиус пучка в перетяжке.
e
E
0
E
0
ω
0
E
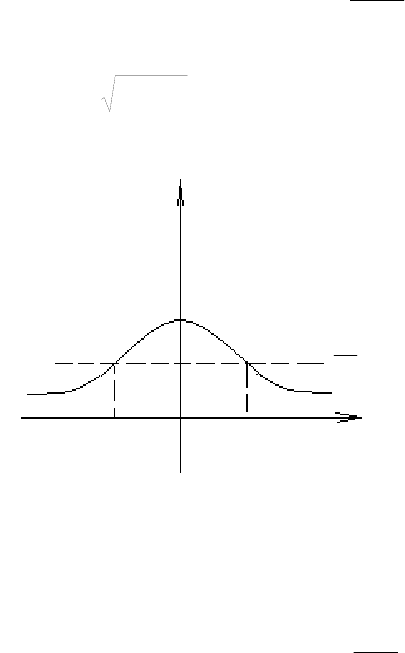
x
0
Рис. 4.2. Распределе-
ние напряженности в
гауссовом пучке в
плоскости y=0 в зави-
симости от координа-
ты x=r. Радиусом
пучка
0
ω
является
такое расстояние от
оси. На котором ам-
плитуда убывает в е
раз по сравнению со
своим значением на
оси.
Интенсивность пучка пропорциональна квадрату ам-
плитуды и описывается соответственно также
функцией Гаусса:
2
)y,x(E~I
)
r
exp(I)y,x(I
2
0
2
0
ω
−=
, (4.14)
где I
o
- интенсивность на оси пучка.
Перетяжка - самое узкое место пучка (см. рис. 4.3).
36
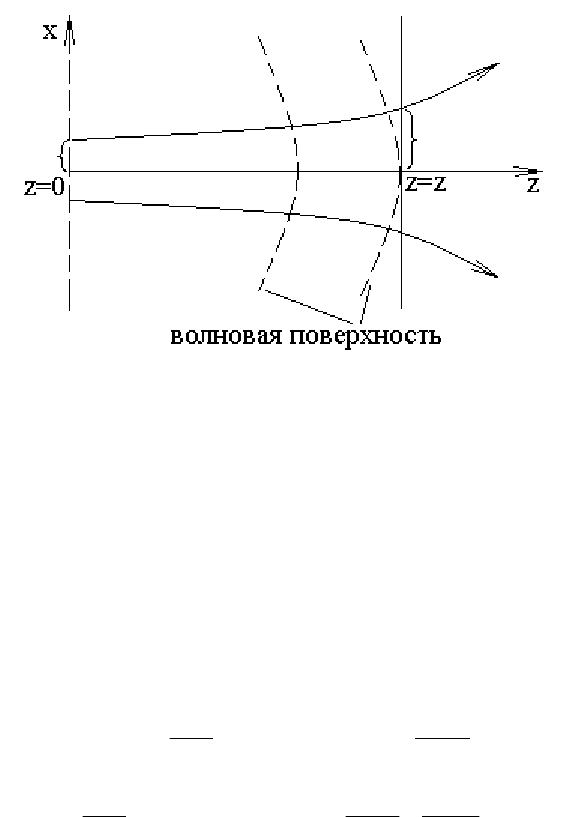
ω
0
ω(z)
Рис. 4.3. Ход лучей в гауссовом пучке в однородной среде.
Здесь z=0 - плоскость перетяжки, пунктиром изображены вол-
новые поверхности.
Гауссов пучок в однородной среде является решением вол-
нового уравнения:
0
22
=+∇
mm
EkE
&&
. (4.15)
При этом предполагается, что вдоль оси Oz фаза меняется ли-
нейно Решение уравнения (4.15) для гауссовых
пучков в среде с цилиндрической симметрией получили Ко-
гельник и Ли:
).ikzexp(~ −
[]
[]
()
()
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
ω
−η−−
ω
ω
=
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−η−−⋅
ω
ω
=
zR2
ik
z
1
r)z(kziexp
)z(
E
)z(q2
kr
i)z(kziexp
)z(
E)z,y,x(E
2
2
0
0
2
0
0
. (4.16)
Здесь q(z) - некоторый комплексный параметр;
ω(z) - ширина распределения интенсивности или радиус пучка
(см. рис. 4.3) :
37

⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+ω=ω
2
0
2
2
0
2
z
z
1)z(
, (4.17)
λ
πω
=
n
z
2
0
0
,
λ - длина волны, z - расстояние от перетяжки;
R(z) - радиус кривизны волновой поверхности (см. рис. 4.3). По
мере распространения вдоль оси Oz радиус кривизны R(z) ме-
няется по закону:
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
2
2
0
z
z
1zzR
. (4.18)
На больших расстояниях от начала координат R совпадает с
расстоянием от перетяжки до волнового фронта z. Это означает,
что в дальней зоне волновой фронт гауссова пучка приближает-
ся к волновому фронту сферической волны, распространяющей-
ся из точки, расположенной на оси пучка в месте его фокальной
перетяжки.
Гауссов пучок — это практичеcки сферическая волна,
идущая из центра и обладающая гауссовым распределением ин-
тенсивности в плоскости, перпендикулярной к направлению
распространения.
В фокальной перетяжке волна является плоской, но про-
странственно ограниченной эффективным размером ω
0
. На
большом расстоянии от перетяжки (z>>π /λ) радиус пучка
вычисляется по формуле:
2
0
ω
0
/z
ω
π
λ
=
ω
. (4.19)
Рассмотрим картину распространения гауссова пучка
(рис.4.4). Траектории лучей задаются гиперболами. На
больших расстояниях z от перетяжки гиперболические по-
верхности , задающие траекторию лучей и на-
правление распространения энергии, асимптотически стре-
222
yx ω=+
38
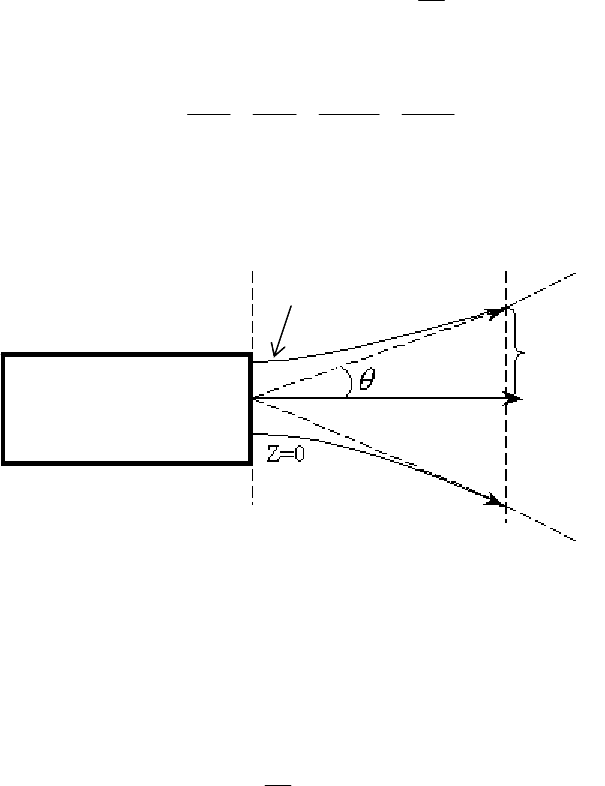
мятся к коническим поверхностям. Половина угла при вер-
шине такого конуса называется угловой расходимостью
пучка:
z/
ω
=θ
.
(4.20)
При больших z из формулы (4.17):
0
0
z
z
)z( ⋅ω=ω
. Тогда угло-
вая расходимость пучка вычисляется по формуле:
n
n
zz
z
z
)z(
0
2
0
0
0
0
πω
λ
=
ωπ
λ
⋅
ω
=
ω
=
ω
=θ , (4.21)
где λ - длина волны, n - показатель преломления среды.
гипе
р
бола
Z
0
ω
ω
(z)
Лазер
плоскость перетяжки
Рис. 4.4. Угловая расходимость θ гауссова пучка.
Угловая расходимость зависит от длины волны и диаметра пуч-
ка в перетяжке. Выясним физический смысл параметра .
Пусть координата вдоль оси Oz равна . Тогда из формулы
(4.17) следует, что
0
z
0
z
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+ω=ω
2
0
2
0
2
0
2
z
z
1)z(
; ,
2
0
2
2)z( ω=ω
39

0
2)z( ω=ω . (4.22)
Значит, - это такое расстояние от перетяжки, на котором ра-
диус пучка увеличивается в
0
z
2 раз.
Выводы
Уравнение эйконала является основным уравнением геомет-
рической оптики. Оно позволяет решить задачу распростране-
ния световых волн в неоднородной среде в случае, когда отно-
сительное изменение амплитуды напряженностей поля должны
быть малы по сравнению с размерами системы , выражен-
ными в длинах волн
xΔ
λ
.
Гауссовы пучки формируются в лазерных резонаторах (в ча-
стности, в резонаторе полупроводникового лазера) в результате
многократного отражения излучения от зеркал. Распределение
интенсивности излучения внутри пучка описывается функцией
Гаусса.
Вопросы и задачи
4.1. При каком условии можно описать поведение волн в неод-
нородной среде через эконал? Из какого уравнения опре-
деляется эйконал?
4.2. Что такое гауссов пучок? Где формируется гауссов пучок?
4.3. Что такое перетяжка гауссова пучка?
4.4. Как определяется угловая расходимость гауссова пучка?
4.5. Найдите радиус кривизны волновой поверхности в перетяж-
ке гауссова пучка.
4.6. Найти угловую расходимость гауссова пучка в кварцевом
стекле, если диаметр пучка в перетяжке равен 10 мкм.
( ,
46,1n = нм1550=
λ
)
40
