George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

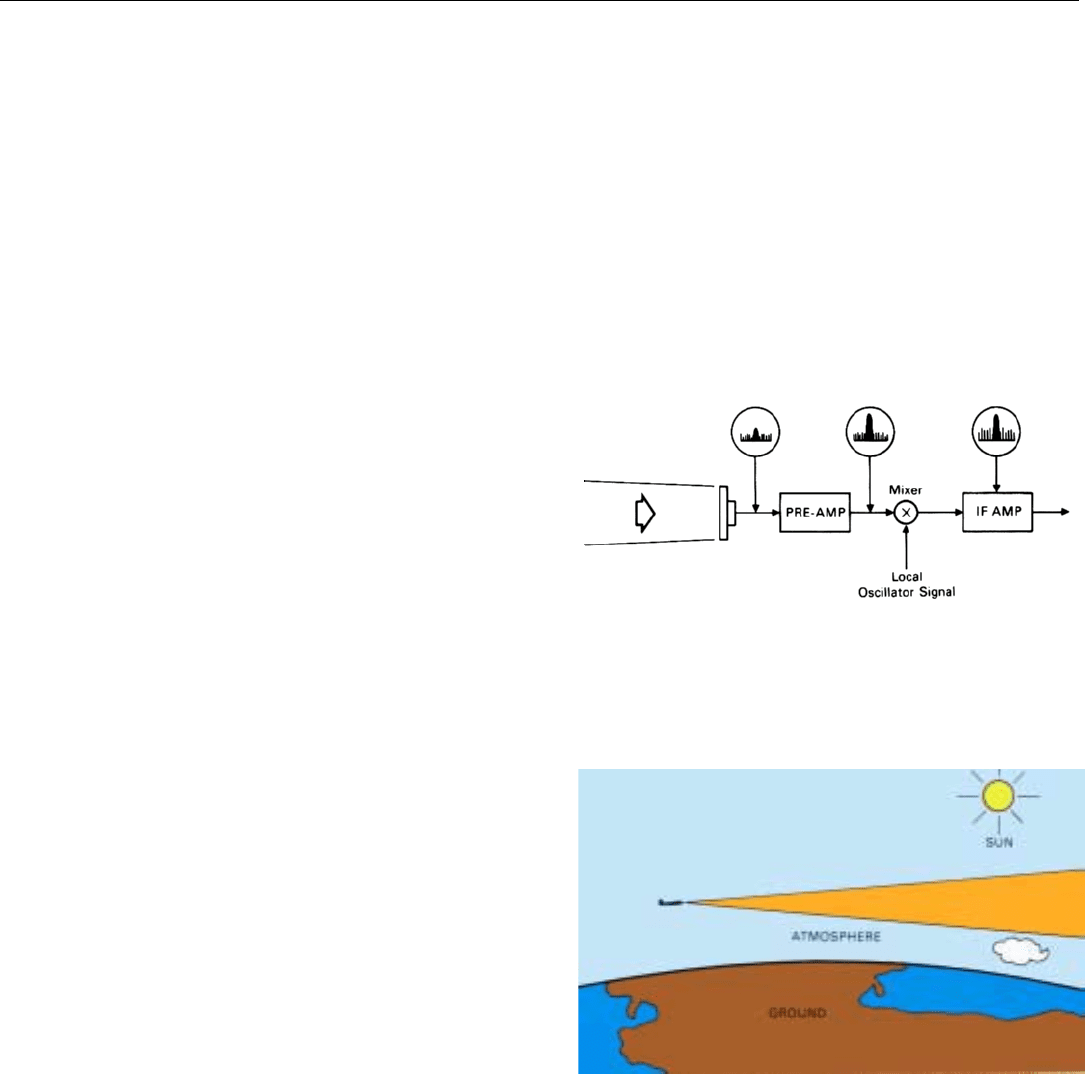
When the internally generated noise is considerably

greater than the external noise (as it is in the vast majority

of airborne radars in operation today), the noise figure, F

multiplied by the foregoing expression for mean noise

power per unit of gain for an ideal receiver is commonly

used to represent the level of background noise against

which target echoes must be detected.

Mean noise power = F

B watts

(Actual receiver)

This expression, it should be remembered, includes both a

nominal estimate of the external noise (equivalent of the

noise generated in a resistor at room temperature) and the

accurately measured internally generated noise.

Although in many receivers, the internal noise predomi-

nates, it can be substantially reduced by adding a low-noise

preamplifier ahead of the receiver’s mixer stage and using a

low-noise mixer (Fig. 7). The preamplifier increases the sig-

nal strength relative to the thermal noise originating in the

subsequent stages, while contributing only a minimum

amount of noise itself. When a low-noise front end is used,

a more accurate estimate may have to be made of the noise

received from sources ahead of the receiver.

Noise from Sources Ahead of the Receiver. As explained

in Chap. 4, because of thermal agitation virtually every-

thing around us radiates radio waves. The radiation is

extremely weak. Nonetheless, it may be detected by a sensi-

tive receiver and add to the noise in the receiver output. At

the frequencies used by most airborne radars, the principal

sources of this natural radiation are the ground, the atmos-

phere, and the sun (Fig. 8).

Radiation from the ground depends not only upon the

temperature of the ground but on its “lossiness,” or absorp-

tion. (The power of the radiated noise is proportional to the

absolute temperature times the coefficient of absorption.)

Thus, although a body of water may have the same temper-

ature as a land mass, since water is a good conductor and

the land usually is not, the water will radiate comparatively

little noise. How much of the radiation that is received by

the radar varies widely with the gain of the antenna and the

direction in which it is looking. For example, far more

noise is received when looking down at the warm earth

than when looking off at a body of water which reflects the

extreme cold of outer space.

The amount of noise received from the atmosphere

depends not only upon the temperature and lossiness of

the atmosphere but upon the amount of atmosphere the

CHAPTER 10 Detection Range

119

7. Receiver noise may be reduced substantially by providing a

low-noise preamplifier ahead of the mixer and/or using a

low-noise mixer.

8. Principal sources of noise outside the aircraft. Amount

received varies with antenna gain and direction.

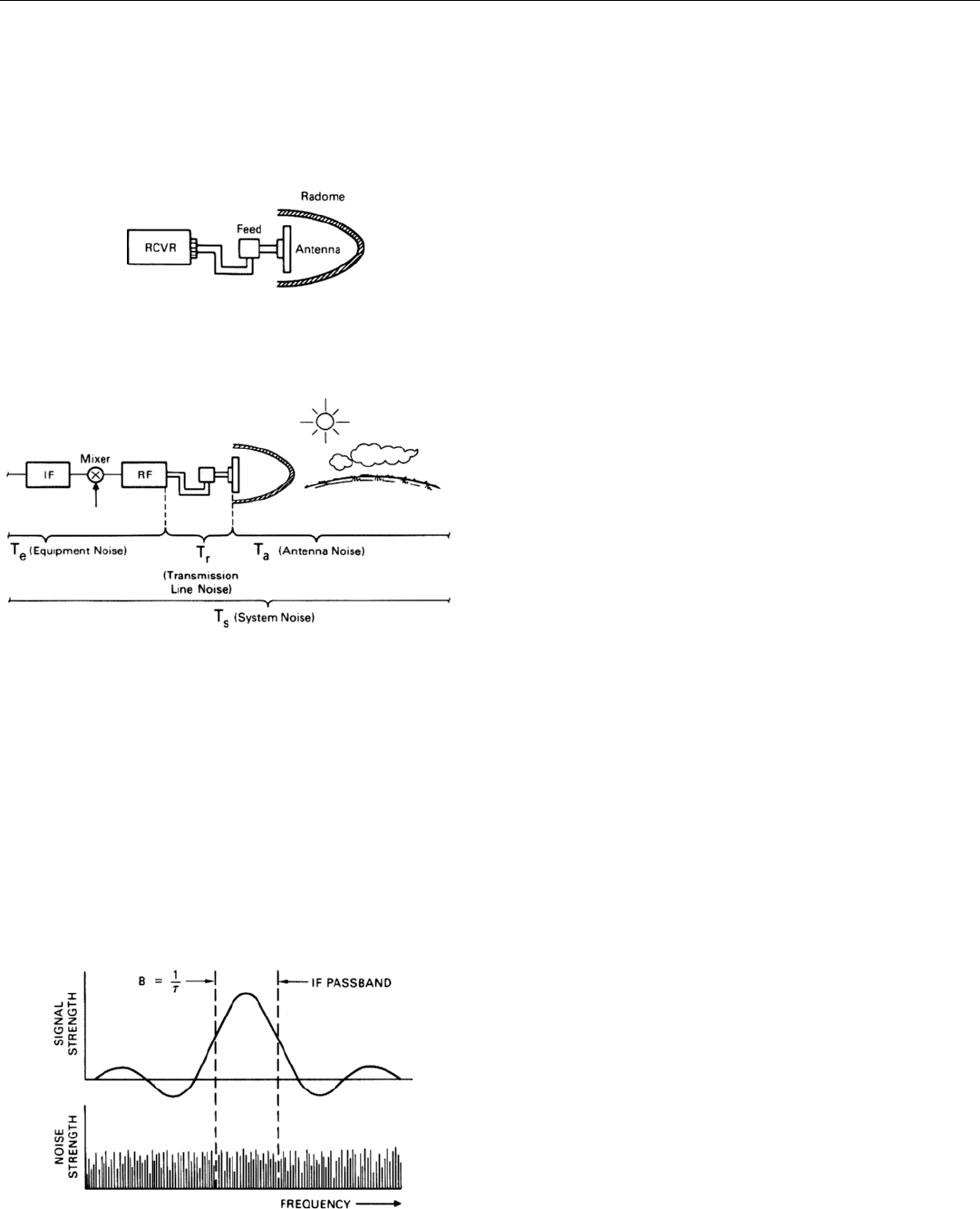
PART III Radar Fundamentals

120

antenna is looking through. Since the lossiness varies with

frequency, the received noise also depends upon the radar’s

operating frequency.

Noise received from the sun varies widely with both

solar conditions and the radar’s operating frequency.

Naturally, it is vastly greater if the sun happens to be in the

antenna’s mainlobe, as opposed to its sidelobes.

Within the aircraft carrying the radar, noise is radiated

by the radome, the antenna, and the complex of wave-

guides connecting the antenna to the receiver (Fig. 9).

Noise from these sources is likewise proportional to their

absolute temperature times their loss coefficients.

As previously noted, noise from all of these external

sources which falls within the receiver passband has essen-

tially the same spectral characteristics as receiver noise.

Consequently, when external noise is significant, the noise

from each source, as well as the receiver noise, is usually

assigned an equivalent noise temperature (Fig. 10). These

temperatures are combined to produce an equivalent noise

temperature for the entire system, T

. The expression for

noise power then becomes

Mean noise power = kT

(All sources)

Competing Noise Energy. Whether noise is expressed in

terms of receiver noise figure, F

, or equivalent noise

temperature, T

, it is noise energy, not power, with which a

target’s echoes must compete. As explained in the last chap-

ter, power is but the rate of flow of energy. Noise energy is

noise power times the length of time over which the noise

energy flows—in this case, the duration of the period in

which return may be received from any one resolvable

increment of range. Therefore,

Mean noise energy = kT

where t

is the duration of the noise.

For any given noise temperature and duration, the noise

can be reduced by minimizing the receiver bandwidth, B. A

common practice is to narrow the IF passband until it is

just wide enough to pass most of the energy contained in

the received echoes. This is called a matched filter design

(Fig. 11).

Another way of looking at this is that the tuned circuits

of the receiver IF amplifier integrate the received energy

during the width, τ, of each received pulse. They thus

9. Other sources of noise within the aircraft.

10. When external noise is significant, noise from each source is

assigned an equivalent noise temperature.

11. Signal-to-noise ratio may be maximized by narrowing the

passband of the IF amplifier to the point where only the bulk of

the signal energy is passed.

1. Since T

does not include the

noise of the input resistance,

as F

does, T

= T

– 1).

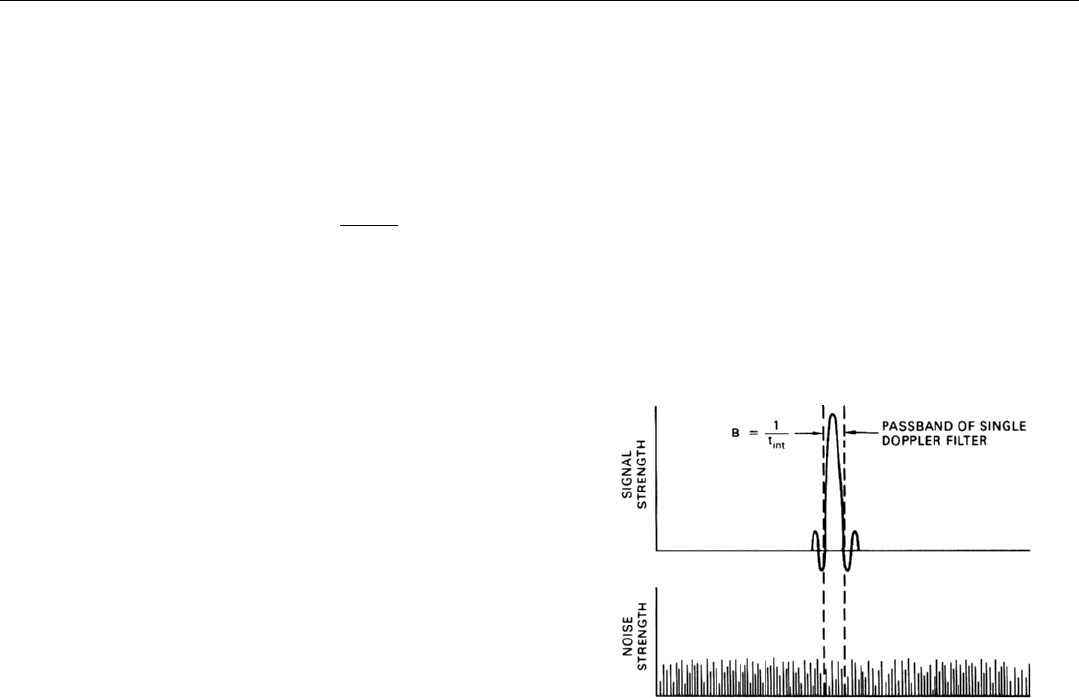
accumulate the energy the pulse contains and reject the

noise outside the pulse’s bandwidth. The optimum band-

width turns out to be very nearly equal to one divided by

the pulse width, τ. When 1/τ is substituted for B in the

expression for mean noise, it becomes

Mean noise energy =

(Matched filter design)

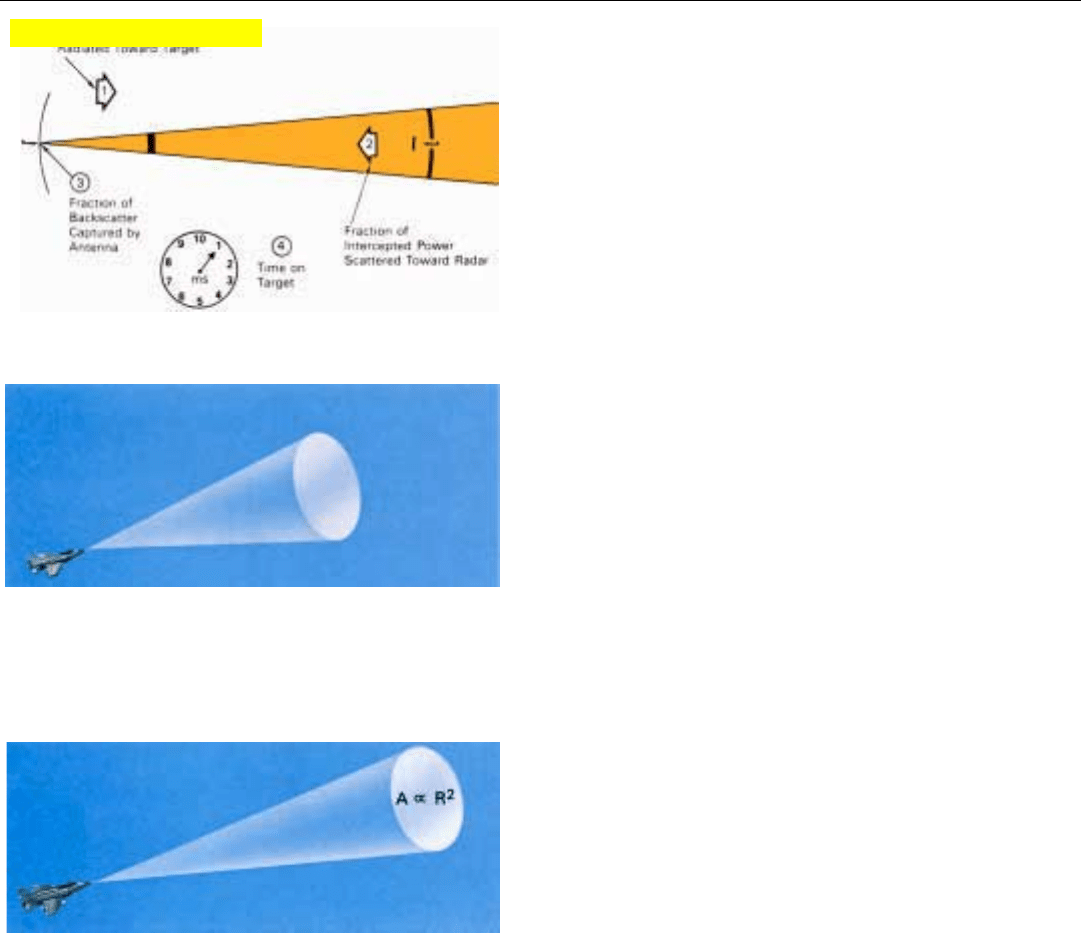
In doppler radars, bandwidth is further reduced by

doppler filters, which follow the IF amplifier. (A separate

filter is generally provided for every anticipated combina-

tion of resolvable range and doppler frequency.) As will be

explained in Chap. 18, the passband of a doppler filter is

approximately equal to 1/t

int

, where t

int

is the time over

which the filter adds up (integrates) the radar returns

(Fig. 12).

Whereas τ is on the order of microseconds, t

int

is on the

order of milliseconds. Consequently, the passband of a

doppler filter is on the order of 1/1000th of the width of

the IF passband.

The integration time, t

int

, is also the length of time over

which the noise is received and integrated by the filter.

When t

int

is substituted for t

and 1/t

int

is substituted for

1/ τ, the two terms cancel, leaving

Mean noise energy = kT

(Doppler radar)

One way of looking at the effect of a doppler filter on the

noise is this. As the noise energy flows into the filter, the fil-

ter’s passband (which is inversely proportional to integra-

tion time) simultaneously narrows. As a result, the level of

the noise energy that accumulates in the filter is more or

less independent of the length of the integration period.

Noise being random, of course, the level of the accumu-

lated energy may vary widely from one integration period

to another. But its mean value over a great many integration

periods will be kT

On average, therefore, for a target to be detected, enough

energy must be received from it to noticeably raise the filter

output above this mean level.

And that brings us to the question: what determines how

much energy is received from a target; what is the energy of

the signal?

CHAPTER 10 Detection Range

121

12. In a doppler radar the passband is further narrowed by

doppler filtering.

PART III Radar Fundamentals

122

Energy of the Target Signal

Four basic factors (Fig. 13) determine the amount of

energy a radar will receive from a target during any one

period of time that the antenna beam is trained on it:

• Average power—rate of flow of energy—of the radio

waves radiated in the target’s direction

• Fraction of the wave’s power which is intercepted by

the target and scattered back in the radar’s direction

• Fraction of that power which is captured by the radar

antenna

•

Length of time the antenna beam is trained on the target

When the antenna is trained on a target, the power den-

sity of the radio waves radiated in the target’s direction is

proportional to the transmitter’s average power output, P

avg

times the gain, G, of the antenna’s mainlobe (Fig. 14).

(Power density, you will recall, is the rate of flow of energy

per unit of area normal to the wave’s direction of propaga-

tion.)

In transit to the target, the power density is diminished

as a result of two things: absorption in the atmosphere, and

spreading. Except at the shorter wavelength, attenuation

due to absorption is comparatively small. For the moment it

will be neglected, but not the reduction in power density

due to spreading.

As the waves propagate toward the target, their energy

spreads—like the substance of an expanding soap bubble—

over an increasingly large area (Fig. 15). This area is propor-

tional to the square of the distance from the radar. At the

target’s range, say R miles, the power density is only 1/R

times what it was at a range of 1 mile.

The amount of power intercepted by the target equals the

power density at the target’s range times the geometric

cross-sectional area of the target, as viewed from the radar

(the projected area).

What fraction of the intercepted power is scattered back

toward the radar depends upon the target’s reflectivity and

directivity. The reflectivity is simply the ratio of total scat-

tered power to total intercepted power. The directivity—like

the gain of an antenna—is the ratio of the power scattered

in the direction of the radar to the power which would have

been scattered in that direction had the scattering been uni-

form in all directions.

Customarily, a target’s geometric cross-sectional area,

reflectivity, and directivity are lumped into a single factor,

called radar cross section. It is represented by the Greek letter

sigma, σ, and is usually expressed in square meters. (See

panel on right.)

14. Density of power radiated in target’s direction is proportional

to the average radiated power times the antenna gain in that

direction.

15. As waves travel out to a target, their power is spread over an

increasingly large area.

2. Another term for power

density is “power flux.”

13. Factors which determine energy of target signal.

Power Density ∝ P

avg

Click for high-quality image

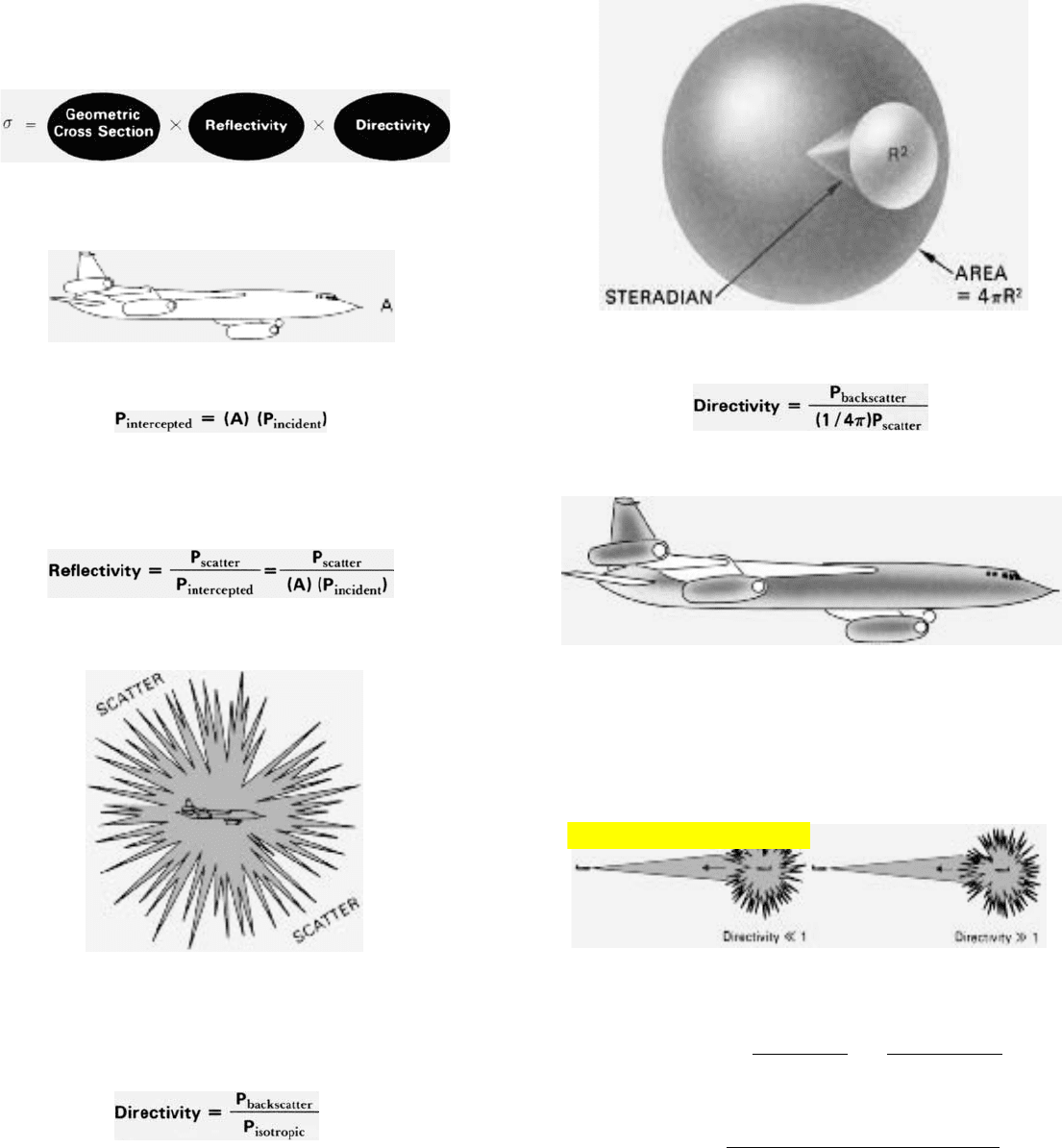
Since the area of a sphere is 4π times the radius squared, a

sphere contains 4π steradians. Therefore:

A target may be thought of as consisting of a great many indi-

vidual reflecting elements (scatterers).

The extent to which the scatter from these combines construc-

tively in the direction of the radar depends upon the relative

phases of the backscatter from the individual elements. That in

turn depends on the relative distances (in wavelengths) of the

elements from the radar. Depending on the configuration and

orientation of the target, the directivity may range anywhere

from a small fraction to a large number.

Complete Expression for

. Expanded in terms of the factors

outlined in the preceding paragraphs, the basic expression for

radar cross section becomes:

Cancelling like terms and spelling out those that remain yields:

This is the common form of the definition of radar cross section.

It has the advantage of making radar equations easier to write.

But expressing

in terms of geometric cross section, reflectivity,

and directivity is more illuminating since that shows the

relationship between

and the factors that determine its value.

CHAPTER 10 Detection Range

123

A ×

scatter

backscatter

(A) (

incident

) (1 / 4π) (

scatter

)

4π

Backscatter per steradian

Power density of intercepted waves

RADAR CROSS SECTION

A target’s radar cross section,

, is most easily visualized as

the product of three factors:

Geometric Cross Section is the cross-sectional area of the

larget as viewed from the radar.

This area determines how much power the target will intercept.

where P

incident

is the power density of the incident waves.

Reflectivity is the term for the fraction of the intercepted

power that is reradiated (scattered) by the target.

(The scattered power equals the intercepted power less

whatever power is absorbed by the target.)

Directivity is the ratio of the power scattered back in the

radar’s direction to the power that would have been

backscattered had the scattering been uniform in all directions,

i.e., isotropically.

Normally, P

backscatter

and P

isotropic

are expressed as power per

unit of solid angle. P

isotropic

then equals P

scatter

divided by the

number of units of solid angle in a sphere.

The unit of solid angle is the steradian. It is the angle

subtended by an area on the surface of a sphere equal to the

radius squared.

Click for high-quality image

PART III Radar Fundamentals

124

16. Density of power reflected in radar’s direction equals density

of intercepted wave times radar cross section.

17. Reflected power undergoes equal amount of spreading in

returning to radar.

The power density of the waves scattered back in the

radar’s direction, then, can be found by multiplying the

power density of the transmitted waves when they reach

the target by the target’s radar cross section (Fig. 16). Since

the directivity of a target can be quite high, for some target

aspects the radar cross section may be many times the geo-

metric cross-sectional area. For others, the reverse may be

true.

As the waves propagate back from the target, they under-

go the same geometrical spreading as on their way out.

Their power density, which has already been reduced by a

factor of 1/R

is again reduced by 1/R

(Fig. 17). The two

factors are compounded, so the power density when the

waves reach the radar is only 1/R

x 1/R

= 1/R

times what

it would be if the target were at a range of only 1 mile (or

whatever other unit of distance R is measure in).

To give you a feel for the magnitude of this difference,

the relative strengths of the echoes from the same target in

the same aspect at ranges of 1 to 50 miles are plotted

below (Fig. 18). For a range of 1 mile, the strength is arbi-

trarily assumed to equal 1. At 50 miles, the relative

strength is only 0.00000016—too small to be discernible

in the figure.

18. Reduction in strength of target echoes with range. Echoes from tar-

get at 50 miles are only 0.00000016 times as strong as echoes

from same target at 1 mile range.

19. Reflected power intercepted by radar is proportional to effec-

tive area of antenna.

Incidentally, Fig. 18 dramatically illustrates why the

receiver must be able to handle powers of vastly different

magnitudes—i.e., have a wide dynamic range.

When the backscattered waves reach the antenna, it

intercepts a fraction of their power. That fraction equals the

power density of the waves times the effective area of the

antenna, A

(Fig. 19). The total amount of energy intercept-

ed equals that product times the length of time the antenna

is trained on the target, t

As we saw in Chap. 8, the area A

takes into account the

aperture efficiency of the antenna. For all of the intercepted

energy to be constructively added up by the antenna feed,

of course, the target must be centered in the antenna’s

mainlobe.

If we multiply together the several factors which we have

identified as governing the amount of energy received from

a target, we get the following expression for received target

signal energy.

Signal energy ≅ K

avg

GσA

where

K = factor of proportionality (1/4π)

avg

= average transmitted power

G = antenna gain

σ = radar cross section of the target

= effective area of the antenna

= time-on-target

R = range

This expression roughly indicates the total amount of

energy that would be received by a radar during the antenna

beam’s time-on-target, t

. Whether all of the energy is actu-

ally utilized depends upon the radar’s ability to integrate it.

In simple non-doppler radars, integration is performed

by the display (e.g., by the phosphor that causes the image

to persist on the face of the CRT) and by the eyes and the

mind of the operator (Fig. 20). Because it takes place after

detection, this integration is called postdetection integration.

In a doppler radar, integration is performed primarily by

the signal processor’s doppler filters before detection takes

place. Provided the integration time, t

int

, is made equal to

the above expression indicates the amplitude of the

integrated target signal in the output of a filter at the end of

each time-on-target. Whether the target will be detected, of

course, depends upon the ratio of this amplitude to that of

the integrated noise, discussed earlier.

To fully understand the relationship between signal-to-

noise ratio and maximum detection range, though, we must

know a little more about the actual detection process.

Detection Process

A small target, we will assume, is approaching a search-

ing doppler radar from a very great distance. Initially, the

target echoes are extremely weak—so weak they are com-

pletely lost in the background noise.

On first thought, one might suppose the echoes could be

pulled out of the noise by increasing the gain of the receiv-

er. But the receiver amplifies noise and echoes equally.

Increasing its gain in no way alters the situation.

CHAPTER 10 Detection Range

125

20. In non-doppler radars, integration takes place on the display

and in the eyes and mind of the operator.

3. And provided the target is

centered in the passband of

one of the filters and the time

on target coincides exactly

with an integration period.

If you're puzzled, the value of 4π

for K in the equation

for received signal energy, may be explained as follows:

Density of power

reaching target

= P

avg

Area of a sphere

of radius R

Density of power

returned to radar

= P

reflected

Directivity factor

included in σ

Area of a sphere

of radius R

Area of a sphere

of radius R

= 4

πR

Therefore: Both G and σ must be divided by 4πR

G σ Gσ

4πR

(4π)

THE SCALE FACTOR K

Hence:

K =

(4π)

PART III Radar Fundamentals

126

Each time the antenna beam sweeps over the target, a

stream of pulses is received (Fig. 21). A doppler filter in the

radar’s signal processor adds up the energy contained in

this stream. The target signal in the output of the filter thus

corresponds fairly closely to the total amount of energy

received during the antenna beam’s time-on-target. This

energy is indistinguishably combined with the noise energy

that has accumulated in the filter during the same period.

As the target’s range decreases, the strength of the inte-

grated signal increases. The mean strength of the noise, on

the other hand, remains about the same. Eventually, the sig-

nal becomes strong enough to be detected above the noise

(Fig. 22).

In doppler radars, detection is performed automatically.

At the end of every integration period, the output of each fil-

ter is applied to a separate detector. If the integrated signal

plus the accompanying noise exceeds a certain threshold,

the detector concludes that a target is present, and a bright,

synthetic target blip is presented on the display. Otherwise,

the display remains perfectly clear (Fig. 23).

23. If the receiver output exceeds the detection threshold, a bright, syn-

thetic blip appears on the display.

24. The higher the threshold is above the mean level of the noise,

the lower the probability of a spike of noise crossing it and

producing a false alarm.

25. Yet, if the threshold is too high, some detectable targets may

go undetected.

21. Each time the antenna beam sweeps across the target, a

stream of echoes is received.

22. Received signal energy, for successive times-on-target. As range

decreases, ratio of signal energy to noise energy increases.

The completely random noise alone will occasionally

exceed the threshold, and the detector will falsely indicate

that a target has been detected (Fig. 24). This is called a

false alarm. The chance of its occurring is called the false-

alarm probability. The higher the detection threshold rela-

tive to the mean level of the noise energy, the lower the

false-alarm probability will be, and vice versa.

Clearly the setting of the threshold is crucial. If it is too

high (Fig. 25), detectable targets may go undetected. If it is

too low, too many false alarms will occur. The optimum set-

ting is just enough higher than the mean level of the noise

to keep the false-alarm probability from exceeding an

acceptable value. The mean level of the noise, as well as the

system gain, may vary over a wide range. Consequently, the

output of the radar’s doppler filters must be continuously

monitored to maintain the optimum threshold setting.

Generally, the threshold for each detector is individually

set on the basis of both the probable noise level in the filter

whose output is being detected (the “local” noise level) and

the average noise level in all of the filters (the “global” noise

level). Typically, the local level is determined by averaging

the outputs of a group (ensemble) of filters on either side of

the one in question. Since most of these outputs will be due

to noise, the average can be assumed to approximate the

probable noise level in the bracketed filter.

The global noise level is determined by establishing a

second, noise-detection threshold for every filter. This

threshold is set far enough below the target-detection

threshold so that in aggregate vastly more threshold cross-

ings are made by noise spikes than by target echoes. By

continually counting these crossings and statistically adjust-

ing the count for the difference between the two thresholds,

the false-alarm rate for the entire system can be determined.

Exactly how the local ensemble of filters is selected and

how the average for the ensemble is weighted in compari-

son to the system false-alarm rate varies from system to sys-

tem and mode to mode. As nearly as possible, however, the

thresholds are set so as to maintain the false-alarm rate for

each detector at the optimum value. If the rate is too high,

the thresholds are raised; if it is too low, the thresholds are

lowered. For this reason, the automatic detectors are called

constant false-alarm-rate (CFAR) detectors.

Regardless of how close to optimum it is, the setting of

the target detection threshold, relative to the mean level of

the noise, establishes the minimum value of integrated sig-

nal energy, s

det

, that, on average, is required for target detec-

tion (Fig. 26). Bear in mind, though, that because of the

randomness of the noise energy about its mean value, the

signal plus the accompanying noise will sometimes exceed

the threshold even when the signal energy is less than s

det

Likewise, at other times it will fail to reach the threshold,

even when the signal energy is greater than s

det

Nevertheless, the range at which a given target’s integrat-

ed signal becomes equal to s

det

can be considered to be the

maximum detection range (under the existing operating

conditions) for that particular target.

Integration and Its Leverage on Detection Range

Although implicit in the expression for signal energy

(page 125), the immense importance of integration in

pulling the weak echoes of distant targets out of noise is

often overlooked. One can gain a valuable insight into this

important process by performing a simple experiment.

Experimental Setup. To see how noise energy and signal

energy integrate in a narrow bandpass (doppler) filter we

set up a rudimentary radar to look for a test target at a

given range and angle. Having trained the antenna in the

CHAPTER 10 Detection Range

127

26. The setting of the threshold relative to the mean noise level

establishes the minimum value of integrated signal, S

det

required for detection.

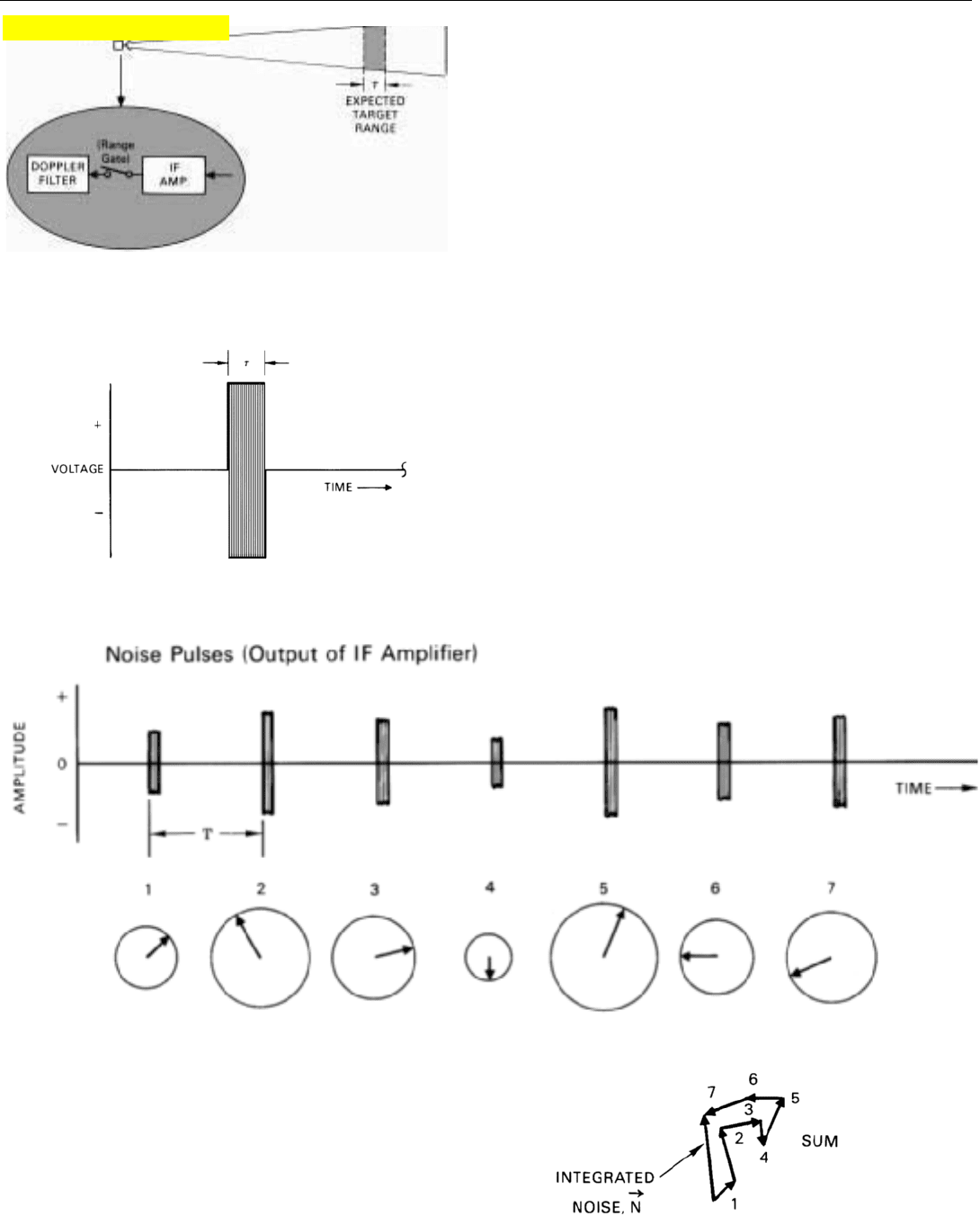
PART III Radar Fundamentals

128

expected target’s direction, we turn on the receiver for a

fixed period of time. Meanwhile, at that point in each inter-

pulse period when return will be received from the expect-

ed target’s range, we momentarily close a switch (range

gate). It passes a slice of the receiver’s IF output—one

pulsewidth wide—to a narrowband filter (Fig. 27). The fil-

ter is tuned to the target’s doppler frequency.

Noise Alone, Single Integration Period. Initially, we per-

form the experiment with no target present. When the

range gate is closed, all the filter receives is a pulse of noise

energy.

In this radar, as in most, the passband of the receiver’s IF

amplifier is just wide enough to pass the bulk of the energy

in a target echo (matched filter design). Consequently, hav-

ing passed through the IF amplifier and been sliced into

narrow pulses, the noise looks much like target return (Fig.

28). The principal difference as seen by the doppler filter is

this. Whereas the phase of the pulses received from a target

is constant from pulse to pulse, the phase as well as the

amplitude of the noise pulses varies randomly from pulse to

pulse. We can see the variation in phase most clearly if we

represent the pulses with phasors (Fig. 29).

29. Phasor representation of noise pulses applied to doppler filter.

Because of phase variation, amplitude of integrated noise is only a fraction of

the sum of amplitudes of the individual pulses.

27. A rudimentary radar is set up to look for a target at a given

range. Switch closes at the point in the interpulse period when

return is received from the expected target’s range.

28. Having passed through the IF amplifier and been sliced very

thin, each noise pulse looks much like target return.

Click for high-quality image