George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

As with antenna size, decreasing λ would also decrease

the beamwidth (θ

3db

∝λ/d). In search, therefore, to keep

the increase in range from being wiped out by a reduction

in t

, the scan would have to be slowed down (Fig. 15).

Because the range equation we have been using doesn’t

account for the effect of changes in wavelength and antenna

size on t

, it is not as illuminating as it might be for situa-

tions where a given volume of target space must be

searched for a given period of time. For volume search,

therefore, a slightly different form of the equation is com-

monly used.

Equation for Volume Search

To tailor the range equation to volume search, the time-

on-target (t

) must be expressed in terms of (1) the length

of time the antenna takes to complete one frame of the

search scan, and (2) the size of the solid angle subtended

by that frame. The scan frame time is represented by t

; the

solid angle, by the product of the azimuth and elevation

angles spanning the frame, θ

and θ

, respectively. While

this conversion is straightforward (see panel, bottom of

next page), we can get a better physical feel for the funda-

mental relationships involved in volume search by starting

from scratch with a simplified derivation.

Simplified Derivation. The total energy radiated during

any one frame time, t

, equals P

avg

. Assuming that the scan

spreads the energy uniformly over the entire solid angle,

the fraction of the energy that is intercepted by a target and

scattered back toward the radar is proportional to the ratio

of (a) the target’s radar cross section to (b) the cross-section-

al area of the solid angle of the search scan at the target’s

range (Fig. 16). The fraction of the backscattered energy

captured by the radar antenna is proportional to A

(Fig. 17).

For volume search, therefore, the simplified range

equation can be rewritten as

∝

avg

where

= frame time

= azimuth angle scanned

= elevation angle scanned

and the other terms are as previously defined.

Ignoring target radar cross section—over which we have

no control—and rearranging, we get

∝

avg

PART III Radar Fundamentals

140

16. During the scan frame time, the total backscattered energy is

proportional to the ratio of the radar cross section (σ) of the

target to the cross-sectional area R

(θ

) of the solid angle

scanned at the target’s range, σ/(R

15. If beamwidth is reduced, scan must be slowed down to pro-

vide the same time-on-target, t

17. Fraction of backscatter intercepted by radar is proportional to

effective antenna area divided by the range squared (A

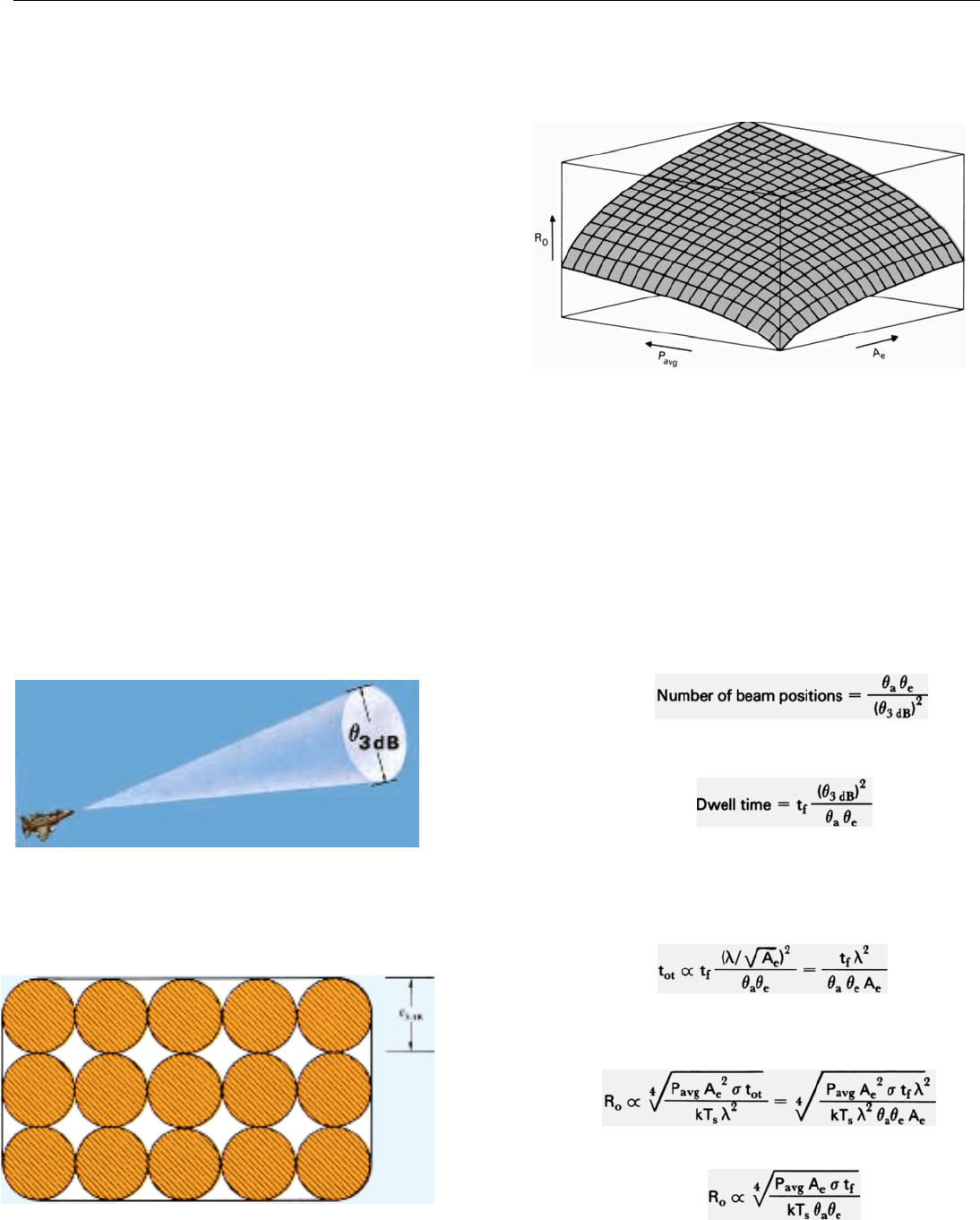
What the Volume Search Equation Tells Us. From this

simple equation, we can draw three important conclusions

regarding detection range in volume search.

• Only through its secondary influences on atmospheric

absorption, available average power, aperture efficien-

cy, ambient noise, target directivity, and so on, does

wavelength affect the range.

• For any combination of frame time and solid angle

searched, range depends primarily upon the product,

avg

(Fig. 18).

• The greater the ratio of the frame time to the size of

the volume searched, the greater the range will be.

Frame time, however, may be limited by required system

reaction time—which is itself a function of detection range.

And the size of the solid angle is dictated by the dispersion

of anticipated targets. Therefore, the equation leads one to

this general conclusion: To maximize detection range for

volume search, use the highest possible average power and

the largest possible antenna.

CHAPTER 11 The Range Equation: What It Does and Doesn’t Tell Us

141

18. For any one combination of frame time and solid angle searched,

detection range can be maximized by using the highest possible

power (P

avg

) and largest possible antenna (A

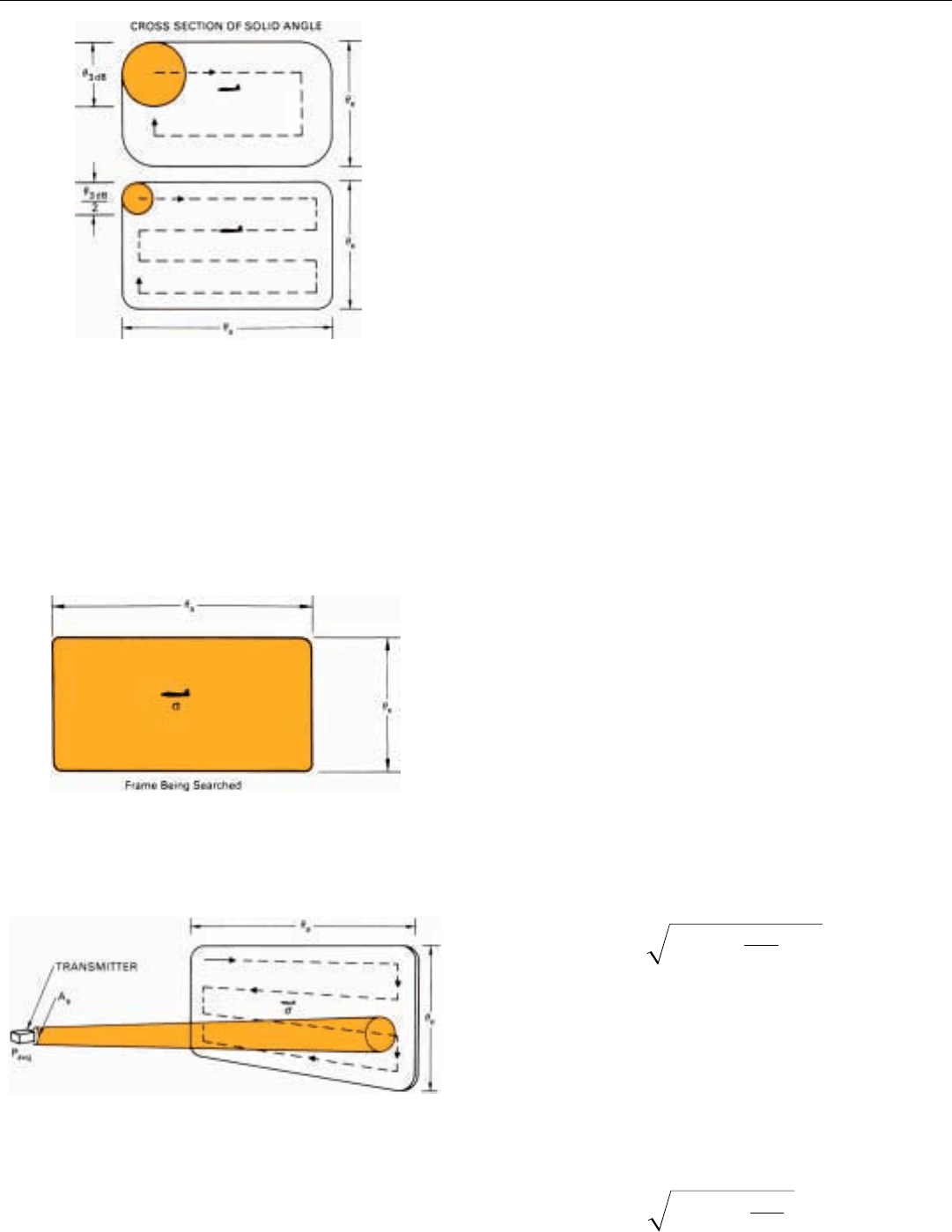
TAILORING THE RANGE EQUATION TO VOLUME SEARCH

In adapting the radar equation to volume search, the antenna

beam is conveniently thought of as having a uniform cross

section of width

3 dB

This beam is then thought of as jumping a beamwidth at a time

through the solid angle that is to be searched.

The number of such positions the beam occupies equals the

cross-sectional area of the solid angle at unity range divided by

the cross section of the beam at the same range.

Since the beam must complete its entire scan in one frame

time (t

), the length of time it dwells on any one target is

Now, the beamwidth is proportional to the ratio of the

wavelength, λ, to the diameter of the antenna, d.

(

3 dB

⬀

λ/d.) And d, in turn, is proportional to the square root of

the effective area of the antenna, 公

. Thus, the dwell time,

Substituting this expression for t

in the range equation given

on page 188, we get:

Cancelling like terms,

20. Polar plot of the radar cross section, σ, of a typical target.

Note how widely σ varies with target aspect.

PART III Radar Fundamentals

142

Even when all pertinent factors have been included in

the radar equation, it cannot tell us with certainty at what

range a given target will be detected. For not only back-

ground noise but radar cross section are continually fluctu-

ating qualities.

Fluctuations in Radar Cross Section

The reason for these fluctuations can be seen if we

think of the target as consisting of a large number of indi-

vidual scatterers (Fig. 19). The extent to which the scatter

from these adds up or cancels in the direction of the

radar depends upon their relative phases. If the phases

are more or less the same, the backscatter will add up to

a large sum. If they are not, the sum may be comparative-

ly small.

The relative phases depend upon the instantaneous dis-

tances in wavelengths of the reflectors from the radar.

Because of the round trip nature of the transmission, a dif-

ference in distance of

/4 wavelength makes a difference in

phase of 180˚.

Since the wavelength may be very short, relatively small

changes in target aspect, even vibration, can cause the tar-

get return to scintillate like the light from a star.

And since

the configuration of many targets is radically different when

viewed from different directions, larger changes in aspect

may produce strong peaks or deep fades (Fig. 20). Over a

period of time these variations will usually average out. But

if the radar-bearing aircraft is approaching on a course that

holds a target in the same relative aspect, a peak or fade

may persist for some time.

During the early days of the all-weather interceptor, in

fact, it was not uncommon to receive complaints from

pilots who had picked up a target in a favorable aspect and

locked onto it at long range, only to lose lock when the

interceptor converted to a constant aspect attack course

that happened to place the target in a deep fade. Being

unfamiliar with the phenomenon, they thought the radar

had malfunctioned.

Since the relative phases of the returns from the individ-

ual elements depend upon wavelength, the target aspects

for which the fades occur will generally be slightly different

for different wavelengths. One way of getting around the

problem of target fading, therefore, is to switch periodically

from one to another of several different radio frequencies,

thereby providing what is called frequency diversity.

Detection Probability

Because of its randomness, detection performance

against targets whose range is limited by thermal back-

3. More precisely, like the light

in a particular spectral line

when a star is at a low eleva-

tion angle.

19. A target may be thought of as myriad, tiny reflectors. How

their echoes add up depends upon their relative phases.

2. Generally, the sums tend to

cluster around a median

value.

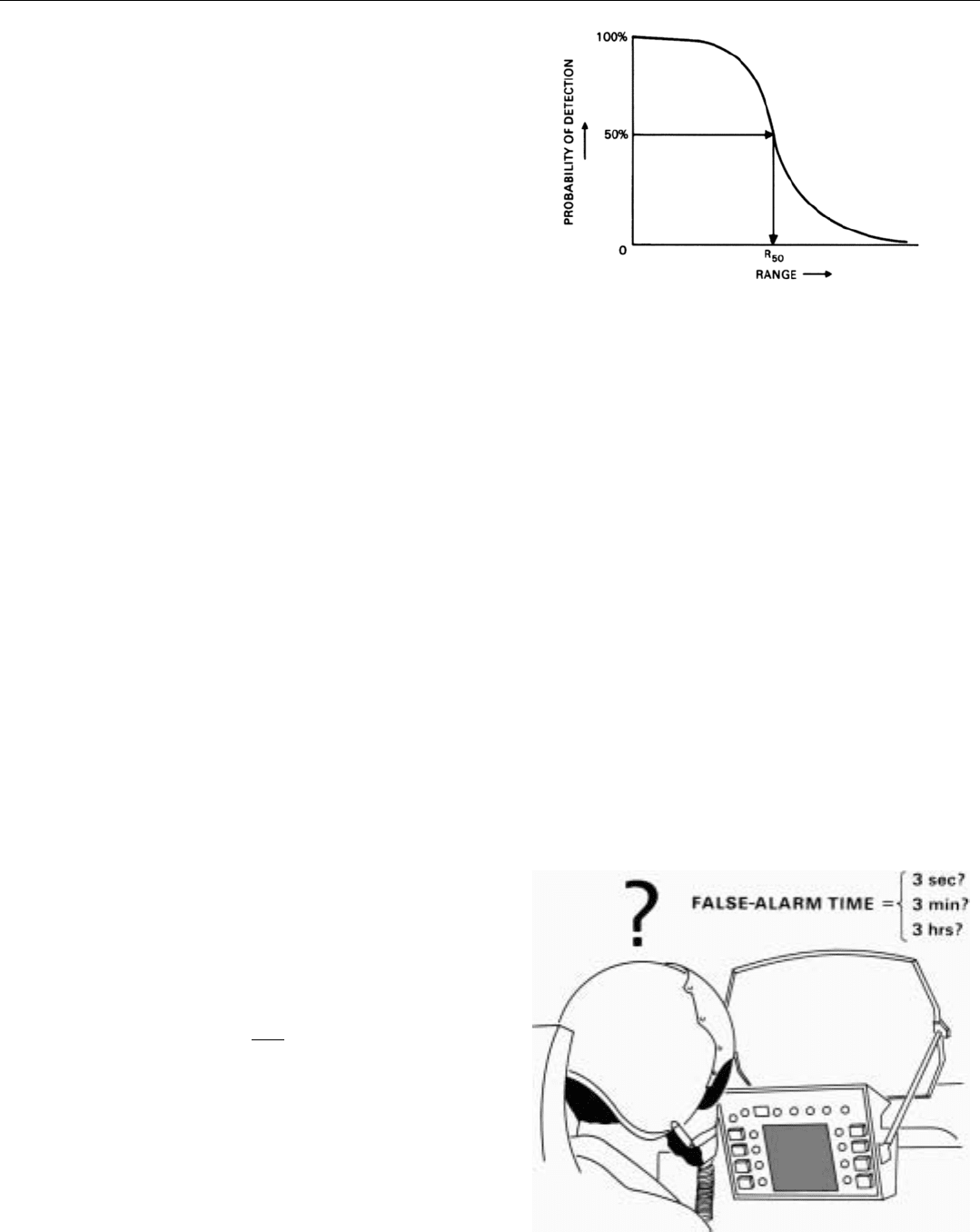
ground noise is usually stated in terms of probabilities. For

search, the most commonly used probability is blip-scan

ratio, P

. It is the probability of detecting a given target at a

given range any time the antenna beam scans across the tar-

get (Fig. 21). It is also referred to as single-scan or single-look

probability. The higher the probability specified, the shorter

the range will be.

The notation used to represent the range is the letter “R”

with a subscript indicating the probability. For instance, R

represents the range for which the probability of detection

is 50 percent; R

, the range for which the probability is 90

percent.

How does one determine the range, say, for a probability

of detection of 60 percent? There are five basic steps:

1. Decide on an acceptable system false-alarm rate.

2. Calculate the corresponding value of the false-alarm

probability for the individual threshold detectors.

3. On the basis of the statistical characteristics of the

noise, find the threshold setting that will limit the

false-alarm probability to this value.

4. Determine the mean value of the integrated signal-to-

noise ratio for which the signal plus the noise will

have the specified probability of crossing the thresh-

old (in this case 60 percent).

5. Compute the range at which this signal-to-noise ratio

will be obtained.

That range is R

What each step actually involves is outlined briefly in the

following paragraphs.

Deciding on an Acceptable False-Alarm Rate. The aver-

age rate at which false alarms appear on the radar display—

i.e., the number of false alarms per unit of time—is called

the false-alarm rate, FAR. The mean time between false

alarms is called the false-alarm time, t

. It, of course, is the

reciprocal of the false-alarm rate.

FAR

If false alarms occur only once every several hours, they

will probably not even be noticed by the radar operator.

Yet, if they occur at intervals on the order of a second, they

may render the radar useless (Fig. 22). What is an accept-

able false-alarm time depends upon the application. Since

raising the detection threshold reduces the maximum

detection range, where long range is desired the false-alarm

time is usually made no longer than necessary to make the

CHAPTER 11 The Range Equation: What It Does and Doesn’t Tell Us

143

21. Blip-scan ratio is probability of detecting a given target at a

given range on any one scan of the antenna.

22. To the radar operator false-alarm probability has little direct

meaning. Time between false alarms does.

23. On average an 8 will be spun once every 38 spins.

(Courtesy Las Vegas News Bureau)

144

radar easy to operate. In radars for fighter aircraft, for

example, a false-alarm time of a minute or so is generally

considered acceptable.

Calculating False-Alarm Probability. The mean time

between false alarms is related to the false-alarm probabil-

ity for the radar’s threshold detectors by the following

equation

int

where

= average time between false alarms for the

system

int

= integration time of the radar’s doppler filters

(plus any PDI)

= false-alarm probability for a single threshold

detector

N = number of threshold detectors

If you’re puzzled, the analogy to the Lucky 8 Casino may

help.

In this casino, whenever a roulette wheel spins an “8,” an

“eight-bell alarm” sounds, all bets at that wheel stay put,

and everyone who has a bet down is served a free glass of

champagne.

Before the casino opened, the question naturally arose:

How often will the alarm go off?

Figuring that out was easy. There are 38 compartments

in a wheel (Fig. 23); so, on average, the ball will light in

Number 8 once every 38 spins. If three minutes elapsed

between spins, the alarm would sound once every 38 x 3 =

114 minutes for each wheel. The casino would have 5

wheels; so the alarm would sound five times this often, or

once every 114 ÷ 5

≅ 23 minutes.

1 wheel: 38

spins

x 3

min

= 114

min

alarm spin alarm

5 wheels: 114

min

÷ 5 = 23

min

alarm alarm

Since the outcome of each spin is entirely random, the

alarm would not, of course, sound at even intervals. There

might be two or three alarms in a matter of minutes, or

none for several hours. But, on average, the time between

alarms would be 23 minutes.

With the exception of the champagne, the parallel

between 8-bell alarms and false alarms on a radar display is

PART III Radar Fundamentals

direct. The probability of a wheel spinning an “8” corre-

sponds to the false-alarm probability of one of the radar’s

threshold detectors; the time between spins, to the integra-

tion time of the radar’s doppler filters; the number of

roulette wheels, to the number of threshold detectors.

In general, a bank of doppler filters is provided for every

resolvable increment of range (range gate), and a threshold

detector is provided for every filter.

Substituting the product of the number of range gates

) times the number of doppler filters per filter bank

) for N in the equation at the top of the facing page

and solving for P

, we get

int

x N

Suppose, for example, that the filter integration time (t

int

) is

0.01 second and the radar has 200 range gates with 512

doppler filters per bank (Fig. 24). To limit the false-alarm

time (t

) to a minute and a half (90 seconds), we would

have to set the threshold of each detector for a false-alarm

probability of about 10

–9

Setting the Detection Threshold. As explained in Chap.

10, the probability of noise crossing the target-detection

threshold depends upon the setting of the threshold relative

to the mean level of the noise. The higher the threshold is,

the lower the probability of a crossing.

Just how high the threshold must be to keep P

from

exceeding the specified value depends, of course, upon the

statistical nature of the noise. Since the nature of thermal

noise is well known and is essentially the same in all situa-

tions, determining the threshold setting that will yield a

given false-alarm probability is comparatively simple. The

statistical characteristics of the noise are usually represented

by what is called a probability density curve (Fig. 25). This

is a plot of the probability that the magnitude of the noise

in the output of a narrowband filter will have a given

amplitude at any one time.

The probability of the noise exceeding the detection

threshold, V

, equals the ratio of (1) the area under the

curve to the right of V

to (2) the total area under the

curve, which is one since by definition the curve encom-

passes all possible magnitudes. This probability, of course,

is the false-alarm probability, P

The area under the thermal-noise curve to the right of V

in Fig. 25 is plotted versus the value of V

in Fig. 26. With a

curve like that, one can readily find the required threshold

setting for any desired P

CHAPTER 11 The Range Equation: What It Does and Doesn’t Tell Us

145

24. Calculation of the detector false-alarm probability that will

limit the time between system false alarms to 90 seconds.

FALSE-ALARM CALCULATION

Problem

Determine the false-alarm probability of a radar's

threshold detectors that will limit the system false-

alarm time to no more than 90 seconds.

Conditions

Filter integration time . . . . . . t

int

= 0.01 second

Number of range gates . . . N

= 200

Number of filters per bank . N

= 512

Calculation

= ≡ 1.09 x 10

-9

int

x N

0.01

90 x 200 x 512

25. Probability density of thermal noise in the output of a narrow-

band filter. Mean noise power σ

= kT

B, where kT

is the

integrated noise energy and B is the filter bandwidth, 1/t

int

26. Area under the thermal-noise probability density curve of

Fig. 25, to the right of the threshold voltage, V

Determining the Required Signal-to-Noise Ratio. The

probability of a target signal plus the noise exceeding the

threshold can similarly be determined. The probability den-

sity of the filter output for a representative signal-to-noise

ratio is plotted in Fig. 27, along with a repeat of the proba-

bility density curve for the noise alone. As with P

in the

case of noise alone, the area under the curve for signal plus

noise to the right of V

is the probability of detection, P

Unlike the fluctuation of the noise, the fluctuation of the

signal—which we have seen is due to the variations in

radar cross section—does not have a simple universal char-

acteristic but varies from one target to the next and from

one operational situation to another. Nevertheless, statisti-

cally it is possible to approximate radar cross sections hav-

ing common characteristics quite accurately with standard

mathematical models.

The required signal-to-noise ratio versus detection prob-

ability for a wide range of false-alarm probabilities has been

calculated for a number of these models. Where specific

radar cross section data is not available or a rigorous calcu-

lation is not required, curves based on these results make

finding the required signal-to-noise ratio easy.

A commonly used set of curves are those based on the

work of a man named Peter Swerling (Fig. 28). They apply

to four different cases. Cases I and II assume a target made

up of many independent scattering elements—as is a large

(in comparison to the wavelength) complex target, such as

an airplane. Cases III and IV assume a target made up of

one large element plus many small independent elements—

as is a small target of simple shape. Cases I and III assume

that the radar cross section fluctuates only from scan to

scan; Cases II and IV assume that it also fluctuates from

pulse to pulse.

With curves such as these, for almost any specified false-

alarm probability, one can quickly find the integrated sig-

nal-to-noise ratio needed to provide any desired detection

28. Standard curves base on simplified radar cross section models

make coarse determination of required signal-to-noise ratio

easy (the signal-to-noise ratio is evaluated at the output of the

doppler filter).

29. The four different cases to which the Swerling models apply.

PART III Radar Fundamentals

146

27. Probability density of filter output for a representative ratio of

signal to noise. Area under curve to right of V

is the proba-

bility of detection, P

. Note that while increasing V

decreas-

es P

, it also decreases P

CASE

FLUCTUATIONS

Scan-Scan

Pulse-Pulse

SCATTERERS

III

Many Independent

One Main

probability. Except for probabilities that are either very high

or very low (and are poorly represented by simplified mod-

els) these curves are extremely useful.

Computing the Range. Having found the integrated sig-

nal-to-noise ratio needed to provide the desired detection

probability, the range at which this ratio will be obtained

can be computed with the equation derived earlier (top of

page 138) for R

. To adapt the equation for this use, the

noise term (kT

) is multiplied by the required signal-to-

noise ratio.

[

avg

σ t

]

(4π)

(S/N)

req

where R

is the range for which the probability of detec-

tion is P

, and (S/N)

req

is the required signal-to-noise ratio.

Cumulative Detection Probability

To account for the effects of closing rate, detection range

is often expressed in terms of cumulative probability of

detection: the probability that a given closing target will

have been detected at least once by the time it reaches a

certain range.

Cumulative probability of detection, P

, is related to sin-

gle-scan probability of detection, P

, as follows.

= 1 – (1 – P

)

where n is the number of scans.

This equation may be readily understood.The term (1–P

)

is the probability of the target not being detected in a given

scan. This term to the n

power, (1 – P

)

, is the probability

of the target not being detected in n successive scans. One

minus that probability is the probability of it being detected

at least once in n scans.

If, for example, P

= 0.3, the probability of the target not

being detected in one scan would be 1 – 0.3 = 0.7. The

probability of it not being detected in ten scans would be

0.7

= 0.03. The probability of it being detected at least

once in 10 scans, therefore, is 1 – 0.03 = 0.97.

But determining the actual probability is not necessarily

as straightforward as that. As the target closes, the value of

will increase. Also, a lot depends on how rapidly the tar-

get cross section (hence the signal) varies. If the rate is

rapid enough for the variation to be essentially random

from one scan to the next, over a period of several scans the

variation will tend to cancel. If P

for the range in question

has a moderate value, as in the foregoing example, P

will

rapidly approach 100 percent.

CHAPTER 11 The Range Equation: What It Does and Doesn’t Tell Us

147

SAMPLE RANGE COMPUTATION

Problem: Find the range at which the proba-

bility of a given pulse-doppler radar detecting

a given target is 50%.

Characteristics Of The Radar:

Average Power (P

avg

) . . . . . . . . . . 5 kW

Effective Area of Antenna (A

). . . . 4 ft

Wavelength (λ) . . . . . . . . . . . . . . . 0.1 ft

Receiver Noise Figure (F

) . . . . . . 3 dB

Total losses (L) . . . . . . . . . . . . . . . 6 dB

Target: Fighter, viewed head-on, at constant

look angle. Radar Cross Section, σ = 10 ft

Operating Conditions: Radar is searching a

solid angle 100° wide in azimuth by 10° wide

in elevation. The radar beam's time on target,

= 0.03 second.

Solution: Only two more values are needed

to compute the range: the required signal-to-

noise ratio, (S/N)

req

, and the noise energy,

Since the target is not very large and is

viewed head-on from a constant angle, it's

RCS will probably not fluctuate from pulse to

pulse in the 0.03 second time on target. So, a

rough estimate of (S/N)

req

can be obtained

from Swerling's Case 1 curve in Figure 28. It

indicates that for a probability of detection of

50%, (S/N)

req

is about 10 dB.

The value of kT

, can be obtained by multi-

plying kT

—which, as shown on page 118,

equals 4 x 10

-21

—by the receiver noise figure,

3dB (factor of 2). Thus, kT

= 8 x 10

-21

Plugging the above values into the equation

for R

(with the loss term, L, included in the

denominator) yields:

avg

σ t

(4π)

(S/N)

req

1/4

(5 x 10

)

x 4

x 10 x 0.03

158 x 10 x (8 x 10

-21

) x 0.1

x 4

1/4

= 4.67 x 10

ft = ≡78 nmi

4.67 x 10

6 x 10

PART III Radar Fundamentals

148

THE MANY FORMS OF THE RADAR RANGE EQUATION

The many different forms of the equation for signal-to-noise

ratio are easily confusing. To help you keep them straight in your

mind, the constituent expressions for four of them are summa-

rized here.

Area of sphere ⫽ 4π R

Antenna gain, G ⫽

4π A

Click for high-quality image

• Range at which integrated signal-to-noise

ratio is 1:

Spotlight

Volume

• False-alarm time:

• False-alarm time for a single detector:

• Range for which probability of detection is P

• Cumulative probability of detection

= 1 – (1 – P

)

= =

Fale-alarm rate

1 t

int

N = number of threshold detectors

int

x N

= number of range gates

= doppler filters per bank

avg

σ t

int

k T

= P

avg

Some Relationships To Keep In Mind

avg

σ t

1/4

(4π)

(S/N)

req

(S/N)

req

= required signal-to-noise ratio

On the other hand, if there is little change in cross sec-

tion from scan to scan and the target happens to be in a

deep fade, the cumulative probability of detection for the

same range may be quite low.

Summary

From the expressions for signal energy and noise energy

a simple equation for detection range may be derived. It

tells us that

• Range increases as the

4th power of average transmit-

ted power, target radar cross section, and integration

time

• Range increases as the square root of effective antenna

area

• A reduction in noise is equivalent to a proportional

increase in transmitted power

When adapted to the special case of volume search, the

equation tells us that to the first order, range is independent

of frequency and can be maximized by using the highest

possible average power and the largest possible antenna.

Even when all secondary factors influencing signal-to-

noise ratio have been accounted for, the range equation

cannot tell us with certainty at what range a given target

will be detected, since both noise and radar cross section

fluctuate widely.

Consequently, detection range is usually specified in

terms of probabilities. The most common probability for

search is blip-scan ratio (also called single-scan or single-

look probability). The range at which a given value of this

probability may be achieved is determined by (1) establish-

ing an acceptable false-alarm probability, (2) setting the tar-

get detection threshold just high enough to realize this

probability, and (3) finding the signal-to-noise ratio for this

setting that will provide the desired target detection proba-

bility, a process which may be simplified through the use of

curves based on standard mathematical models of targets.

The range at which that ratio will be achieved is then calcu-

lated with the range equation.

To account for the effect of closing rate in high-closing

rate approaches, detection range may be expressed in terms

of cumulative probability of detection—the probability that

a given target will be detected at least once before it reaches

a given range.

CHAPTER 11 The Range Equation: What It Does and Doesn’t Tell Us

149