George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

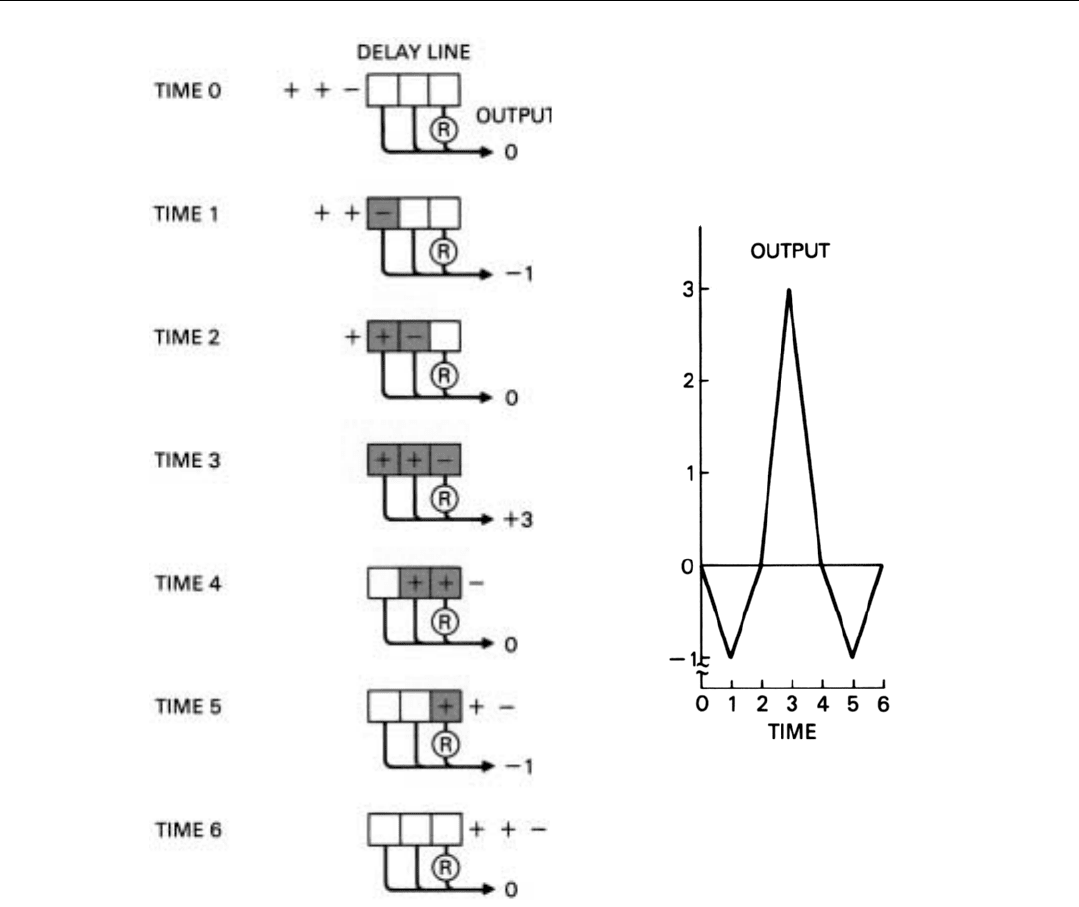
segment (Fig. 15). Since its phase is 180˚, the output is

negative: – 1.

An instant later, Segment No. 2 has entered the line.

Now the output signal equals the sum of Segments No. 1

and No. 2. Since the segments are 180˚ out of phase, how-

ever, they cancel: The output is 0.

When Segment No. 3 has entered the line, the output

signal is the sum of all three segments. Segment No. 1, you

will notice, has reached a point in the line where the tap

contains a phase reversal. The output from this tap, there-

fore, is in phase with unshifted Segment No. 2. The phase

of Segment No. 3 also being unshifted, the combined out-

put of the three taps is three times the amplitude of the

individual segments: +3.

CHAPTER 13 Pulse Compression

171

15. Step-by-step progress of a 3-digit binary phase modulated pulse through a tapped delay line.

PART III Radar Fundamentals

172

As Segments No. 2 and No. 3 pass through the line, this

same process continues. The output drops to zero, then

increases to minus one, and finally returns to zero again.

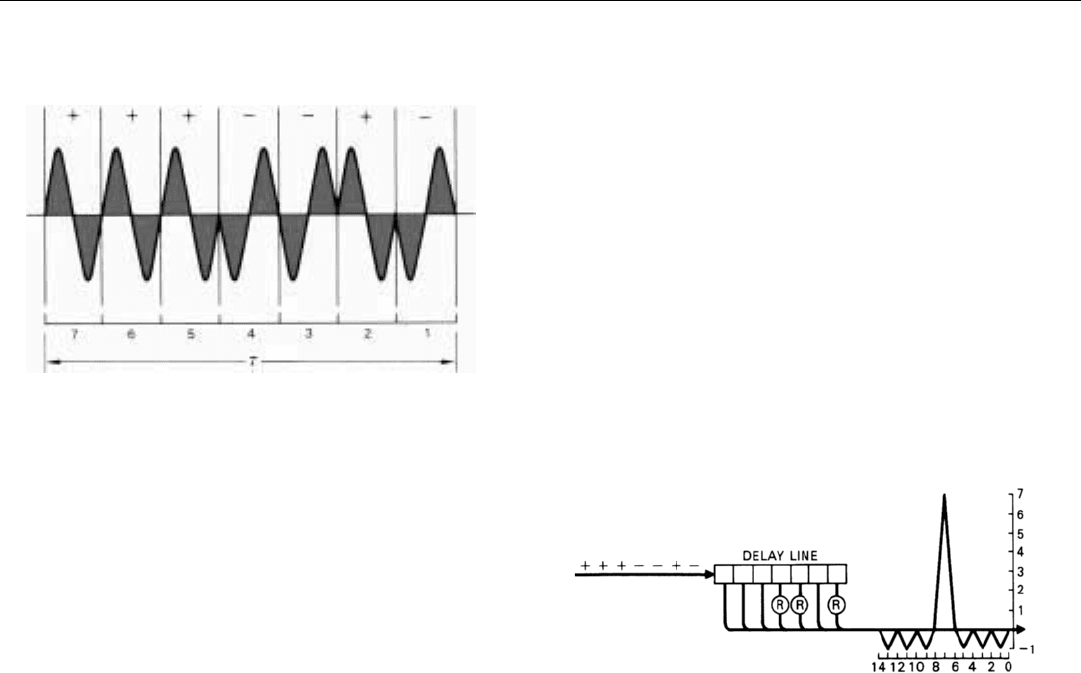
A somewhat more practical example is shown in Fig. 16.

This code has seven digits. Assuming no losses, the peak

amplitude of the compressed pulse is seven times that of

the uncompressed pulse, and the compressed pulse is only

one-seventh as wide.

To see why the code produces the output it does, transfer

the code to a sheet of paper and slide it across the delay line

plotted in Fig. 17 (below), digit by digit, noting the sum of

the outputs for each position. (A minus sign, –, over a tap

with a reversal

in it, becomes a +; and a + becomes a –.)

You should get the output shown in the figure.

16. A seven-digit binary phase code.

17. Output produced when seven-digit phase code is passed through

tapped delay line with phase reversals in appropriate taps.

Sidelobes. Ideally, for all positions of the echo in the line—

except the central one—the outputs from the same number of

taps would have phases of 0˚ and 180˚. The outputs would

then cancel, and there would be no range sidelobes.

One set of codes, called the Barker codes, comes very

close to meeting this goal (Fig. 18). Two of these have been

used in the examples. As you have seen, they produce side-

lobes whose amplitudes are no greater than the amplitude

of the individual segments. Consequently, the ratio of main-

lobe amplitude to sidelobe amplitude, as well as the pulse

compression ratio, increases with the number of segments

into which the pulses are divided—i.e., the number of dig-

its in the binary code.

Unfortunately, the longest Barker code contains only 13

digits. Other binary codes can be made practically any

length, but their sidelobe characteristics, though reasonably

good, are not quite so desirable.

Complementary Barker Codes. It turns out that the four-

digit Barker code has a special feature which enables us not

only to eliminate the sidelobes altogether but to build codes

of great length.

18. Barker codes come very close to the goal of producing no

sidelobes. But the largest code contains only 13 digits.

N BARKER CODES

2   OR ( )

3   

4     OR (     )

5     

7       

11           

13            

Note: Plus and minus signs may be interchanged

(    changed to    ); order of digits may be reversed

(    changed to    ). Codes in parentheses are

complementary codes.

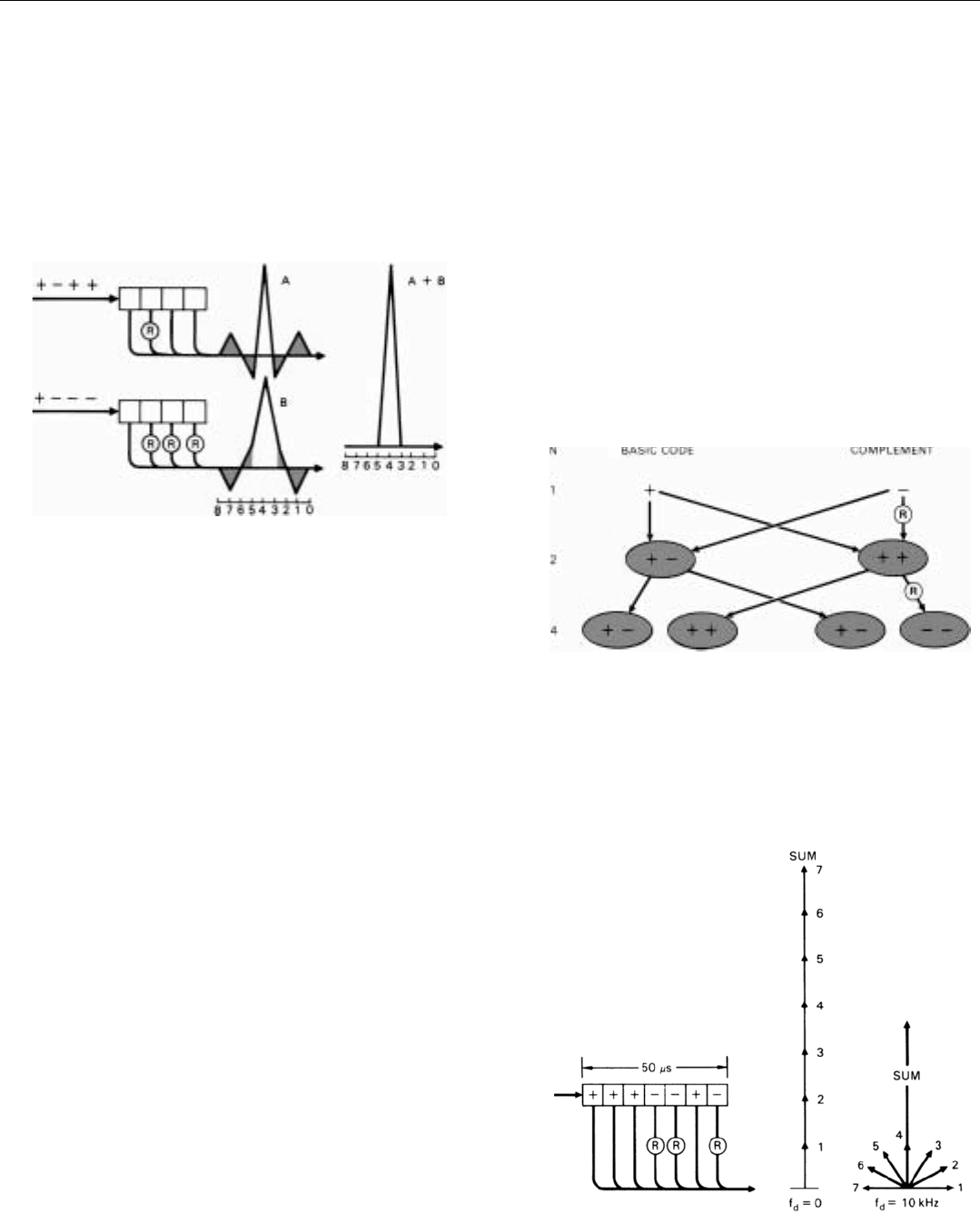
This code, and also the two-digit code, have comple-

mentary forms. Corresponding sidelobes produced by the

two forms have opposite phases. Therefore, it we alternately

modulate successive transmitted pulses with the two forms

of the code—and appropriately switch the locations of the

phase reversals in the outputs of the delay line, for alternate

interpulse periods—when the returns from successive puls-

es are integrated the sidelobes cancel (Fig. 19).

CHAPTER 13 Pulse Compression

173

19. Echoes with complementary phase coding, received from same tar-

get during alternate interpulse periods. When echoes are integrat-

ed, time sidelobes cancel.

20. How complementary codes are formed. Basic two-digit code

is formed by chaining basic binary digit (+) to its complement

(–), Complementary two-digit code is formed by chaining

basic binary digit (+) to its complement with sign reversed (+).

Basic four-digit code is formed by chaining basic two-digit

code to complementary two-digit code. Complementary four-

digit code is formed by chaining basic two-digit code to com-

plementary two-digit code with sign reversed, and so on.

More importantly, by chaining the complementary forms

together according to a certain pattern, we can build codes

of almost any length. As illustrated in Fig. 20, the two forms

of the four-digit code are just such combinations of the two

forms of the two-digit code; and these are just such combi-

nations of the two fundamental binary digits, + and –.

Unlike the unchained Barker codes, the chained codes

produce sidelobes having amplitudes greater than one. But

since the chains are complementary, these larger sidelobes—

like the others—cancel when successive pulses are integrat-

ed.

Limitations of Phase Coding. The principal limitation of

phase coding is its sensitivity to doppler frequencies. If the

energy contained in all segments of a phase-coded pulse is

to add up completely when the pulse is centered in the

delay line, while cancelling when it is not, very little shift in

phase over the length of the pulse can be tolerated, other

than the 180˚ phase reversal due to the coding.

As will be explained in Chap. 15, a doppler shift is actu-

ally a continuous phase shift. A doppler shift, of, say, 10

kilohertz amounts to a phase shift of 10,000 x 360˚ per sec-

ond, or 3.6˚ per microsecond. If the radar’s pulses are as

much as 50 microseconds long (Fig. 21), this shift will itself

equal 180˚ over the length of the pulse, and performance

will deteriorate. For the scheme to be effective, either the

21. Reduction in peak output of tapped delay line for 50

microsecond, phase-coded pulse, resulting from doppler shift

of 10 kilohertz.

PART III Radar Fundamentals

174

doppler shifts must be comparatively small or the uncom-

pressed pulses reasonably short.

Polyphase Codes

Phase coding is not, of course, limited to just two incre-

ments (0˚ and 180˚). Codes employing any number of dif-

ferent, harmonically related phases may be used—e.g., 0˚,

90˚, 180˚, 270˚. One example is a family called Frank

codes.

The fundamental phase increment, φ, for a Frank code is

established by dividing 360˚ by the number of different

phases to be used in the code, P. The coded pulse is then

built by chaining together P groups of P segments each.

The total number of segments in a pulse, therefore, equals

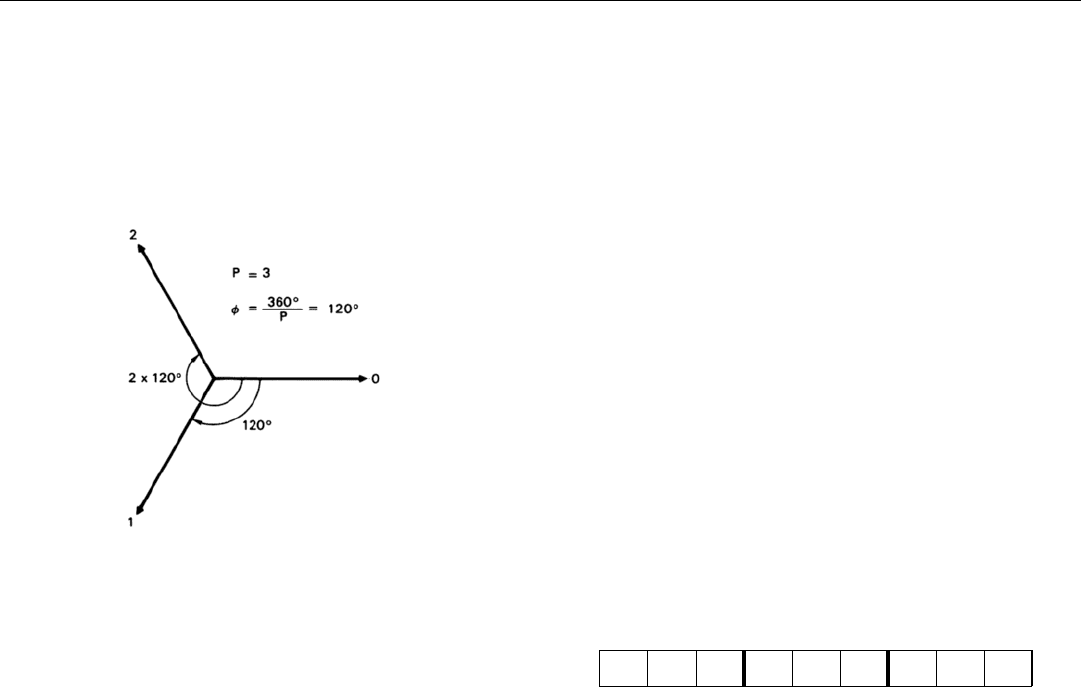
In a three-phase code (Fig. 22), for example, the funda-

mental phase increment is 360˚ ÷ 3 = 120˚, making the

phases 0˚, 120˚, and 240˚. The coded pulse consists of three

groups of three segments—a total of 9 segments.

Group 1 Group 2 Group 3

Phases are assigned to the individual segments according

to two simple rules. (1) The phase of the first segment of

every group is 0˚. That is, 0˚ __ __, 0˚ __, __, 0˚ __, __.

(2) The phases of the remaining segments in each group

increase in increments of

∆Φ = (G – 1) x (P – 1) x φ˚

where G is the group number and φ is the basic increment.

For a three-phase code (P = 3, φ = 120˚, P – 1 = 2), then

∆Φ = (G – 1) x 2φ. So the phase increment in Group 1 is

0˚, the phase increment for Group 2 is 2φ, and the phase

increment for Group 3 is 4φ.

Written in terms of φ, the nine digits of the code for P = 3

thus are

Group 1 Group 2 Group 3

0, 0, 0, 0, 2φ, 4φ, 0, 4φ, 8φ

Substituting 120˚ for φ and dropping multiples of 360˚,

the code becomes

Group 1 Group 2 Group 3

0˚, 0˚, 0˚, 0˚, 240˚, 120˚, 0˚, 120˚, 240˚

22. Phase increments for a Frank code in which number of phas-

es, P, is three.

2. This constraint may in some

cases be circumvented through

“doppler tuning,” a technique

whereby the doppler shift is

largely removed before the

pulses are passed through the

compression filter.

∆Φ = (G – 1) x (P – 1) x φ˚

G = group

P = number of phases

φ = basic phase increment

Echoes are decoded by passing them through a tapped

delay line (or the digital equivalent) in the same way as

binary-phase-coded echoes (Fig. 23). The only difference:

the phase shifts in the taps have more than one value.

For a given number of segments, a Frank code provides

the same pulse compression ratio as a binary phase code

and the same ratio of peak amplitude to sidelobe amplitude

as a Barker code. Yet, by using more phases (increasing P),

the codes can be made any length. As P is increased, how-

ever, the size of the fundamental phase increment decreas-

es, making performance more sensitive to externally intro-

duced phase shifts and imposing more severe restrictions

on uncompressed pulse width and maximum doppler shift.

Summary

The commonly used pulse compression techniques are lin-

ear frequency modulation (chirp) and binary phase coding.

In chirp, the frequency of each transmitted pulse is con-

tinuously increased or decreased. Received pulses are

passed through a filter, which introduces a delay that

decreases or increases with frequency. Successive increments

of a pulse, therefore, bunch up. Width of the compressed

pulse is 1/∆F, where ∆F is the total change in frequency.

The pulse has sidelobes, but they can be acceptably

reduced by tapering the amplitude of the uncompressed

pulse.

When only a narrow range swath is of interest, chirp can

be decoded with stretch radar techniques, whereby range is

converted to frequency. Differences in frequency are

resolved by a bank of fixed-tuned filters, implemented with

the efficient fast Fourier transform.

CHAPTER 13 Pulse Compression

175

23. Processing of Frank codes is similar to that of binary codes. Phase shifts introduced in taps complement shifts in corresponding segments of

coded pulse. If phase of a segment is shifted by 1 x 120

˚, corresponding tap adds a shift of 2 x 120˚, making total shift when pulse fills

line equal 3 x 120˚ = 360˚.

PART III Radar Fundamentals

176

Chirp has the advantage of providing large compression

ratios and being simple.

In binary phase modulation, each pulse is marked off

into segments, and the phase of certain segments is

reversed. Received pulses are passed through a tapped

delay line having phase reversals in corresponding taps.

The output pulse is the width of the segments. It, too, has

sidelobes.

With Barker codes the mainlobe-to-sidelobe ratio equals

the pulse-compression ratio, but the longest code is only 13

digits. Sidelobes can be eliminated by alternately transmit-

ting complementary forms of the four-digit code. These can

be chained to any length. But, if doppler shifts are large,

performance deteriorates unless pulses are reasonably

short.

Polyphase—e.g., Frank—codes can also be used, but

they are even more sensitive to doppler frequency.

177

FM Ranging

f enough PRFs can be provided to resolve the growing

number of range ambiguities that arise as the PRF is

increased, pulse delay ranging can be employed suc-

cessfully even at fairly high PRFs. However, a point is

ultimately reached where the echoes return so “thick and

fast” it is virtually impossible to resolve the ambiguities

(Fig. 1). Range, if required, must then be measured indi-

rectly, as in CW radars. The most common indirect

method is linear frequency modulation, or FM, ranging.

This chapter briefly describes the principle of FM rang-

ing. It explains how doppler frequency shifts, which would

otherwise introduce gross measurement errors, are taken

into account and how a problem of ghosting similar to that

encountered in PRF switching is handled. Finally, it briefly

considers the accuracy which may be obtained with FM

ranging.

Basic Principle

With FM ranging, the time lag between transmission

and reception is converted to a frequency difference. By

measuring it, the time lag—hence the range—is deter-

mined.

In simplest form, the process is as follows. The radio

frequency of the transmitter is increased at a constant

rate. Each successive transmitted pulse thus has a slightly

higher radio frequency. The linear modulation is contin-

ued for a period at least several times as long as the round-

trip transit time for the most distant target of significance

(Fig. 2). Over the course of this period, the instantaneous

difference between the frequency of the received echoes

1. If the PRF is increased beyond a certain point, it becomes

impractical, if not impossible, to resolve range ambiguities.

Ranging time must then be measured indirectly.

2. In simplest form, FM ranging involves changing the transmitter

frequency at a constant rate. Length of slope is generally

many times maximum round-trip transit time.

1. Another form of FM ranging

which has advantages in

some applications employs

sinusoidal modulation.

PART III Radar Fundamentals

178

and the frequency of the transmitter is measured. The

transmitter is then returned to the starting frequency, and

the cycle is repeated.

Just how the measured frequency difference is related to

a target’s range is illustrated in Fig. 3 for a static situation.

That is a situation, such as a tail chase, where the range

rate is zero.

In this figure, the radio frequency of both the transmit-

ter and the echoes received from a target are plotted versus

time. The dots on the plot of transmitter frequency represent

individual transmitted pulses. The horizontal distance

between each of these dots and the dot representing the

received target echo is the round-trip transit time. The ver-

tical distance between the echo dot and the line represent-

ing the transmitter frequency is the difference, ∆f, between

the frequency of the echo and the frequency of the trans-

mitter when the echo is received.

As you can see, this difference equals the rate of change

of the transmitter frequency—hertz per microsecond—

times the round-trip transit time. By measuring the fre-

quency difference and dividing it by the rate (which we

already know), we can find the transit time.

Suppose, for example, that the measured frequency dif-

ference is 10,000 hertz and the transmitter frequency has

been increasing at a rate of 10 hertz per microsecond. The

transit time is

10,000 Hz

= 1,000 µs

10 Hz/µs

Since 12.4 microseconds of round-trip transit time corre-

spond to one nautical mile of range, the target’s range is

equal to 1000 ÷ 12.4 = 81 nautical miles.

3. Difference between the frequency of an echo and the frequen-

cy of the transmitter at the time an echo is received (

∆f) is

proportional to transit time (t

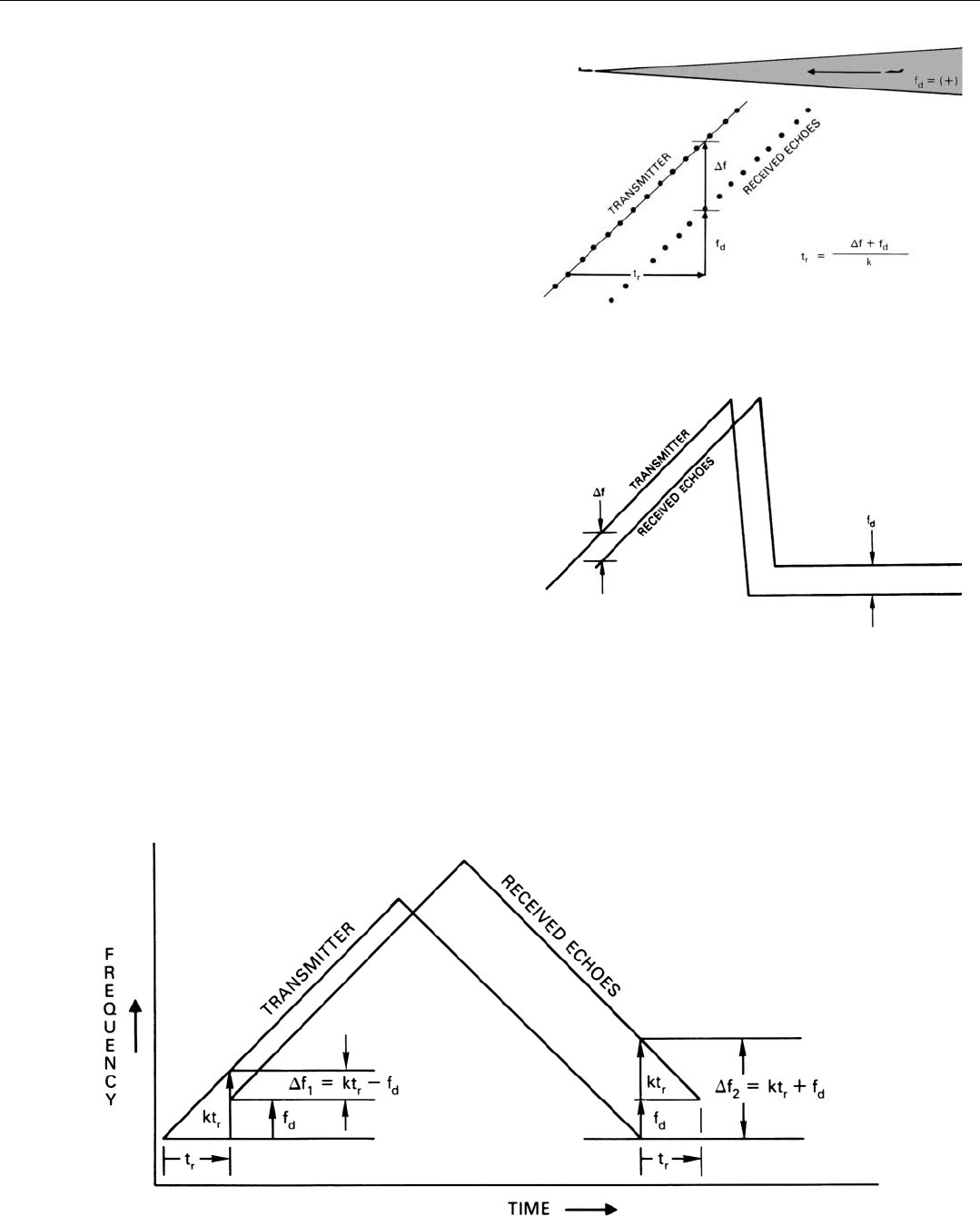
Accounting for the Doppler Shift

Actually, the process is more complicated than just out-

lined, for the range rate rarely is zero. The frequency of a

target echo is not equal solely to the frequency of the trans-

mitted pulse that produced it, but to that frequency plus

the target’s doppler frequency. To find the transit time, we

must add the doppler frequency, f

, to the measured fre-

quency difference (Fig. 4).

Including a Constant-Frequency Segment. As you may

have surmised, the doppler frequency can be found by

interrupting the frequency modulation at the end of each

cycle and transmitting at a constant frequency for a brief

period. During this period, the difference between the echo

frequency and the transmitter frequency will be due solely

to the target’s doppler frequency. By measuring that differ-

ence (Fig. 5) and adding it to the difference measured dur-

ing the sloping segment, we can find the transit time.

Alternate, Two-Slope Cycle. It turns out that the doppler

frequency can be added just as easily by employing a two-

slope modulation cycle. The first slope is the same as the

rising-frequency slope just described. Once it has been tra-

versed, the frequency is decreased at the same rate until the

starting frequency is again reached (Fig. 6 below). The cycle

is then repeated.

If the target is closing—i.e., has a positive doppler fre-

quency, f

—the difference between the frequency of the

transmitter and the frequency of the received echoes will be

decreased by f

during the rising-frequency segment and

increased by f

during the falling-frequency segment. (The

CHAPTER 14 FM Ranging

179

6. With two-slope modulation, frequency difference is decreased by f

during rising slope and increased by f

during rising slope and

increased by f

during falling slope.

4. Frequency difference, ∆f, between transmitter and received

echoes is reduced by target’s doppler frequency, f

. To find

transit time, f

must be added to ∆f.

5. Target’s doppler frequency (f

) may be measured by adding a

constant frequency segment to the modulation cycle.

PART III Radar Fundamentals

180

reverse will be true if the target is opening.) Consequently,

if the frequency differences for the two segments are added,

the doppler frequency will cancel out.

∆f

= kt

– f

∆f

= kt

+ f

∆f

+ ∆f

= 2kt

+ 0

The sum, then, will be twice the frequency difference,

, due to the round-trip transit time. The latter can be

found by dividing the sum by twice the rate of change of

the transmitter frequency.

∆

where

= round-trip transit time

∆

= difference between transmitter and echo

frequencies during rising-frequency seg-

ment

∆f

= difference between transmitter and echo

frequencies during falling-frequency seg-

ment

k = rate of change of transmitter frequency

Again, knowing the transit time, we can readily calculate

the target range.

Suppose the target used in the previous example (k = 10

Hz/µs, kt

= 10 kHz) had a doppler frequency of 3 kilo-

hertz. During the rising-frequency segment, the measured

frequency difference would have been 10 – 3 = 7 kHz.

During the falling-frequency segment, it would have been

10 + 3 = 13 kHz. Adding the two differences and dividing

by 2 k (20 Hz / µs second) gives the same transit time, 1000

microseconds, as when the doppler frequency was zero.

Although in both this example and the illustrations the

doppler frequency is positive, the equation works just as

well for negative doppler frequencies.

Eliminating Ghosts

If the antenna beam encompasses two targets at the same

time, a problem of ghosting may be encountered, as with

PRF switching. There will be two frequency differences dur-

ing the first segment of the modulation cycle and two dur-

ing the second (Fig. 7). This is true, of course, regardless of

whether both segments are sloped or one is sloped and the

other is not.

7. If two targets are detected simultaneously, two frequency dif-

ferences will be measured during each segment of the cycle.

7kHz + 13 kHz

2 X .01 KHz/µs

20 kHz

.02 kHz/µs

= 1,000 µs