George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

CHAPTER 16 Spectrum of Pulsed Signal

203

10. Coherent pulses produce output from receiver at evenly

spaced intervals of frequency.

11. Spectral lines of coherent signal fit within envelope having

same shape (sin x /x) as spectrum of noncoherent pulse train

having equal pulsewidth, τ.

The effect of changing to coherent transmission is

remarkable, to say the least (Fig. 10). Whereas, with nonco-

herent transmission, the signal’s central spectral lobe is

spread over a broad band of frequencies, with coherent

transmission, it peaks up almost as sharply as the continu-

ous wave did. There is, however, one important difference.

Instead of appearing at only one point on the radio dial, the

coherent pulsed signal appears at many different points. Its

spectrum, in fact, consists of a series of evenly spaced lines.

Comparing this spectrum with the corresponding spec-

trum for the noncoherent signal—same PRF and same

pulse width—we observe two things. First, at those fre-

quencies where the coherent signal produces an output, it

is a great deal stronger than the output produced by the

noncoherent signal, evidently because the energy has been

concentrated into a few narrow lines. Second, the “enve-

lope” within which these lines fit (Fig. 11) has the same

shape (sin x/x) and the same null-to-null width (2/τ) as the

spectrum of the noncoherent signal.

Suspecting that the spacing of the lines is related to the

PRF, we repeat the experiment several times, at progressive-

ly higher PRFs. As the PRF is increased, the lines move far-

ther apart. In every case, the spacing exactly equals the PRF

(Fig. 12).

Incidentally, it may be instructive to note that since we

maintained a constant pulse width, as we increased the PRF

the number of lines decreased. Had we continued to

increase the PRF, a point would ultimately have been

reached where all of the power was concentrated into a sin-

gle line. But then we would be transmitting a CW signal.

The important conclusion to be drawn from this experi-

ment, though, is that the spectrum of a coherent pulsed sig-

nal consists of a series of lines that (1) occur at intervals

equal to the PRF on either side of f

and (2) fit within an

envelope having a sin x/x shape with nulls at multiples of

1/τ above and below f

In one significant respect, however, this experiment was

not realistic insofar as the operation of a great many radars

is concerned. For each dial setting, the train of received

pulses was at least several seconds long. In fact, for each

new setting of the tuning dial, we had to wait several sec-

onds for the receiver output meter to reach its final reading.

By contrast, the train of pulses a search radar receives each

time its beam sweeps across a target may be only a small

fraction of a second long.

As we shall see, unless a pulse train is infinitely long—

which no pulse train we will ever encounter could possibly

be—the spectral lines have a finite width. This width is a

function of the duration of the pulse train.

12. Spacing of spectral lines for a coherent pulse train equals

PRF, f

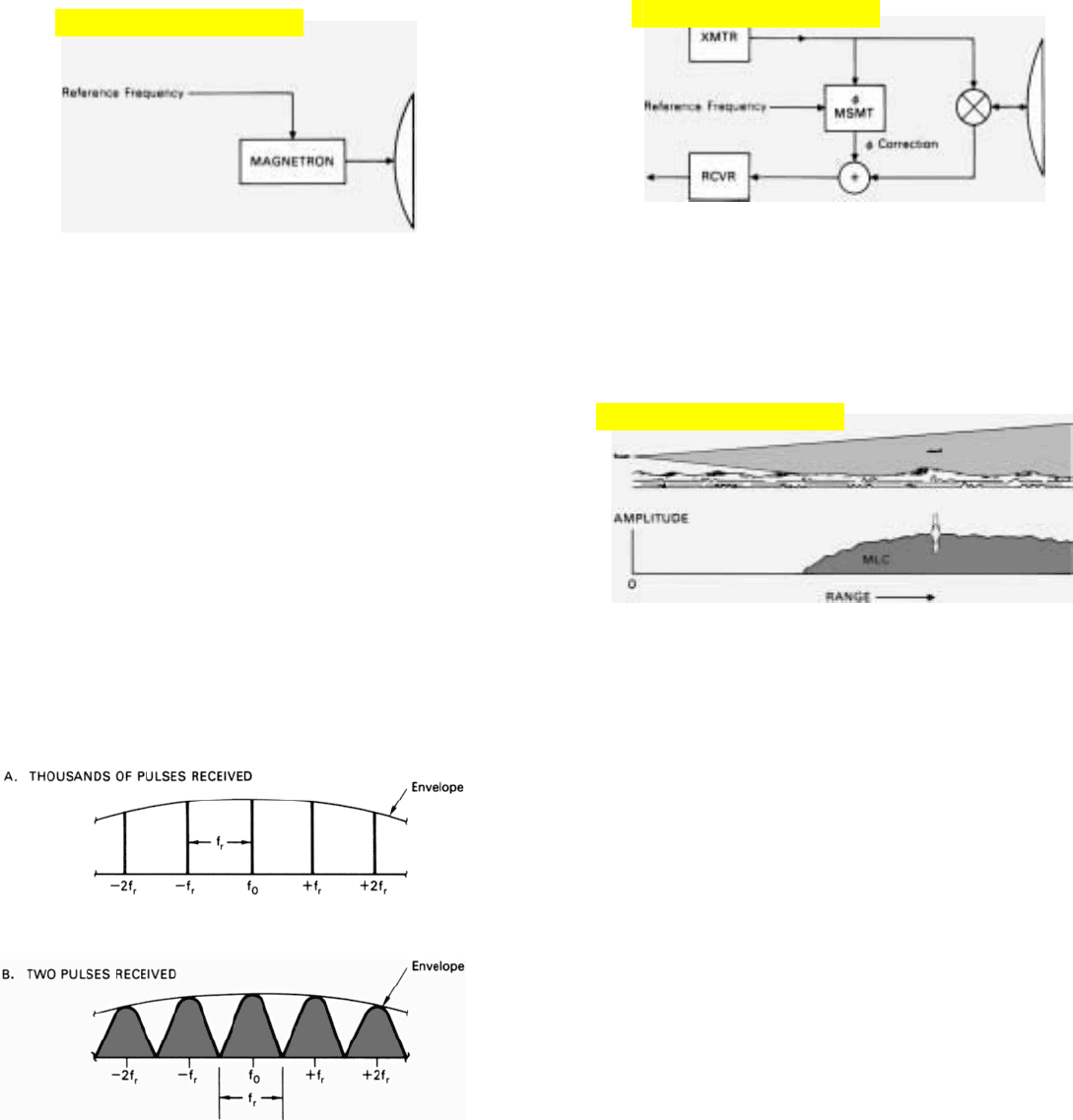
13. Whereas when thousands of pulses are received, spectral

lines are narrow and sharply defined, when only two pulses

are received, spectral lines broaden until they are contiguous.

PART III Radar Fundamentals

204

Line Width versus Duration of Pulse Train

To find the relationship between line width and the

length of a pulse train, we perform two more experiments.

Experiment No. 4: Two-Pulse Train. For this experi-

ment, we use the same receiver and coherent transmitter as

before. But, holding the PRF constant, we transmit only two

pulses for each setting of the tuning dial.

The results are shown in Fig. 13, along with a repeat of

the results of Experiment No. 3, for the same PRF and pulse

width.

Whereas, when the pulse train was a thousand or more

pulses long, the receiver output peaked up sharply at each

multiple of the PRF; when it is only two pulses long, the

plot of receiver output versus frequency is almost continu-

ous. The output still reaches its maximum values at multi-

ples of the PRF and falls off on either side of each peak, but

it only reaches zero halfway between peaks. The null-to-

null “line width” is f

hertz!

EARLIER METHODS OF ACHIEVING COHERENCE

Largely because the master oscillator—power amplifier was

expensive to implement with the components then available, in

the early airborne doppler radars various other techniques were

used to achieve coherence. Some of these are still in use today.

In one, called injection locking, the starting phase of a simple

transmitter such as a magnetron is “locked” to the phase of a

highly stable, continuously generated low power signal that is

injected into the magnetron cavity.

In another, called coherent-on-receive, or COR, one measures the

phase of each transmitted pulse relative to a continuously gener-

ated reference signal. An appropriate phase correction is then

applied to the return received during the immediately following

interpulse period.

Unfortunately, with injection locking, the degree of coherence gen-

erally leaves something to be desired. And with coherent-onre-

ceive, only the first-time-around return is coherent, since the

phase correction is only valid for return from the immediately

preceding transmitted pulse.

In still another approach, called noncoherent or clutter-referenced

moving target indication, the equivalent of coherence is achieved

by detecting the “beat” between the target echoes and the

simultaneously-received ground return. But as explained in page

24 in Chapter 2, this technique has serious limitations.

COHERENT ON RECEIVE (COR)

Click for high-quality image

Experiment No. 5: Eight-Pulse Train. We repeat the

experiment, using the same PRF and pulse width, but this

time transmitting four times as many pulses for each dial

setting—eight as opposed to two. Although the signal still

produces an output over a fairly broad band around each

multiple of the PRF (Fig. 14) the spectral lines are now

only one-fourth as wide—f

/4 hertz as opposed to f

hertz.

General Relationships. From the results of these two

experiments, we conclude that the width of the spectral

lines is inversely proportional to the number of pulses in the

pulse train. Since for two pulses the line width equals the

PRF, we further conclude that for N pulses it equals (2 / N)

times the PRF.

(

)

where

= null-to-null line width

= pulse repetition frequency

N = number of pulses in the train

If, for example, a pulse train contains 32 pulses, the line

width is 2/32, or one-sixteenth, of the PRF.

The primary factor upon which line width depends how-

ever is not just the number of pulses, but the duration of

the pulse train—its length in seconds. This becomes clear

if we replace f

in the expression for LW

with 1/T, where

T is the interpulse period. The expression then becomes

= 2/(NT). Since N is the number of interpulse periods

in the train, NT is the train’s total length. Accordingly,

Length of train (seconds)

Equivalence of Pulse Train to Long Pulse. Interestingly,

the results of this experiment are consistent with those of

Experiment No. 2. They indicated that the null-to-null

bandwidth for a single pulse is two divided by the length of

the pulse in seconds: BW

= 2/τ. If we were to transmit a

single pulse, the length of a train of N pulses, its null-to-

null bandwidth would be exactly the same as the null-to-

null line width of the pulse train (Fig. 15). Thus, there is

only one difference between the spectrum of a train of

coherent pulses and the spectrum of a single pulse the

same length as the train: the spectrum of the pulse train is

repeated at intervals equal to the PRF.

The parallel between the spectra of a coherent pulse train

and a single long pulse is noted here for two reasons. First,

it makes remembering the spectrum of a pulsed signal a bit

easier. Second, it will prove illuminating when we take up

the explanation of the pulsed spectrum, in the next chapter.

CHAPTER 16 Spectrum of Pulsed Signal

205

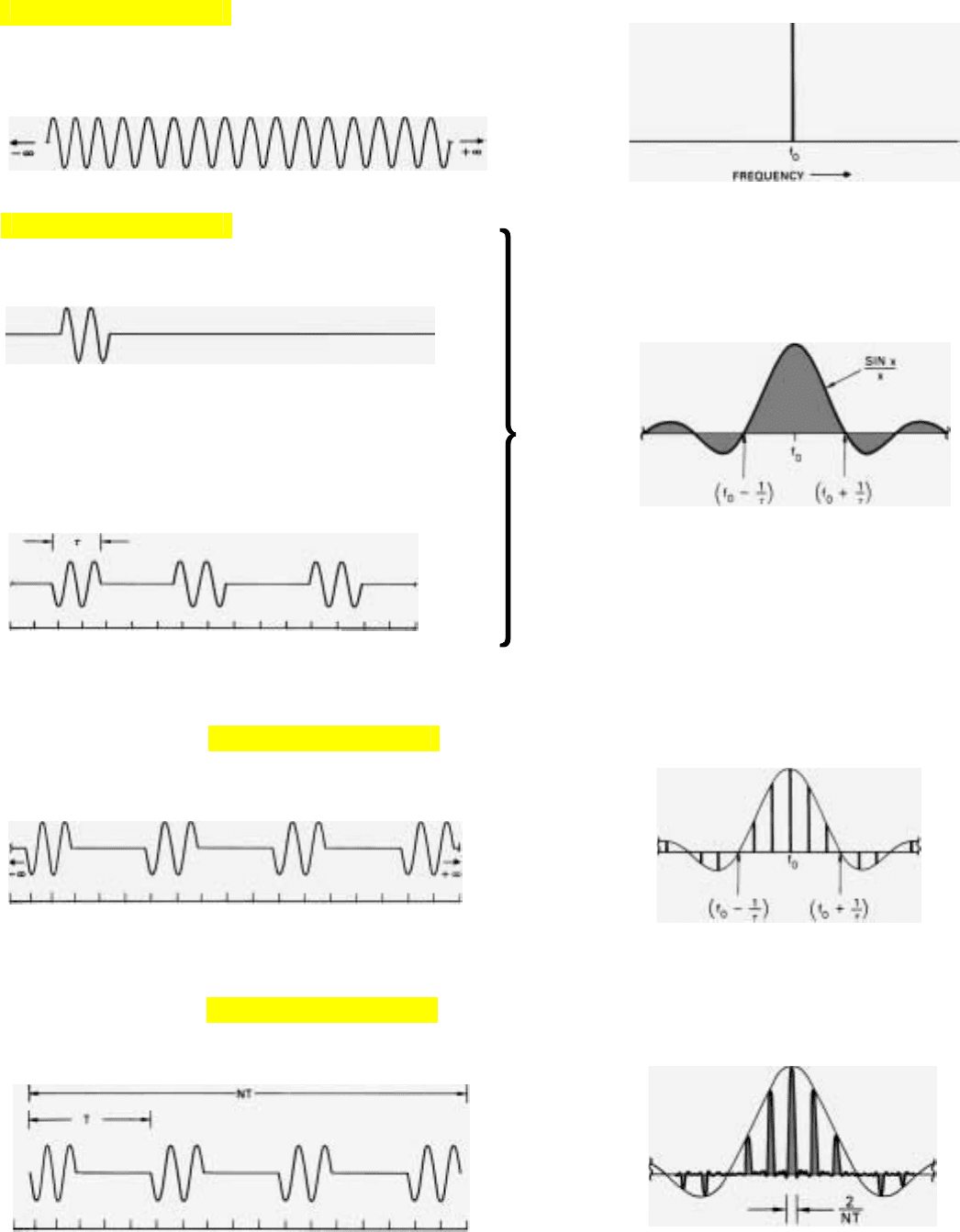
14. When eight pulses (instead of two) are received, null-to-null

width of spectral lines is only one-fourth as great.

15. Individual spectral lines for a coherent pulse train differ from

the spectrum of a single pulse of the same length only in

being repeated at intervals equal to the PRF (f

∴

Click for high-quality image

PART III Radar Fundamentals

206

Spectral Sidelobes

What about spectral sidelobes? Just as they flank the

mainlobe of the spectrum of a single pulse, sidelobes of half

the null-to-null line width flank each “line” of the spectrum

of a pulse train (Fig. 16). The line itself has a sin x/x shape.

Since the length of the train of pulses received from a

target during any one scan of the radar antenna is invari-

ably limited, the sidelobes are an important concern to the

radar designer. For they tend to fill in the gaps between the

spectral lines. Fortunately, as will be explained in Chap. 19,

by suitably designing the doppler filters of the radar’s signal

processor, the sidelobes can generally be reduced to an

acceptable level.

Conclusions Drawn from the Experiments. The conclu-

sions we have drawn from our five simple experiments are

summarized graphically in the panel on facing page. By way

of underscoring their significance, let us return to the ques-

tion raised earlier in this chapter: If the spectral width of a

radar pulse may be many times the highest doppler fre-

quency, how can a pulsed radar discern small doppler shifts

in what may be extremely weak target return buried in

strong ground clutter?

In light of the illustrations in the panel, the answer

should be abundantly clear. A pulsed radar can readily dis-

cern these shifts if the following conditions are satisfied:

• The radar is coherent.

• The PRF is high enough to spread the lines of the

spectrum reasonably far apart.

• The duration of the pulse train is long enough to

make the lines reasonably narrow.

• The doppler filters are suitably designed to reduce the

spectral sidelobes.

As will be borne out in subsequent chapters, detecting

doppler shifts under typical operating conditions may be a

bit more involved than implied here. But the crux of the

matter is satisfying these basic requirements.

Summary

Transmitting a radio frequency signal in pulses markedly

changes in the signal’s spectrum, as observed by the tuned

circuit of a receiver.

Whereas the spectrum of a continuous wave of constant

wavelength consists of a single line, the spectrum of a single

pulse of the same wavelength covers a band of frequencies

and has a sin x /x shape. The width of the central lobe of

16. Just as sidelobes flank the central spectral lobe of a single

pulse, they also flank each line in the spectrum of coherent

pulse train.

2. If ranges are extremely long it

is possible to transmit perfect-

ly coherent pulses and have

some loss of coherence in the

medium through which the

waves propagate.

CHAPTER 16 Spectrum of Pulsed Signal

207

RESULTS OF THE EXPERIMENTS

Continuous Wave (CW)

Infinite Length

Single Pulse

Train of Noncoherent Pulses

(Random starting phases)

Train of Coherent Pulses

Infinite Length

Train of Coherent Pulses

Limited Length

Click for high-quality image

PART III Radar Fundamentals

208

this spectrum varies inversely with pulse width. If the puls-

es are as narrow as those used in many radars, the central

lobe may be several megahertz wide.

A train of pulses of random starting phase is said to be

noncoherent. Its spectrum has the same shape as that of a

single pulse.

Coherence is a consistence or continuity in the phases of

successive pulses. Commonly, it is achieved by using a mas-

ter oscillator–power amplifier transmitter. The pulses are

then essentially cut out of a continuous wave.

The spectrum of a coherent pulse train of infinite length

consists of lines at intervals equal to the PRF, within an

envelope having the same shape as the spectrum of a single

pulse. If the coherent pulse train is not infinitely long, the

individual lines have a finite width and the same shape as

the spectrum of a single pulse the length of the train. Line

width is thus inversely proportional to the length of the

train.

Some Relationships To Keep In Mind

• For a single pulse:

Null-to-null bandwidth =

Where

τ = pulse width

• For a coherent pulse train

Line spacing = f

Null-to-null line width = =

Where f

= pulse repetition frequency

N = number of pulses in train

T = interpulse period

209

Mysteries of the Pulsed

Spectrum Unveiled

1. The spectrum of a signal is commonly portrayed as plot of

amplitude versus frequency.

n the preceding chapter, we became acquainted with

the dramatic effect that pulsed transmission has on

the spectrum of a radio wave. While it would suffice

merely to memorize the relationships summarized at

the end of that chapter, you will not only remember them

better but gain a deeper insight into the operation of a

radar if you understand the reasons for them.

This chapter gives the reasons. It begins by raising the

fundamental question of exactly what is meant by the

spectrum of a signal. This, as you’ll see, is actually the crux

of the matter. The chapter then explains the spectrum of a

pulsed signal in two quite different ways: first, in terms of

a conceptually simple but powerful analytical tool, called

the Fourier series,

and second, in terms of what physical-

ly takes place when a radio frequency signal passes

through a lossless narrowband filter. For those readers

who have some familiarity with calculus, the essence of

both explanations is presented in more precise, mathemat-

ical terms

–

the Fourier transform

–

at the end of the chapter.

Crux of the Matter

Much of the “mystery” which in many people’s minds

surrounds the spectrum of a pulsed signal stems from not

having a clear picture of what is meant by spectrum.

Spectrum Defined. Broadly speaking, the spectrum of a

signal is the distribution of the signal’s energy over the

range of possible frequencies. It is commonly portrayed as

a plot of amplitude versus frequency (Fig. 1).

In the last chapter, we gained a rough physical feel for

the spectrum of a pulsed signal by measuring the output

1. The series is named for

Jean Fourier, the 19th

century mathematician

and physicist who devel-

oped the concept.

PART IV Pulse Doppler Radar

210

that the signal produced when it was applied to a highly

selective receiver, tuned a hertz at a time through a broad

band of frequencies. Actually, you can define spectrum

quite rigorously in these terms, provided you refine them as

follows. Instead of envisioning the signal as being applied to

a receiver whose frequency is periodically changed, think of

it as being applied simultaneously to myriad lossless nar-

rowband filters whose frequencies are infinitesimally closely

spaced and cover the entire range from zero to infinity (Fig. 2).

A signal’s spectrum, then, is a plot of the amplitudes of the

filter outputs versus the frequencies of the filters.

By itself, this definition doesn’t clear up any of the “mys-

teries.” To explain them, we must in addition have a clear

picture of what a lossless narrowband filter actually does.

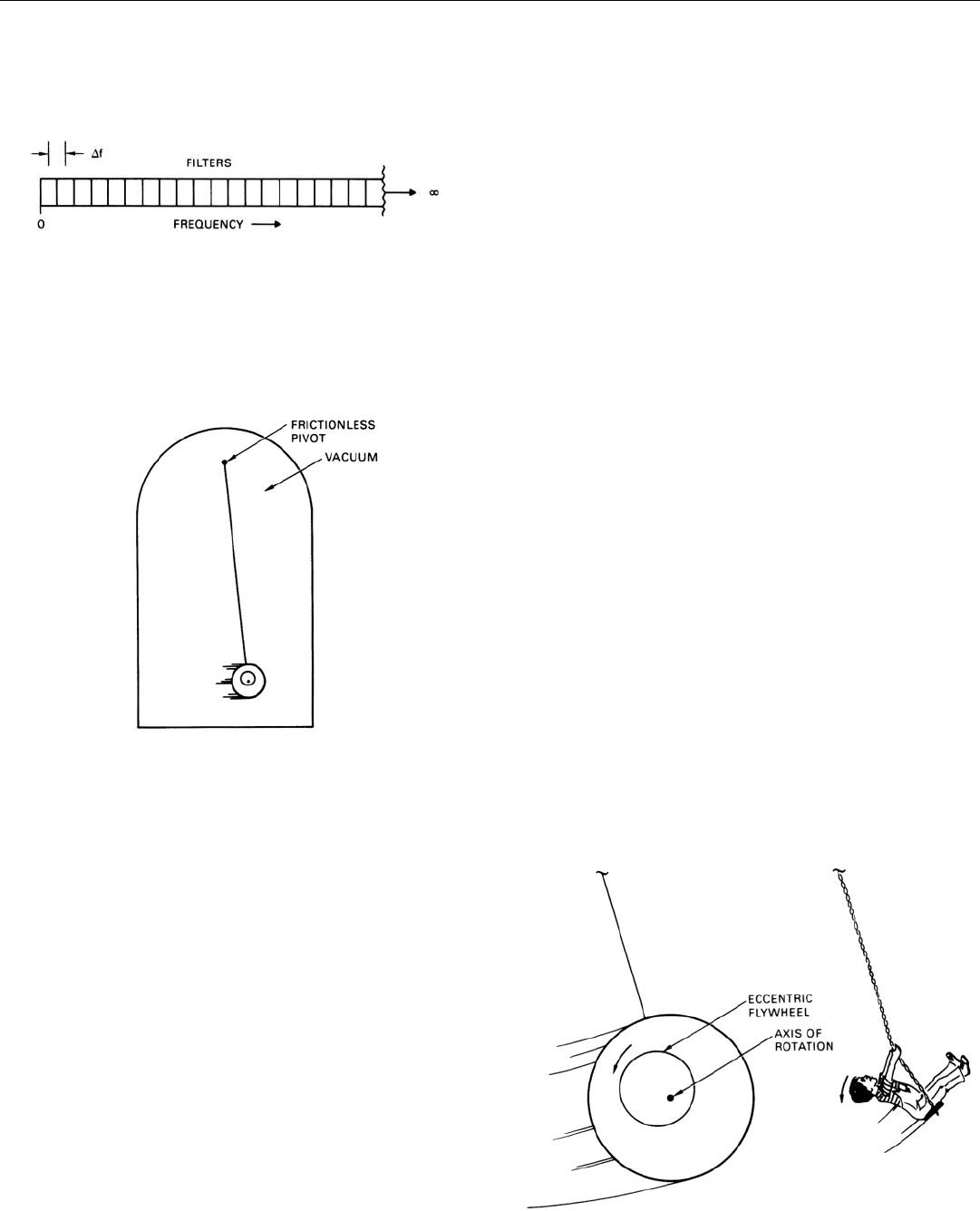
What a Lossless Narrowband Filter Does. The most

easily visualized mechanical analogy to a lossless narrow-

band filter is a pendulum suspended from a frictionless

pivot in a vacuum (Fig. 3).

The frequency of the filter is the pendulum’s natural fre-

quency—the number of cycles per second that it would

complete if deflected and allowed to swing freely.

The input signal is applied to the pendulum by a tiny

electric motor at the center of the pendulum mass. On the

shaft of this motor is an eccentric flywheel. The speed of

the motor is such that for every cycle of the input signal the

flywheel makes one complete revolution. Because of the fly-

wheel’s imbalance, a sinusoidally varying reactive force is

exerted on the pendulum.

This force tends to make the

pendulum swing alternately right and left. The effect is sim-

ilar to that of a child “pumping” a swing (Fig. 4).

The filter’s output is the amplitude to which the swing

builds up over the duration of the input signal.

2. To explain its spectrum, a signal may be envisioned as being

applied simultaneously to myriad lossless narrowband filters

whose frequencies are infinitesimally closely spaced.

3. A lossless narrowband filter is analogous to a pendulum sus-

pended from a frictionless pivot in a vacuum. Amplitude of

swing corresponds to filter’s output.

4. Motor driven eccentric flywheel makes one revolution for each

cycle of the input signal. Reactive force is similar to that produced

by a child “pumping” a swing.

2. To be completely rigorous,

besides plotting the amplitude

of each filter’s output, one

must also indicate its phase.

3. A more exact analogy is a

mass suspended on a spring,

since its restoring force is

directly proportional to the

displacement. But for small

displacements, the analogy to

a pendulum is very close.

By means of this analogy, it’s not too difficult to explain

why even the simplest ac signal has a broad frequency spec-

trum. Consider a signal that turns the flywheel at a rate of

1000 revolutions per second and has a duration of 1/10th

second. To see what its spectrum is like, we apply the signal

simultaneously to our myriad filters. As the flywheels start

turning, all of the pendulums begin to swing. The extent to

which each pendulum’s swing builds up, however, depends

upon the pendulum’s natural frequency.

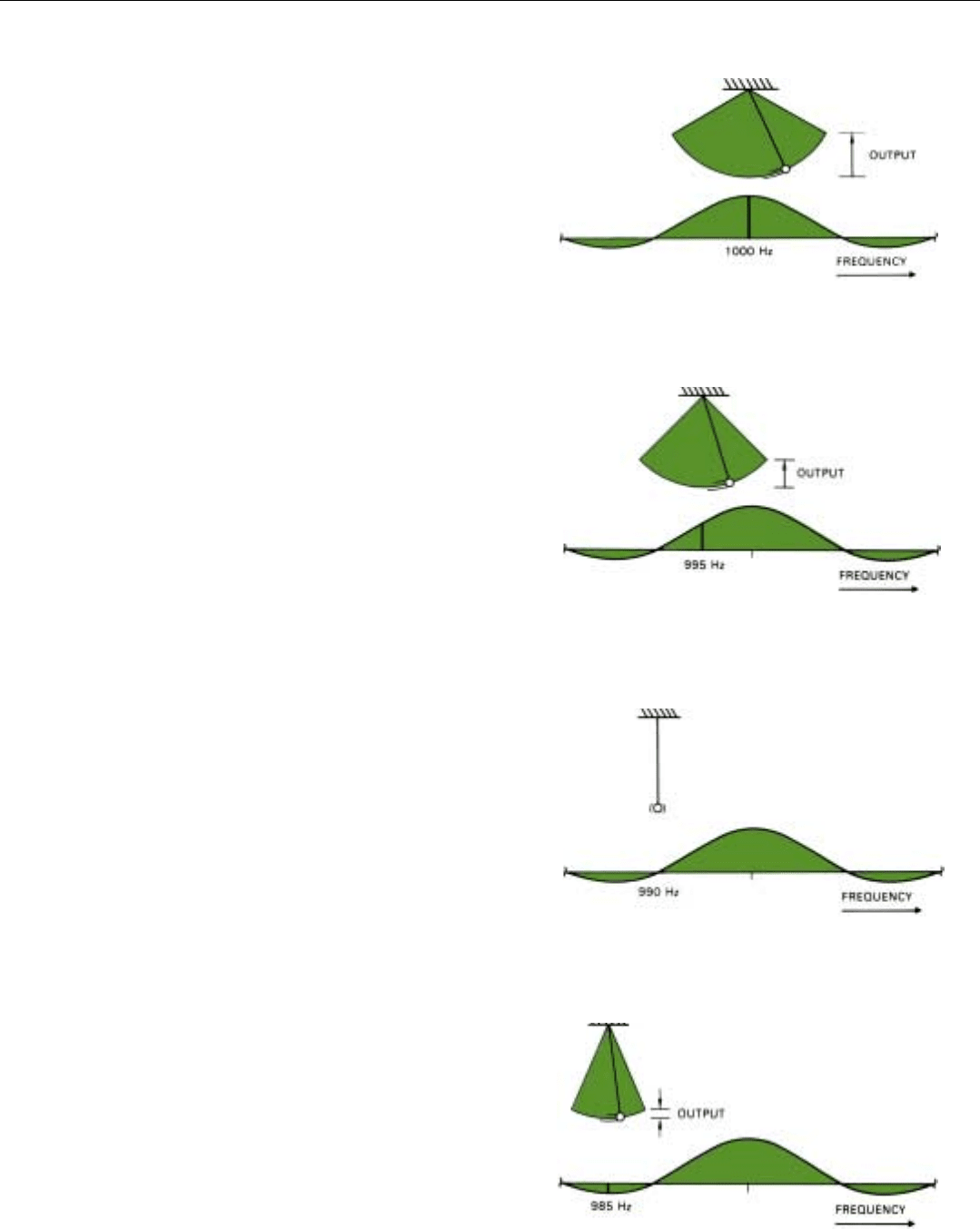
In the case of the pendulum whose frequency is exactly

1000 hertz (Fig. 5), with every turn of the flywheel, the

amplitude of the swing increases by the same amount. The

swing remains in phase with the sinusoidally varying forces

exerted by the flywheel. After 1/10th of a second has

elapsed and the flywheel has made 100 turns, the pendu-

lum is swinging with an amplitude 100 times as great as

when the input completed its first cycle.

In the case of a pendulum whose frequency is, say, 5

hertz less than 1000 (Fig. 6), the swing starts building up

in the same way. But because of the pendulum’s lower nat-

ural frequency, the phase of the swing gradually falls behind

that of the flywheel’s rotation. Consequently, the momen-

tum of the pendulum and the reactive forces of the flywheel

work against each other over a correspondingly increasing

fraction of each cycle. When the input stops, the amplitude

of this pendulum’s swing is considerably less than that of

the pendulum whose frequency is 1000 hertz. Neverthe-

less, the swing is substantial.

But in the case of the pendulum whose frequency is 10

hertz less than 1000 (i.e., the frequency of the input signal’s

first spectral null), the phase of the swing falls behind at a

high enough rate that the swing is completely damped out

by the time the input ends (Fig. 7).

However, for the pendulum whose frequency is 15 hertz

less than 1000 (i.e., in the middle of the first sidelobe), the

phase of the swing falls behind at a sufficiently high rate

that the swing builds up and damps out and builds up once

again before the input ends. Though the final amplitude of

the swing is only a fraction of that of the pendulum whose

frequency is 1000 hertz, this fraction is considerable—

roughly 21 percent (Fig. 8).

Moving on to pendulums whose frequencies are farther

and farther below 1000 hertz, we observe the familiar pat-

tern of lobes and nulls. At corresponding points within suc-

cessive lobes, the farther the lobe is from 1000 hertz, the

more nearly the total time during which pendulum and fly-

wheel work against each other equals the total time during

which they work together. Hence, the less the final ampli-

tude of the pendulum’s swing is. But no matter how far

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

211

5. Swing of pendulum whose frequency is 1000 hertz stays in

phase with reactive force of flywheel and builds up.

6. Momentum of pendulum whose frequencyis 995 hertz works

against flywheel part of the time, so buildup is not as great.

7. Swing of pendulum whose frequency is 990 hertz builds up

initially, but is completely damped out when signal ends.

8. Swing of pendulum whose frequency is 985 hertz falls behind

sufficiently fast that it builds up again before input ends.

PART IV Pulse Doppler Radar

212

down in frequency we go, only at those frequencies for

which the periods of buildup and damping are exactly equal

is a pendulum completely at rest when the input ends.

For the pendulums whose frequencies are greater than

1000 hertz, the responses are similar.

Thus, the spectrum of every signal we encounter covers

an immensely broad band of frequencies. True, the energy

at most of these frequencies is minuscule. But the shorter

the signal, the more widely its energy is spread. For exam-

ple, if we reduce the duration of the signal we have been

considering by a factor of 10, when the input ends, the shift

in phase of each pendulum’s swing will be only 1/10th as

great as before.

So the nulls on either side of the signal’s central spectral

lobe will be 10 times farther apart than they were (Fig. 9)

and the distribution of the signal’s energy will be propor-

tionately broader.

Following this general line of reasoning, a far less cum-

bersome graphic model of a lossless filter may be used.

With it, later in this chapter, we will analytically deduce all

of the results of the experiments of Chap. 16, practically in

our heads.

At this point, though, one thing more should be said

about narrowband filters. A lossless filter differs from most

of the filters with which we are familiar in two important

respects.

First, whereas the output of a conventional analog filter

builds up fairly quickly to a “steady-state” value when a

constant-amplitude input of the filter’s frequency is applied,

the output of a lossless filter continues to build up as long as

the input continues (Fig. 10).

Second, whereas the output of a conventional filter

decays after the input stops, the output of a lossless filter

retains its last value for an unlimited time, unless the out-

put is dumped in some way.

In short, a lossless filter can be thought of as efficiently

integrating the energy of that component of the input signal

which has the same frequency as the filter.

That’s all very well, you may say. But how can a purely

sinusoidal signal which completes a given number of cycles

per second really have a component of energy at any other

frequency? The fact is, it does. To see why, though, we must

look a little more closely at the definition of frequency.

Definition of “Frequency.” As defined in Chap. 4, the

frequency of a sinusoidal signal is indeed the number of

cycles the signal completes per second. But that definition,

you may recall, was qualified as applying strictly to a con-

tinuous, unmodulated signal.

9. Complete spectrum of 1/10 second pulse discussed in the text

(top). Although most of the energy is centered around the car-

rier frequency (1000 hertz), if the pulse’s duration is

decreased to 1/100 second (bottom), the central spectral

lobe alone spreads over a band 200 hertz wide.

10. Difference between outputs of a lossless filter and a conven-

tional analog filter. Lossless filter is a perfect integrator.

Click for high-quality image