George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

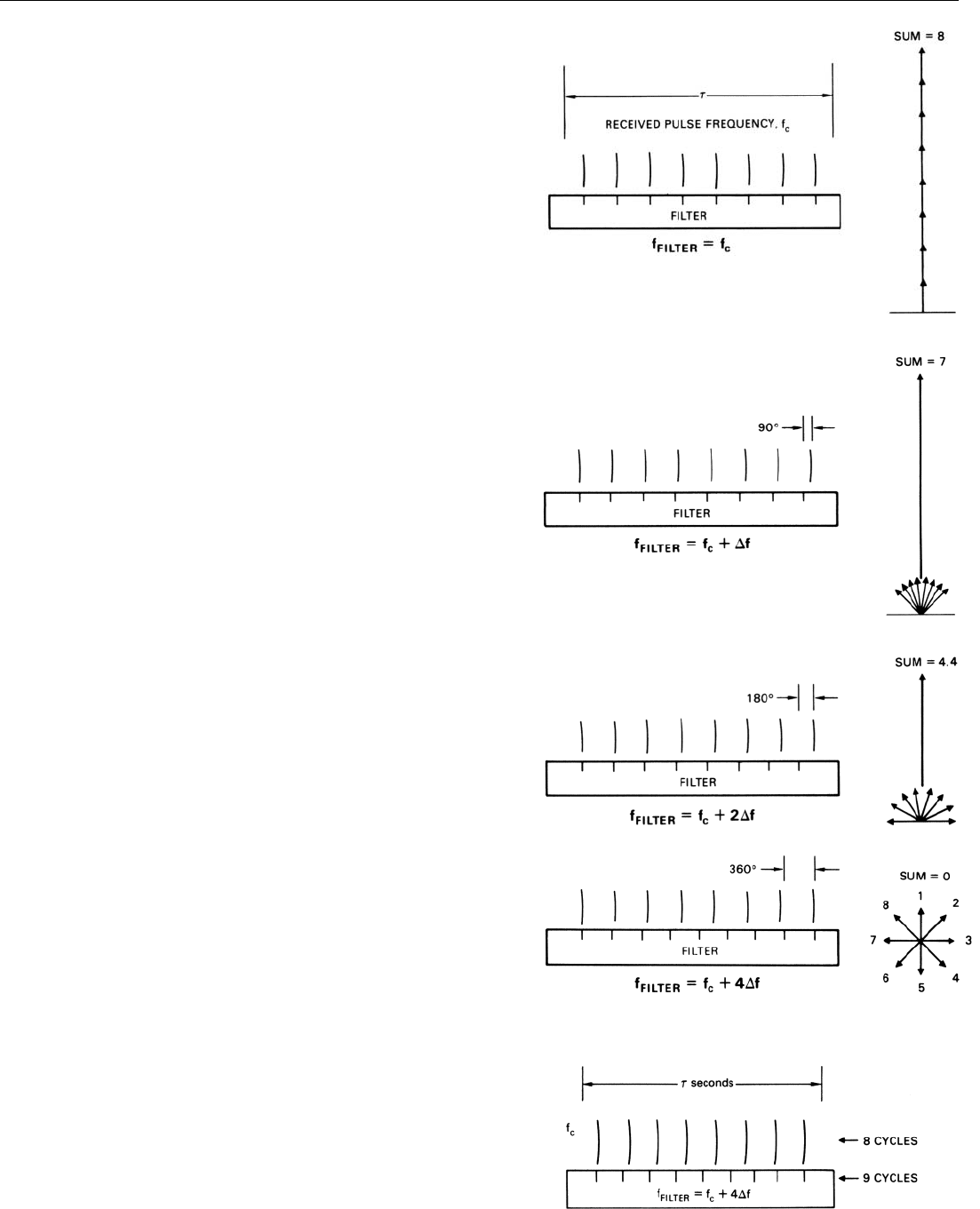
the same direction—i.e., the cycles they represent have the

same phase—the sum will be n times the length of the pha-

sors. If they point in slightly different directions, the sum

will be less. And if they point in opposite directions—i.e.,

the cycles are 180° out of phase—they will cancel.

With this simple analogy in mind, let us analyze the

results of some of the experiments performed in the preced-

ing chapter.

Spectrum of a Single Pulse. To see why the spectrum of

a single pulse is continuous over a band of frequencies 2/τ

hertz wide, we measure a pulse τ seconds long with four

different rulers. Each ruler represents a narrowband filter

tuned to a different frequency.

In Fig. 26(a), the filter has the same frequency as the

pulse’s carrier (f

). Consequently, the phases of the wave

crests relative to the marks on the ruler are all the same.

The phasors representing the individual cycles of the wave

all point in the same direction. The pulse is eight cycles

long. Assuming that the length of each phasor is one, their

sum is eight.

In Fig. 26(b) the same pulse is applied to a filter having a

higher frequency (f

+ ∆f); the wavelength marks are closer

together. As a result, there is a progressive shift in the phas-

es of the wave crests relative to the marks. Over the length

of the pulse, the shift builds up to a quarter of a wave-

length. The phasors, therefore, fan out over 90°. Even so,

their sum is nearly seven.

In Fig. 26(c), the filter has a considerably higher frequen-

cy (f

+ 2∆f). The total accumulated phase shift over the

length of the pulse now is half a wavelength (180°). Still,

the sum is nearly half what it was for the filter tuned to f

In Fig. 26(d), the filter has a sufficiently high frequency

+ 4∆f) that the phase shift over the length of the pulse is

one whole wavelength. As a result, the phasors are uni-

formly spread over 360°. Pointing in opposite directions,

the phasors for cycles No. 1 and No. 5 cancel. So do the

phasors for cycles No. 2 and No. 6, No. 3 and No. 7, and

No. 4 and No. 8. The pulse produces no output from the

filter; we have reached a frequency where there is a null in

the pulse’s spectrum.

What is this frequency? Over the duration of the pulse

the oscillation of the filter that was tuned to the null fre-

quency completed one more cycle than the pulse’s carrier

(Fig. 27). The duration of the pulse was τ seconds. So, the

filter’s frequency was 1/τ cycles per second (hertz) higher

than the carrier frequency, f

. The null frequency, therefore,

is (f

+1/τ).

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

223

26. If a filter is tuned to progressively higher frequencies, the

cumulative phase shift over the length of a pulse increases.

27. At null, in τ seconds filter completes one more cycle than signal.

(a)

(b)

(c)

(d)

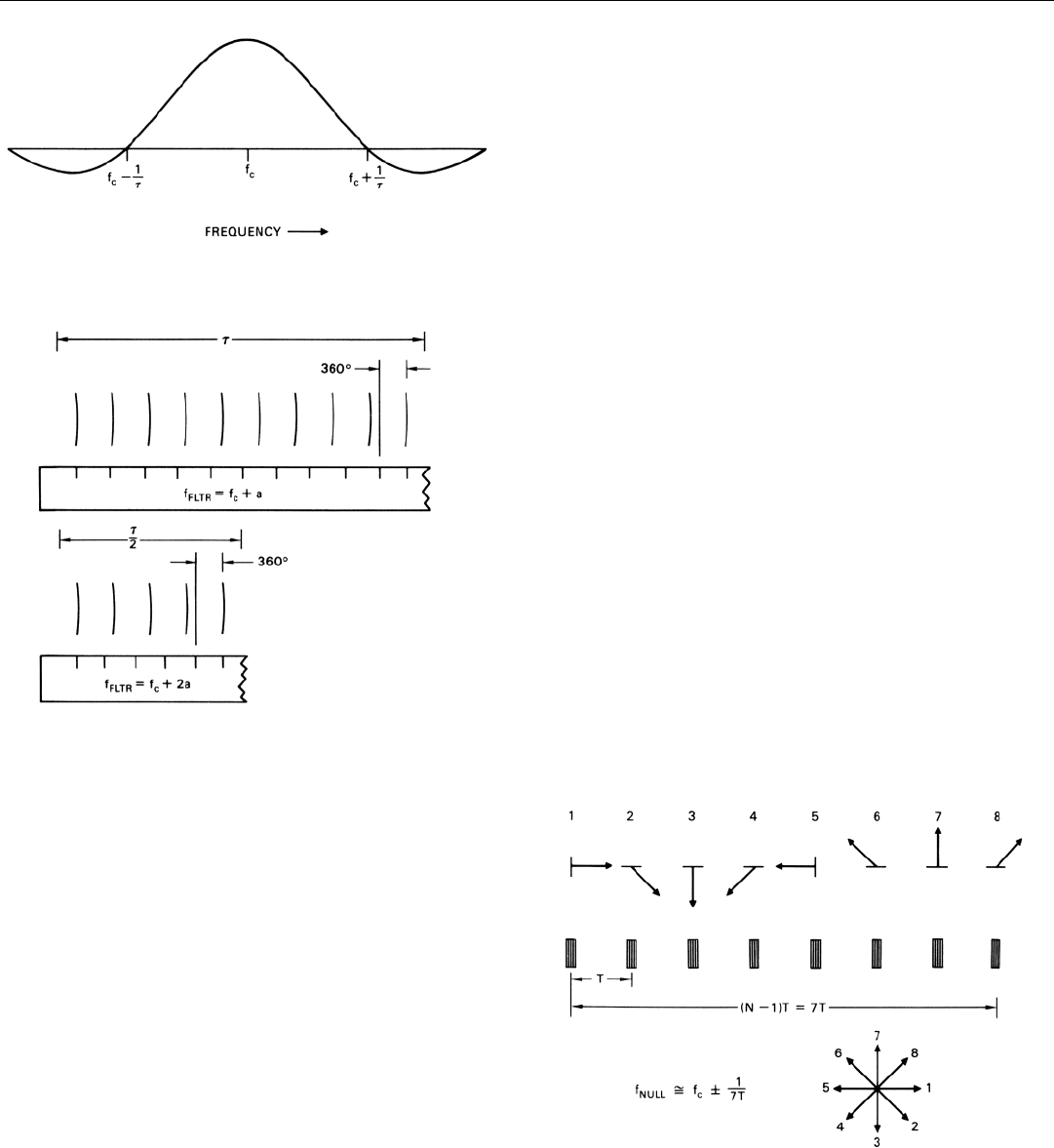
PART IV Pulse Doppler Radar

224

28. A plot of the phasor sums has a sin x/x shape with nulls 1/τ

hertz above and below the carrier frequency, f

29. The shorter a pulse is, the greater the frequency difference

must be to produce a 360° phase shift over the length of the

pulse.

Following the same line of reasoning, we similarly find a

null 1/τ cycles per second below f

(Fig. 28). The null-to-

null bandwidth of a single pulse, therefore, is 2/τ hertz—

exactly as was observed in Experiment No. 2 of Chap. 16.

Upon a little reflection, the fundamental reason for the

filter’s response become clear. A difference in frequency is

actually a continuous linear shift in phase. When a pulsed

signal is applied to a filter, the rate of this shift in cycles per

second equals the difference between the signal’s carrier fre-

quency and the frequency of the filter. In the case of a sin-

gle pulse, only when this difference is large enough to make

the total phase shift over the duration of the pulse equal

one whole wavelength, do the individual cycles of the

received wave entirely cancel. The shorter the pulse

(Fig. 29), the greater the frequency difference must be to

satisfy this condition. Conversely, the longer the pulse, the

less the frequency difference must be. Thus, for a pulse

whose duration is 1 microsecond, the null-to-null width of

the central spectral lobe is 2 ÷ 10

-6

= 2 MHz. For a pulse

whose duration is 1 second, the spectral line width is 2

hertz. And for a pulse whose duration is 1 hour, the spec-

tral line width is only 2 ÷ (60 x 60) ≅ 0.00056 Hz.

Spectrum of a Coherent Pulse Train. To see why the

null-to-null width of the central spectral lobe is drastically

reduced when the filter integrates a train of coherent pulses,

we represent each pulse with a single phasor (Fig. 30).

The nulls now occur when the total phase shift over the

length of the pulse train is one wavelength. Since the train

is many times longer than a single pulse, the frequency dif-

ference that produces a phase shift of one wavelength is

many times smaller for the train than for a single pulse.

30. The amplitude and phase of each pulse in a train may be rep-

resented by a phasor. Spectral nulls occur when phase shift

over length of train is 360°.

Take a train of 32 pulses, for example (Fig. 31). Suppose

the interpulse period is 100 times the pulse width. The

duration of the train, then, will be roughly 31 x 100 =

3100 times the duration of a single pulse, making the null-

to-null bandwidth of the line only 1/3100 that of a single

pulse.

It is instructive to consider the effect of deleting every

other pulse in this train. Because the length of the pulse

train is essentially the same, the phasors for the remaining

16 pulses would still cancel at almost the same frequency;

so the null-to-null bandwidth would be about the same.

Since there would be only half as many pulses, however,

the amplitude of the filter output would be only half as

great. Finally, since the PRF would be only half as great,

the pulses would produce an output from the filter at

twice as many points within the envelope established by

the pulse width. How do we explain why the pulse train

produces an output at intervals equal to the PRF in the

first place?

Repetition of Spectral Lines. As we have seen, when a

train of pulses is applied to a filter, what causes the output

of the filter to fall off as the filter is tuned away from the

carrier frequency of the pulses is the pulse-to-pulse differ-

ence in the phase of the carrier, as seen by the filter. But,

since phase angles are repeated every 360°, there is no way

of telling whether the phase of any one pulse is the same as

that of the preceding pulse or has been shifted by some

multiple of 360°.

A pulse-to-pulse shift of 360° amounts to one cycle per

interpulse period, corresponding to an increment of fre-

quency equal to the PRF (Fig. 32). Consequently, there may

be very little difference between a filter’s response to a pulse

train whose carrier frequency is the same as the filter fre-

quency and its response to a pulse train whose carrier fre-

quency is some integer multiple of the PRF above or below

the filter frequency. In fact, the only difference is that due to

the phase shift occurring from cycle to cycle over the dura-

tion of each pulse. Unless the multiple of the PRF is very

high or the pulse width is a fairly large fraction of the inter-

pulse period—i.e., unless the carrier frequency is near one

end or the other of the envelope established by the pulse

width—the difference is slight.

Mathematical Explanation of the Pulsed Spectrum

For those having at least a nodding acquaintance with

calculus, the spectrum of a pulsed signal is derived math-

ematically in the following panel. If your interest is not so

mathematical, then skip ahead to “Results” on page 230.

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

225

31. If every other pulse in a train is deleted, the output is reduced,

but the bandwidth remains essentially unchanged.

32. Pulse trains whose carrier frequencies equal the filter frequen-

cy, f

, (top) and f

plus the PRF (bottom). Only difference in

the outputs produced by the two trains is that due to the cycle-

to-cycle phase shift within each pulse of the second train.

5. Although the train contains

32 pulses, it is only one pulse

width longer than 31 inter-

pulse periods.

PART IV Pulse Doppler Radar

226

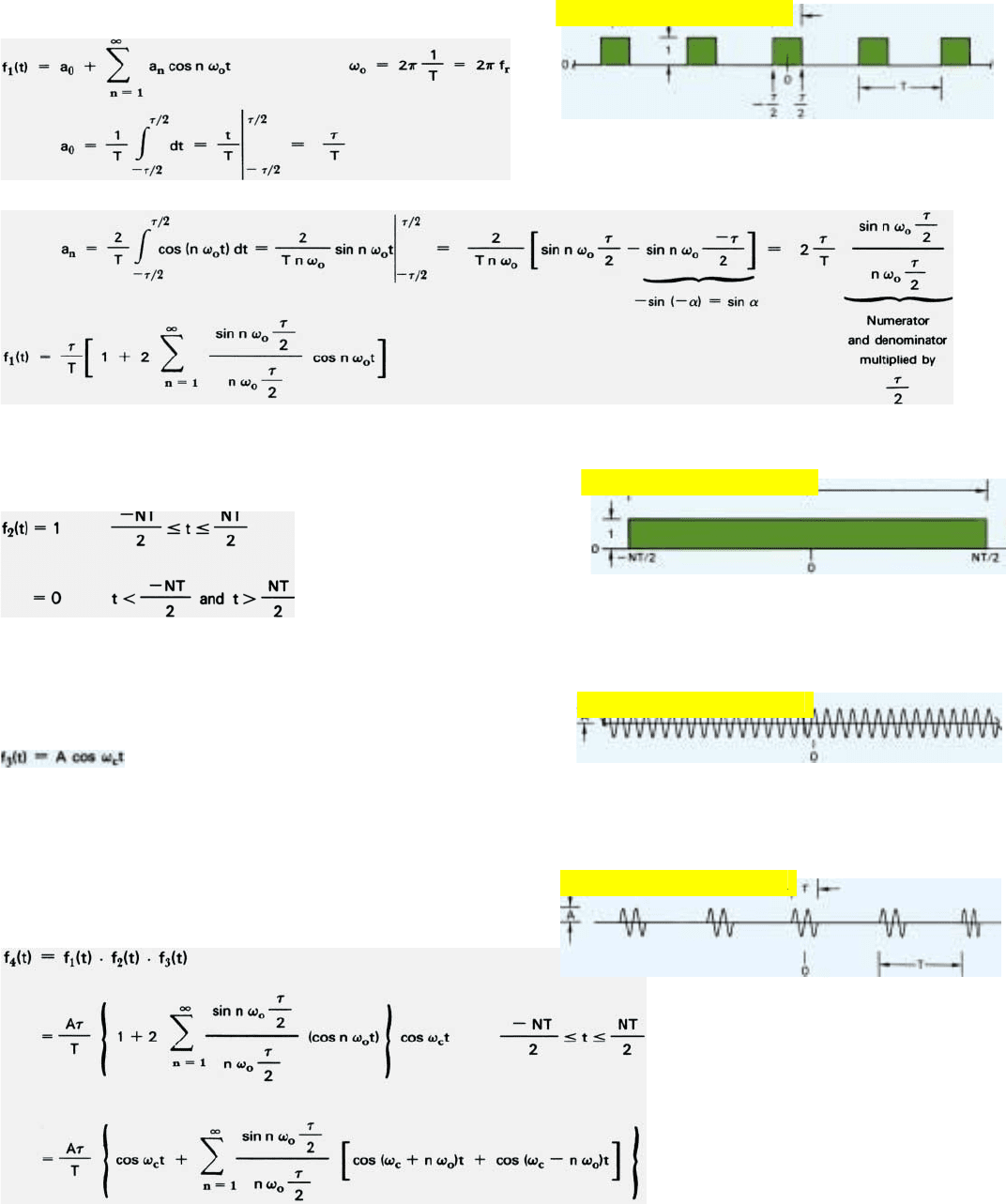
General Approach. Basically, the panel shows two things:

first, the derivation of a mathematical expression for a pulse

modulated carrier signal as a function of time, f(t), and second

the transformation of this expression from the time domain to the

frequency domain —in other words, the derivation of the Fourier

transform for the signal.

The expression for the pulse modulated signal is derived by

writing separate expressions for each of the following.

• An infinitely long pulsed video signal, f

(t), having an

amplitude of 1, a pulse width τ, an interpulse period T, and

a pulse repetition frequency (expressed in radians per

second) of ω

where (ω

= 2π/T = 2πf

MATHEMATICAL EXPLANATION OF THE PULSED SPECTRUM

In the text, the spectrum of a pulsed signal is explained in

several quite different nonmathematical ways, at least one of

which is a bit unconventional. While hopefully these explanations

have provided some helpful insights, the spectrum can be

explained much more rigorously

and

succinctly in purely

mathematical terms.

Accordingly, a mathematical derivation of the spectrum of a

simple, perfectly rectangular pulsed signal is presented on the

third and fourth pages of this panel.

In case your math is a little rusty, a brief preliminary explanation

of the derivation is given on this and the facing page.

• A signal, f

(t), having an amplitude of 1 and a duration equal to

the length of a train of N pulses whose interpulse period is T.

• An infinitely long carrier wave, f

(t), having an amplitude A,

and a frequency expressed in radians per second of ω

where (ω

= 2πf

The expression for the pulsed video signal, f

(t), is obtainedby evalu-

ating the coefficients (a

, a

. . .)* of the Fourier series in terms of

the pulse width,



, and interpulse period, T, of the signal and substi-

tuting these values into the series.

Multiplying the first two functions, f

(t) and f

(t), together gives an

equation for the pulsed modulating signal. Multiplying the function for

the carrier wave, f

(t), by this product yields th desired equation for

the pulse modulated carrier, f

(t).

The Fourier transform of this function is then derived, yielding the

spectrum of the pulse modulated signal. The essense of both deriva-

tions is briefly outlined on the next page.

By positioning zero on the time axis

in the center of one of the pulses, the

coefficients of the sine terms are reduced

to zero. (The signal has even symmetry.)

Click for high-quality image

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

227

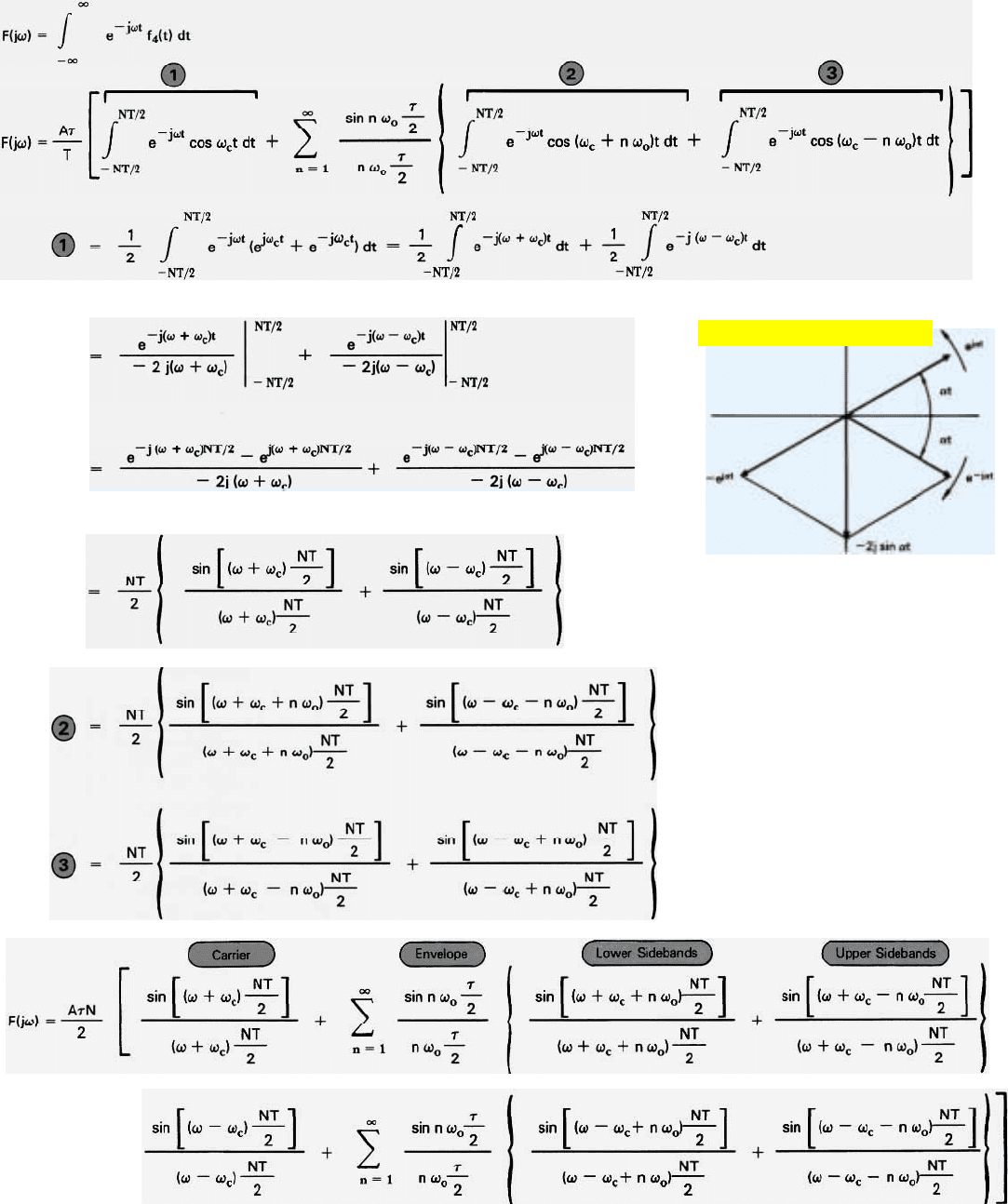
Essence of the Derivations. In evaulating the coefficients of

the Fourier series for the pulsed video signal, the key operation is

multiplying the equation for the signal by cos ωt for the frequency

of the harmonic whose coefficient we wish to obtain. As illustrated

in the figure below, when the instantaneous amplitudes of two sine

waves of the same phase and frequency are multiplied together,

their product is positive for both halves of every cycle. (The same

is true of cosine waves.)

Consequently, if the product is integrated over a complete cycle,

the result divided by the period of the cycle is one-half the product

of the peak amplitudes of the two waves. If the amplitude of one of

the waves is one, then the product is one-half the peak amplitude

of the other wave.

Yet, if the frequencies of the two waves are not the same, the

sign of the product will alternate between (  ) and (  ). If the

frequency of one wave is an integer multiple of the frequency of

the other, when the product is integrated over the period of the

lower frequency wave, the result will be zero.

Thus, the coefficients of the Fourier series for our continuously

repeating pulsed video signal can be found by multiplying the

mathematical expression for the waveform by the cosines of ω

2ω

t, 3ω

t, . . . nω

t, in turn, integrating each product over the

waveform’s repetition period, T, and dividing by T/2. The dc

coefficient (average amplitude) is found by integrating the

expression for the wave alone over the period T and dividing by T.

Similarly, in deriving the Fourier transform, that component of the

pulse modulated wave having a particular frequency, ω, can be

found by multiplying the equation for the wave (as a function of time)

by cos ωt



j sin ωt and integrating the product. In this case, since

ω is not necessarily an integer multiple of the fundamental of the

modulated wave, the product must be integrated over the entire

duration of the pulse train, i.e., from



NT/2 to



NT/2. As with the

Fourier series, the dc component is found by integrating the expres-

sion for the wave alone over the same period and dividing by its

duration.

In deriving the Fourier transform, the sinusoidal functions are

expressed most conveniently in exponential form. The relationships

between the two forms were explained with phasors in Chapter 5

and are summarized in the diagram below.

The only calculus you need to know to follow the derivation is that

the integral of the cosine of ~t is 1/w times the sine of ~t and the

integral of e

j



1/jω times e

j

One other reminder. If a quantity raised to a given power is

multiplied by the same quantity raised to another power, the

product is the quantity raised to the sum of the two powers. Thus,

With the above relationships in mind, let us proceed with the

derivations. The expression for the pulse modulated carrier is

derived on the next page; the Fourier transform of this expression,

on the facing page.

Click for high-quality image

PART IV Pulse Doppler Radar

228

MATHEMATICAL EXPLANATION OF THE PULSED SPECTRUM (Cont’d.)

1. Continuous Pulsed Modulation Signal (Expressed as a Fourier Series)

2. Duration Pulse Modulation

3. Unmodulated Carrier

4. Pulse Modulated Carrier (Product of expressions 1, 2, and 3)

Click for high-quality image

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

229

5. Fourier Transform of Pulse Modulated Carrier

Click for high-quality image

PART IV Pulse Doppler Radar

230

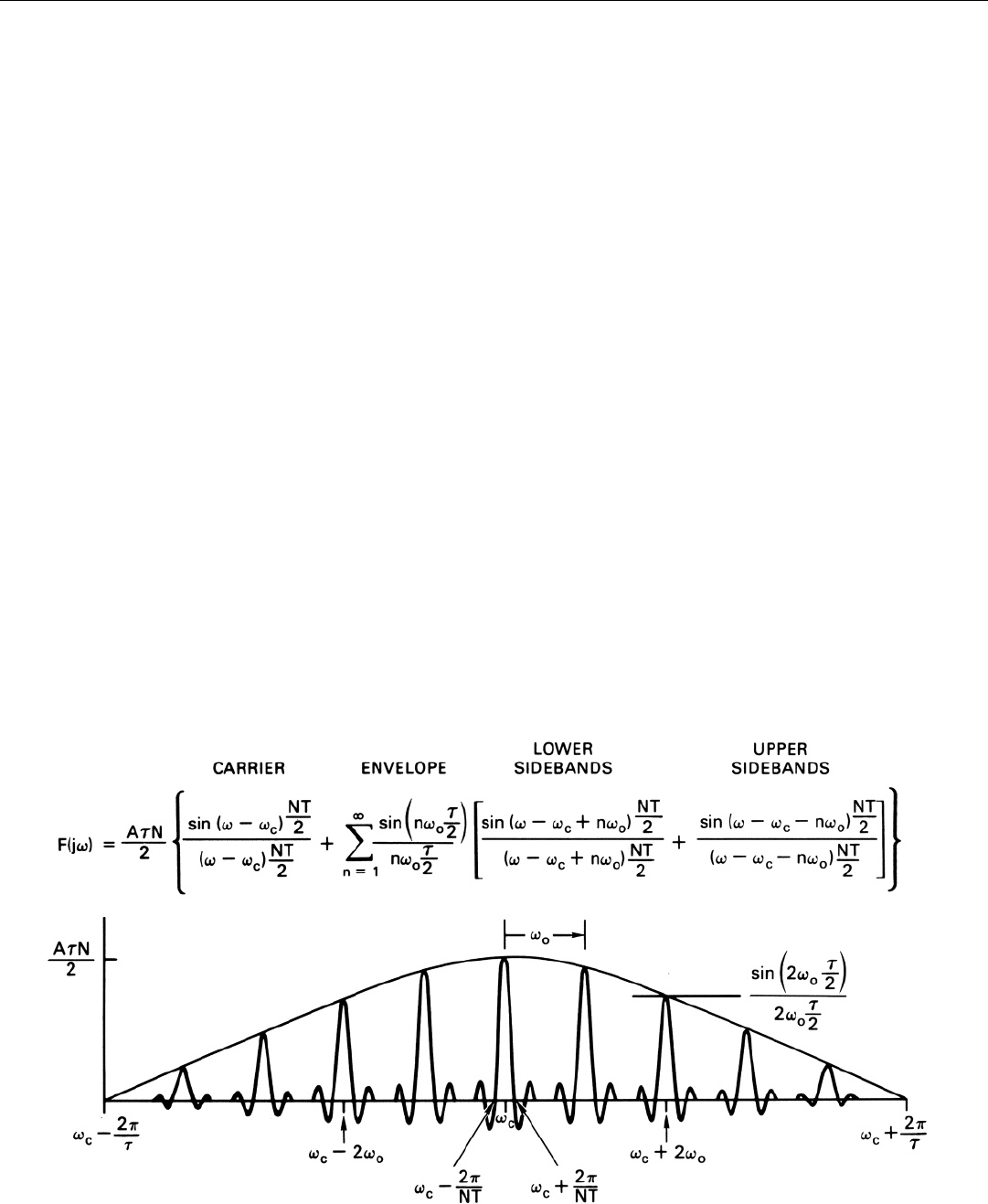
Results. The final equation obtained in the panel on

preceeding page is the Fourier transform for a train of N

perfectly rectangular pulses having these characteristics:

• Carrier frequency, ω

= 2πf

• Pulse width, τ

• PRF, ω

= 2πf

• Interpulse period, T

• Duration, NT

The transform consists of two similar sets of terms. The first

set applies to frequencies having negative values; the sec-

ond set, to frequencies having positive values.

So we can examine it more easily, the positive-frequency

portion of the transform is repeated in Fig. 33. The first

term inside the braces represents the spectrum of the cen-

tral spectral line—the carrier. Immediately following the

summation sign is the sin x/x term giving the envelope

within which the other spectral lines fit. The remaining

terms represent the lines above and below the carrier.

By substituting appropriate values for N (number of

pulses), one can apply this same equation to pulse trains of

virtually any length.

Beneath the equation is a plot of the spectrum—ampli-

tude versus frequency in radians per second—obtained by

33. Positive-frequency portion of the Fourier transform for a rectangular train of N pulses. The pulses have a width τ, a carrier frequency of ω

, a

PRF of ω

, and an interpulse period of T.

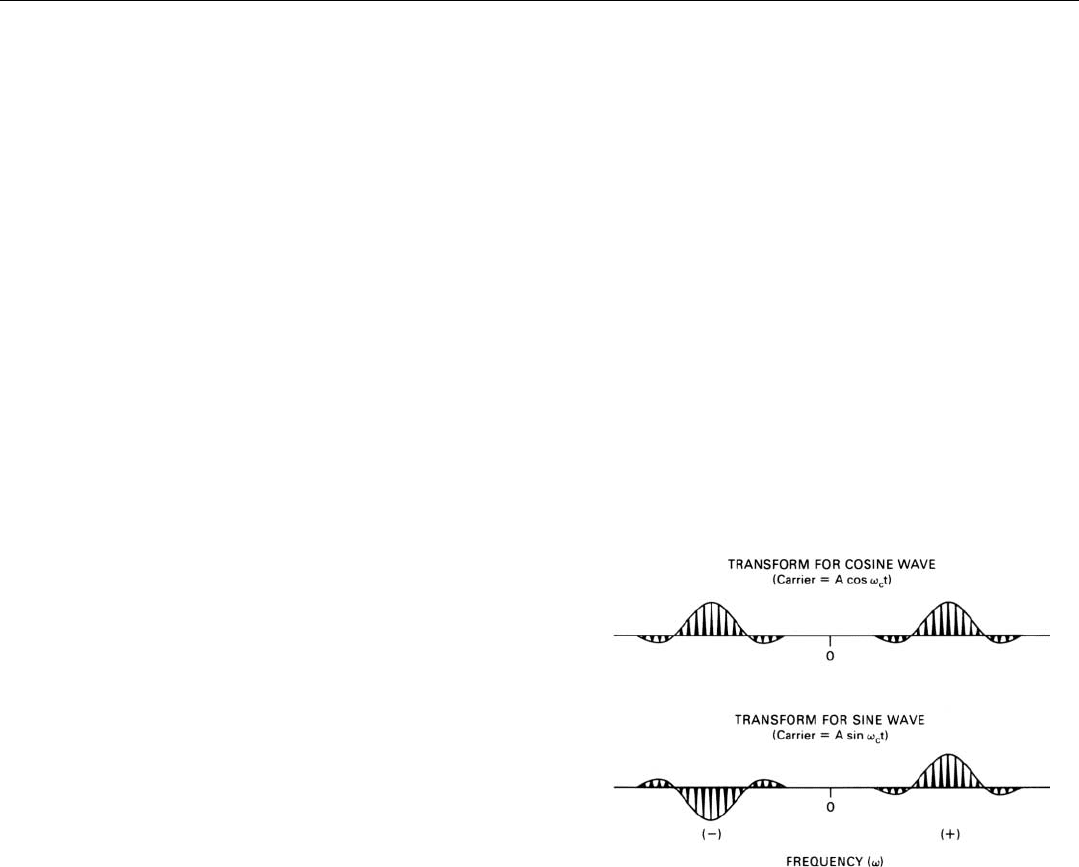
evaluating the equation for values of ω covering a wide

enough range of positive frequencies to include the entire

central lobe of the envelope. The first pair of nulls in the

envelope occurs 2π/τ radians per second above and below

the carrier frequency ω

. Within the envelope, spectral lines

occur above and below the carrier frequency, at intervals

equal to the PRF, ω

. Each line has a sin x/x shape, with

nulls 2π/NT above and below the line’s central frequency.

Needless to say, these results are identical with those

deduced earlier in the chapter, first, with the aid of the

Fourier series and, second, simply with phasors. Hopefully,

one or another of these explanations has removed the veil

of mystery (if indeed there was one) from the spectrum of

the pulsed signal.

Significance of the Negative-Frequency Terms. Many

people are puzzled by the negative-frequency components

of the Fourier transform. Yet they needn’t be.

It so happens that these components are what reflect the

difference between the transform for a signal whose carrier

is a cosine wave and the transform for a signal whose carri-

er is a sine wave. In the case of the transform for a cosine

wave (Fig. 34A), such as the one we just derived (carrier is

A cos ω

t), the algebraic signs of the negative-frequency

terms are the same as the signs of the corresponding posi-

tive-frequency terms. Whereas, in the case of the transform

for a sine wave (carrier is A sin ω

t), the signs of the nega-

tive-frequency terms (Fig. 34B) are the opposites of the

signs of the corresponding positive-frequency terms.

If the signal is considered alone, the negative-frequency

terms have no significance—i.e., contribute no additional

information regarding what frequencies are present. Since

cos (–ωt) = cos ωt, the energy represented by the negative-

frequency terms of the transform for a cosine wave merely

adds to the energy represented by the corresponding posi-

tive-frequency terms. And since sin (–ωt) = –sin ωt, the

energy represented by the negative-frequency terms of the

transform for a sine wave likewise merely adds to the ener-

gy represented by the positive frequency terms.

However, in the case of a signal that has been resolved

into I and Q components (see Chap. 5, page 67), the nega-

tive-frequency terms do contribute additional information.

As we shall see in Chap. 19, when the signal is translated to

the video range, the signal’s Fourier transform will have

only negative-frequency terms if the frequency of the origi-

nal signal was lower than that of the reference signal used

in the frequency translation. And the transform will have

only positive-frequency terms if the frequency of the origi-

nal signal was higher.

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

231

34. Comparison of frequency spectra for a signal whose carrier

is a cosine wave and a signal whose carrier is a sine wave.

Note that the algebraic signs of the negative frequency terms

are reversed for the sine wave.

PART IV Pulse Doppler Radar

232

What the Amplitudes Represent. One important ques-

tion, though, remains to be answered. All of the spectra

shown thus far have been plots of amplitude versus fre-

quency. But nothing has been said about how this ampli-

tude relates to the amplitude of the wave in the time

domain, or even what units it is expressed in.

We can clear up this deficiency by examining the first

term of the Fourier transform—the term which establishes

the peak amplitude of the envelope

AτN

The factor, A, you may recall, was defined in the panel as

the peak amplitude of the carrier wave. Assuming that A is

a voltage, then the spectrum is a plot of voltage versus fre-

quency.

Going a step further, since power is proportional to volt-

age squared, by squaring the values of amplitude given by

the Fourier transform, we can obtain the power spectrum of

the pulsed signal (Fig. 35).

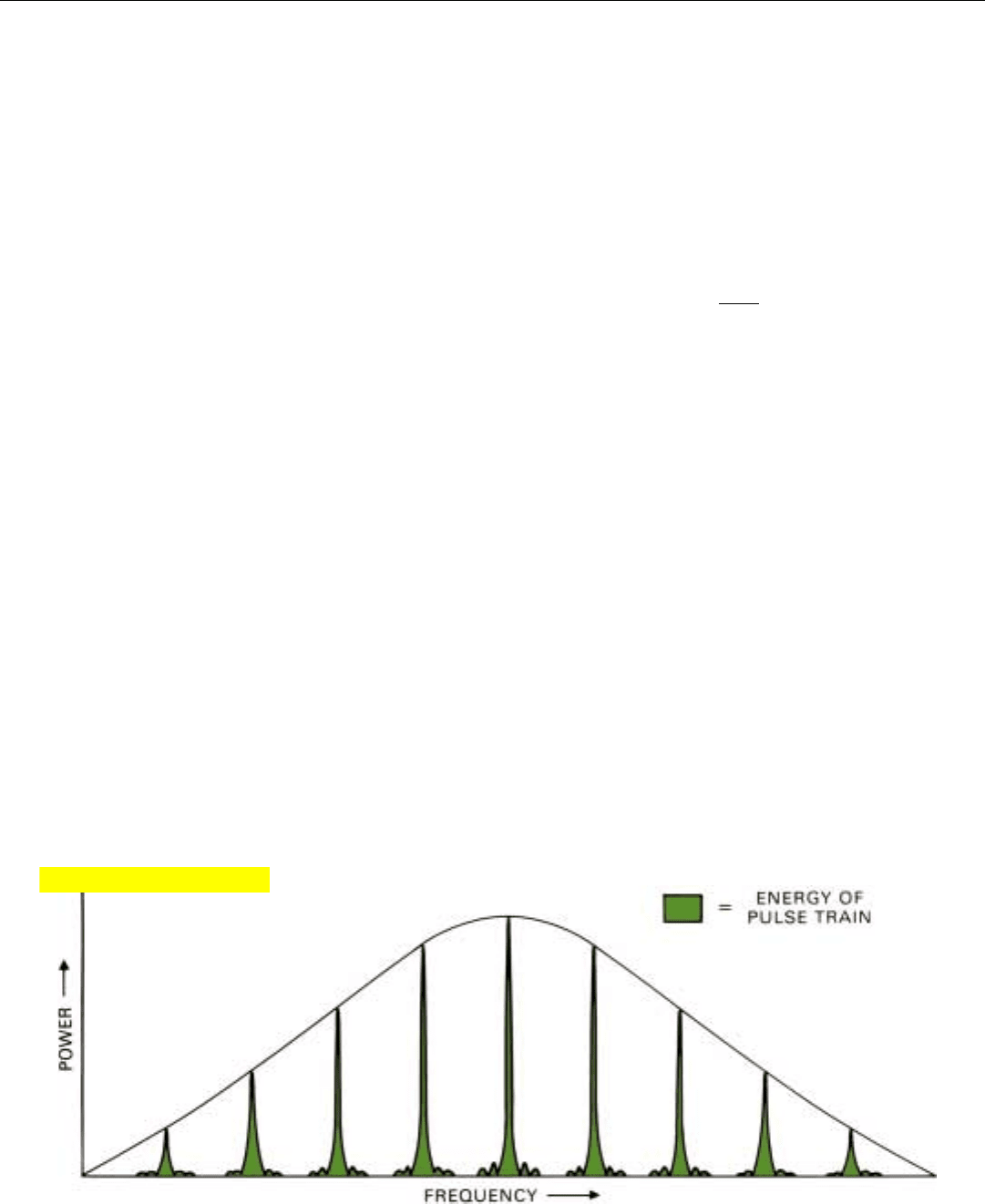
Energy, of course, is power times time. It can be shown

mathematically

that the total area under the power spec-

trum equals the total energy of the pulsed signal. The power

spectrum thus illustrates how the energy of the signal is dis-

tributed in frequency. For example, by measuring the area

encompassed by the central line of the power spectrum and

dividing it by the total area encompassed by the spectrum,

we can tell what fraction of the signal’s energy is contained

in that line.

35. If the amplitude represented by a signal’s Fourier transform is a voltage, then a plot of the amplitude squared versus frequency is the signal’s

power spectrum, and the area under this plot corresponds to the signal’s energy.

6. Parseval’s formula.

Click for high-quality image